Rep:Mod:twpphysical
Cope Rearrangement Tutorial
Introduction
 |
The Cope rearrangement of 1,5-hexadiene, a [3,3]-sigmatropic shift, has been the subject of many experimental and computational studies. The mechanism was the subject of debate for a long time although it is now accepted that it proceeds in a concerted fashion via a chair or boat transition structure. The boat transition structure is higher in energy than the chair transition structure. In this report, the transition structures will be found and studied using Gaussian.
Optimizing the Reactants and Products of Cope Rearrangement
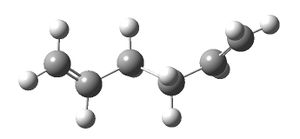
The antiperiplanar conformation of 1,5-hexadiene was drawn GaussView and the structure was cleaned up. Optimisation was performed at the H-F/3-21G level to give a total energy of -231.69260237 Hartrees and a C2 point group.
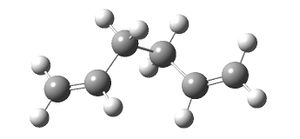
The gauche conformation was drawn and optimised at the same level to give a total energy of -231.69266120 Hartrees and a C1 point group.
The gauche conformation is the more stable than the antiperiplanar conformation as it is 0.0000588 Hartrees (0.154 kJ mol-1) lower in energy. This is because there is a stabilising interaction between the π orbital and the vinyl proton (see MO diagram).[1][2]
Appendix 1 shows possible conformers of 1,5-hexadiene. From this the antiperiplanar and gauche conformations found can be identified as anti1 and gauche3.
The anti2 conformer was drawn in GaussView. It was optimised at the H-F/3-21G level to give a total energy of -231.69253530 Hartrees (c.f. -231.69254 Hartrees in the appendix) and Ci point group. This output was then re-optimised at the higher B3LYP/6-31G* level to give an energy of -234.61170272 Hartrees. Out of the 10 energetically distinct conformers of 1,5-hexadiene, this is the global minimum.[1]
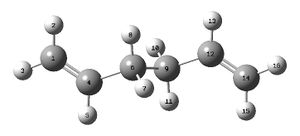
| Bond Length/Angle | H-F/3-21G | B3LYP/6-31G* |
|---|---|---|
| C=C | 1.32 Å | 1.33 Å |
| C-C (adjacent to C=C) |
1.51 Å | 1.50 Å |
| C-C (middle bond) |
1.55 Å | 1.55 Å |
| C(1)=C(4)-C(6) C(9)-C(12)=C(14) |
124.8° | 125.3° |
| C(4)-C(6)-C(9) C(6)-C(9)-C(12) |
111.3° | 112.7° |
The overall geometry changes very little when the molecule is re-optimised at the higher B3LYP/6-31G* level. The vinyl group C=C bond lengths and the two C-C bond lengths adjacent to the vinyl groups shorten when calculated at the higher level. The bond angles are slightly larger at the higher level. This is because B3LYP/6-31G* is a more accurate basis set than H-F/3-21G.
A frequency analysis was performed on the B3LYP/6-31G* optimised structure for two reasons. Firstly, to confirm that the structure is an energy minimum. The frequency analysis was performed at B3LYP/6-31G*. No negative/imaginary frequencies were found so the geometry was indeed an energy minimum.
Secondly, final energies found during the Gaussian optimisation represent the energy of the molecule on a bare potential energy surface. In order for these to be comparable with experimental quantities, additional terms must be included. These are found using a vibrational analysis.
| Sum of | Description | /Hartrees |
|---|---|---|
| electronic and zero-point energies | E = Eelec + ZPE at 0 K |
-234.469211 |
| electronic and thermal energies | E = Eelec + Evib + Erot + Etrans at 298.15 K and 1 atm |
-234.461854 |
| electronic and thermal enthalpies | H = E + RT | -234.460910 |
| electronic and thermal free energies | G = H - TS | -234.500826 |
Chair Transition Structure Optimisation
Force Constant Matrix Method
The CH2CHCH2 allyl fragment was drawn in GaussView and optimised using the HF/3-21G level of theory. The optimised fragment was used to produce a rough guess of the chair transition state, with the fragments positioned so that the terminal carbon atoms were approximately 2.2 Å apart.
If the approximate transition state structure is already known the easiest way to find the direction of negative curvature on the potential energy surface is to compute the force constant matrix, which is known as the Hessian. This is found in the first step of the optimisation and is updated as the optimisation proceeds.
An optimisation and frequency analysis was performed at the H-F/3-21G level on the guessed chair transition state. The structure was optimised to a transition state (Berny) and the force constants were calculated once.
The frequency calculation gave an imaginary vibrational frequency of magnitude 818 cm-1. Animation of the frequency in GaussView shows that it corresponds to the Cope rearrangement. An animation of the vibration can be viewed here.
Measurement of the distance between the terminal carbon atoms gives a bond breaking/forming distance of 2.02 Å. The energy of the transition structure was -231.61932244 Hartrees, c.f. -231.619322 Hartrees in the appendix.
Frozen Coordinate Method

If the guess for the transition state is very different to the actual transition state structure, then the force constant matrix method can fail because the direction of negative curvature may be significantly different at points far from the actual transition structure on the potential energy surface. In these cases it is best to use the frozen reaction coordinate method, in which the structure is optimised whilst the reaction coordinate is frozen. The coordinate is then unfrozen and the transition state optimisation performed. The whole Hessian does not have to be calculated and differentiating the reaction coordinate can be sufficient to find the transition state. This is much cheaper in terms of computational resources.
The guessed chair transition state was opened in GaussView and the redundant coordinate editor was used to freeze the coordinate at 2.2 Å between the allyl fragment terminal carbon atoms which form or break a bond during the rearrangement. The structure was then optimised at the H-F/3-21G level.
After this optimisation, the bond breaking/forming distances are optimised. The breaking/forming bonds were set to 'bond' and then the structure was optimised, with no force constant calculation, to a transition state at the H-F/3-21G level.
By measuring the distance between the terminal carbons in the output, the bond forming/breaking lengths were found to be 2.02 Å, the same length as for the force constant matrix method. The energy of the transition structure was -231.61932239 Hartrees, c.f. -231.619322 Hartrees in the appendix.
Boat Transition Structure Optimisation
QST2 method
In this method, the reactants and products are specified and the calculations interpolates between the two structures to try to find the transition state between them.
The output of the B3LYP/6-31G* anti2 optimisation was copied and pasted twice, into two separate groups, i.e. the reactant and product. The carbon label numbering was modified so that the product molecule had the same labelling as if the reactant had rearranged. An optimisation to TS (QST2) and frequency analysis was performed to the HF/3-21G level of theory.
The job fails because the QST2 method simply translated the top allyl fragment and did not consider the rotation of central bonds. The QST2 method cannot locate the boat transition structure from these reactant and product structures.
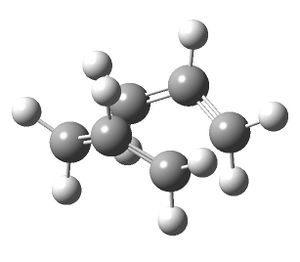
The input file was modified so that the middle C-C bond dihedral angle was 0° and the C-C-C angle either side of the central bond was 100°. The same optimisation and frequency analysis was successfully performed. An imaginary vibrational frequency of magnitude 840 cm-1 was found which corresponds to the bond forming/breaking in the Cope rearrangement. The energy of the transition structure was -231.52387276 Hartrees, c.f. -231.602802 Hartrees in the appendix.
Intrinsic Reaction Coordinate Method
It is almost impossible to predict which conformer of 1,5-hexadiene the reaction paths from the transition structures will lead to. The intrinsic reaction coordinate (IRC) method in Gaussian allows the minimum energy path from the transition state to be followed down to the local minimum on the potential energy surface. This is calculated by taking small geometry steps in the direction of the largest gradient on the potential energy surface.
The chair transition structure found using the frozen coordinate method was used to set up a IRC calculation. Since the reaction coordinate is symmetrical, the IRC was calculated in the forward direction only. The force constants were calculated once at the beginning of the calculation and 50 points were considered along the intrinsic reaction coordinate.
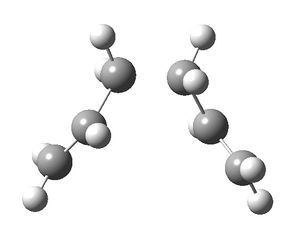
This calculation did not reach the minimum geometry. In order to reach the minimum geometry, the IRC was redone but the force constants were calculated at every step. The geometry obtained had an energy of -231.69166433 Hartrees. This corresponded to the gauche2 conformer, which has an energy of -231.69167 Hartrees in the appendix.
The Diels-Alder Cycloaddition
Introduction

The Diel-Alder cycloaddition is a pericyclic reaction, the simplest of which occurs between butadiene and ethylene. The π orbitals of the dienophile, ethylene, form new σ bonds with the π orbitals of the diene, butadiene, in a concerted fashion. The reaction is allowed when the HOMO of one reactant can overlap significantly with the LUMO of another reactant. If the HOMO and LUMO are of different symmetry then no overlap is possible and the reaction is forbidden.
Substituted dienophiles with substituents that have π orbitals that interact with the new double bond formed can stabilise the regiochemistry and favour one regioisomer over another.
Ethylene HOMO and Butadiene LUMO
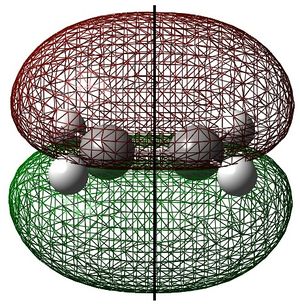
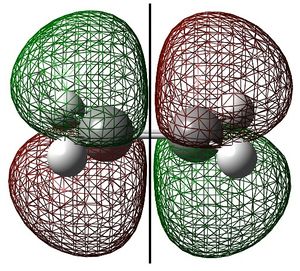
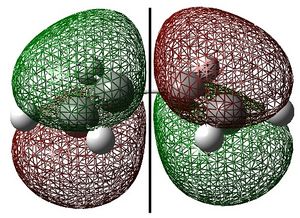
Ethylene and cis-butadiene were drawn in GaussView. They were optimised to the AM1 level of theory and their highest occupied and lowest unoccupied molecular orbitals are shown below. The symmetry of the molecular orbitals - either symmetric (s) or antisymmetric (a) with respect to the symmetry plane are shown.
 |
 |
 |
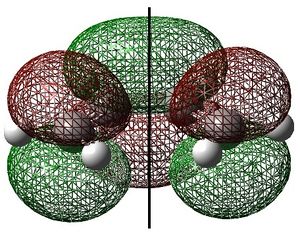 |
These show that the ethylene HOMO and butadiene LUMO are both symmetric with respect to the symmetry plane. Consequently, the ethylene HOMO and butadiene LUMO can overlap significantly enough for the reaction to be allowed. The reaction begins with the donation of electron density from the ethylene HOMO into the butadiene LUMO, breaking the C=C bonds. The reaction then proceeds via the concerted mechanism shown in the reaction scheme.
Calculation of Transition State Geometry
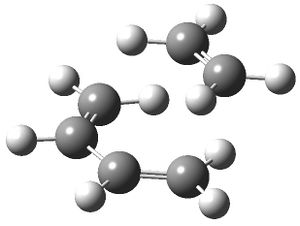
Ethylene, butadiene and cyclohexene were drawn in GaussView then optimised at the H-F/3-21G level of theory.
The optimised ethylene and butadiene fragments were then positioned so that the HOMO and LUMO orbitals would overlap significantly in order to make a guess at the transition state geometry. The fragments were positioned so that the terminal butadiene carbon atoms were 2.2 Å from the ethylene carbon atoms.
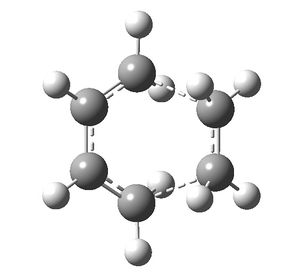
The cyclohexene product was then pasted in as a new molecule group. The atom labels were then modified so that they were consistent in the reactants and product. The structures were then optimised to a transition state using the QST2 method and a frequency analysis was performed. Both were calculated to a H-F/3-21G level of theory.
 |
 |
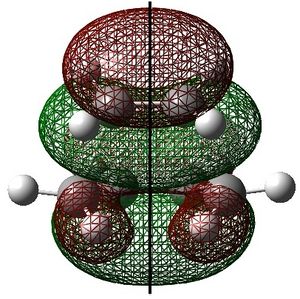 |
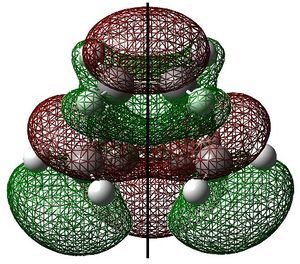 |
The ethylene HOMO (s) and butadiene LUMO (s) overlap to form the transition state. This is allowed because the HOMO and LUMO are of the same symmetry. The reaction starts with electron density from the ethylene HOMO being donated into the butadiene LUMO, which breaks the C=C bonds. The symmetry of the reactants is preserved through to the transition state.
An imaginary vibrational frequency of magnitude 819 cm-1 confirms that this is the transition state. An animation of the transition state vibration can be viewed here. The formation of the two σ bonds is synchronous; they form in a concerted fashion. The imaginary frequency is different to the lowest real vibrational frequency at 166 cm-1 in which the ethylene and butadiene rotate in opposite directions to one another.
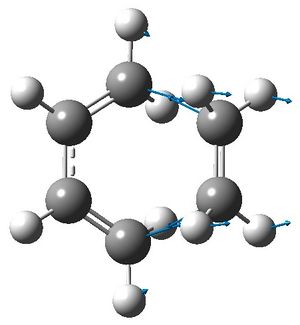 |
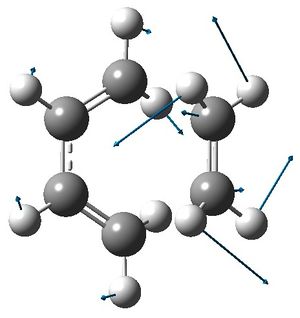 |
In the transition state, the terminal carbon atoms in butadiene are 2.21 Å from the ethylene carbon atoms. In comparison, typical sp3 and sp2 C-C bond lengths are 1.54 Å and 1.33 Å and the van der Waals radius of carbon is 1.70 Å.[3] From this, the length of the σ bonds forming in the transition state seem reasonable, as they are less than the length of twice the van der Waal radius and greater than the length of a typical C-C bond.
Reaction of Cyclohexa-1,3-diene with Maleic Anhydride
The same QST2 method used to determine the transition state geometry for the Diels-Alder reaction of ethylene and butadiene was also used to determine the geometry of the transition states in the Diels-Alder reaction between cyclohexa-1,3-diene and maleic anhydride. The endo product is predominantly formed over the exo product.
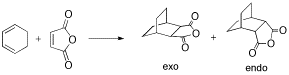
All reactants and products were drawn in GaussView and optimised at the H-F/3-21G level of theory. Guesses at the transition structures were made, with the maleic anhydride positioned approximately 2.2 Å from the cyclohexadiene. The product was added as a separate molecule group and the atom labels modified accordingly. The structures were then optimised to a TS using the QST2 method and a frequency analysis performed at the H-F/3-21G level of theory.
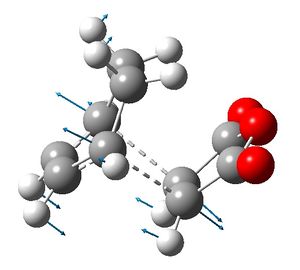
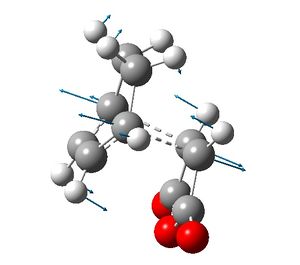
The exo and endo transition structures were successfully found with imaginary vibrational frequencies at 648 cm-1 and 648 cm-1 respectively. The energies of the transition states were -605.60359115 Hartrees and -602.61036823 Hartrees respectively, so the endo transition state is more stable than the exo transition state.
 |
 |
The bond lengths in the transition structures are tabulated below. The σ bond being formed is highlighted.
| Bond | Bond Length/Å | |
| Exo | Endo | |
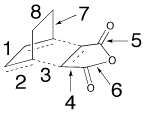
|
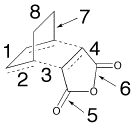
| |
| 1 | 1.40 | 1.40 |
| 2 | 1.37 | 1.37 |
| 3 | 2.26 | 2.23 |
| 4 | 1.48 | 1.48 |
| 5 | 1.19 | 1.19 |
| 6 | 1.40 | 1.39 |
| 7 | 1.52 | 1.52 |
| 8 | 1.56 | 1.56 |
Bonds 1 and 2 which are forming and losing a double bond respectively are of similar length. This supports the idea that the reaction forms via a transition state rather than an intermediate. The bonds are half-way between the reactants and products and are therefore very similar in terms of bonding.
The exo transition structure is a compromise between the steric repulsions of the -CH2-CH2- fragment from cyclohexadiene and the maleic ahydride. The distance between the -(C=O)-O-(C=O)- fragment and the opposite cyclohexadiene -CH2-CH2- fragment was 2.92 Å.
The endo transition structure is a compromise of secondary orbital interactions between the π systems of the cyclohexadiene -CH=CH- fragment and maleic anhydride -(C=O)-O-(C=O)- fragment. The distance between the -(C=O)-O-(C=O)- fragment and the opposite cyclohexadiene -CH=CH- fragment was 2.85 Å.
The σ bonds being formed are longer in the exo transition structure than in endo transition structure. This is because the steric repulsion in the exo transition structure does not allow the the fragments to get as close together as in the endo structure. The effect of the secondary orbital interactions in the endo transition structure is less than severe than the steric repulsion in the exo transition structure, in terms of the σ bonds being formed.
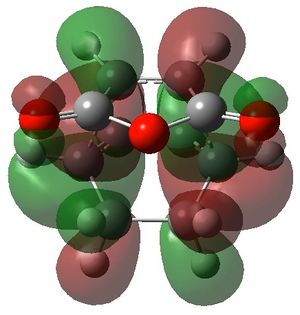 |
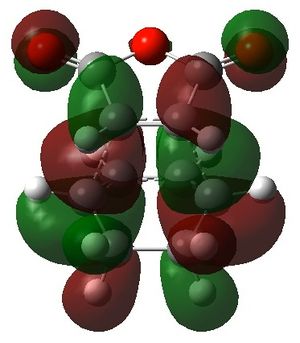 |
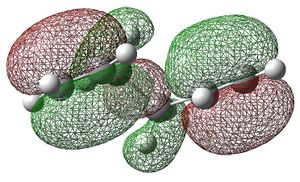
For the secondary orbital overlap in the endo transition state, there is a node between the maleic anhydride -(C=O)-O-(C=O)- fragment and the cyclohexadiene -CH=CH- fragment in the HOMO. The node, where there is no electron density, is shown in the plot of the HOMO. This interaction is not present in the exo transition state.
The secondary orbital overlap effect explains the preference for the endo isomer over the exo isomer. It is defined as the positive overlap of a non-active frame in the frontier molecular orbitals of a pericyclic reaction.[4] There is positive, stabilising orbital overlap between the HOMO located around the oxygen atoms in the maleic anhydride fragment and the LUMO located around the C=C bond being formed in the cyclohexadiene fragment. This secondary interaction stabilises the endo TS and is not present in the exo TS. Hence, the endo TS is more stable overall and the reaction gives predominantly the endo product.
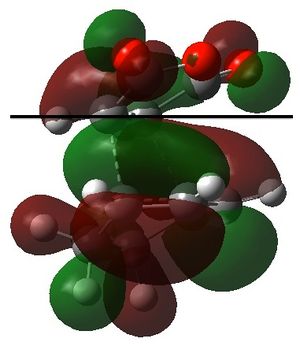 |
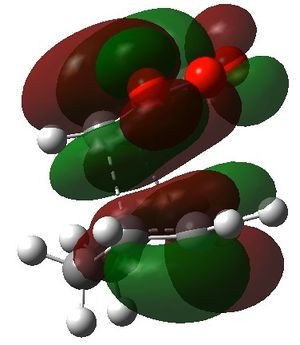 |
The solvent used in a Diels-Alder reaction can significantly change the rate and/or selectivity.[5][6][7] Therefore, in order to fully understand the reaction, solvents must be taken into consideration in the calculations.
References
- ↑ 1.0 1.1 B. W. Gung, Z. Zhu and R. A. Fouch, J. Am. Chem. Soc., 1995, 117 (6), 1783-88. DOI:10.1021/ja00111a016
- ↑ M. Nishio and M. Hirota, Tetrahedron, 1989, 45 (23), 7201-7245. DOI:10.1016/S0040-4020(01)89185-7
- ↑ D. R. Lide (ed.), W. M. Haynes (ed.), G. Baysinger (ed.), L. I. Berger (ed.), M. Frenkel (ed.) and R. N. Goldberg (ed.), CRC Handbook of Chemistry & Physics, 90th edn., 2009, Section 9, p. 49.
- ↑ M. A. Fox, R. Cardona and N. J. Kiwiet, J. Org. Chem., 1987, 52, 1469-74. DOI:10.1021/jo00384a016
- ↑ J. F. Blake and W. L. Jorgensen, J. Am. Chem. Soc., 1991, 113, 7430-2.
- ↑ C. Cativiela, J. I. García, J. Gil, R. M. Martínez, J. A. Mayoral, L. Salvatella, J. S. Urieta, A. M. Mainar and M. H. Abraham, J. Chem. Soc., Perkin Trans. 2, 1997, 653-60.
- ↑ R. Breslow, U. Maitra and D. Rideout, Tet. Lett., 1983, 24 (18), 1901-4. DOI:10.1016/S0040-4039(00)81801-8

