Rep:Mod:twporganic
Cyclopentadiene
Cyclodimerisation of cyclopentadiene
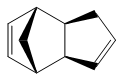
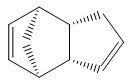
Cyclopentadiene dimerises to produce the endo dimer 2 rather than the exo isomer 1. By optimizing the geometries of both isomers using the MM2 force field in ChemBio3D, it was found that the energy of endo cyclodimerisation isomer 2 was 142 kJ/mol (3 s.f.) whereas the exo product 1 was 133 kJ/mol (3 s.f.), 9 kJ/mol lower in energy. Consequently, the cyclodimerisation of cyclopentadiene yields the kinetic product 2 rather than the more stable, thermodynamic product 1.
Components of Overall Energy
The MM2 force field output details quantitatively each of the factors contributing to the overall energy of the molecule.
| Component | Exo Dimer 1 | Endo Dimer 2 |
|---|---|---|
| Stretch | 2.00 | 2.04 |
| Bend | 33.2 | 32.8 |
| Stretch-Bend | -1.33 | -1.33 |
| Torsion | 15.2 | 12.2 |
| Non-1,4 VdW | -2.39 | -2.26 |
| 1,4 VdW | 6.87 | 6.75 |
| Dipole/Dipole | 0.710 | 0.602 |
| Total Energy | 54.2 | 50.8 |
The largest and second largest components of the overall energy for both molecules are bending and torsional strain respectively. This is expected as 5-membered rings are slighty strained. Overall, exo dimer 1 is thermodynamically less stable than endo dimer 2 because the magnitude of the torsional component is larger in the former than the latter. In both compounds, the stretch-bend and non-1,4 Van der Waals components are negative and therefore stabilising.
Hydrogenation of Cyclopentadiene Dimer
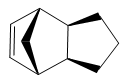
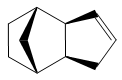
The endo dimer 2 can be hydrogenated to produce either 3 or 4. Using the same MM2 force field method, it was found that dihydro derivative 3 has an energy of 154 kJ/mol (3 s.f.) whereas dihydro derivative 4 has an energy of 122 kJ/mol (3 s.f.), 32 kJ/mol lower. Hence, 4 is thermodynamically more stable than 3 and stoichiometric hydrogenation of dicyclopentadiene would produce 4. This is in agreement with experiments reported in literature.[1]
Components of Overall Energy
The MM2 force field output details quantitatively each of the components contributing to the overall energy of the molecule.
| Component | Dihydro Derivative 3 | Dihydro Derivative 4 |
|---|---|---|
| Stretch | 1.96 | 1.81 |
| Bend | 29.8 | 20.8 |
| Stretch-Bend | -1.19 | -0.899 |
| Torsion | 20.4 | 19.8 |
| Non-1,4 VdW | -2.13 | -2.14 |
| 1,4 VdW | 9.62 | 7.06 |
| Dipole/Dipole | 0.260 | 0.225 |
| Total Energy | 58.8 | 46.6 |
As in the case of endo dimer 1 and exo dimer 2, the largest and second largest contributions to the overall energy of both dihydro derivative 3 and 4 are due to bending and torsional strain respectively; this would be expected as 5-membered rings are slighty strained. Again, in both compounds, the stretch-bend and non-1,4 Van der Waals components are negative and therefore stabilising.
The significant difference between the two derivatives is that In dihydro derivative 3, the bending component is 9.0×10-3 Hartree greater than that in dihydro derivative 4.
Stereochemistry of Nucleophilic Additions to a Pyridinium Ring (NAD+ Analogue)
Alkylation of Prolinol Derivative[2]
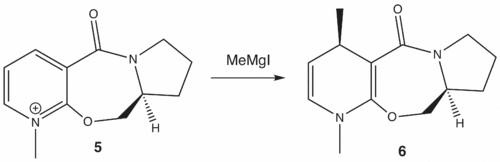
ChemBio3D was used to construct a model of prolinol derivative 5. Methyl magnesium iodide was not included in the model as ChemBio3D cannot assign an atom type (which takes into account the atom's contribution to bond energies and other characteristics, not just bond angles and lengths) to the magnesium atom in the MM2 force field calculation.[3]
The position of the carbonyl group relative to the pyridinium ring determines the stereochemistry of the added methyl group, since the methyl magnesium iodide first complexes to the carbonyl oxygen before the methyl adds to the ring. The methyl group can only add to the same face as the carbonyl oxygen.
Prolinol derivative 5 was drawn in ChemBio3D. The carbonyl dihedral angle relative to the pyridinium ring was systematically varied and then MM2 minimisation was performed in order to find different conformers and their overall energy.
| Initial Angle/° | Post-MM2 Angle/° | Energy/103 Hartree |
|---|---|---|
| 44 | 23 | 59.4 |
| 80 | 24 | 59.4 |
| 0 | 23 | 59.4 |
| -20 | 24 | 59.4 |
| -40 | 23 | 59.4 |
| -60 | 23 | 59.4 |
| -80 | 23 | 59.4 |
| -100 | 23 | 59.4 |
| -120 | -102 | 266 |
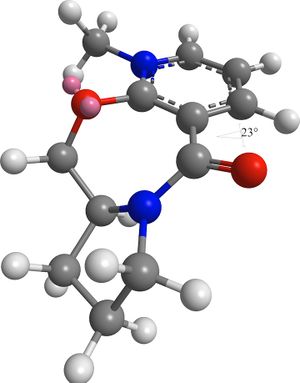
The results show that the lowest energy and hence most thermodynamically stable conformation of 5 is when the dihedral angle is 23°. The carbonyl group is pointing above the ring.
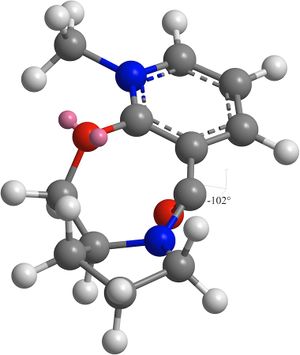
A second conformation with a dihedral angle of -102° has the carbonyl group pointing below the ring. This conformation is over four times higher in energy than the previous conformation.
Since the lowest energy conformation is with the carbonyl above the ring and the methyl group cannot reach around to the other side, it is delivered to the same face. Hence the geometry shown in reaction 1 is observed.
 |
 |
Addition of NHPh[4]
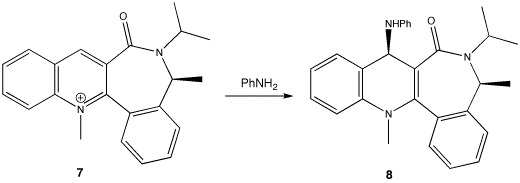
Unlike reaction 1, the nucleophile does not first complex to the carbonyl oxygen; PhNH2 does not have any electropositive elements to do so. PhNH2 will avoid the carbonyl group because of electrostatic repulsion between the lone pairs on the nitrogen and oxygen. Consequently, the PhNH2 nucleophile will add to whichever side is opposite to that of the carbonyl.
The same method used in reaction 1 was used to determine the lowest energy conformation of 7.
| Initial Angle/° | Post-MM2 Angle/° | Energy/103 Hartree |
|---|---|---|
| 30 | -20 | 101 |
| 50 | -20 | 101 |
| 70 | -20 | 101 |
| 90 | -20 | 101 |
| 110 | 120 | 289 |
The results show that the highest energy conformation of 7 is when the carbonyl dihedral angle is 120° above the ring. The lowest energy and hence most thermodynamically stable conformation of 7 is when the carbonyl dihedral angle is 20° below the ring.
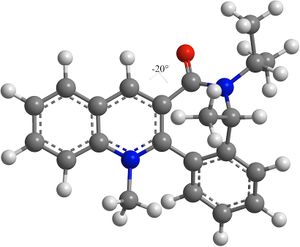 |
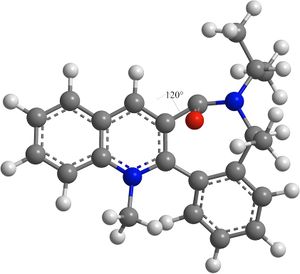 |
Consequently, PhNH2 attacks from above the ring to give 8 with the stereochemistry shown in reaction 2.
Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol
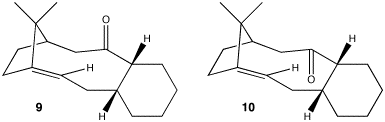
Stereochemistry
In the synthesis of taxol an intermediate is synthesised with the carbonyl group pointing either up or down. The stereochemistry of the carbonyl addition depends on which isomer is the most stable.
Both isomers were drawn in ChemBio3D and energies minimised using the MM2 force field. It was found that isomer 10 with the carbonyl group pointing down was most stable, with an energy of 228 kJ/mol (3 s.f.), in comparison to isomer 9 with an energy of 525 kJ/mol (3 s.f.).
However, closer inspection revealed that the cyclohexane ring plays an important role in the overall energy of the molecules. Cyclohexane can adopt a chair, boat or twist-boat conformation. The boat and twist-boat conformations are approximately 25 kJ mol-1 and 4 kJ mol-1 higher in energy than the chair conformation respectively.[5]
In the case of isomer 10 where the carbonyl group is pointing down, the cyclohexane ring had adopted a twist-boat conformation. The atoms in the ring were moved so that it was in a chair conformation and then the MM2 minimisation was performed. This gave an energy of 204 kJ/mol (3 s.f.), 24 kJ/mol lower in energy than the corresponding twist-boat conformation.
In the case of isomer 9 where the carbonyl group is pointing up, the cyclohexane ring had adopted the lowest energy chair conformation. Therefore twist-boat and boat conformations were not produced.
In conclusion, the lowest energy and therefore most stable isomer is 10.
 |
 |
Alkene Reactivity
It is noted that subsequent functionalisation of the alkene is abnormally slow. This is due to the alkene's hyperstability. In ChemBio3D, the alkene in the chair conformation of isomer 10 was changed to a single bond and then the MM2 minimisation was performed to give an overall energy of 235 kJ/mol (3 s.f.), c.f. 204 kJ/mol (3 s.f.) for the alkene. This shows that the alkene is exceptionally stable and that the molecule increases in energy when the bond is hydrogenated. The table below shows the components that contribute to the overall energy of 10 and its hydrogenated derivative; the increase in energy when the alkene is hydrogenated is mostly due to increased torsion.
| Component | Alkane | Alkene |
|---|---|---|
| Stretch | 4.80 | 4.19 |
| Bend | 26.0 | 24.2 |
| Stretch-Bend | 0.933 | 0.466 |
| Torsion | 33.8 | 29.3 |
| Non-1,4 VdW | -0.151 | -1.03 |
| 1,4 VdW | 24.0 | 20.5 |
| Dipole/Dipole | 0.00 | 0.0548 |
| Total Energy | 89.4 | 77.7 |
Regioselective Addition of Dichlorocarbene
Regioselectivity

Compound 12 was drawn in ChemBio3D. The energy was minimised using the MM2 force field in order to 'tidy up' the geometry. Both MOPAC/PM6 and MOPAC/RM1 molecular orbital methods were used to determine that the HOMO is located around the endo alkene bond nearest to the chlorine atom. Consequently, the endo alkene bond is the most nucleophilic and will be selectively attacked by dichlorocarbene. This is in agreement with literature.[6] In addition to the HOMO, the HOMO-1, LUMO, LUMO+1 and LUMO+2 of 12 were viewed using the same method and these are all shown below.
- Selected Molecular Orbitals of 12
-
HOMO-1
-
HOMO
-
LUMO
-
LUMO+1
-
LUMO+2
Vibrational Frequencies
The post-MOPAC/PM6 molecular structures of 12 and the dihydro equivalent 13 were then used to create a B3LYP/6-31G(d,p) Gaussian geometry optimization and frequency calculation input files. These were submitted to SCAN and the output files opened with GaussView in order to obtain the IR stretching frequencies. Results are shown below. Assigned frequencies were confirmed using the 'animate vibration' feature in GaussView.
| Compound | Bond | Frequency/cm-1 |
|---|---|---|
| 12 | C=C (endo) | 1737 |
| C=C (exo) | 1757 | |
| C-Cl | 771 | |
| 13 | C=C | 1758 |
| C-Cl | 775 |
C-Cl Bond
The C-Cl vibrational frequency in dihydro equivalent 13 is 4 cm-1 higher than the same bond in 12; hence, the monoene 13 C-Cl bond is stronger than the diene 12 C-Cl bond. This is because in the diene the occupied πC=C orbital overlaps with the empty σ*C-Cl orbital. The former donates electron density into the latter, weakening the bond. This does not occur in the monoene 13 as there is no πC=C orbital to overlap with the σ*C-Cl orbital.
C=C Bond
In 12 the exo C=C bond (1757 cm-1) is stronger than the endo C=C bond (1737 cm-1). The endo bond is weakened because of the destabilising orbital overlap between nCl and empty π*C=C. There is almost no difference in vibrational frequency for the exo C=C bond for 12 and 13, which one would expect as there is no difference between the molecular orbitals.
Mini-project: Asymmetric Total Synthesis of (+)-Crassalactone D
Introduction
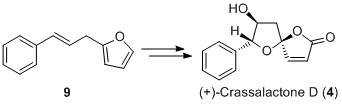
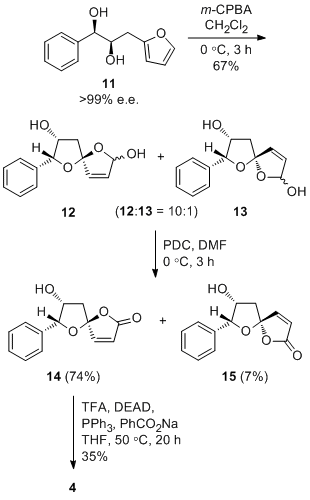
The asymmetric total sythesis of (+)-crassalactone D, a naturally occuring antitumor agent, by Yang et al[7] was achieved with the stereoselective spirocyclization of furan 11 as the key step to give lactols 12 and 13 in the ratio 10:1 respectively. These then underwent selective oxidization to 7-epi-crassalactone D (14) and 5-epi-7-epi-crassalactone D (15), which were separated by chromatography in 74% and 7% yield respectively. 7-OH in 14 was inverted to give desired product 4. Please note that numbering of compounds in this section of the report match those in the original literature in order to avoid confusion.
The key stereochemical step in the synthesis is the expodiation of 11 to give diastereomers 12 (74%) and 13 (7%) with S and R configurations at the spiroketal chiral center respectively. Yang et al provide do not provide spectroscopic data for 13, butthey do for the selective oxidation products 14 and 15. Since the chirality is unchanged, 14 and 15 will be considered in this analysis. Both compounds are fairly rigid and do not have many conformations in contrast to, for example, a compound with 6-membered rings and ester functional groups, and should not cause any problems performing calculations.
Key Spectroscopic Differences of 14 and 15
NMR
NMR Coupling Constants & Determination of Stereochemistry
In 1H NMR, one would typically look at coupling constants to provide stereochemical information. Unfortunately there are no 3J H couplings across the chiral centre which would provide some conformational information (through the use of the Karplus equation), since there are no H atoms within 3 bonds of one another across the chiral centre. There is a diastereotopic CH2 group adjacent to the chiral centre which will give two proton signals in a 1H NMR spectrum. These will couple with one another to give a doublet of doublets (typical 2J coupling of 14 Hz). However, this is not useful in differentiating between 14 and 15 because, again, there is not a third proton on the chiral centre to create an ABX system.
The 13C NMR spectra for diastereomers 14 and 15 will be very similar. Whilst this is not very useful in determining the stereochemistry, it would be useful in determining that the two samples extracted from the chromatography column are enantiomers.
Nuclear Overhauser Effect
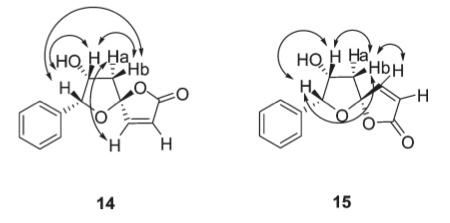
In a normal 1H NMR experiment, a broad pulse of radiowaves applied to the sample excites the spins of all the protons and the signal observed is generated by the protons dropping back down to their ground state. The process of the protons returning to their ground state is not spontaneous and relies on relaxation: nearby protons cause a proton's spin to drop back down.
In 1H NMR proton relaxation is fast and the number of nearby protons does not affect the obtained spectrum. However, it is possible to selectively irradiate specific protons in a compound. The causes the enhancement of nearby protons in the spectrum by a few percent and is called the nuclear Overhauser effect (NOE). The key difference between this and spin coupling is that the former occurs through space whereas the latter occurs through bonds. This effect can be and was used by Yang et al to distinguish between 14 and 15; their correlation diagram is shown to the right. Unfortunately, the NOE cannot be predicted using Gaussian or ChemBio3D.
Optical Rotation
Enantiomers of compounds with one chiral centre have identical physical and chemical properties except for their ability to rotate a plane of polarized light in equal and opposite directions. Thus enantiomers of a compound can be distinguished by measuring their optical rotation. Since 14 and 15 are diastereomers, not enantiomers, their optical rotations will not be equal and opposite, but will be different. The optical rotation of 14 and 15 can be predicted and then one could compare the measured optical rotation of a sample to determine which diastereomer it is.
13C NMR
Prediction using GIAO Method
Compounds 14 and 15 were drawn in ChemBio3D. The geometry of both compounds were successfully optimised by minimising the energy using MM2 then MOPAC/AM1 for 'fine tuning'. Gaussian input files were generated for the GIAO NMR calculation, with the following parameters:
RMPW1PW91/6-31G(d,p) NMR=GIAO SCRF=(CPCM,Solvent=Chloroform)
Results are tabulated below. See diagrams for carbon atom labels. Please note the atom labels on spectra correspond to the automatic labelling in GaussView; these were then changed so only carbon atoms were numbered and it is these that are shown in the following tables.
 |
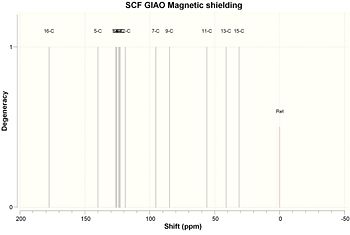 |
| Carbon | Chemical Shift/ppm |
|---|---|
| 1 | 177.696 |
| 2 | 139.779 |
| 3 | 126.357 |
| 4 | 125.718 |
| 5 | 124.171 |
| 6 | 123.22 |
| 7 | 122.928 |
| 8 | 118.76 |
| 9 | 95.2402 |
| 10 | 84.8046 |
| 11 | 56.0229 |
| 12 | 41.324 |
| 13 | 31.0719 |
 |
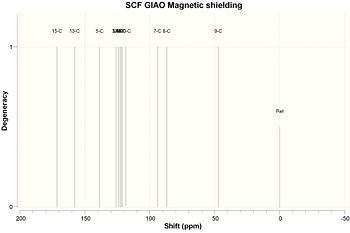 |
| Carbon | Chemical Shift/ppm |
|---|---|
| 1 | 171.394 |
| 2 | 157.936 |
| 3 | 138.437 |
| 4 | 126.054 |
| 5 | 125.951 |
| 6 | 124.389 |
| 7 | 122.879 |
| 8 | 122.333 |
| 9 | 121.204 |
| 10 | 118.624 |
| 11 | 93.8831 |
| 12 | 86.9157 |
| 13 | 47.0377 |
Comparison of Literature and Predicted Spectra
The chemical shifts of the carbon in the ester carbonyl environment have been corrected using δcorr = 0.96δcalc + 12.2 (taken from Mod:organic).
Since the aromatic ring will undergo rapid rotation in solution and the calculations consider the molecule to be a static system, the predicted peaks for carbon atoms 3 & 4 and 6 & 7 in 14 and carbon atoms 4 & 5 and 8 & 9 in 15 were averaged.
The predicted chemical shifts were then compared with the literature spectra[8] and the differences calculated. These have been tabulated and plotted below.
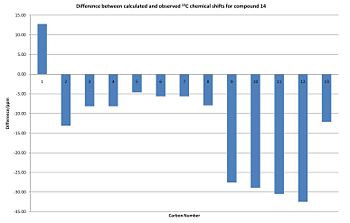
| Carbon | Predicted Chemical Shift/ppm | Observed Chemical Shift/ppm | Δ/ppm | Δ2/ppm2 |
|---|---|---|---|---|
| 1 | 182.79 | 170.00 | 12.79 | 163.54 |
| 2 | 139.78 | 152.90 | -13.12 | 172.16 |
| 3 | 126.04 | 134.20 | -8.16 | 66.63 |
| 4 | 126.04 | 134.20 | -8.16 | 66.63 |
| 5 | 124.17 | 128.80 | -4.63 | 21.43 |
| 6 | 123.07 | 128.70 | -5.63 | 31.65 |
| 7 | 123.07 | 128.70 | -5.63 | 31.65 |
| 8 | 118.76 | 126.70 | -7.94 | 63.04 |
| 9 | 95.24 | 122.80 | -27.56 | 759.54 |
| 10 | 84.80 | 113.70 | -28.90 | 834.94 |
| 11 | 56.02 | 86.50 | -30.48 | 928.85 |
| 12 | 41.32 | 73.80 | -32.48 | 1054.69 |
| 13 | 31.07 | 43.20 | -12.13 | 147.09 |
| Σ(Δ2) = | 4341.85 |

| Carbon | Predicted Chemical Shift/ppm | Observed Chemical Shift/ppm | Δ/ppm | Δ2/ppm2 |
|---|---|---|---|---|
| 1 | 176.74 | 169.20 | 7.54 | 56.83 |
| 2 | 157.94 | 151.70 | 6.24 | 38.89 |
| 3 | 138.44 | 135.20 | 3.24 | 10.48 |
| 4 | 126.00 | 128.60 | -2.60 | 6.75 |
| 5 | 126.00 | 128.60 | -2.60 | 6.75 |
| 6 | 124.39 | 128.40 | -4.01 | 16.09 |
| 7 | 122.33 | 124.50 | -2.17 | 4.70 |
| 8 | 122.04 | 126.70 | -4.66 | 21.70 |
| 9 | 122.04 | 126.70 | -4.66 | 21.70 |
| 10 | 118.62 | 114.10 | 4.52 | 20.47 |
| 11 | 93.88 | 88.90 | 4.98 | 24.83 |
| 12 | 86.92 | 72.90 | 14.02 | 196.44 |
| 13 | 47.04 | 44.30 | 2.74 | 7.50 |
| Σ(Δ2) = | 433.10 |
Comments
Compound 14
The predicted spectrum for compound 14 is significantly different to the observed spectrum to the extent that the chemical shifts barely correlate; the sum of the squared differences for compound 14 is over ten times larger than that for compound 15. I do not know why this is the case as I had expected the spectra of the two compounds to be very similar.
Compound 15
The predicted spectrum for compound 15 matches the observed spectrum reasonably well. Interestingly, for carbon atoms 4 to 9 the predicted chemical shifts were all a few ppm lower than the observed chemical shifts. The predicted chemical shift for carbon 3 was 3.24 ppm higher than the observed chemical shift. This may be due to the calculation not taking into account rapid rotation of the aromatic ring.
Carbon atom 10 is bonded to two oxygen atoms. Hence, its bonding is not that dissimilar to the bonding in carbonyl carbon 1. The predicted chemical shift for carbonyl carbon 1 is corrected using δcorr = 0.96δcalc + 12.2, so it seems reasonable to also correct the predicted chemical shift for carbon atom 10. Doing so, however, significantly increases the difference between the predicted and observed chemical shift from 4.52 ppm to to 11.98 ppm. The same correction for carbonyl carbon 1 cannot be applied to carbon atom 10 and different correction needs to be determined.
The two largest errors are for carbon atoms 1 and 12. Both of these atoms are singly bonded to oxygen atoms. This suggests that this method is not very good at predicting the chemical shifts of carbon atoms adjacent to oxygen atoms.
Second Attempt at 13C NMR spectrum for Compound 14
Because of the significant differences between the predicted and observed 13C NMR spectrum for compound 14, a second attempt was made at predicting the spectrum. The compound was redrawn in ChemBio3D and the geometry was optimised using the MOPAC/AM1 method. A Gaussian input file was created with the same parameters as before and then submitted to SCAN. The results are shown below.
 |
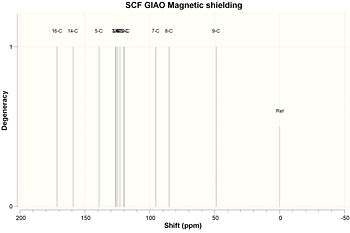 |
| Carbon | Chemical Shift/ppm |
|---|---|
| 1 | 171.52 |
| 12 | 159.33 |
| 2 | 139.03 |
| 8 | 119.65 |
| 13 | 120.65 |
| 6 | 122.94 |
| 7 | 123.02 |
| 5 | 124.46 |
| 4 | 125.85 |
| 3 | 126.43 |
| 10 | 85.35 |
| 9 | 95.27 |
| 11 | 48.92 |
As before, the carbonyl carbon predicted chemical shift was corrected and the chemical shift for carbons 3 & 4 and 6 & 7 were averaged to take into account rapid rotation of the aromatic ring. The predicted chemical shifts were then compared with the literature spectrum and the differences calculated. These have been tabulated and plotted below. The same carbon atom labels have been used.
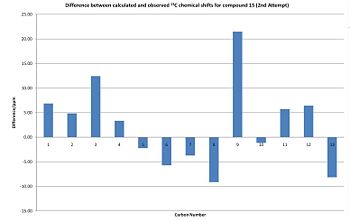
| Carbon | Corrected Chemical Shift/ppm | Observed Chemical Shift/ppm | Δ/ppm | Δ2/ppm2 |
|---|---|---|---|---|
| 1 | 176.86 | 170.00 | 6.86 | 47.01 |
| 12 | 159.33 | 152.90 | 6.43 | 41.37 |
| 2 | 139.03 | 134.20 | 4.83 | 23.33 |
| 8 | 119.65 | 128.80 | -9.15 | 83.72 |
| 13 | 120.65 | 128.80 | -8.15 | 66.39 |
| 6 | 122.98 | 128.70 | -5.72 | 32.71 |
| 7 | 122.98 | 126.70 | -3.72 | 13.83 |
| 5 | 124.46 | 126.70 | -2.24 | 5.01 |
| 4 | 126.14 | 122.80 | 3.34 | 11.14 |
| 3 | 126.14 | 113.70 | 12.44 | 154.70 |
| 10 | 85.35 | 86.50 | -1.15 | 1.32 |
| 9 | 95.27 | 73.80 | 21.47 | 461.04 |
| 11 | 48.92 | 43.20 | 5.72 | 32.69 |
| Σ(Δ2) = | 974.27 |
Comments
This spectrum prediction is significantly better than the first as Σ(Δ2) is much smaller than for the first prediction and I think that the huge difference between the first calculated and observed spectra was caused by user error. However, Σ(Δ2) for 14 is still approximately twice the size of Σ(Δ2) for 15. This suggests that this method of predicting the 13C NMR spectrum is less accurate for 14 than 15. The largest difference between the predicted and observed chemical shift is for carbon atom 9 and a correction needs to be applied to predicted chemical shifts for this environment.
NMR Summary
In order to decide whether a particular sample was either diasteromer 14 or15, one would first record 13C NMR spectrum. This would then be compared with the predicted spectra for both compounds. By matching the predicted and observed spectrum, the best match being the one with the smallest Σ(Δ2), one could decide what the sample is. However, I do not think it would be possible in this case because Σ(Δ2) is large for both diasteromers. For example, if the observed spectrum for 14 is compared with the predicted spectrum for 15, Σ(Δ2) = 511 (3 s.f.). This is in fact a better fit than when the observed spectrum of 14 is compared with the predicted spectrum of 14! As a result, 13C NMR could not be used to distinguish between 14 and 15.
Optical Rotation
Since the rotation of an OH group by only 60° can alter the value of [α] by as much as a factor of two, it is important that the correct geometry is determined. The structures used to predict the NMR spectra were subjected to further geometry optimisation using MOPAC/AM1. The optimised structures were then used to calculate the optical rotation using following job type:
# b3lyp/aug-cc-pvdz polar(optrot) scrf(IEFPCM,solvent=chloroform) CPHF=RdFreq Optical rotation for compound x 0 1 firstatom-symbol 0 x-cooordinate of atom1 2-cooordinate of atom1 -cooordinate of atom1 ... lastatom-symbol 0 x-cooordinate of lastatom 2-cooordinate of lastatom -cooordinate of lastatom 589nm
Results are shown in the table below.
| Compound | Measured [α]20D | Calculated [α]20D |
|---|---|---|
| 14 | -64.5° | +33.7° |
| 15 | -48.2° | +54.1° |
The calculated values are significantly different to those measured by Yang et al to the extent that absolute signs are incorrect for both compounds. It is generally accepted among computational chemists that calculations can only reliably calculate optical rotations for compounds with [α] > +/- 100°. The smaller the magnitude of the optical rotation the lower the reliability of the calculation. Optical rotation calculations are also highly senstive to conformation. As already said, rotation of an OH group by as little as 60° can alter [α] by as much as a factor of two.
If more time were available, it might have been worth trying to optimize the geometry again but using the Hartree-Fock method and a STO-3G basis set in Gaussian, and then performing the optical rotation calculation on this structure. However, I have doubts whether this would have worked because the measured values are << 100%deg;. This method would be better at distinguishing betweeen enantiomers rather than diastereomers, because the former have optical rotations that are of equal amounts but opposite directions, whereas the latter can have different amounts and not neccessarily opposite directions, as in the case of 14 and 15.
References
- ↑ G. Liu, Z. Mi, L. Wang and X. Zhang, Ind. Eng. Chem. Res., 2005, 44 (11), 3846-51. DOI:10.1021/ie0487437
- ↑ A. G. Shultz, L. Flood and J. P. Springer, J. Org. Chem., 1986, 51, 838. DOI:10.1021/jo00356a016
- ↑ ChemBio3D Ulta 12.0 Help Article: "About Atom Types"
- ↑ S. Leleu, C. Papamicael, F. Marsais, G. Dupas and V. Levacher, Tet. Asym., 2004, 15, 3919-28. DOI:10.1016/j.tetasy.2004.11.004
- ↑ J. Clayden, N. Greeves, S. Warren and P. Wothers, Organic Chemistry, Oxford, 2007, pp. 457-9.
- ↑ B. Halton, R. Boese and H. S. Rzepa, J. Chem. Soc., Perkin Trans. 2, 1992, 447-8. DOI:10.1039/P29920000447
- ↑ Z. Yang, P. Tang, J. F. Gauuan and B. F. Molino, J. Org. Chem., 2009, DOI:10.1021/jo902055b
- ↑ Supporting Information