Rep:Mod:tts16
Part 1 and Part 2
NH3 Molecule
| Item | Values |
|---|---|
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy E(RB3LYP) | -56.55776873 a.u. |
| RMS Gradient | 0.00000485 a.u. |
| Point Group | C3v |
| Optimised N-H Bond Distance | 1.018 Angstroms |
| Optimised H-N-H Bond Angle | 105.741 Degrees |
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
NH3 |
The optimisation file for NH3 is linked to here
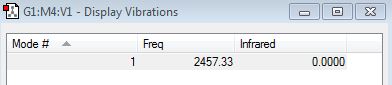
how many modes do you expect from the 3N-6 rule? 6 modes expected
which modes are degenerate (ie have the same energy)? Modes 2/3, Modes 5/6
which modes are "bending" vibrations and which are "bond stretch" vibrations? 1,2,3 are bending. 4,5,6 are stretching.
which mode is highly symmetric? Mode 4 is highly symmetric.
one mode is known as the "umbrella" mode, which one is this? Mode 1 is the umbrella mode.
how many bands would you expect to see in an experimental spectrum of gaseous ammonia? 4 bands are expected
The Nitrogen atom is negatively charged (-1.125), while the Hydrogens are positively charged (0.375). This is due the fact that Nitrogen is a very electronegative atom, thus has greater propensity to pull electrons closer to it relative to the hydrogen atoms. Therefore N is negatively charged and the H's are positively charged.
N2 Molecule
| Item | Values |
|---|---|
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy E(RB3LYP) | -109.52412868 a.u. |
| RMS Gradient | 0.0.00000060 a.u. |
| Point Group | D*H |
| Optimised N-H Bond Distance | 1.106 Angstroms |
| Optimised H-N-H Bond Angle | 180 Degrees |
N2 molecule |
The optimisation file for N2 is linked to here
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
There is only one mode for the N2 molecule.
H2 Molecule
| Item | Values |
|---|---|
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy E(RB3LYP) | -1.17853936 a.u. |
| RMS Gradient | 0.0.00000017 a.u. |
| Point Group | D*H |
| Optimised N-H Bond Distance | 0.74279 Angstroms |
| Optimised H-N-H Bond Angle | 180 Degrees |
H2 molecule |
The optimisation file for H2 is linked to here
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
There is only one mode for the H2 molecule.
Part 3
Haber-Bosch Process
E(NH3)= -56.55776873 a.u.
2*E(NH3)= -113.1155375 a.u.
E(N2)= -109.5241287 a.u.
E(H2)= -1.17853936 a.u.
3*E(H2)= -3.53561808 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.0557907 a.u. = -146.4784828 kj/mol
The ammonia product is more stable than its reactants (Hydrogen and Nitrogen gas) as shown by the energy values. The literature value is stated to be −45.7kJ/mol if one mole of ammonia is produced.[1] (Thus -91.4 kJ/mol for two moles of ammonia). This differs with the calculated value above, but the change in energies will also depend on reaction conditions.
Part 4
F2 Molecule
| Item | Values |
|---|---|
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy E(RB3LYP) | -199.49825218 a.u. |
| RMS Gradient | 0.0.00007365 a.u. |
| Point Group | D*H |
| Optimised N-H Bond Distance | 1.40281 Angstroms |
| Optimised H-N-H Bond Angle | 180 Degrees |
F2 molecule |
The optimisation file for F2 is linked to here
Item Value Threshold Converged?
Maximum Force 0.000128 0.000450 YES
RMS Force 0.000128 0.000300 YES
Maximum Displacement 0.000156 0.001800 YES
RMS Displacement 0.000221 0.001200 YES
Fluorine is the most electronegative atom in the periodic table. However, in its diatomic form, the molecule F2 do not have a resulting net dipole as it is bonded with its identical atom. Therefore, there is no charge distribution in the molecule.
Molecular Orbitals Visualisation
Fluorine atoms have an electronic configuration of 1s22s22p5. With 7 electrons in the valence shell of each fluorine atom, within a molecular orbital diagram, the 2s bonding and anti bonding sigma bond will be filled. Higher up the energy diagram, the 2pz, 2px, 2px will be filled. The remaining 2 electrons from each fluorine atom will fill the pi-star 2px and pi-star 2py. Consequently, the fluorine molecule (F2) will form one sigma bond between the two atoms. The above snapshot shows a bonding combination of two 1s core atomic orbitals. In the column next to the molecule, it is noted that the energy is -24.797 a.u., which is much deeper in energy than the the molecular orbitals formed by the atomic orbitals in fluorine's valence shell. However, from the visualization it is seen that the 1s atomic orbitals of fluorine barely overlap; instead, they are held tightly to their respective nuclei and barely contribute to chemical bonding and are effectively non bonding orbitals.
The above snapshot is a visualization of the molecular orbital formed by the combination of the valence 2s orbitals of fluorine. Relative to the molecular orbital formed by the 1s atomic orbitals, it is evident that the overlap of the 2s atomic orbitals are much more stronger as what is visualized is simply one extended surface. As the 2s orbitals are valence orbitals of fluorine atoms, they contribute greatly to chemical bonding. As shown, the energies are much higher as well, with the bonding and anti-bonding orbitals at -1.09 to -1.34 a.u.
This snapshot is a visualization of the anti-bonding of the 2s valence atomic orbitals. As indicated by the green and red colour, the two wavefunctions are out of phase and thus do not overlap to create a bond.
This snapshot is a visualization of the molecular orbital formed by the combination of two 2pz atomic orbitals. This is a direct head on overlap of two pz orbitals and forms a sigma bond. The energy of this molecular orbital is noted as -0.588 a.u., just slightly lower than the two other px and y orbitals, as sigma bonds are lower in energy than pi bonds.
The above two snapshots are the molecular orbitals formed by two 2x and two y. These two molecular orbitals have the same energy of -0.523 a.u.ː the two orbitals are degenerate but in directions orthogonal to each other.
The above snapshot is a visualization of the anti-bonding of the 2p x orbital.(or (or 2p y orbitalː degenerate orbitals, but in a different orientation). As shown, the two wavefunctions are out of phase and do not overlap. The two anti-bonding orbitals effectively cancel out the bonding 2px and 2y orbitals, leaving only the 2pz as a bonding molecular orbital. Therefore, F2 has a bond order of one and is formed by a single bond.
References
- ↑ J. M. Modak, Resonance, 2017, 10.