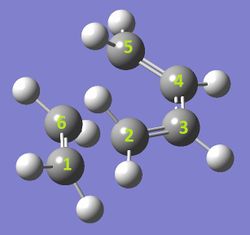
Rep:Mod:tsns2214

Transition States

Introduction

Potential energy surfaces display the energy of a system with respect to positions of the molecules. They can therefore be used to display transition states and minima. Transition states are an energy maximum where the first derivative of the energy surface is 0 at this point. The reactants and products will also have a gradient of 0 as they are local minima. In this lab, the transition states of Diels-Alder reactions were studied. This involves a [4+2] cycloaddition between a diene and dienophile. These double bonded structures are close enough in energy to interact and form 2 new sigma bonds and breaking one pi bond overall. The formation of theses sigma bonds lowers the energy of the system as electrons occupy bonding molecular orbitals. Additional effects such as aromaticity and secondary orbital overlap can also contribute to the product formation.

Nf710 (talk) 09:41, 7 April 2017 (BST) You need to talk about second derivatives here.

Gaussian software was used to analyse the transition state formation of three Diels-Alder reactions. Method 3 in the tutorial was used for all the reactions, where the expected product molecule was optimised, the relevant bonds broken and frozen, and then the resulting transition-like state optimised. Two levels of optimisation were used: PM6 semi-empirical for exercises 1 and 3 and B3LYP-DFT for exercise 2. PM6 uses relevant parameters to fit experimental dipole moments and geometries, allowing for faster results. B3LYP uses a mixture of Density Functional Theory and Hartree-Fock Theory. The two methods have contrasting functions: Hartree-Fock methods treat exchange correlation to a precise value and DFT has an exact value for dynamic electron correlation. If the correct transition state was found, there was one negative frequency found in the vibrations, corresponding to. Often PM6 optimisation is conducted before B3LYP to speed up optimisation to this level.

Nf710 (talk) 09:41, 7 April 2017 (BST) This is a fairly good understanding of the methods.

Several considerations have to be taken into account when studying Diels-Alder reactions. One is that the diene and dienophile's HOMO and LUMOs are are relatively close to each other. The smaller energy gap between a HOMO-LUMO pair depended on the nature of the reactants and their electron densities. The checkpoint files obtained from optimisations gave insight into the closer energy levels and thus explained the products formed. Another consideration was that a molecule, such as xylylene, could have multiple reaction sites or the molecules could approach each other at different geometries. Once transition state structures had been optimised, IRC analysis was conducted to confirm the transition state path. The IRC file also displayed the first derivative and if the structure had been correctly optimised, values of 0 were seen at the reactant, transition state and product. If there were multiple approach possibilities and transition state structures, the free energy data could be extracted from the log files, in order to find the thermodynamic and kinetic products.

Exercise 1: 1,3-Butadiene and Ethene

The first Diels-Alder reaction characterised was between 1,3-butadiene and ethene, forming cyclohexene. Visualising the molecular orbitals for the optimised reactants, products and transition state enabled for an orbital diagram to be drawn (Figure 1). It is evident that the formation of molecular orbitals is restricted by symmetry. Orbitals of the same symmetry/asymmetry can interact and bring stability to the molecule.

Figure 1 Cyclohexene MO Diagram

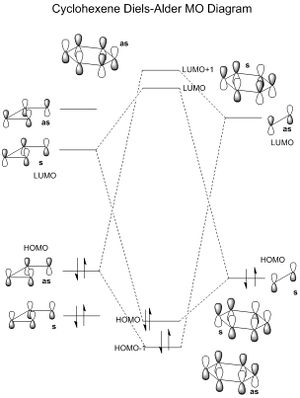
(Fv611 (talk) 15:34, 5 April 2017 (BST) Both the symmetric (HOMO/LUMO) TS MOs and the antisymmetric (HOMO-1/LUMO +1)ones are switched around: the interactions with lower energy are bonding ones, not antibonding ones. This would have been avoided if you had considered the angle at which the ethene approaches the butadiene.)

Looking at the values for the optimised reactants, the HOMO of the butadiene (-0.35899) and LUMO of the ethene (0.04256) are closer in energy and therefore the energy gap between the bonding and anti-bonding orbitals formed is larger. The energy difference between the HOMO ethene and LUMO butadiene is [(0.01943+0.39228)-(0.04256+0.35899)]=0.01006 larger giving a smaller energy gap in molecular orbitals formed. The orbital overlap is non-zero for a symmetric-symmetric or asymmetric-asymmetric interaction, and zero for an asymmetric-symmetric interaction, as in the latter interaction, one pair of p orbitals are in the phase and the other pair out of phase, effectively cancelling each other out.

.

Exercise 1 Molecular Orbitals

PM6	Ethene	Butadiene	Transition States
LUMO			LUMO+1
HOMO			HOMO-1

(Fv611 (talk) 15:34, 5 April 2017 (BST) Again, your TS MOs are completely in the wrong order: MO16 is the HOMO-1, MO17 is the HOMO, MO18 is the LUMO and MO19 is the LUMO+1. Paying attention to their relatives energies would have helped avoiding the mis-ordering.)

Carbon numbering and bond lengths (Å)
Figure 3 Carbon numbering used by Gaussian
	C1-C2/C5-C6	C2-C3/C4-C5	C3-C4	C6-C1
Reactants	-	1.333	1.471	1.327
Transition State	2.115	1.380	1.411	1.382
Product	1.537	1.501	1.337	1.535

Figure 2 Graph showing internuclear distances during cyclohexene formation

The graph in Figure 2 displays how the C-C bonds change in length as the reactants approach the transition state and then form the products. Well before the transition state is reached, all bond lengths remain constant except for C1-C2 and C5-C6 as the ethene and butadiene molecules approach each other. Typical sp² C-C bond length at this stage is around 1.336 Å. Just before the transition state is approached, C1-C2 and C5-C6 continue to descend, but the other bond lengths appear to converge as the cyclisation occurs.

The four bond lengths converge just after the transition state. The bond length between the newly forming C1-C2 and C5-C6 is 2.115 Å at the transition state. This is significantly smaller than the Van Der Waal's radius of two Carbon atoms (1.7x2= 3.4 Å). This suggests that bond formation is occurring throughout the transition state, especially as the bond length continues to decrease linearly and plateau at a value of ~1.54 Å, the typical C-C sp³ sigma bond length. What seems to define the transition state of cyclohexene is the convergence of the four other bond lengths

.

The vibration at the transition state has a negative frequency. Looking at the vectors displayed for this vibration, it appears that the bond formation is synchronous. Therefore only one stereoisomer forms from the Diels-Alder reaction as there is no possibility of bond rotation before the second bond forms.

Exercise 2: cyclohexadiene and 1,3,Dioxane

Exercise 2 Molecular Orbitals

B3LYP	EXO Transition States		ENDO Transition States
LUMO				LUMO+1
HOMO				HOMO-1

Figure 4 Cyclohexadiene and 1,3-Dioxole MO Diagram

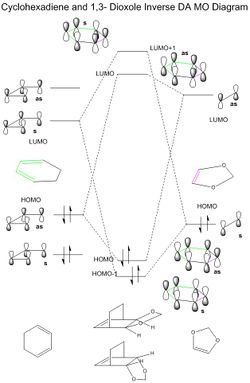
(Overlap between these pi orbitals occurs head-on in a sigma fashion. Review the MO diagram and compare to the MOs you have in the table above Tam10 (talk) 11:22, 3 April 2017 (BST))

Table of Activation and Reaction Energies (KJmol^-1)

(B3LYP level)	Reactants	Transition State	Product	Activation Energy	Reaction Energy
Exo	169.636	364.685	99.701	195.048	-69.935
Endo	169.636	362.167	99.254	192.531	-70.382

Following the progress of the reaction between cyclohexadiene and 1,3-dioxole produced different results to exercise 1. Here, a typical inverse demand Diels-Alder reaction was seen, where the diene's HOMO and dienophile's LUMO formed the molecular HOMO and LUMO orbitals of the transition state (Figure 4). Energy levels of the HOMO and LUMO for each reactant were obtained from the checkpoint files. The energy gap between the diene's HOMO and dienophiles's LUMO is 0.18589 and therefore smaller than the diene's LUMO and dienophiles's HOMO energy gap of 0.21191. The smaller energy gap results in greater splitting. The electron rich nature of the diene 1,3-dioxole is due to the oxygen atoms adjacent to the double bond. The mixing of these p orbitals raises the energy of the diene's HOMO and brings it closer to the dienophile's LUMO.

The Gibbs free energies were extracted from the log files of the reactants and transition states and the reaction barriers calculated accordingly (Figure 6). The endo-conformer of the product has a lower reaction barrier, being 7.842 KJmol^-1 smaller in value. This therefore makes it the kinetic product as less energy is required to overcome the barrier and thus over time, it will form more quickly. The stability of the transition state in the endo-form is most likely due to secondary orbital interaction. From the table and in Figure 5 it can clearly be seen in the transition state HOMO where the p orbitals of cyclohexadiene are able to interact with the oxygen p orbitals, bringing some stability to the transition state. The endo product also has a lower product energy, final value being 0.446 KJmol^-1 lower than the exo product, making it the thermodynamic product too.

Figure 5 Secondary Orbital Overlap in Endo Transition State

Figure 6 Reaction co-ordinate for Exercise 2

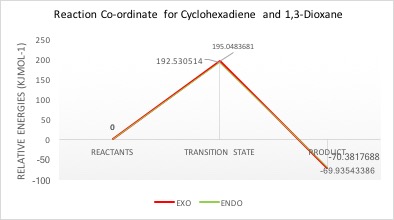
Nf710 (talk) 09:59, 7 April 2017 (BST) You have come up with some good conclusions in this section. However even though you have come out with the correct conculsions your results are still incorrect. Your reactions barriers are way off and one can only assume you have calculated your TS incorrectly.

Exercise 3: O-Xylylene-SO2 Cycloaddition

Table of Activation and Reaction Energies (KJmol^-1)

(PM6 level)	Reactants	Transition State	Product	Activation Energy	Reaction Energy
Exo	156.249	241.746	56.325	85.497	-99.924
Endo	156.249	237.765	56.965	81.517	-99.283
Chelotropic	156.249	260.087	3.277	103.839	-152.972
Unfavourable Exo	156.249	275.819	176.707	119.571	20.458
Unfavourable Endo	156.249	267.982	172.259	111.733	16.010

Figure 7 Reaction co-ordinate of 5 pathways

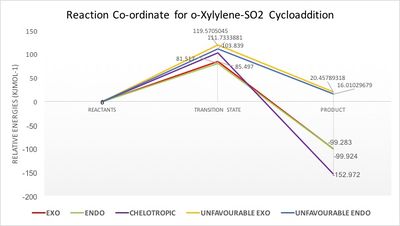
(Energy profile diagram to the right is a bit difficult to see. Some values are overlapping Tam10 (talk) 11:22, 3 April 2017 (BST))

Once again, the free energies of the reactants, transition states and products were extracted from the log files, optimised at the PM6 level. The relative energies of the pathways created are shown in Figure 7.

The endo conformer has the lowest energy barrier, 3.98 KJmol^-1 lower than exo, making it the kinetic product. The chelotropic and unfavourable transition states' energies were significantly higher. The chelotropic has a high energy transition state because there are no possible stabilising orbital interactions as the sulphur dioxide approaches with the sulphur atom forward and oxygens facing away. The unfavourable endo and exo transition states have the highest energy. This is partly due to steric clashes with the xylylene molecule as sulphur dioxide approaches, resulting in destabilisation. The most significant factor is in fact the lack of aromaticity in the reaction. Conducting the Diels-Alder reaction with the dienophile site in the ring means that it can't be aromatised and lower the energy of the system like with the other three reactions. The unfavourable conformers show just how unstable xylylene is compared to the products that can be formed. Both endo conformers are lower in transition state energy than the exo ones because of the secondary orbital overlap taking place, as mentioned in exercise 2.

The unfavourable endo and exo products also have the highest product energies. The positive value in the relative energies reaction co-ordinate makes it less stable than the reactants. There is no spontaneous drive for the reaction as ∆G is positive. The high activation barrier and reaction energy makes these pathways kinetically and thermodynamically unfavourable. The chelotropic product has the lowest energy thereby making it the thermodynamic product. It is just over 50 KJmol^-1 more stable than the exo and endo products. Under reversible conditions, the chelotropic form would be the major product.

IRC pathways for o-Xylylene-SO2 Cycloaddition

Diels-Alder		Chelotropic
Exo	Endo
Unfavourable Exo	Unfavourable Endo

Conclusion

Computational chemistry gives great insight into the varying outcomes of one type of reaction such as Diels-Alder. The normal and inverse electron demand depends on the electronic nature of the components and ultimately results in different HOMO and LUMOs. These two contrasting orbital mixings are seen in the first and second reactions. Furthermore, the important transition state interactions such as secondary orbital overlap could be visualised and used to justify why the endo energy maximum was slightly lower than the exo in exercise 2. From extracting the final product energies, the thermodynamic product could be determined too, end in the case of exercise 2 as it was lower than exo. Finally, exploring the possible transition states gave results justifying why some were unfavourable and did not form, such as the ones formed in exercise 3 with positive ∆G. Aromaticity is a big driving force in exercise 3, lowering the energy of the products dramatically. It is vital to look beyond the diene and dienophile parts of molecules in the Diels-Alder reaction and consider all of the above in order to fully comprehend the data.