Rep:Mod:ts xl6813
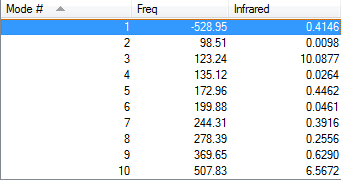
Introduction
Computation is very useful in studying the geometry of molecules and quantum chemical dynamics of the reaction because it can use mathematical method and chemistry theories to simulate reaction of molecules by computers. [1] In order to study the geometry and reactivity of cycloaddition, the Guassian 5.0 is used to determine the transition state, molecular orbitals involved in reaction and relative activation energy of cycloaddition reaction in following three cycloaddition. And the fundamental theory involved is potential energy surface (PES). It describes the energy of a molecule as a function of its geometry. [2]Because the energy of the transition state of the reaction is highest in a pathway, [2] so that the transition state shows as a saddle point with the value of the 1st derivative of energy 0 and the negative value of the 2nd derivative of energy. And the gradient of the transition state is zero in PES and energy decreases in both directions towards the reagents and the product. The reagents and the product usually shown as local minima [2]with the value of the 1st derivative of energy 0 and the positive value of the 2nd derivative of energy. And the energy from both the sum of reagents and the product increases towards the transition state.
In order to get correct transition state, there are two methods to check the geometry of the transition state of the reaction. One is the frequency calculation and the other is Intrinsic Reaction Coordination (IRC). In addition, In order to get more accurate energy and geometry of transition state, optimisation of molecule is very necessary. It helps to determine the local minimum in PES and result in a geometry with lowest energy, which gives a best geometry of the transition state. The job type for optimization of molecules is Opt.
The importance of Vibration Frequency
The job type for the vibration frequency is Freq and the vibration frequency determines the 2nd derivative of energy in terms of Cartesian-nuclear and mass-weighted coordinates. In order to get better result of the transition state, a combination job type Opt+Freq is used instead of Freq because it optimises the transition state to lowest stable energy. There is one negative vibration frequency for the transition state but all the vibration frequencies for reagents and products are positive.[1]
Nf710 (talk) 20:34, 7 February 2017 (UTC) You are saying a lot of things here and you arn't quite correct. vibrations frequencies are the derivative of energy in terms of a normal mode which is where you change the basis of coordinates in the molecules so that when you change the energy of the mode, it doesn't couple with any other mode (exchange energy) this is the coordinate of the vibration. secondly A TS only has one negative curvatures all the others are positive.
Intrinsic Reaction Coordination (IRC)
The job type for the intrinsic reaction coordination is IRC. It is used to determine energy changing in both directions from the transition state to check whether the transition state is correct with highest energy. While each point in IRC is optimised[1]
Diels-Alder cycloaddition
The Diels-Alder cycloaddition is a typical [4+2] cycloaddition which is the reaction occurs from the nucleophilic diene and the electrophilic dienophile. And then electrons are transferred from HOMO (highest occupied molecular orbital) of the diene to the LUMO (lowest occupied molecular orbital) of the dienophile. There are 6 πe-- involved in the reaction and 2πe-- from the electrophilic dienophile and 4πe-- from the nucleophilic diene.However, sometimes different substituents which are attaching to the diene and dienophile will revert the demand and result in nucleophilic dienophile and electrophilic diene. So that it is necessary to have a look at fragmental orbitals from 2 reagents to determine molecular orbital involved in the reaction.[3]
Exercise 1:Reaction of Butadiene with Ethylene
In order to get structure of the transition state of the reaction of butadiene with ethene, two reactants were optimized to a minimum without force constants and the method used in this time was PM6. After that two optimized reagents were replicated into a new panel to get a guess transition state by orienting butadiene and ethene in parallel and made the distance of neighboring terminal carbons in both reagents frozen 2.2 Å. And then this guess transition state was optimized to a minimum without force constants to make sure distances of the neighboring terminal carbons frozen. Subsequently this structure was optimized with job type Opt+Freq to a TS (Berny) and the force constants was once. And the result of this step was the transition state. The product was also optimized to a minimum without force constants to get a comparison with the transition state and reagents.
The structures of optimized the reagents, transition state and product are shown in the following Table 1.
| Table 1. Structures of optimised reactants and TS | |||
|---|---|---|---|
| Butadiene | Ethene | Transition State | Cyclohexene |
|
|
|
|
Two more steps were needed to determine the correctness of the structure of the transition state. First, checking whether there is only a negative frequency and then checking whether the animation of the negative frequency has correct vibration motion. Second, setting up a irc of the transition state to find out whether there is a saddle point.
The following Fig.1 is the result of frequency calculation for the cycloaddition reaction.
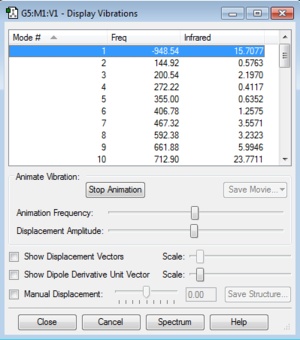
As Fig.1 shown, there is only one negative frequency so that the structure of the guessed transition state is reasonable. And then the animation of this negative frequency as following Fig.2 shown was checked.
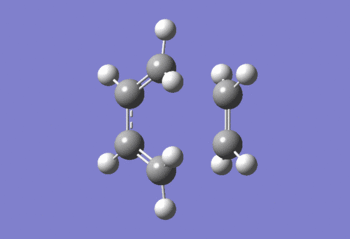
As Fig.2 shown, all C=C double bonds of the reagents are elongated and all C-C single bonds are shortened. So that the distances between the neighbouring terminal carbons of the two reagents are shortened so that new C-C single bonds can form to get the product cyclohexene. This proves that the guessed transition state is acceptable.
The result of irc for the reaction is shown in the following Fig.3.
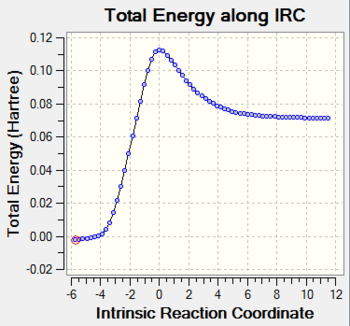
As Fig.3 shown, there is a saddle point which represents the transition state and the two local minimum represent the reagents and the product. This result makes the guessed transition state acceptable as well.
The left figure in the following Table 2 is the transition state of the reaction. All the carbons are hybridized between sp2 and sp3. Because the typical C-C bond is 1.54 Å and the typical C=C bond is 1.33 Å. [4]
The C-C bonds and C=C bonds are 1.41 Å and 1.38 Å in the transition state of the reaction. So that C-C bond shortened and the C=C bond elongated to form products cyclohexene. At first, the distances between the terminal carbons of the diene and their neighboring terminal carbons of the dienophile was set at 2.2 Å, but in the transition state, the distances shortened to 2.11 Å which is shorter than before and it is also shorter than twice of Van der Waal’s radius of carbon 1.7 Å. [5] It shows that the existence of p orbitals overlap between terminal carbons of the two reagents.
The middle figure and the right figure in the following Table 2 are negative vibration frequency and the first positive vibration frequency of the transition state. There are 6πe-- involving in the transition state. Due to the Woodward-Hoffmann rules, when the p orbital interactions between neighboring terminal carbons of two reagents in the transition state are one superfacial and one antarfacial, the reaction is thermally allowed. The transition state resembles the geometry of flat 6-membered ring. So that geometry of transition state with the negative vibration frequency has lower energy than that with positive vibration frequency. By comparison of the transition state vibration at these two different frequencies, the vibration with the negative frequency shortened the distances between the neighboring terminal carbons of two reagents and this mainly contributes to formation of the IRC of the reaction while the vibration with the positive frequency did not shorten the distances of two reagents.
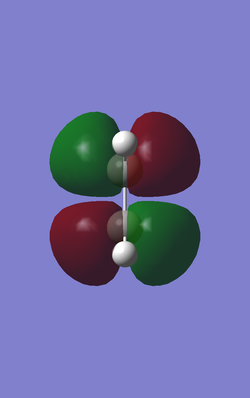
When determining which molecular orbitals of reagents participate the reaction both HOMO and LUMO of the reagents and the transition state are needed. The following Table 3 and table 4 are HOMO and LUMO of the reagents and the products.Butadiene has one anti-symmetric HOMO and one symmetric LUMO while the ethene has one symmetric HOMO and anti-symmetric LUMO. So that there are 2 possible interactions between the butadiene and the ethene. One is the interaction between anti-symmetric HOMO of the butadiene and anti-symmetric LUMO of the ethene. The other is the interaction between symmetric LUMO of the butadiene and symmetric HOMO of the ethene. Theoretically the diene should be nucleophilic and the dienophile should be electrophilic so that the interaction between anti-symmetric HOMO of the butadiene and anti-symmetric LUMO of the ethene is favorable and it obeys the mode of normal demand.
| Table 3. HOMO and LUMO of reagents butadiene and ethene | ||
|---|---|---|
| HOMO | LUMO | |
| cis-Butadiene | 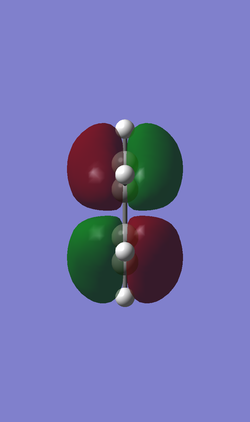
|

|
| Anti-symmetric (AS) | Symmetric (S) | |
| Ethene | 
|
|
| Symmetric (S) | Anti-symmetric (AS) | |
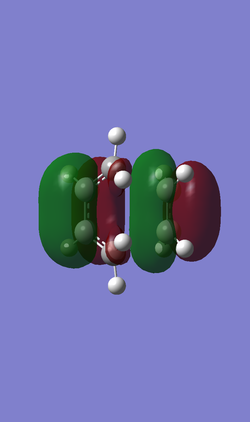
In the following Table 4, there are frontier orbitals of the transition state, both the HOMO and the LUMO orbitals of the transition state are symmetric. While the HOMO -1 orbital of the transition state is anti-symmetric. The LUMO orbital of the transition state is formed from symmetric LUMO of the butadiene and symmetric HOMO of the ethene. But the HOMO of the transition state is difficult to define by the HOMO and LUMO of the reagents in this case. The HOMO -1 orbital of the transition state seems to be formed from anti-symmetric HOMO of the butadiene and anti-symmetric LUMO of the ethene by appearance of the HOMO and LUMO of the reagents. And the energy difference between the HOMO -1 and the HOMO of the transition state is small. So that in this case the HOMO -1 should be the HOMO of the Diels-Alder cycloaddition reaction.
| Table 4. Frontier orbitals of cycloaddition TS PM6 | |||
|---|---|---|---|

|
|
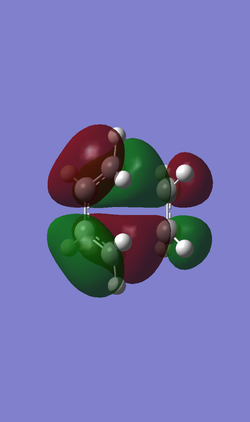
| |
| Orbital | LUMO | HOMO | HOMO-1 |
| Symmetry | S | S | AS |
| Relative energy | 0.01733 | -0.32533 | -0.32755 |
.
Nf710 (talk) 20:43, 7 February 2017 (UTC) This was a good section you put alot of effort into the organic theory, such as woodwood hoffman rules. You did however not do a MO diagram and you got a bit mixed up when talking about the energies of imaginary frequencies.
Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole
In order to get structure of the transition state of the reaction of cyclohexadiene and 1,3-Dioxole, two reactants were optimized to a minimum without force constants and the method used in this time was PM6.
After that two optimized reagents were replicated into a new panel to get a guess transition state by orienting cyclohexadiene and 1,3-Dioxole in parallel.
In order to get the geometry of the endo transition state, arranging the two sp2 carbons and the two oxygen atoms of the 1,3-Dioxole facing the four sp2 carbons of the cyclohexadiene so that the secondary orbital interaction between the p orbitals of the two oxygen atoms of the 1,3-Dioxole and their neighboring two sp2 carbons of the cyclohexadiene can stabilize the transition state. In order to get the geometry of the exo transition state, arranging the two sp2 carbons of the 1,3-Dioxole facing the two sp2 carbons of the cyclohexadiene and arranging the two oxygen atoms of the 1,3-Dioxole facing the two sp3 carbons of the cyclohexadiene. Moreover, the distances of the sp2 carbons of the 1,3-Dioxole and their neighboring sp2 carbons of cyclohexadiene were frozen at 2.2 Å.
And endo and exo transition state was optimized to a minimum without force constants to make sure distances of the neighboring carbons frozen. Subsequently these structure were optimized with job type Opt+Freq to a TS (Berny) and the force constants was once. And the result of this step was the transition state of endo and exo products. The products were also optimized to a minimum without force constants to get a comparison with the transition state and reagents.
The structures of optimized the reagents, transition state and product are shown in the following Table 5.
| Table 5. Structures of the optimised reagents, transition state and product via B3LYP/6-31G(d) | ||
|---|---|---|
| Cyclohexadiene | 1,3-Dioxole | |
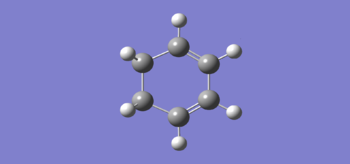
|
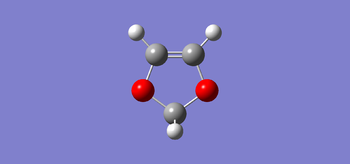
| |
| endo | exo | |
| transition state | 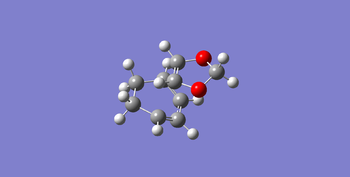
|
|
| product | 
|
|
The following Fig.4 is the result of frequency calculation for the endo cycloaddition reaction.
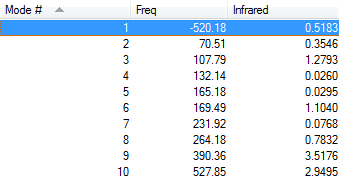
As Fig.4 shown, there is only one negative frequency so that the structure of the guessed transition state is reasonable. And then the animation of this negative frequency as following Table 6 shows that this transition state is reasonable.
The result of irc for the endo transition state is shown in the following Fig.5.
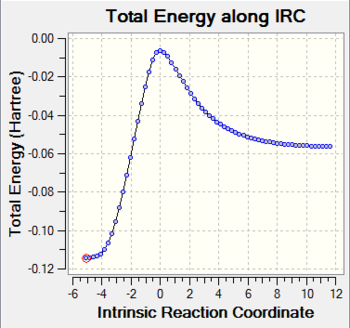
As Fig.5 shown, there is a saddle point which represents the transition state and the two local minimum represent the reagents and the product. This result makes the guessed transition state acceptable as well.
The following Fig.6 is the result of frequency calculation for the exo cycloaddition reaction.
As Fig.6 shown, there is only one negative frequency so that the structure of the guessed transition state is reasonable. And then the animation of this negative frequency as following Table 6 shows that this transition state is reasonable.
The result of irc for the exo transition state is shown in the following Fig.7.

As Fig.7 shown, there is a saddle point which represents the transition state and the two local minimum represent the reagents and the product. This result makes the guessed transition state acceptable as well. However, there is a weird point around the saddle point, there was the common Gaussian program error, which did not affect the result.
In the following Table 6, there are structures of the endo and exo transition states with some important bond length and also the vibrations of the endo and exo transition states. Both of the endo and exo products are formed via a 6_membered ring. So that all C=C bonds elongated and C-C bonds shortened in the transition states. And in the endo transition state, there are secondary orbitals overlap between p orbitals of oxygen in the 1,3-Dioxole and sp2 orbitals in the cyclohexadiene, which is favorable by stereoelectronic effect. While in the exo transition state, there is not stabilization of the transition state by secondary orbital interaction, so that the reaction is dominated by steric repulsion from the oxygen in the 1,3-Dioxole to the neighboring carbon in the cyclohexadiene, the separation of the two reagents in the exo transition state is larger than that in endo transition state.
| Table 6. Structures and vibrations of endo and exo TS | |||||
|---|---|---|---|---|---|
| Endo TS and bond lengths | Exo TS and bond lengths | ||||

|

| ||||
| Endo vibration at -520.18 cm-1 | Exo vibration at -528.95 cm-1 | ||||
Regioselectivity of endo and exo product in this Diels-Alder cycloaddition is results from different substituents attached to diene and dienophile. In this case, the dieophile is 1,3-Dioxole and the substituents attached to it are oxygen atoms so that p orbitals of oxygen atoms in the 1,3-Dioxole can overlap with another 2 sp2 carbons in the cyclohexadiene, as interaction of secondary orbitals, to give a more thermodynamically favorable endo product. Without the stabilization of this secondary orbital, it results in an exo product. Moreover, the substituents attached to the 1,3-Dioxole are electrowithdrawing groups which lower the energy of HOMO of 1,3-Dioxole, which makes dienophile nucleophilic and results in a inverse demand reaction.
("Without the stabilization of this secondary orbital, it results in an exo product." Do you know this for certain? Tam10 (talk) 12:36, 7 February 2017 (UTC))
The following Table 7 is about HOMO and LUMO of the reagents Cyclohexadiene has one anti-symmetric HOMO and one symmetric LUMO while the 1,3-Dioxole has one symmetric HOMO and anti-symmetric LUMO. There are 2 possible interactions between the cyclohexadiene and the 1,3-Dioxole. One is the interaction between anti-symmetric HOMO of the cyclohexadiene and anti-symmetric LUMO of the 1,3-Dioxole. The other is the interaction between symmetric LUMO of the cyclohexadiene and symmetric HOMO of the 1,3-Dioxole.
| Table 7. HOMO and LUMO of reagents cyclohexadiene and 1,3-Dioxole | ||
|---|---|---|
| HOMO | LUMO | |
| cyclohexadiene | 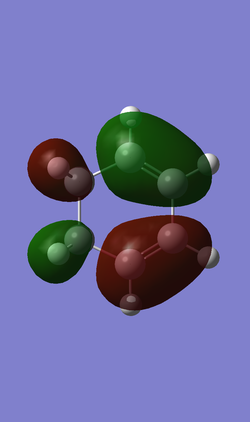
|
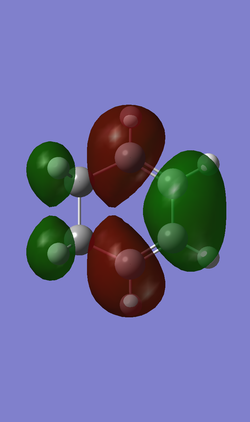
|
| Anti-symmetric (AS) | Symmetric (S) | |
| 1,3-Dioxole | 
|
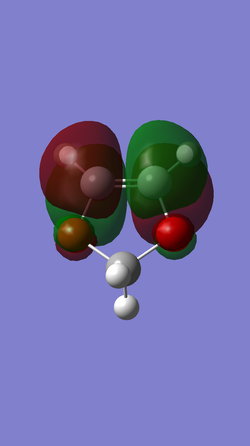
|
| Symmetric (S) | Anti-symmetric (AS) | |
In the following Table 8, there are HOMO frontier orbitals of the transition state in different views. By comparison of both side views of the HOMO of the transition state, there is not orbital forming between the oxygen atoms in the 1,3-Dioxole and sp2 carbons in the cyclohexadiene in the exo transition state. So that the electron density between the cyclohexadiene and the 1,3-Dioxole is lower in the exo transition state than that in the endo transition state. Consequently, the HOMO of endo transition state has a lower energy, due to presence of the secondary orbitals. Moreover, the HOMO of both the end and the exo transtion states are made from the HOMO of the 1,3-Dioxole and the LUMO of the cyclohexadiene. So that shows that 1,3-Dioxole is nucleophilic in this case, which proves the Diels-Alder cycloaddition reactions of the endo and the exo product are inverse demand of Diels-Alder cycloaddition.
| Table 8. Frontier orbitals of two TS | ||
|---|---|---|
| endo TS | exo TS | |
| HOMO | 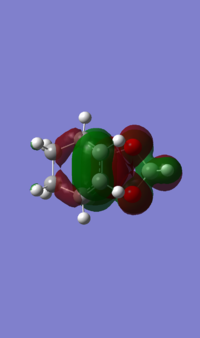 Front Front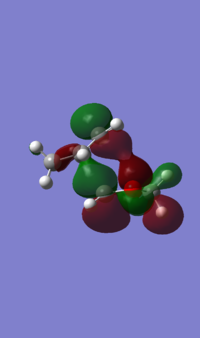 Side Side
|
 Front Front Side Side
|
(This does show the important differences between endo and exo, but it's still useful to show the formation of all 4 orbitals in each with an MO diagram Tam10 (talk) 12:36, 7 February 2017 (UTC))
The following Table 9 are summary of energy of reagents, transition state and products in the reaction from B3LYP/6-31G(d). By comparison of endo transition state and exo transition state, it shows that the Eendo TS is smaller than the < Eexo TS. Moreover, by comparison of endo product and exo product, it shows that the Eexo product is larger than < Eendo product. This is due to both stereoelectronic and steric effects. So that endo product is kinetic product due to lower Eactivation than that of exo reaction. While the exo product is thermodynamic product due to lower energy.
| Table 9. Summary of reaction energy via two TS | ||
|---|---|---|
| Energy term | B3LYP/6-31G(d) | |
| ECyclohexadiene + E1,3-Dioxole | -500.526097 a.u. | |
| Eendo TS | -500.332108 a.u. | |
| Eendo product | -500.577280 a.u. | |
| Eactivation of endo reaction | 0.193989 a.u.
(121.730 kcal mol-1) | |
| Eexo TS | -500.329168 a.u. | |
| Eexo product | -500.584880 a.u. | |
| Eactivation of exo reaction | 0.0196929 a.u.
(123.575 kcal mol-1) | |
Nf710 (talk) 20:53, 7 February 2017 (UTC) Your energies are incorrect and therefore you have come to the incorrect conclusion about the kenetic and thermo product. furthermore you said the oxygens are EWG and the reaction is therefore inverse. That would make it a normal demand reaction. Think about how the oxygens are bonded.
Exercise 3: Diels-Alder vs Cheletropic
In order to get transition states of the reaction between o-Xylylene and sulfur dioxide, both endo and exo products were optimized with the job type opt+freq to a minimum without force constants and the method used in this time was PM6. After optimization, vibration frequencies of the products were checked to ensure no presence of negative frequencies. And the optimized products were copied to a new panel. For the Diels-Alder reaction, the C-O and C-S bonds were disconnected and frozen about 2.0 Å. and 2.4 Å respectively. And the for the Cheletropic product, the 2 C-S bonds were disconnected and frozen at about 2.4 Å. The disconnected products were optimized to a minimum without force constants and the method used in this time was PM6. After making sure distances of the frozen bonds unchangeable, subsequently these structures were optimized with job type Opt+Freq to a TS (Berny) and the force constants was once. And the result of this step was the transition state of endo and exo products.
In the following Table 10, there are structures of the optimised transition states and the optimised products.
| Table 10. Structures of the optimised transition states and the optimised products via MP6 | ||
|---|---|---|
| endo | exo | |
| transition state | 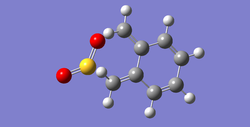
|

|
| product | 
|
|
(Your endo system is actually the exo, and what you've called exo is actually cheletropic. You're missing the endo DA reaction Tam10 (talk) 12:36, 7 February 2017 (UTC))
The following Fig.8 is the result of frequency calculation for the endo cycloaddition reaction.
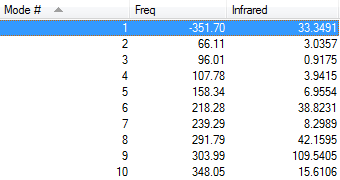
As Fig.8 shown, there is only one negative frequency so that the structure of the guessed transition state is reasonable. And then the animation of this negative frequency as following Table 11 shows that this transition state is reasonable.
The result of irc for the endo transition state is shown in the following Fig.9.
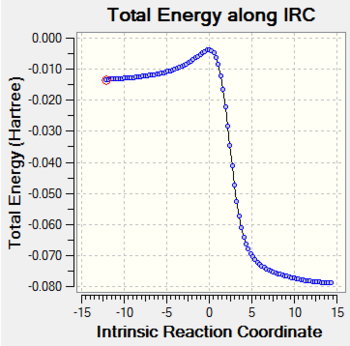
As Fig.9 shown, there is a saddle point which represents the transition state and the two local minimum represent the reagents and the product. This result makes the guessed transition state acceptable as well.
The following Fig.10 is the result of frequency calculation for the endo cycloaddition reaction.
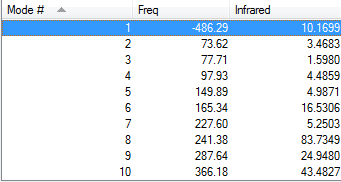
As Fig.10 shown, there is only one negative frequency so that the structure of the guessed transition state is reasonable. And then the animation of this negative frequency as following Table 11 shows that this transition state is reasonable.
The result of irc for the endo transition state is shown in the following Fig.11.
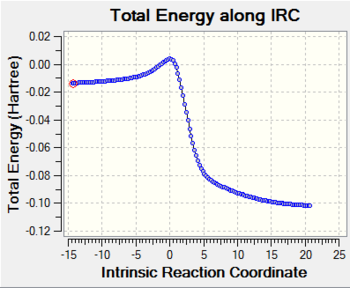
As Fig.11 shown, there is a saddle point which represents the transition state and the two local minimum represent the reagents and the product. This result makes the guessed transition state acceptable as well.
The following Table 11 is about the structures and irc animation of endo and exo TS.
Regioselectivity of endo and exo product in this cycloaddition is results from different functional group of sulfur dioxide reacting with the terminal diene of o-xylylene. From the irc animations of both endo and exo transition state, some geometry information of transition states can be given as following. For the endo product formation, the transition state formed via a distorted 6-membered ring due to the two heteroatoms sulfur and oxygen. While for the formation of exo production, the transition state occurred via a symmetric 5-membered ring. In order to form transition state, all C=C bonds in the formed ring elongated while the C-C bond in the formed ring shortened. Moreover, delocalization of πe-- of the o-xylylene decreased from 8πe-- to 6πe--, which raised the energy of the transition state. So that the other 6-membered ring of the o-xylylene become planar and all carbons in the ring is sp2 and all carbon carbon bonds are equal.
| Table 11. Structures and irc animation of endo and exo TS | |||||
|---|---|---|---|---|---|
| Endo TS and bond lengths | Exo TS and bond lengths | ||||

|

| ||||
| irc of Endo transition state | irc of Exo transition state | ||||
The following Table 12 are summary of energy of reagents, transition state and products in the reaction from PM6. By comparison of endo transition state and exo transition state, it shows that the Eendo TS is smaller than the < Eexo TS. Moreover, by comparison of endo product and exo product, it shows that the Eexo product is larger than < Eendo product. This is due to steric effect. So that endo product is kinetic product due to lower Eactivation than that of exo reaction. While the exo product is thermodynamic product due to lower energy.
| Table 12. Summary of reaction energy via two TS | |
|---|---|
| Energy term | MP6 |
| Eo-Xylylene + Esulfur dioxide | -0.009210 a.u. |
| Eendo TS | 0.092077 a.u. |
| Eendo product | -0.078968 a.u. |
| Eactivation of endo reaction | 0.101287 a.u.(63.5586 kcal mol-1) |
| Eexo TS | 0.099060 a.u. |
| Eexo product | -0.900005 a.u. |
| Eactivation of exo reaction | 0.108270 a.u.(67.9404 kcal mol-1) |
In the following Fig.12, it shows the energy profile of both endo Diel-Alder reaction in plain line and exo Cheletropic reaction in dashed line.
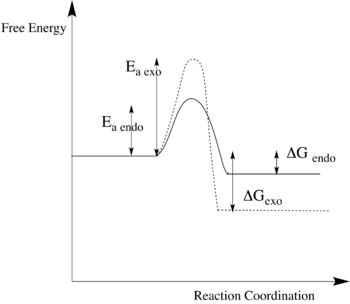
Further Work
In the following Table 13, it shows that structures of TS for the reaction occuring in the other diene of o-Xylylene and the sulfur dioxide.
| Table 13. Structures of endo and exo TS for the reaction occuring in the other diene of o-Xylylene and the sulfur dioxide | |||||
|---|---|---|---|---|---|
In the following Table 14, it shows that summary of reaction energy via two TS for the reaction occuring in the other diene of o-Xylylene and the sulfur dioxide.
| Table 14. Summary of reaction energy via two TS for the reaction occuring in the other diene of o-Xylylene and the sulfur dioxide | |
|---|---|
| Energy term | MP6 |
| Eo-Xylylene + Esulfur dioxide | -0.009210 a.u. |
| Eendo TS | 0.102070 a.u. |
| Eendo product | 0.065612 a.u. |
| Eactivation of endo reaction | 0.111280 a.u.(69.8293 kcal mol-1) |
| Eexo TS | 0.113006 a.u. |
| Eexo product | 0.045612 a.u. |
| Eactivation of exo reaction | 0.122216 a.u.(76.6917 kcal mol-1) |
By comparison of these four endo products and exo products, the Eendo TS and the Eexo TS in this case are higher than those of Eendo TS and the Eexo TS in the precious reaction. And also Eendo product and the Eexo productin this case are higher than those of Eendo TS and the Eexo TS in the precious reaction. So that it makes the endo and exo products of the reaction occurs between sulfur dioxide and the diene in the ring of the o-Xylylene less kinetic favorable and less thermodynamic favorable than the reaction between sulfur dioxide and the diene in the terminal part of the o-Xylylene.
Conclusion
By using Gaussian with method B3LYP/6-31G(d) and PM6, the geometry of transition state of three different kinds of cycloaddition can be determined. While B3LYP/6-31G(d) can give a more accurate geometry but longer time to run the reaction. Both vibration frequency calculation with job type opt+freq and irc can check the correctness of the geometry of the transition state. The three cycloadditions are studied by energy optimisation, MO analysis and geometry of the transition states. The main study of the butadiene and the ethene is MO analyzation of frontial orbitals of HOMO and LUMO from the HOMO and LUMO of the reagents fragment to show a normal demand of nucleophilic diene reacting with electrophilic dienophile. Another two reactions are focused on the regioselectivity of endo and exo product while the reaction of cyclohexadiene and 1,3-dioxole shows an inverse demand of Diels-Alder reaction. Another two reactions are focused on kinetic and thermodynamic selectivity of products by determining energy of the reagents, the transition states and the products.
Reference
- ↑ 1.0 1.1 1.2 Gaussian 03 Revision, M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, Jr., etc, Gaussian, Inc., Wallingford CT, 2004.
- ↑ 2.0 2.1 2.2 E.G.Lewars, Computational Chemistry, 2th Ed,Netherland, 2003, 9-43, DOI 10.1007/978-90-481-3862-3
- ↑ Carey, Francis A., Richard J., Adv. Org. Chem. 5th Ed, New York, 2007, 836–850 ISBN 0387448993
- ↑ Marye A., James K. Organische Chemie: Grundlagen, Mechanismen, Bioorganische Anwendungen Springer, 1995 ISBN 978-3-86025-249-9
- ↑ Bondi A., J. Phys. Chem., 1964, 68, 441-451 doi:10.1021/j100785a001