Rep:Mod:ts ew515
Introduction
Presented here is a computational modelling of various pericyclic reactions using semi-empirical and Density Functional Theory (DFT) methods in the software Gaussian. Within each exercise, the program will be used to do such things as: describe/visualize relevant molecular orbitals and their symmetries, monitor the geometric development of a reaction, and calculate reaction and activation energies to differentiate between kinetic and thermodynamic pathways.
Gaussian
The computational methods in Gaussian rely on several assumptions to allow the N-body Schrodinger equation to be approximated. To begin with, the Born-Oppenheimer approximation notes the vast difference in kinetic energies between nuclei and electrons to provide its assumption that their motions can be separated from one another, i.e. the N-body wave-function can be separated into an electronic portion (dependent on nuclear position, not motion, and treated quantum mechanically) and a nuclear one (treated classically). Additionally, the total electronic wave-function is decomposed into single-electron wave-functions that are derived from atom-centered functions (the basis set) via a linear combination of atomic orbitals (LCAO). Finally, the energetic element of electron-electron repulsion is not calculated discretely between each and every electron in the system. Instead, the approximate single-electron wave-functions are treated independently and exposed to an averaged repulsive field of the other electrons in the system.
Methods/Levels of Theory
The simplest type of ab initio method (computing properties from first principles, i.e. the electronic Schrodinger equations) is the Hartree-Fock (HF) method, which approaches the N-body quantum system via the approximations described above. One of the essential differences between HF theory and following ab initio approaches is the mathematical approach to approximating electron-electron repulsions.
In a more computationally-intensive fashion than HF, Density Functional Theory includes an approximation of instantaneous electron-electron repulsions (or, as a whole, an approximation of correlated electron motion) by introducing an exchange-correlation potential in energy calculations instead of an averaged repulsive field. There are a variety of specific approaches to handling the computation of electron exchange and correlation energies. In this work, a "hybrid functional" known as B3LYP is used. Additionally, DFT computes energies directly from the electron density, instead of by an operation on the approximate wave-function.
Finally, semi-empirical methods, such as PM6, use a combination of both quantum mechanical calculation and parameterized empirical data to yield less accurate but faster modelling than given by the above theories.
The Potential Energy Surface
In the context of analyzing a reaction, Gaussian will not only use the above methods to geometrically optimize reactants and products, but also to identify the relevant transition states lying along their interconversion. The underlying component that unifies the procedure of identifying these states is the potential energy surface (PES). As an idea, the PES represents the molecular energy as a function of molecular geometry. If presented as a three-dimensional plot, the vertical axis would represent potential energy, while the horizontal axes would represent reduced coordinates that correspond to some or all of the fundamental geometric degrees of freedom in the system (i.e. the 3N-6 normal modes for a nonlinear molecule).
With this idea in mind, an energetic topology can be envisioned with minima, maxima, and saddle points depending on the relative configuration of atoms in the molecule or system. When carrying out minima/maxima/transition state optimizations, Gaussian will use the topology gradient (first derivative of energy with respect to geometric change, dE) and curvature (second derivative, d2E) to differentiate between these features. All three of these features are similar in that they are "flat points" with a gradient of 0 with respect to geometric change. Individually, minima have a positive curvature (increase in energy) in every direction and maxima have a negative curvature (decrease in energy) in every direction. As transition states are the highest energy point along the lowest energy pathway, it follows that transition states have positive curvatures in every direction except for one negative curvature along a particular geometric degree of freedom (the direction of the reaction that goes "down" to both reactants and products).
These curvatures are measured by Gaussian as vibrational frequencies. In simple terms, molecular vibrations occur along some geometric coordinate and the energy is either raised (a positive frequency, seen experimentally) or lowered (a negative frequency, imaginary). Thus, a frequency analysis is used to confirm an optimized minima by checking for no imaginary vibrations (a stable point with positive curvature), while an optimized TS is expected to show one imaginary vibration (a saddle point with a negative curvature along one geometric degree of freedom, the reaction pathway).
Nf710 (talk) 17:39, 9 March 2018 (UTC) The way guassian does this is it diagonalises the hessian matrix and the eigen values are the force constants and the eigenvectors are the normal modes which are linear combinations of the degrees of freedom. moving back and forth along these vectors looks like a vibration.
Nf710 (talk) 17:31, 9 March 2018 (UTC) This is really well written section. It would have been great if you could have included something on Basis sets or some equations...
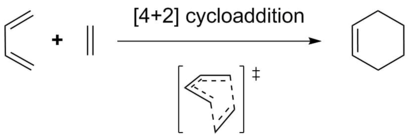
Exercise 1: The Diels-Alder Reaction of Butadiene with Ethylene
(Fv611 (talk) Good exercise overall, but you missed out on some key elements of the discussion (mainly orbital overlap requirements in general, and the bond formation mechanism). Additionally, you did not optimise butadiene to its true minimum, leading to the wrong relative placement of its orbitals.)
Using the semi-empirical PM6 method: 1) The butadiene and ethylene reactants were optimized independently, 2) a fixed-geometry pseudo-TS was minimized, 3) the pseudo-TS was unfrozen and optimized to a true transition state structure, 4) the optimized TS was used to run an intrinsic reaction coordinate (IRC) calculation to approximate the minimum energy pathway between reactants and products, and 5) the cyclohexene product was geometrically optimized.
Frontier Molecular Orbital (FMO) Analysis

The Diels-Alder reaction of butadiene with ethylene is a concerted [4+2] cycloaddition. The reaction can be considered by the HOMO/LUMO interactions of the reactants (Fig. 1). Frontier molecular orbitals were annotated as symmetric or antisymmetric with respect to orbital phases at reactant termini.
Per the Woodward-Hoffman (WF) rules (N + A = odd, where N is the number of electron pairs and A is the number of antarafacial components), the [4+2] cycloaddition is thermally achievable via a suprafacial/suprafacial interaction of reactants (as seen in the simplified reaction scheme TS). This was confirmed by the MO analysis of the reactants and transition state.
The relevant molecular orbitals that comprise the FMO manifold are the HOMO/LUMO pairs of each reactant. As summarized by the WF rules, the antisymmetric butadiene HOMO is able to interact with the antisymmetric ethylene LUMO to yield a non-zero orbital overlap while the symmetric ethylene HOMO can do the same with the symmetric butadiene LUMO. In the case of pericyclic reactions with an even number of electron pairs, a hypothetical suprafacial/suprafacial interaction would yield unproductive symmetric/antisymmetric interactions (with an orbital overlap integral of zero). Instead a thermally-promoted reaction would be required to pass through a suprafacial/antarafacial interaction to achieve any productive orbital overlap.
MO energies and visualizations for the reactants were taken from the first frame of the intrinsic reaction coordinate calculation (see next section) of the system, instead of the independently optimized reactants, while transition state MOs were taken from the optimized transition state calculation.
| Butadiene MOs | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
MO #17 (HOMO, antisymmetric) |
MO #18 (LUMO, symmetric) | ||||||||||
| Ethene MOs | |||||||||||
MO #16 (HOMO, symmetric) |
MO #19 (LUMO, antisymmetric) | ||||||||||
| Transition State MOs | |||||||||||
MO #16 butadiene HOMO + ethene LUMO (in phase a/a overlap) |
> MO #17 butadiene LUMO + ethene HOMO (in phase s/s overlap) |
MO #18 butadiene LUMO + ethene HOMO (out of phase s/s overlap} |
MO #19 butadiene HOMO + ethene LUMO (out of phase a/a overlap) | ||||||||
Intrinsic Reaction Coordinate Analysis & C-C Bond Length Development

A comparison between the imaginary vibration used to confirm an appropriate transition structure (Fig. 2a) and the entire animation of interconverting geometries along the IRC (Fig. 2b) illustrates the discussion about PES topology/curvatures from the previous section.
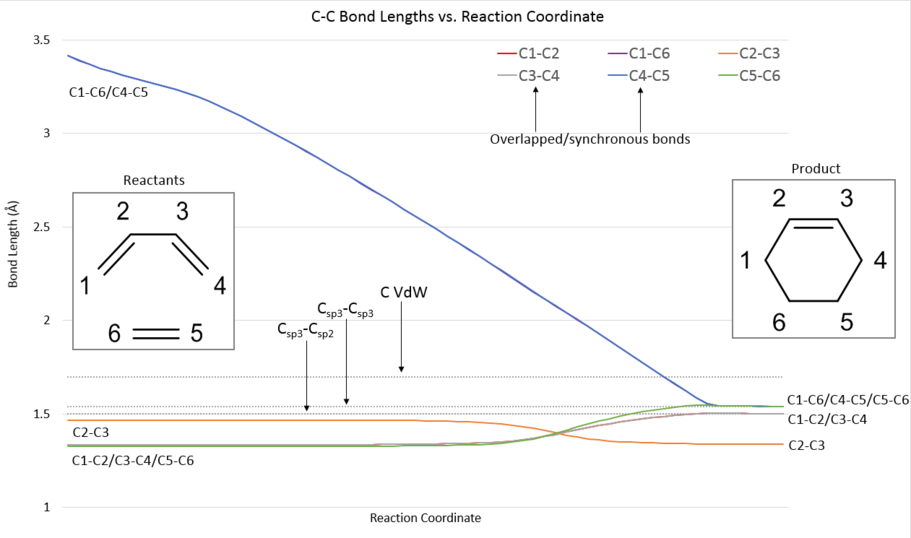
The IRC analysis of the reaction system, starting from the optimized transition state, was used to plot the development of carbon-carbon bond lengths as the reaction proceeds (Fig. 3). Relevant lengths are plotted in color, while standard sp3-sp3 (1.54 angstroms) and sp3-sp2 (1.50 angstroms) lengths, as well as carbon's Van der Waals radius (1.70 angstroms), are plotted as grey dotted lines.
Bond lengths change as would be expected:
- Pi bonds in the reactants form sigma bonds and increase in length, however, the resulting sp3-sp3 bond (C5-C6) is longer (1.54 angstroms, as standard) than the resulting sp3-sp2 bonds (C1-C2/C3-C4) which match the standard length of 1.50 angstroms
- The two new sigma bonds formed in the reaction (C4-C5/C1-C6) gradually decrease in length from arbitrarily higher values until settling on the standard sp3-sp3 length (1.54) with C5-C6
- Finally, the newly formed pi bond (an sp2-sp2 sigma bond in the reactants at 1.47 angstroms) decreases in length to 1.34 angstroms

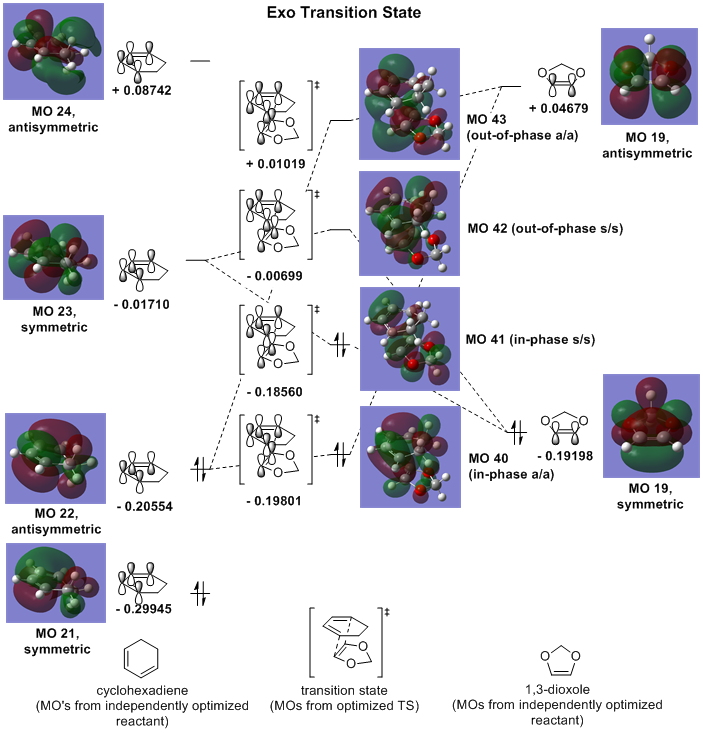
Exercise 2: The Diels-Alder Reaction of Cyclohexadiene with 1,3-Dioxole
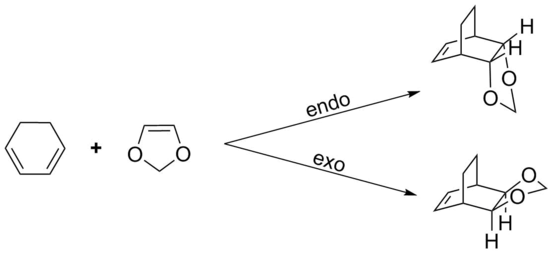
Using firstly the PM6 method followed by a DFT (B3LYP) calculation: the cyclohexadiene and 1,3-dioxole reactants were optimized independently, 2) a fixed-geometry pseudo-TS was minimized for both endo and exo interactions, 3) both were unfrozen and optimized to a true transition state, 4) the transition structures were used to run an IRC calculation (only PM6), and 5) the endo/exo products of the IRC were optimized.
Frontier Molecular Orbital (FMO) Analysis
(Fv611 (talk) You provide the same MO with different energy values. You should have discussed more the difference between the endo and exo conformations in terms of their relative MO energies.)
In a similar fashion to exercise 1, this [4+2] cycloaddition can also be considered via the HOMO/LUMO overlap of each reactant. Again, the optimized transition state showed a thermally-accessible suprafacial/suprafacial interaction in the cycloaddition. Antisymmetric/antisymmetric and symmetric/symmetric interactions between reactants yielded non-zero orbital overlaps (to give bonding/antibonding FMOs in the transition state) as before.
Interestingly, there is a reordering of reactant HOMOs. Instead of an electron-rich diene reacting with a relatively electron-poor dienophile (higher energy butadiene HOMO relative to ethene HOMO, Fig. 1), cyclohexadiene's reaction with 1,3-dioxole actually demonstrates an inverse demand Diels-Alder reaction, wherein the electron-rich dioxole (the dienophile) HOMO lies higher in energy than that of cyclohexadiene (the diene).
Between the endo and exo transition structures, there is a notable difference in the energies and orbital overlap of either HOMO (MO #41):
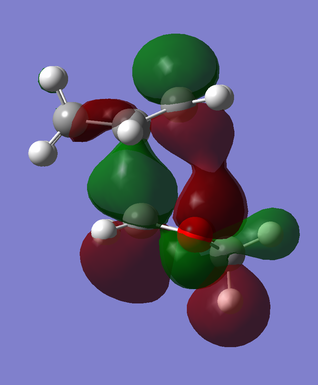
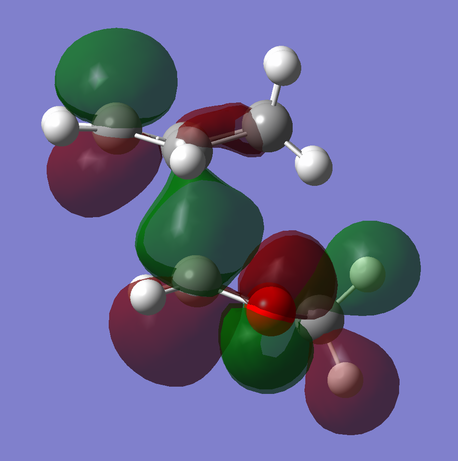
The termini of the reacting pi systems overlap to yield primary orbital interactions (present in both endo and exo transition states) that lead the system to undergoing a cycloaddition (as described previously in reference to the WH rules). Uniquely, the endo transition state offers an additional stabilizing feature over that of the exo TS: secondary orbital overlap -- an overlap of orbital density on the dioxole oxygen atoms with that on the unsaturated carbon atoms of the cyclohexadiene (Fig. 6, primary overlap in green/secondary overlap in red). The lack of any additional orbital interaction is distinctly seen in the HOMO of the exo transition state (Fig. 7).
Nf710 (talk) 17:45, 9 March 2018 (UTC) What you have said about the electron demand of the reaction is in theory correct. but you have investigated it quantitively. You could have done this with a single point energy on the first point of the reactants on the IRC
Thermochemistry
| Endo | Exo | |||
|---|---|---|---|---|
| Hartrees | kJ/mol | Hartrees | kJ/mol | |
| Activation Barrier | 0.059703 | 156.750238 | 0.062689 | 164.589982 |
| Reaction Energy | -0.026838 | -70.46317437 | -0.025469 | -66.86886459 |
The thermochemical data from the optimized reactants, transitions states, and products were used to tabulate activation barriers and overall reaction energies for both the endo and exo reactions above. The data show each pathway to have a moderate reaction barrier, while each is exothermic overall.
The endo TS has a lower activation barrier than the exo, meaning it is the kinetically preferred (faster formed) pathway as is expected in Diels-Alder reactions. This may be explained by he FMO analysis described previously in which both TS's were seen to satisfy the WF rules (allowing primary orbital overlap) but the endo TS had additional secondary orbital overlap in the HOMO to further stabilize it.
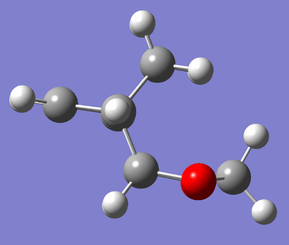
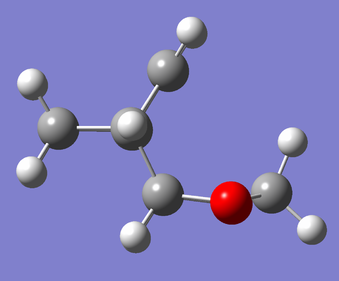
Interestingly, the data also show that the endo product is thermodynamically favored, with the endo reaction contributing around an extra -3.5 kJ/mol to the reaction energy compared to the exo pathway. This might not be in agreement with a first guess (i.e. any endo/exo rule of thumb), however it can be attributed to the relative steric interactions in the exo (Fig. 8) and endo (Fig. 9) products. In the exo product there are unfavorable interactions between the saturated ethylene bridge of the cyclohexene unit (pictured pointing up) with the methylene portion of the dioxole unit (pictured pointing right) that are not present in the endo product (in which the methylene unit of dioxole is endo to the saturated portion of the ring and better tolerated spatially).
Nf710 (talk) 17:56, 9 March 2018 (UTC) Tis was a nicely wirtten section. You could have gone into more detail about the electron demand. And also for some of the theory for kenetics and thermodynamics. But overall a good section.
Exercise 3: The Diels-Alder and Cheletropic Reactions of ortho-Xylylene with Sulfur Dioxide
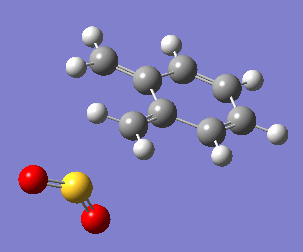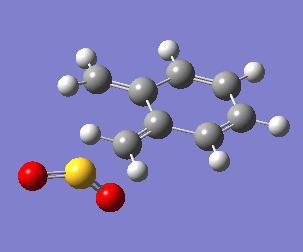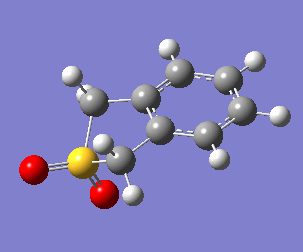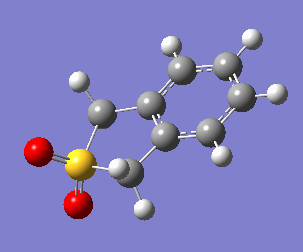
Uniquely, between the o-xylylene and SO2 reactants, there are two reactions available to them: a Diels-Alder cycloaddition(forming both endo, Fig. 10a, and exo, Fig. 10b, products), or a cheletropic cycloaddition (Fig. 10c).
 |
 |
 |
|---|
The thermochemical data from these reaction calculations were tabulated from the individually optimized reactants (i.e. at infinite separation), the optimized transition states, and respective products:
| Diels-Alder | Cheletropic | |||||
|---|---|---|---|---|---|---|
| Endo | Exo | |||||
| Hartrees | kJ/mol | Hartrees | kJ/mol | Hartrees | kJ/mol | |
| Activation Barrier | 0.030927 | 81.1988447 | 0.032446 | 85.1869795 | 0.039428 | 103.518222 |
| Reaction Energy | -0.037936 | -99.60097559 | -0.038178 | -100.2363466 | -0.059635 | -156.5717044 |
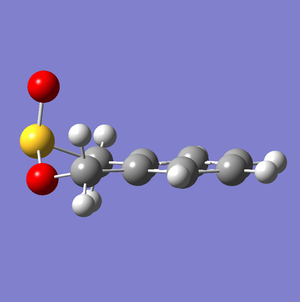
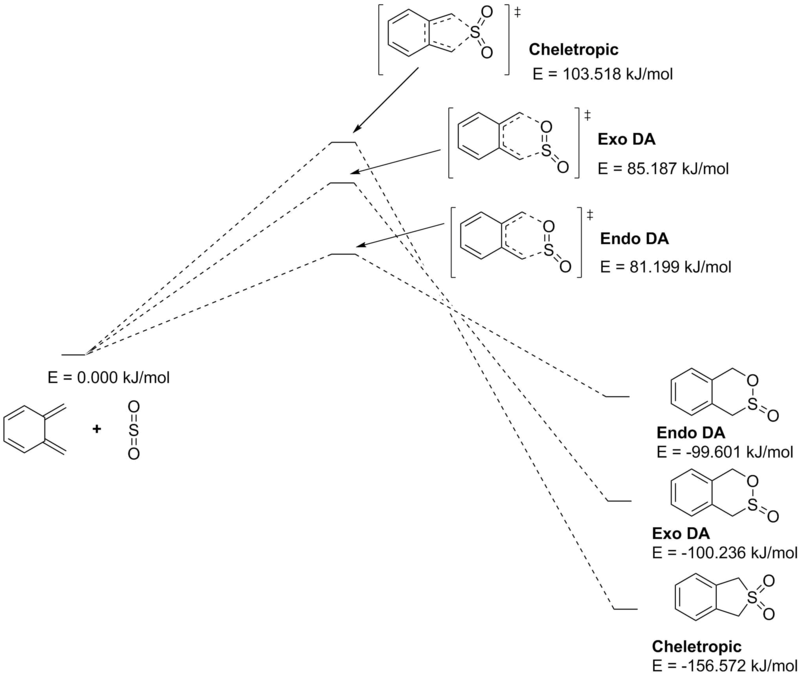
Between the three of them, the cheletropic is hugely more thermodynamically favorable with an almost 50% increase in exothermicity. Interestingly, the cheletropic reaction also provided the largest reaction barrier, significantly above those of each Diels-Alder pathway.
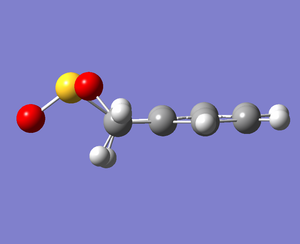
Between the Diels-Alder products, the endo TS was relatively lower in energy (the kinetically favorable process) while the exo product was more favorable (the thermodynamically preferred pathway). All energy levels for each of these reactions are depicted in Fig. 12.
| Cheletropic | Diels-Alder (Endo) | Diels-Alder (Exo) |
|---|---|---|

|
|
|
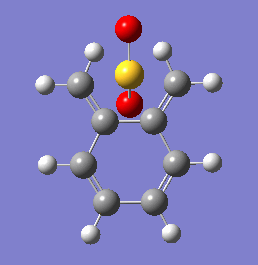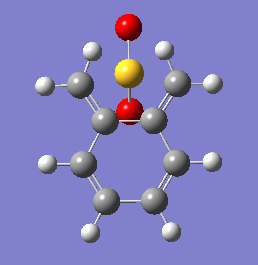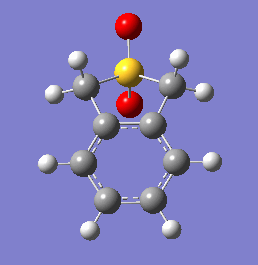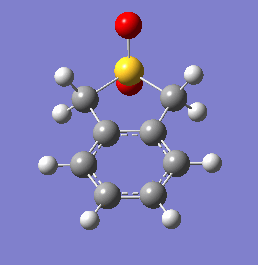
These energetic differences can be considered by the steric interactions present in the respective products. The cheletropic product adopts a planar and symmetric conformation with minimal interactions between the bulky oxygen atoms and adjacent hydrogens. Alternatively, the endo DA product shows a significantly more unfavorable orientation of the saturated ring hydrogens and external oxygen (situated axially) that is akin to a 1,3 diaxial type interaction. The exo product has its external oxygen atom situated equatorially preventing such a steric clash.
(There is also the retention of both S=O bonds in the cheletropic product. The sulfur is too large to form a planar 6-membered ring Tam10 (talk) 13:35, 7 March 2018 (UTC))
One of the most obvious features driving the exothermicity of these reactions is the formation of an aromatic product. The reactive and unstable xylylene reactant is non-aromatic but disposed to rearrange quickly to recover aromaticity (Fig. 11). It is likely that the formation of aromaticity occurs early in the reaction coordinate.
All Gaussian files can be found here: File:Ew515 Exercise1 LOGFiles.zip, File:Ew515 Exercise2 LOGFiles.zip, File:Ew515 Exercise3 LOGFiles.zip
References
1 Computational Quantum Chemistry: Molecular Structure and Properties in Silico, ed. nonymous , The Royal Society of Chemistry, 2013, p. 1-62.
2 A. Szabo and N. S. Ostlund, Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory, Dover Publications, 1989.