Rep:Mod:ts cyy113 edit

Species or IRC	Basis Set
Species or IRC	PM6
o-xylylene	File:Xylene cyy113.log
SO₂	File:SO2 CYY113.LOG
Endo TS	File:EX3ENDOTS CYY113.LOG
Exo TS	File:XYLYLENE exoex3 TS cyy113.LOG
Cheletropic TS	File:INDENE TS cyy113.LOG
Endo Product	File:ENDOPRODUCT cyy113ex3.LOG
Exo Product	File:EXOPRODUCT OPT CYY113.LOG
Cheletropic Product	File:INDENEPRODUCT CYY113.LOG
Endo IRC	File:EX3ENDOTSIRC cyy113.LOG
Exo IRC	File:Xylene exo ts irccyy113.log
Cheletropic IRC	File:INDENEIRC CYY113.LOG

**Table X: Energies of the reactants, TS and products in the alternative reaction between o-xylylene and SO₂**
Xylylene		SO₂		Endo TS
Energy (Hartrees)	Energy (kJ mol^-1)	Energy (Hartrees)	Energy (kJ mol^-1)	Energy (Hartrees)	Energy (kJ mol^-1)
0.178746	469.297659	-0.118614	-311.4210807	0.102070	267.98480541
Endo Product		Exo TS		Exo Product
Energy (Hartrees)	Energy (kJ mol^-1)	Energy (Hartrees)	Energy (kJ mol^-1)	Energy (Hartrees)	Energy (kJ mol^-1)
0.065609	172.25644262	0.105054	275.81929801	0.067306	176.711916

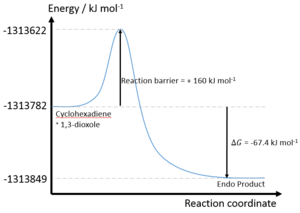
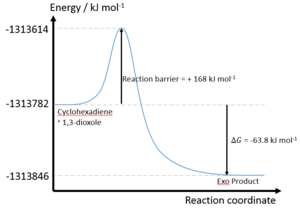
Reaction	Formation of Endo Product	Formation of Exo Product
Reaction barrier/ kJ mol^-1	+110.1	+117.9
Reaction energy/ kJ mol^-1	+14.4	+18.8

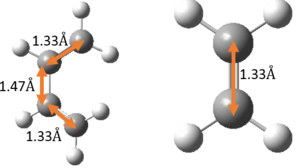
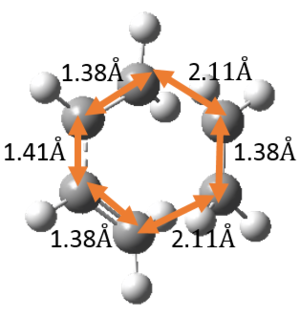
The relevant C-C bond lengths are tabulated below:

Table 2
Reactant C-C bond lengths	TS C-C bond lengths	Product C-C bond lengths

Reported sp² and sp³bond lengths in cyclohexene^[1] /Å	Typical sp² and sp³ bond lengths^[2] /Å	Van Der Waals' radius of C atom^[3] /Å
	sp² = 1.31-1.34 sp³ = 1.53-1.55	0.77

Write whether the orbital overlap integral is zero or non-zero for the case of a symmetric-antisymmetric interaction, a symmetric-symmetric interaction and an antisymmetric-antisymmetric interaction.

The orbital overlap integral $S$ quantifies the extent of overlap between reactant MOs (denoted by $ψ_{1}$ and $ψ_{2}^{*}$ . It is given by the following equation.^[4]

S = \int ψ_{1} ψ_{2}^{*} d τ

Equation 2: Equation of the overlap integral

The possible values of $S$ depends on $ψ_{1}$ and $ψ_{2}^{*}$ and they are as follows:

Type of interaction	Symmetric-Antisymmetric	Symmetric-Symmetric	Antisymmetric-Antisymmetric
Value of S	Zero	Non-Zero	Non-Zero

intro

In your introduction, briefly describe what is meant by a minimum and transition state in the context of a potential energy surface. What is the gradient and the curvature at each of these points? (for thought later on, how would a frequency calculation confirm a structure is at either of these points?)

The dynamics of a chemical reaction can be investigated using a potential energy surface (PES) obtained by plotting $V (q_{1}, q_{2})$ against $q_{1}$ and $q_{2}$ , where $V (q_{1}, q_{2})$ is the potential energy and $q_{1}$ , $q_{2}$ are order parameters of a reaction. Reactants and products occur at the minimum of the PES while transition states occur at the saddle point. Mathematically, they are both stationary points, so the gradient (i.e. the first derivative $\partial V / \partial q_{i}$ ) of both the minimum and the saddle point is 0. However, the curvature of the minimum is concave while that of the saddle point is convex. Thus, they can only be distinguished by taking the second derivative $\partial^{2} V / \partial q_{i}^{2}$ , which will be positive for the minimum, but negative for the saddle point.

Since a chemical bond can be modelled as a spring, Hooke's Law (eq. 1) can be invoked, where $V$ is the elastic potential energy, $k$ is a constant and $x$ is the displacement of the particle from its equilibrium position.

V = 1 / 2 k x^{2}

Equation 1: Hooke's Law

Taking the second derivative of this equation results in eq. 2. Thus, $k$ will be positive for all minimum points but negative for saddle points. Physically, this means that all coordinates have been minimised for reactants and products, but some coordinates have not been minimised for transition states. Thus, reactants and products remain stable unless they are excited with energy but transition states are inherently unstable and will rearrange into a stable form spontaneously.

\partial^{2} V / \partial x^{2} = k

Equation 2: Second derivative of Hooke's Law

Since the vibrational frequency $ω$ is a function of $\sqrt{k}$ (eq. 3), reactants and products will always give real frequencies, while transition states will give imaginary frequencies. A well-chosen reaction coordinate will only result in a transition state with one imaginary frequency, as all other coordinates have been minimised.

ω = 1 / 2 π \sqrt{k / m}

Equation 3: Relation between frequency and $k$

In these exercises, computational methods were used to determine suitable reaction coordinates of several [4+2] Diels-Alder cycloadditions. The coordinates of the reactants, transition state (TS) and products were optimised using Gaussian, from which an Intrinsic Reaction Coordinate (IRC) calculation was run to visualise the approach trajectory of the reactants to form a transition state and subsequently the product. Further observable parameters (Bond Length and Energies) were also analysed from the optimised coordinates and IRC calculation. The wavefunctions of the optimised species were visualised as molecular orbitals (MOs) and their shapes and symmetries were compared to theoretical predictions.

Optimisation was conducted at the semi-empirical PM6 level first, before some calculations were refined using Density Functional Theory (DFT) methods at the BY3LP/6-31(d) level. The PM6 optimisation uses a fitted method drawing on experimental data, hence it is less accurate. However, it saves computational resources and is a good starting point for initial calculations. The BY3LYP/6-31(d) optimisation is more accurate but it comes at the cost of computational effort.

Formation of endo product	Formation of exo product
(A): Energy profile of the endo product formation	(B): Energy profile of the exo product formation
Fig. Y: Energy profile diagrams showing the reaction barrier and reaction energies of the reaction

MO Analysis

Using your MO diagram for the Diels-Alder reaction, locate the occupied and unoccupied orbitals associated with the DA reaction for both TSs by symmetry. Find the relevant MOs and add them to your wiki (at an appropriate angle to show symmetry). Construct a new MO diagram using these new orbitals, adjusting energy levels as necessary.

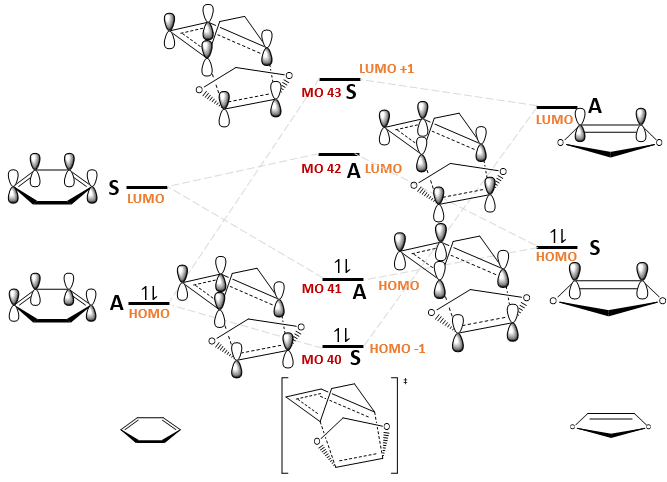
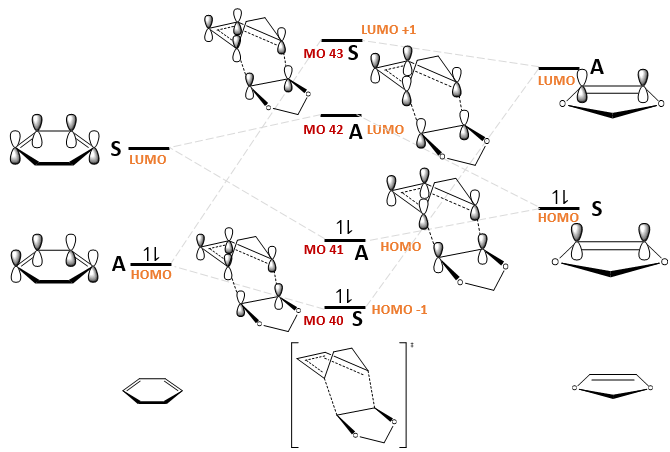
The MO diagrams for the formation of the endo and exo transition states, as well as the relevant MOs, are shown in Fig. 9 and Table 7 respectively. The relative ordering of the MO energies were based on the orbital energies obtained from a BY3LYP/6-31(d) optimisation of the reactants and transition states, but exact energies were not considered for simplicity.

Formation of Endo TS	Formation of exo TS
Fig. 9: MO diagrams for the formation of the (A) endo TS and (B) exo TS

**Table 7: Relevant MOs in the endo and exo transition states**
	Endo TS	Exo TS
LUMO+1 (MO 43)
LUMO (MO 42)
HOMO (MO 41)
HOMO -1 (MO 40)

Fig. 11 shows that secondary orbital interactions exist only for the endo TS. This has a stabilising effect as demonstrated in Fig. 12. Note that not all the orbitals are drawn; only those interacting are shown for simplicity.

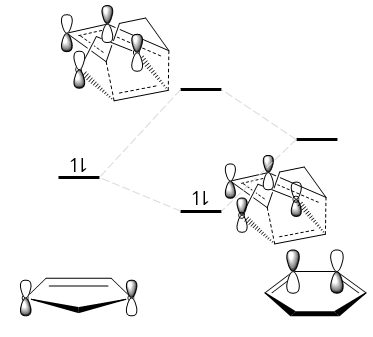
Fig. 12: Simplified MO diagram showing the secondary orbital interaction in the endo product

This secondary orbital interaction explains the endo rule, which states that the endo product is always preferentially formed in a Diels-Alder reaction.^[5]

Endo TS	Exo TS	Cheletropic
endo	exo	che

**Table 9: Energies of reactants, TS and products**
Xylylene		SO₂		Endo TS		Endo Product
Energy (Hartrees)	Energy (kJ mol^-1)	Energy (Hartrees)	Energy (kJ mol^-1)	Energy (Hartrees)	Energy (kJ mol^-1)	Energy (Hartrees)	Energy (kJ mol^-1)
0.178746	469.297659	-0.118614	-311.4210807	0.090562	237.770549	0.021701	56.9759798
Exo TS		Exo Product		Cheletropic TS		Cheletropic Product
Energy (Hartrees)	Energy (kJ mol^-1)	Energy (Hartrees)	Energy (kJ mol^-1)	Energy (Hartrees)	Energy (kJ mol^-1)	Energy (Hartrees)	Energy (kJ mol^-1)
0.092078	241.750807	0.021453	56.3248558	0.099062	260.087301	0.000005	0.013127501

**Table 10: Reaction barriers and energies for the reaction between xylylene and SO₂**
Reaction	Formation of Endo Product	Formation of Exo Product	Formation of Cheletropic Product
Reaction barrier/ kJ mol^-1	+79.9	+83.9	+102.2
Reaction energy/ kJ mol^-1	-100.9	-101.6	-157.9

↑ J. F. Chiang and S. H. Bauer, Journal of the American Chemical Society, 1969, 91, 1898–1901
↑ E. V. Anslyn and D. A. Dougherty, Modern physical organic chemistry, Univ. Science Books, Sausalito, CA, 2008, pp.22
↑ G. S. Manku, Theoretical principles of inorganic chemistry, Inter-India Publ., New Delhi, 1986, pp.97
↑ P. Atkins and J. De Paula, Atkins' Physical Chemistry, University Press, Oxford, 10th edn., 2014.
↑ J. García, J. Mayoral and L. Salvatella, European Journal of Organic Chemistry, 2004, 2005, 85-90.

[1] J. F. Chiang and S. H. Bauer, Journal of the American Chemical Society, 1969, 91, 1898–1901

[2] E. V. Anslyn and D. A. Dougherty, Modern physical organic chemistry, Univ. Science Books, Sausalito, CA, 2008, pp.22

[3] G. S. Manku, Theoretical principles of inorganic chemistry, Inter-India Publ., New Delhi, 1986, pp.97

[4] P. Atkins and J. De Paula, Atkins' Physical Chemistry, University Press, Oxford, 10th edn., 2014.

[5] J. García, J. Mayoral and L. Salvatella, European Journal of Organic Chemistry, 2004, 2005, 85-90.

[1]

[2]

[3]

[4]

[5]