Rep:Mod:ts cyy113

Introduction

In your introduction, briefly describe what is meant by a minimum and transition state in the context of a potential energy surface. What is the gradient and the curvature at each of these points? (for thought later on, how would a frequency calculation confirm a structure is at either of these points?)

The dynamics of a chemical reaction can be investigated using a potential energy surface (PES) obtained by plotting $V(q_1,q_2)$ against $q_1$ and $q_2$, where $V(q_1,q_2)$ is the potential energy and $q_1$, $q_2$ are order parameters of a reaction. Reactants and products occur at the minimum of the PES while transition states occur at the saddle point. Mathematically, they are both stationary points, so the gradient (i.e. the first derivative $\frac{\partial V}{\partial q_i}$) of both the minimum and the saddle point is 0. However, the curvature of the minimum is concave while that of the saddle point is convex. Thus, they can only be distinguished by taking the second derivative $\frac{{\partial }^{2}V}{\partial q_i^2}$, which will be positive for the minimum, but negative for the saddle point.

Nf710 (talk) 09:59, 16 November 2017 (UTC) Careful here. Your have defined your PES with only 2 dimensions. It is 3N-6 dimensions. secondly at a saddle point you need at least 2 dimensions so it is the curvature of only 1 that is convex at a first order saddle point.

Since a chemical bond can be modelled as a spring, Hooke's Law (eq. 1) can be invoked, where $V$ is the elastic potential energy, $k$ is a constant and $x$ is the displacement of the particle from its equilibrium position.

$V=\frac{1}{2}k{x}^2$ Equation 1: Hooke's Law

Taking the second derivative of this equation results in eq. 2. Thus, $k$ will be positive for all minimum points but negative for saddle points. Physically, this means that all coordinates have been minimised for reactants and products, but some coordinates have not been minimised for transition states. Thus, reactants and products remain stable unless they are excited with energy but transition states are inherently unstable and will rearrange into a stable form spontaneously.

Nf710 (talk) 11:11, 16 November 2017 (UTC) Again how many dimensions are you talking about

$\frac{{\partial }^{2}V}{\partial x^2}=k$ Equation 2: Second derivative of Hooke's Law

Since the vibrational frequency $\omega$ is a function of $\sqrt{k}$ (eq. 3), reactants and products will always give real frequencies, while transition states will give imaginary frequencies. A well-chosen reaction coordinate will only result in a transition state with one imaginary frequency, as all other coordinates have been minimised.

$\omega =\frac{1}{2\pi }\sqrt{\frac{k}{m}}$ Equation 3: Relation between frequency and $k$

In these exercises, computational methods were used to determine suitable reaction coordinates of several [4+2] Diels-Alder cycloadditions. The coordinates of the reactants, transition state (TS) and products were optimised using Gaussian, from which an Intrinsic Reaction Coordinate (IRC) calculation was run to visualise the approach trajectory of the reactants to form a transition state and subsequently the product. Further observable parameters (Bond Length and Energies) were also analysed from the optimised coordinates and IRC calculation. The wavefunctions of the optimised species were visualised as molecular orbitals (MOs) and their shapes and symmetries were compared to theoretical predictions.

Optimisation was conducted at the semi-empirical PM6 level first, before some calculations were refined using Density Functional Theory (DFT) methods at the BY3LP/6-31(d) level. The PM6 optimisation uses a fitted method drawing on experimental data, hence it is less accurate. However, it saves computational resources and is a good starting point for initial calculations. The BY3LYP/6-31(d) optimisation is more accurate but it comes at the cost of computational effort.

Exercise 1

(Fv611 (talk) Very well done. A well structured answer and very good critical discussions across the whole exercise.)

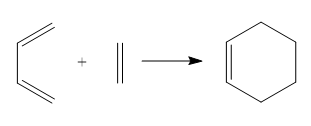
The following Diels-Alder cycloaddition was investigated. Butadiene was the diene while ethene was the dienophile. Butadiene had to be in the correct s-cis conformation so that there is effective spatial overlap with ethene. Reactants, TS and products were optimised at the PM6 level.

Fig 1: Scheme of reaction between butadiene and ethene. Scheme was generated via ChemDraw

Optimisation Results

1) Optimise the reactants and TS at the PM6 level.

Butadiene (s-cis)	Ethene	TS

Fig. 2: Optimised JMol files reactants and TS

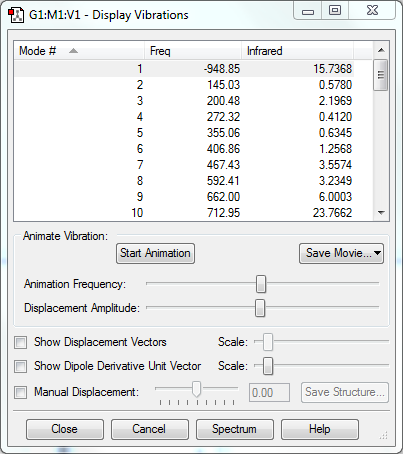
2) Confirm that you have the correct TS with a frequency calculation and IRC.
Frequency Calculation

Fig. 3: Frequency values of butadiene/ethene TS

To confirm that the TS is correctly optimised, its frequencies must be calculated and checked that there is only 1 imaginary vibration. This is represented by GaussView as a negative vibration. Since the TS occurs on a maximum point on the Free Energy surface, the second derivative of such a point is negative. Frequency values are in fact the second derivatives of energy, hence a single negative frequency suggests that there is only 1 TS on the reaction coordinate chosen. This would be indicative of a good reaction coordinate, as additional negative frequencies suggests the presence of more than 1 stationary point, which could be a maximum in the order parameter chosen but a minimum in another order parameter. The transition state has been computed correctly as it only shows 1 negative frequency. (Fig. 3)

IRC
A well-defined, asymmetric Free Energy Surface was obtained, further confirming that the reaction coordinate was well chosen. (Fig. 4) A predicted trajectory was computed using a Intrinsic Reaction Coordinate function on Gaussian. (Fig. 5)

Fig. 4: Free Energy Profile of reaction

Fig. 5: Trajectory of Butadiene/Ethene molecules

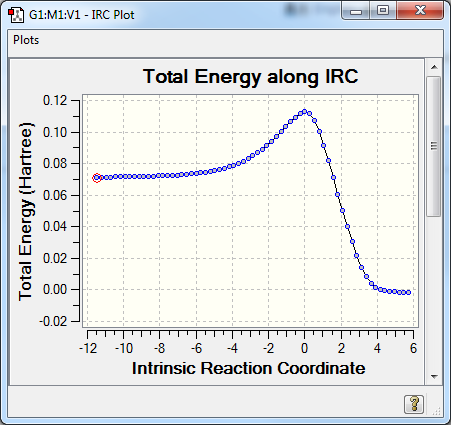3) Optimise the products at the PM6 level.

Cyclohexene

Fig. 6 Optimised JMol file of cyclohexene

Analysis of MO diagrams

Construct an MO diagram for the formation of the butadiene/ethene TS, including basic symmetry labels (symmetric/antisymmetric or s/a).
Based on the values obtained from a Gaussian calculation using the PM6 basis set, secondary orbital mixing between the MOs of the transition state is expected, which stabilises LUMO+1 and destabilises the HOMO, as illustrated with the red arrows and energy levels.

Fig 7: MO diagram showing the formation of the butadiene/ethene TS

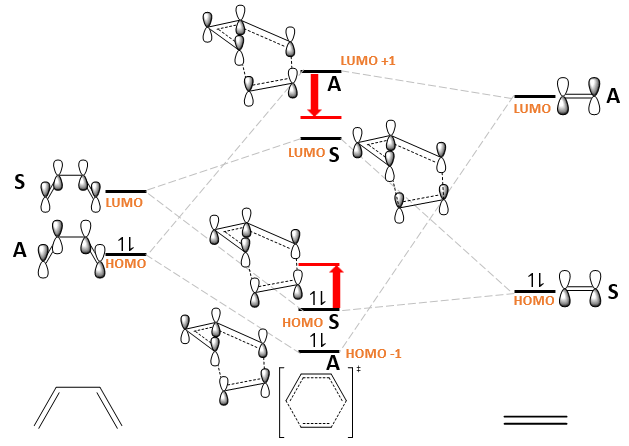
The HOMO-LUMO energy gap in butadiene is smaller than ethene due to increased conjugation. In fact, this reaction is reported to proceed inefficiently. The reaction will proceed more efficiently if butadiene is made more electron rich by adding electron donating groups, or ethene is made more electron poor by adding electron withdrawing groups. Adding electron donating groups raises the energy levels, while adding electron withdrawing groups lower the energy levels. This effectively reduces the HOMO-LUMO energy gap allowing for more efficiency overlap.

(Fv611 (talk) Good discussion about the reaction efficiency.)
For each of the reactants and the TS, open the .chk (checkpoint) file. Under the Edit menu, choose MOs and visualise the MOs. Include images (or Jmol objects) for each of the HOMO and LUMO of butadiene and ethene, and the four MOs these produce for the TS. Correlate these MOs with the ones in your MO diagram to show which orbitals interact.

Table 1: Selected JMol images showing MOs of Butadiene, Ethene and Butadiene/Ethene TS

Butadiene Ethene HOMO LUMO

Butadiene/Ethene TS LUMO+1 LUMO HOMO HOMO-1

(Fv611 (talk) Would have been helpful to add symmetry labels to the MO table, or to number them both in the table and in the MO diagram.)

What can you conclude about the requirements for symmetry for a reaction (when is a reaction 'allowed' and when is it 'forbidden')?

The MOs of the transition state are all formed by overlapping and mixing reactant MOs of the same symmetry (Fig. 5), suggesting that a reaction is only allowed when reactant MOs of the same symmetry overlap. This can be justified mathematically. As the coordinates of the atoms change along a reaction coordinate, the wavefunctions of the reactant MOs (denoted as ${\psi }_a$ and ${\psi }_b$) can no longer describe the electron density of the transition state. A transition state wavefunction (denoted as $\psi$) will better describe this electron density (as ${\psi }^2$). The energy of the transition state wavefunction $E_{\psi }$ is given via the Hamiltonian $\hat{H}$ as follows:

$E_{\psi }=\frac{<{\psi }_a|\hat{H}|{\psi }_a>\pm 2<{\psi }_a|\hat{H}|{\psi }_b>+<{\psi }_b|\hat{H}|{\psi }_b>}{2(1\pm <{\psi }_a|{\psi }_b>)}$ Equation 4: Energy of transition state wavefunction

The Hamiltonian is a totally symmetric operator, meaning that $\hat{H}|\psi >$ has the same symmetry as $\psi$. If the symmetries of ${\psi }_a$ and ${\psi }_b$ were different, $E_{\psi }$ would be the sum of $E_{{\psi }_a}$ and $E_{{\psi }_b}$, which cannot be the case since the reactants are not at infinite separation.

Write whether the orbital overlap integral is zero or non-zero for the case of a symmetric-antisymmetric interaction, a symmetric-symmetric interaction and an antisymmetric-antisymmetric interaction.

The orbital overlap integral $S$ quantifies the extent of overlap between reactant MOs (denoted by ${\psi }_1$ and ${\psi }_2^{*}$). It is given by the following equation.

$S=\int {\psi }_1{\psi }_2^{*}d\tau$ Equation 5: Equation of the overlap integral

The possible values of $S$ depends on ${\psi }_1$ and ${\psi }_2^{*}$ and they are as follows:

Table 2: Summary of the possible values of $S$

Type of interaction	Symmetric-Antisymmetric	Symmetric-Symmetric	Antisymmetric-Antisymmetric
Value of $S$	Zero	Non-Zero	Non-Zero

(Fv611 (talk) Very good symmetry discussion, although you could have pointed out that the orbital overlap is directly related to the symmetry requirements, as the reaction cannot happen with overlap zero.)

Bond Length Analysis

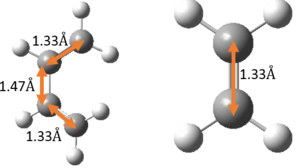
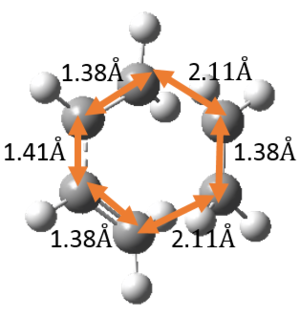
Include measurements of the 4 C-C bond lengths of the reactants and the 6 C-C bond lengths of the TS and products. How do the bond lengths change as the reaction progresses? What are typical sp³ and sp² C-C bond lengths? What is the Van der Waals radius of the C atom? How does this compare with the length of the partly formed C-C bonds in the TS.

The relevant C-C bond lengths are tabulated below:

Table 3: Summary of C-C bond lengths and Van Der Waals radius

Reactant C-C bond lengths	TS C-C bond lengths	Product C-C bond lengths
Reported sp2 and sp3 bond lengths in cyclohexene /Å	Typical sp2 and sp3 bond lengths /Å	Van Der Waals' radius of C atom /Å
	sp2-sp2 C-C = 1.31-1.34 sp2-sp3 C-C = 1.50 sp3-sp3 C-C = 1.53-1.55	1.70

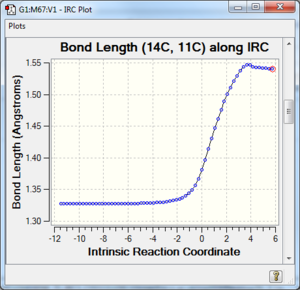
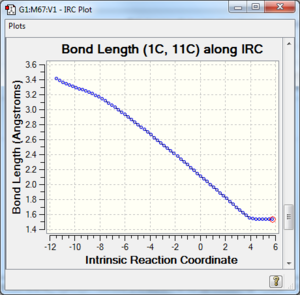
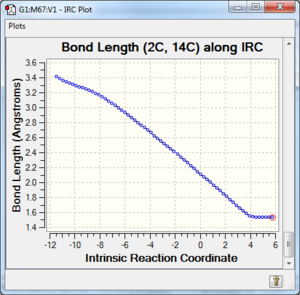
The partly formed C-C bond lengths are between a (C-C) single bond length and twice the Van Der Waals radius of C. This shows that a bond is indeed being formed. In addition, the C-C bond lengths in the cyclohexene product agreed well with literature values of cyclohexene and average sp² C sp² C, sp² C sp³ C and sp³ C sp³ C bond lengths as well. This is further support that the cyclohexene product and TS has been optimised well.

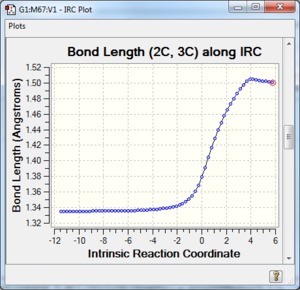
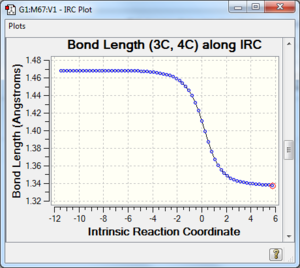
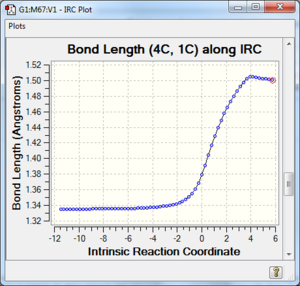
Along the reaction coordinate, graphs showing the change in various C-C bond lengths are shown in the table below. The atoms are labelled based on Fig. 8.

Fig 8: Labelled atoms of reactants

Table 4: Change in bond lengths with reaction coordinate

Bond length between	C2 and C3	C3 and C4	C4 and C1
Graph showing the change in Bond Length with Reaction Coordinate	Bond length increases	Bond length decreases	Bond length increases
Bond length between	C11 and C14	C1 and C11	C2 and C14
Graph showing the change in Bond Length with Reaction Coordinate	Bond length increases	Bond length decreases	Bond length decreases

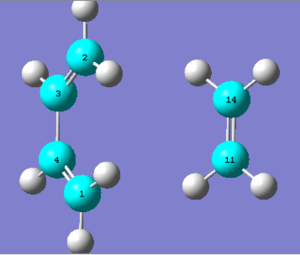
Vibrational Analysis

Illustrate the vibration that corresponds to the reaction path at the transition state. Is the formation of the two bonds synchronous or asynchronous?
The vibration that corresponds to the reaction path occurs at $-949c{m}^{-1}$. The formation is synchronous as expected of a typical Diels Alder cycloaddition.

Fig. 9: Reaction path vibration for Butadiene/Ethene TS

(Fv611 (talk) Very thorough analysis. The reference to literature values for cyclohexene was a very good addition.)

Exercise 2

In this exercise, the following reaction was investigated. Cyclohexadiene was the diene while 1,3-dioxole was the dienophile. Reactants, TS and products were optimised at both the PM6 and BY3LYP/6-31(d) levels.

Fig. 10: Scheme of reaction between cyclohexadiene and 1,3-dioxole generated by ChemDraw

Optimisation Results

Using any of the methods in the tutorial, locate both the endo and exo TSs at the B3LYP/6-31G(d) level (Note that it is always fastest to optimise with PM6 first and then reoptimise with B3LYP).
Method 3 was used and the following optimisations were obtained:

Table 5: JMol log files of reactants and TS at PM6 and BY3LP 6-31(d) level

	Endo TS	Exo TS	Cyclohexadiene	1,3-dioxole
PM6
B3LYP/6-31G(d)

Frequency Analysis

Confirm that you have a TS for each case using a frequency calculation.
The frequencies of each TS are shown in the table below. In each case, there is only 1 negative frequency which confirms that a TS has been located on a suitable reaction coordinate.

Table 6: Summary of frequency values

	Endo TS		Exo TS
Basis Set	PM6	BY3LYP/6-31G(d)	PM6	BY3LYP/6-31G(d)
Frequencies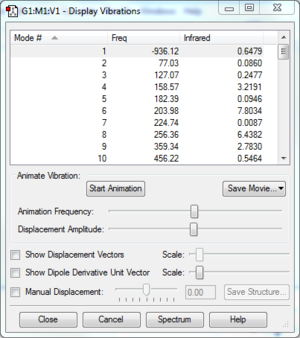

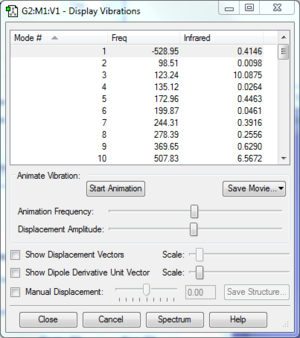MO Analysis

Using your MO diagram for the Diels-Alder reaction, locate the occupied and unoccupied orbitals associated with the DA reaction for both TSs by symmetry. Find the relevant MOs and add them to your wiki (at an appropriate angle to show symmetry). Construct a new MO diagram using these new orbitals, adjusting energy levels as necessary.
The MO diagrams for the formation of the endo and exo transition states, as well as the relevant MOs, are shown in Fig. 11 and Table 7 respectively. The relative ordering of the MO energies were based on the orbital energies obtained from a BY3LYP/6-31(d) optimisation of the reactants and transition states, but exact energies were not considered for simplicity.

Formation of Endo TS	Formation of Exo TS
Fig. 11: MO diagrams for the formation of the (A) endo TS and (B) exo TS

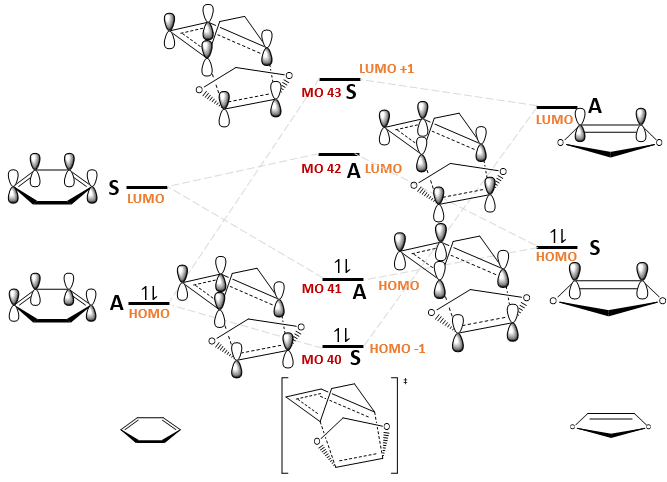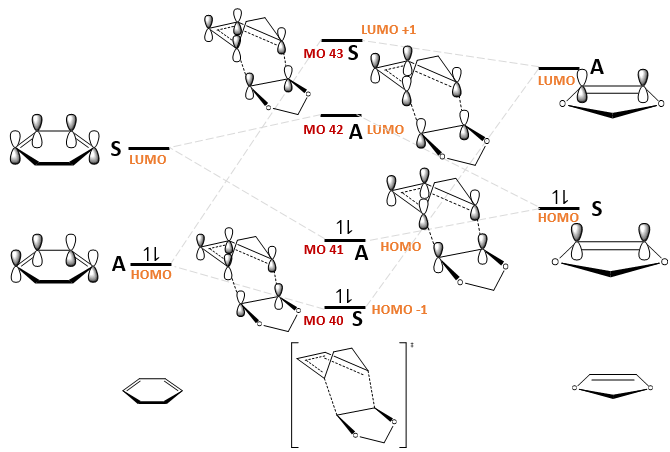(Why are the symmetry labels switching for your TS MOs? Tam10 (talk) 13:34, 10 November 2017 (UTC))

Table 7: Relevant MOs in the endo and exo transition states

	Endo TS	Exo TS
LUMO+1 (MO 43)
LUMO (MO 42)
HOMO (MO 41)
HOMO -1 (MO 40)

Is this a normal or inverse demand DA reaction?
This is an inverse demand DA reaction. In a normal demand DA reaction, the HOMO of the diene reacts with the LUMO of the dienophile but in an inverse demand DA reaction, the HOMO of the dienophile reacts with the LUMO of the diene. Thus, in this reaction, the HOMO of the dienophile 1,3-dioxole reacted with the LUMO of the diene, hexadiene. This can be rationalised by Molecular Orbital (FMO) theory, which states that the rate of a Diels-Alder reaction is faster if the energy gap between the overlapping HOMO and LUMO orbitals is smaller. Based on the energy calculations of cyclohexadiene and 1,3-dioxole at the BY3LYP/6-31(d) level, it is found that the energy gap between LUMO (hexadiene) and HOMO (1,3-dioxole) is smaller than that between HOMO (hexadiene) and LUMO (1,3-dioxole).

In addition, the symmetries of the LUMO +1, LUMO, HOMO and HOMO +1 molecular orbitals in the transition state are all reversed in an inverse demand Diels-Alder reaction. This is reflected in the A-S-S-A ordering of these transition state MOs, which should have been S-A-A-S in a normal demand Diels-Alder reaction.

In fact, it is expected that this Diels Alder cycloaddition proceeds with inverse demand. Electrons can be donated into the dienophilic double bond via resonance effect from the adjacent oxygen atoms. Thus, the energies of the dienophile MOs will increase in energy such that the HOMO of the dienophile will be closer in energy to the LUMO of the diene.

Reaction Barriers and Reaction Energies

In the .log files for each calculation, find a section named "Thermochemistry". Tabulate the energies and determine the reaction barriers and reaction energies (in kJ/mol) at room temperature (the corrected energies are labelled "Sum of electronic and thermal Free Energies", corresponding to the Gibbs free energy).

The energies of reactants, TS and products are summarised in the table below.

Table 8: Summary of the energies of reactants, TS and products

		Cyclohexadiene		1,3-dioxole		Endo TS
		Energy (Hartrees)	Energy (kJ mol-1)	Energy (Hartrees)	Energy (kJ mol-1)	Energy (Hartrees)	Energy (kJ mol-1)
Basis Set	PM6	0.116877	306.860587	0.052276	137.250648	0.137939	362.158872
	BY3LYP/6-31(d)	-233.324375	-612593.19323	-267.068650	-701188.79399	-500.332148	-1313622.1546
		Exo TS		Endo Product		Exo Product
		Energy (Hartrees)	Energy (kJ mol-1)	Energy (Hartrees)	Energy (kJ mol-1)	Energy (Hartrees)	Energy (kJ mol-1)
Basis Set	PM6	0.138903	364.689854	0.037804	99.2544096	0.037977	99.7086211
	BY3LYP/6-31(d)	-500.329168	-1313614.3306	-500.418691	-1313849.3733	-500.417320	-1313845.77374

The reaction barriers (i.e. activation energy) and reaction energies (i.e. $\mathrm{\Delta }G$) were then calculated using energy values obtained from the BY3LYP/6-31G(d) basis set, as they are more accurate. The reaction barrier is the difference between the energies of the TS and the reactants, while the reaction energy is the difference between the energies of the reactants and products. They are summarised in the table below:

Table 9: Reaction barrier and energy of the reaction between cyclohexadiene and 1,3-dioxole

Reaction	Formation of Endo Product	Formation of Exo Product
Reaction barrier/ kJ mol-1	+160	+168
Reaction energy/ kJ mol-1	-67.4	-63.8

Which are the kinetically and thermodynamically favourable products?
In this reaction, the endo product has a lower activation energy and hence the kinetically favourable product. This is in agreement with the fact that secondary orbital interactions exist only for the endo product in any Diels-Alder cycloaddition involving substituted dienophiles. In this example, it is illustrated in Fig. 13.

In addition, in this reaction the endo product has a more negative reaction energy and is hence the thermodynamically favourable product. This deviates from the fact that the endo product suffers from steric clash. However, since a significant extent of distortion is required from cyclohexadiene to form the transition state, it is likely that the reaction proceeds with a late transition state. By Hammond's Postulate, this means that the transition state resembles the products. As such, the same secondary orbital interactions that stabilise the endo transition state will also stabilise the endo product, leading to a more negative reaction energy.

Nf710 (talk) 11:37, 16 November 2017 (UTC) This is a good theory with Hammonds postulate. You can actually see this in the MOs of the product. Howevrr in this caze the sterics are only present in the exo

Look at the HOMO of the TSs. Are there any secondary orbital interactions or sterics that might affect the reaction barrier energy (Hint: in GaussView, set the isovalue to 0.01. In Jmol, change the mo cutoff to 0.01)?

HOMO of Endo TS	HOMO of Exo TS
Fig. 12: Analysis of secondary orbital overlaps in the HOMO of endo and exo TS

Fig. 12 shows that secondary orbital interactions exist only for the endo TS. This has a stabilising effect as demonstrated in Fig. 13. Note that not all the orbitals are drawn; only those interacting are shown for simplicity.

Fig. 13: Simplified MO diagram showing the secondary orbital interaction in the endo product

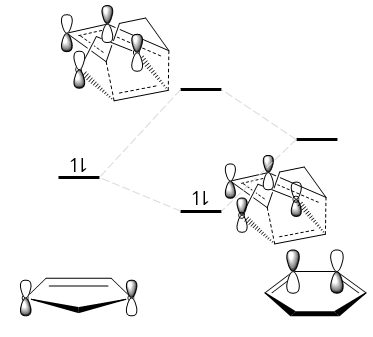
This secondary orbital interaction explains the endo rule, which states that the endo product is always preferentially formed in a Diels-Alder reaction.

Exercise 3

The Diels-Alder reaction between o-xylylene and SO₂ is investigated in this exercise. o-xylylene is the diene while SO₂ is the dienophile.

Fig. 14: Reaction scheme between o-xylylene and SO₂

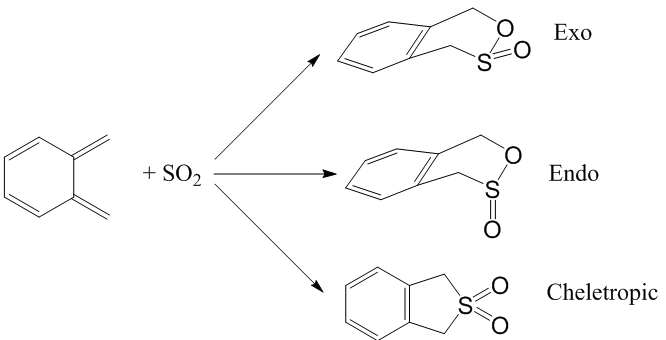
Optimisation Results

1) Optimise the TSs for the endo- and exo- Diels-Alder and the Cheletropic reactions at the PM6 level.
The endo and exo TS each have a pair of enantiomers. In each case, only 1 enantiomer is displayed in the JMol files in the figure below.

Exo TS	Endo TS	Cheletropic TS

Fig. 15: Optimised JMol files of the endo, exo and cheletropic TS

(Make sure you use the correct frame to display your Jmols. These are all showing the input file Tam10 (talk) 13:38, 10 November 2017 (UTC))

Reaction Barriers and Reaction Energies

3) Calculate the activation and reaction energies (converting to kJ/mol) for each step as in Exercise 2 to determine which route is preferred.
The energies of the reactants, TS and products for the endo, exo and cheletropic reactions are summarised below:

Table 10: Energies of reactants, TS and products

o-xylylene		SO2		Endo TS		Endo Product
Energy (Hartrees)	Energy (kJ mol-1)	Energy (Hartrees)	Energy (kJ mol-1)	Energy (Hartrees)	Energy (kJ mol-1)	Energy (Hartrees)	Energy (kJ mol-1)
0.178044	467.454558	-0.118614	-311.4210807	0.090562	237.770549	0.021701	56.9759798
Exo TS		Exo Product		Cheletropic TS		Cheletropic Product
Energy (Hartrees)	Energy (kJ mol-1)	Energy (Hartrees)	Energy (kJ mol-1)	Energy (Hartrees)	Energy (kJ mol-1)	Energy (Hartrees)	Energy (kJ mol-1)
0.092078	241.750807	0.021453	56.3248558	0.099062	260.087301	0.000005	0.013127501

Taking the same differences in energies as in Exercise 2, the reaction barrier (activation energy) and reaction energies are as follows:

Table 11: Reaction barriers and energies for the reaction between xylylene and SO₂

Reaction	Formation of Endo Product	Formation of Exo Product	Formation of Cheletropic Product
Reaction barrier/ kJ mol-1	+81.7	+85.7	+104.0
Reaction energy/ kJ mol-1	-99.1	-99.4	-155.7

4) Using Excel or Chemdraw, draw a reaction profile that contains relative heights of the energy levels of the reactants, TSs and products from the endo- and exo- Diels-Alder reactions and the cheletropic reaction. You can set the 0 energy level to the reactants at infinite separation.
The relative energy levels are shown in the figure below, generated on ChemDraw.

Fig. 16: Energy profile diagrams of the endo, exo and cheletropic reactions

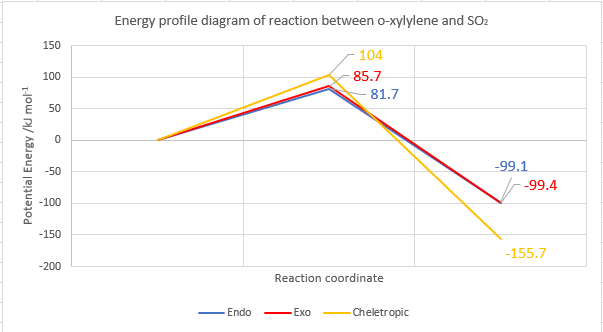
Between the endo/exo pathways, the endo product is kinetically favoured due to secondary orbital overlap. The exo product is thermodynamically favoured as it has less steric hindrance. These factors were previously discussed in Exercise 2 under section 3.4. Considering the cheletropic reaction and both Diels Alder reactions, the cheletropic TS has a higher energy than the Diels Alder TS, as it is more planar and there are strong eclipsing interactions developing between the aromatic 6-membered ring and the sulphone oxygen atoms which destabilises the TS. However, the cheletropic product is more stable than both Diels-Alder products. Although a 5-membered ring typically suffers from more torsional strain than 6-membered rings, in this case the presence of a large sulfur atom would cause more distortions in the 6-membered ring. Thus, it can be concluded that the cheletropic pathway is under thermodynamic control while the Diels-Alder pathway is under kinetic control. The cheletropic product will be formed in equillibrating conditions.

IRC Analysis

2) Visualise the reaction coordinate with an IRC calculation for each path. Include a .gif file in the wiki of these IRCs.
The following figures illustrate the approach trajectory between o-xylylene and SO₂ for the endo, exo and cheletropic reactions:

(A): Approach trajectory for the formation of the endo product (B): Approach trajectory for the formation of the exo product (C): Approach trajectory for the formation of the cheletropic product Fig. 17: IRC visualisations of the approach trajectory between o-xylylene and SO₂

Xylylene is highly unstable. Look at the IRCs for the reactions - what happens to the bonding of the 6-membered ring during the course of the reaction?
o-xylylene is unstable due to the presence of 2 dienes locked in an s-cis conformation, which can act as good dienes for Diels-Alder reactions. All the carbons are sp² hybridised, thus the molecule is planar. As SO₂ approaches o-xylylene from either the top or bottom face, the 6-membered ring becomes aromatic due to it having 6 $\pi$ electrons. It is further evidenced by measuring the C-C bond lengths, which lie between an sp²C-sp²C and sp³C-sp³C bond at 1.40 Angstroms. This has a stabilising effect.

Extension

There is a second cis-butadiene fragment in o-xylylene that can undergo a Diels-Alder reaction. If you have time, prove that the endo and exo Diels-Alder reactions are very thermodynamically and kinetically unfavourable at this site.
The reaction between SO₂ and the second cis-butadiene fragment is described in the scheme below. Similarly, endo and exo products are possible.

Fig. 18: Reaction scheme for an alternative reaction between o-xylylene and SO₂

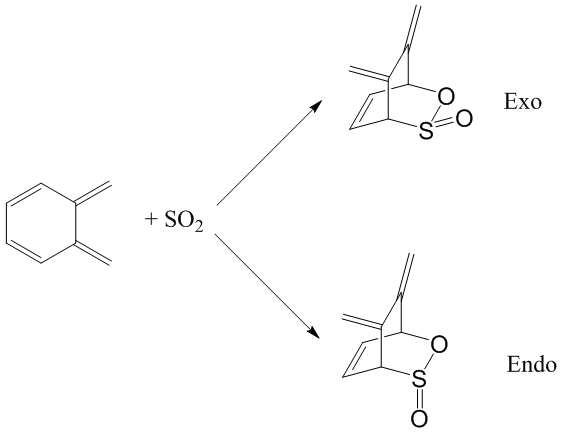
In a similar way as Exercise 3, the reactants, TS and products are optimised with Gaussian at PM6 energy level and the table below summarises their energies.

Table 12: Energies of the reactants, TS and products in the alternative reaction between o-xylylene and SO₂

Xylylene		SO2		Endo TS
Energy (Hartrees)	Energy (kJ mol-1)	Energy (Hartrees)	Energy (kJ mol-1)	Energy (Hartrees)	Energy (kJ mol-1)
0.178044	467.454558	-0.118614	-311.4210807	0.102070	267.98480541
Endo Product		Exo TS		Exo Product
Energy (Hartrees)	Energy (kJ mol-1)	Energy (Hartrees)	Energy (kJ mol-1)	Energy (Hartrees)	Energy (kJ mol-1)
0.065609	172.25644262	0.105054	275.81929801	0.067306	176.711916

Accordingly, the reaction barriers and reaction energies were calculated as follows:

Table 13: Reaction barrier and reaction energy for the alternative reaction between o-xylylene and SO₂

Reaction	Formation of Endo Product	Formation of Exo Product
Reaction barrier/ kJ mol-1	+107.9	+115.7
Reaction energy/ kJ mol-1	+12.2	+16.6

Both Diels-Alder pathways on this cis-butadiene fragment proceed with an activation energy barrier that is much larger than if it proceeded with the former cis-butadiene fragment in Exercise 3. Moreover, $\mathrm{\Delta }G$ is positive. This suggests that both reaction pathways at this cis-butadiene fragment are not feasible.

(Good extension Tam10 (talk) 13:39, 10 November 2017 (UTC))

Conclusion

The reaction dynamics of several Diels-Alder and a cheletropic reaction were analysed. From an optimisation of the atom coordinates in the reactants, transition state and products using Gaussian, various physical parameters (C-C bond lengths, free energies, MO energies) were extracted. In addition, an internal reaction coordinate (IRC) calculation was also run to visualise the trajectory of the reactants towards each other and how these physical parameters change along the reaction coordinate. The results obtained agreed with theory, in particular the Frontier Molecular Orbital theory, concerted mechanism of Diels-Alder reactions and the Endo Rule arising from secondary orbital interactions. The results also demonstrated that when SO₂ is used as a dienophile, the Diels-Alder pathway is kinetically controlled while the cheletropic pathway is thermodynamically controlled.

Log Files

Exercise 1

Species or IRC	Basis Set
	PM6
Butadiene	File:BUTADIENEWITHMO CYY113 2.LOG
Ethene	File:ETHENE WITHMO CYY113.LOG
Butadiene/Ethene TS	File:TS WITHMO CYY113.LOG
Cyclohexene	File:Cyclohexeneproduct cyy113.log
IRC	File:CYCLOHEXENE TS IRC3 CYY113.LOG

Exercise 2

Species or IRC	Basis Set
	PM6	BY3LYP/6-31(d)
Cyclohexadiene	File:CYCLOHEXADIENE MIN cyy113.LOG	File:CYCLOHEXADIENE MIN 631 CYY113.LOG
1,3-dioxole	File:DIOXOLE MIN cyy113.LOG	File:DIOXOLE631 2 cyy113.LOG
Endo TS	File:TS ex2 endo cyy113.LOG	File:Endots631mo cyy113.log
Exo TS	File:TS ex2 exo cyy113.LOG	File:Exots631mo2 cyy113.log
Endo Product	File:Endo PRODUCT MIN cyy113.LOG	File:ENDOPRODUCT 631 CYY113.LOG
Exo Product	File:ExoPRODUCT MIN cyy113.LOG	File:EXOPRODUCT631 CYY113.LOG

Exercise 3

Species or IRC	Basis Set
	PM6
o-xylylene	File:XYLENE3 cyy113.LOG
SO2	File:SO2 CYY113.LOG
Endo TS	File:EX3ENDOTS CYY113.LOG
Exo TS	File:XYLYLENE exoex3 TS cyy113.LOG
Cheletropic TS	File:INDENE TS cyy113.LOG
Endo Product	File:ENDOPRODUCT cyy113ex3.LOG
Exo Product	File:EXOPRODUCT OPT CYY113.LOG
Cheletropic Product	File:INDENEPRODUCT CYY113.LOG
Endo IRC	File:EX3ENDOTSIRC cyy113.LOG
Exo IRC	File:Xylene exo ts irccyy113.log
Cheletropic IRC	File:INDENEIRC CYY113.LOG

Extension

Species or IRC	Basis Set
	PM6
o-xylylene	File:Xylene cyy113.log
SO2	File:SO2 CYY113.LOG
Endo TS	File:Endotsextracyy113.log
Exo TS	File:Exotsextra cyy113.log
Endo Product	File:Endoproductmin4cyy113.log
Exo Product	File:EXOPRODUCTMIN4cyy113.LOG