Rep:Mod:ts Zh3615

^{This page was created by Zehua Hu, for third year computational laboratory Transition States and Reactivity.}

Introduction

Computational Chemistry is a commonly adopted method to optimize and calculate molecular structures and variations of their properties during a reaction because of its theoretical accuracy and cost-efficiency. Commonly the optimization are achieved by calculating the first and second derivative of the potential energy surface (PES). The PES is obtained by plotting the potential energy V(q1, q2, ..., qn) against order parameters q1, q2, ..., qn (where n=3N-6, N=number of atoms) for each reaction. The reactant(s) and product(s) of each reaction are the minimums of the PES respectively and the transition state(s) is the saddle point(s) of the PES between the reactant(s) and product(s). Knowing the whole PES is concave, the reactant(s) and product(s) hence have zero first derivative dV/dq_i and positive second derivative dV²/dq_i² while the transition state(s) has zero first derivative dV/dq_i and negative derivative dV²/dq_i².

Nf710 (talk) 22:05, 29 November 2017 (UTC) The TS only has this in 1 demensions there rest have positive curvature

In 1-dimension, with approximating the chemical bonds between atoms to harmonic oscillators, the vibration modes of chemical bonds then obey the Hooke's Law (eq.1), and the vibrational frequencies (ω) of harmonic oscillators obey the (eq.2):

Equation 1:

V = \frac{1}{2} k x^{2}

Equation 2:

ω = \frac{1}{2 π} \sqrt{\frac{k}{m}}

Where V is the elastic potential energy, k is the characteristic constant, x is the relative displacement of one atom to its connected atoms, m is the mass(for spring-mass model) or reduced mass (for atom-atom model). d²V/dx²=k can be obtained by differentiating the equation 1 twice, since the dV²/dq_i² is positive for reactant(s) and product(s) and negative for transition state(s) as suggested above, all vibrational frequencies are positive for reactant(s) and product(s) while a order parameter q that passes through the transition state produces one imaginary vibrational frequency. The only one imaginary vibrational frequency hence can be considered as the criteria for a successfully optimized transition state for multiple-transition-state reactions (e.g. exo- and endo-transition states).

In this computational laboratory, Gaussian worked similarly but in multiple dimensions to optimize and calculate reactant/product structures (min) and transition state structures (saddle point), relevant data was also obtained from the results of calculation and optimization e.g. bond lengths, MOs and energies. The less accurate semi-empirical method PM6 was applied for quick calculation and the DFT method BY3LYP/6-31(d) was used to obtain refined data e.g. for energy calculations.

Nf710 (talk) 22:11, 29 November 2017 (UTC) Good understanding of the vibrations

Butadiene and Ethylene

Procedure: The structures of butadiene and ethylene were drawn in Gaussview. Optimized structures, MOs and corresponding bond lengths of reactants were obtained from optimizing to PM6 level. The optimized structure of transition state was obtained by drawing guessed structures, optimizing to minimum (PM6), then optimizing to transition state (PM6, Berny, calculating force constancts for once) allowing Opt=NoEigen after freezing the bond lengths between two reaction sites of two alkenes to lengths of corresponding literature range, followed by IRC analysis (PM6). IRC analyzed structure i.e. the product cyclohexene was then optimized (PM6) to minimum to obtained optimized reaction product structure. Transition state was confirmed with frequency calculation (only 1 imaginary frequency) and IRC(correct shape).

Fig 1.1 Reaction scheme and bond lengths (unit: Å)

Fig 1.2 literature bond lengths(unit: Å)[1]

Log file download
Butadiene (minimum)	Ethylene (minimum)	Transition state (T.S. Berny)	IRC analysis	Cyclohexene (minimum)
File:Butadiene zh3615.LOG	File:Ethylene zh3615.LOG	File:1tstots zh3615.LOG	File:1tstoirc zh3615.LOG	File:1ptomin zh3615.LOG

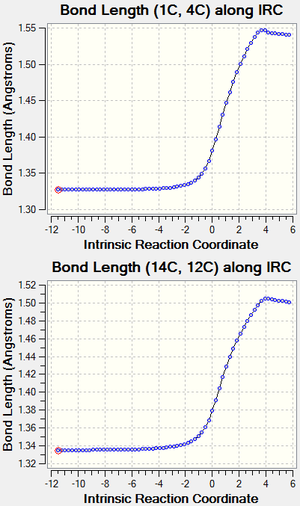
The carbon-carbon bonds lengths and their variation during the reaction are shown in the figure 1.1 and the literature bond lengths are shown in the figure 1.2, all obtained values are in literature range. The Van Der Waals radius of carbon atoms is 1.7 Å. [2] Detailed variation of bond lengths with time is shown in the table 1.1. As the reaction proceeds,the bond lengths of double bonds in both alkenes increases as they are gradually transformed to single carbon-carbon bonds, the bond length of the only single bond in the butadiene decreases as it was transformed to a double carbon-carbon bond gradually. The forming single carbon-carbon bonds of transition state between two alkenes have a bond length of 2.115 Å, which are shorter than two times of Van der Waals radius of carbon (3.4 Å).

(Fv611 (talk) You are not comparing the value of the bonds being formed at the TS with a typical sp3-sp3 bond length.)

Table 1.1 Bond lengths variations

MO diagram (fig 1.3) was constructed with symmetry labels in normal demand DA according to the relatively heights of MOs calculated. HOMOs-LUMO region orbitals were visualized in table 1.2 and 1.3. *NB height of each T.S. MO is the height of corresponding product. (Fv611 (talk) It is unclear what you mean by height, or corresponding product.)

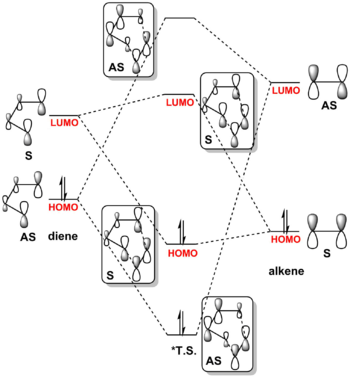
Fig 1.3 MO diagram of the Diels-Alder reaction

(Fv611 (talk) Your MO combinations are correct, but your energy levels are wrong. As the JMols are not included, as as you have not specified why they are not included, I cannot tell whether you have calculated the MOs correctly. In this reaction, both HOMOs of the reactants are lower in energy than the TS HOMO-1, and the ethene LUMO is higher in energy than the TS LUMO+1. Additionally, you have not labelled your MOs consistently between your table with the pictures and the MO diagram.)

The energy gap between HOMO and LUMO is smaller for butadiene due to its stronger conjugation system. The HOMO and LUMO of the transition state is formed by the interaction between the HOMO of ethylene and LUMO of butadiene. Both the reacting orbitals and formed orbitals are symmetric, which indicates that the reacting orbitals in the allowed Diels-Alder reaction for 6-pi-electron system should have the same symmetry. It can be mathematically demonstrated by observing the equation of wavefunction overlap integral (S) (eq. 4) below:

Equation 4:

S = \int ψ_{a} ψ_{b}^{*} d τ

Where ψ_a and ψ_b are the wavefunctions of reactant MOs, for these MOs to react, they must have non-zero wavefunction overlaps. S is non-zero for S-S, AS-AS interactions and is zero for S-AS and AS-S interactions. Hence Diels-Alder reaction is allowed for MOs of the same symmetry and forbidden for the MOs of different symmetries.

Table 1.2 MOs and corresponding visualizations of reactants
	LUMO	HOMO
Butadiene MO
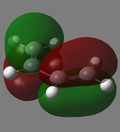
Butadiene MO Visualization
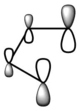
Ethylene MO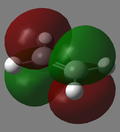
Ethylene MO Visualization

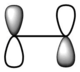Table 1.3 MOs and corresponding visualizations of transition states
	LUMO+1	LUMO	HOMO	HOMO-1
T.S. MO
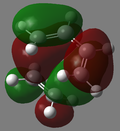
T.S. MO Visualization

As shown in the IRC analysis in table 1.4, the vibration that passes through the transition state is -949 cm^-1, the variation of the bond lengths of forming bond is identical in shape and value, which indicates that the new c-c single bonds are made simultaneously during the approaching of alkenes. In contrast, asynchronous formation of new bonds will produce different bond length curves between two forming bonds.

Table 1.4 IRC analysis
Transition state vibration	Transition state animation

Cyclohexadiene and 1,3-Dioxole

Procedure:The structures of cyclohexa-1,3-diene, 1,3-dioxole and their corresponding Diels-Alder products via exo- and endo- transition states were drawn in Gaussview. Optimized structure were obtained by optimizing to PM6 level. The optimized transition states were obtained by breaking the formed bond in the D-A reaction, then optimizing to transition state (PM6, Berny, calculating force constants for once) allowing Opt=NoEigen after freezing the bond lengths between two reaction sites of two alkenes to lengths of corresponding literature range, followed by IRC analysis (PM6), where MOs of transition states were also obtained. Orders of MOs via each reaction pathway were generated from the single point energy calculation. Each calculation was then further optimized to B3LYP/6-31G(d) level for the calculation of the reaction barriers and reaction energies at room temperature. Obtained transition states were confirmed with frequency calculation (only 1 imaginary frequency).

Fig 2.1 Reaction scheme

Log file download
Cyclohexadiene (minimum,PM6)	Cyclohexadiene (minimum,B3LYP)	1,3-dioxole (minimum,PM6)	1,3-dioxole (minimum,B3LYP)
File:Hextominpm6 zh3615.LOG	File:Hextomin631 zh3615.LOG	File:Diotominpm6 zh3615.LOG	File:Diotomin631 zh3615.LOG
Exo-T.S. (T.S. Berny,PM6)	Exo-T.S. (T.S. Berny,B3LYP)	Exo-T.S. IRC	Exo-T.S. energy analysis
File:2EXOtoTSpm6 zh3615.LOG	File:2EXOtoTS631 zh3615.LOG	File:2EXOtoIRC zh3615.LOG	File:2EXOtoENERGY zh3615.LOG
Endo-T.S. (T.S. Berny,PM6)	Endo-T.S. (T.S. Berny,B3LYP)	Endo-T.S. IRC	Endo-T.S. energy analysis
File:2ENDOtoTSpm6 zh3615.LOG	File:2ENDOtoTS631 zh3615.LOG	File:2ENDOtoIRC zh3615.LOG	File:2ENDOtoENERGY zh3615.LOG
Exo-reaction product (minimum,PM6)	Exo-reaction product (minimum,B3LYP)	Endo-reaction product (minimum,PM6)	Endo-reaction product (minimum,B3LYP)
File:Exoproductpm6 zh3615.LOG	File:EXOproduct631 zh3615.log	File:Endoproductpm6 zh3615.LOG	File:ENDOproduct631 zh3615.log

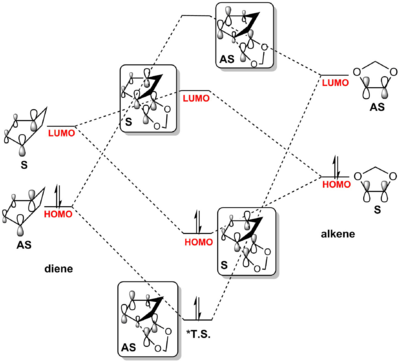
The MO diagram of this reaction was drawn according to the MO order calculated from energy analysis in the Gaussview as shown in table 2.1 following the rule in the figure 1.3. The energy gap between the LUMO of diene and the HOMO of alkene was calculated to be smaller than the energy gap between the HOMO of diene and LUMO of alkene. It suggested that both reactions are reverse demand Diels-Alder reactions. In a normal demand D-A reaction the HOMO of diene reacts with the LUMO of the alkene while the HOMO of the alkene reacts with the LUMO of diene in an inverse demand D-A reaction. In both reactions, the HOMO of alkene react with the LUMO of diene,

(Fv611 (talk) The HOMO of the diene reacting with the LUMO of the dienophile does not prevent the LUMO of the diene from reacting with the HOMO of the dienophile. In fact, in both this exercise's and the previous exercise's reactions both of this pairing. However this reaction is inverse electron demand whereas the reaction between butadiene and ethene is normal demand. The difference is given by whether the diene's or the dienophile's HOMO has the lowest energy, and on which LUMO has the highest energy. Your reactant's FMO's have the correct energies, but your TS MO's relative energies are not correct. Additionally, you correctly say that the symmetry of the TS MOs is A-S-S-A (for HOMO-1, HOMO, LUMO and LUMO+1 respectively) but you show in table 2.3 a symmetric LUMO+1 and an antisymmetric LUMO for the exo case. It would also have been nice to include a comment on the difference between the exo and endo case.)

The HOMO-LUMO region orbitals of the endo- and exo- transition states were visualized and shown in two different angle (for view of overlap and symmetry respectively) in the table 2.2. The activation energies, reaction energies and other related data were calculated and tabulated in table 2.3.

Table 2.1 MO diagrams via two T.S.
MO diagram via exo-T.S.	MO diagram via endo-T.S.

Table 2.2 Visualization of Molecular orbitals
	Exo- transition state (side view)	Exo- transition state (top view)	Endo- transition state (side view)	Endo- transition state (top view)
LUMO+1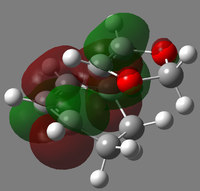
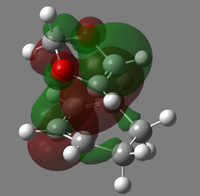
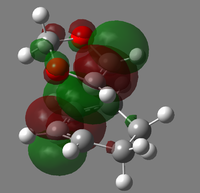LUMO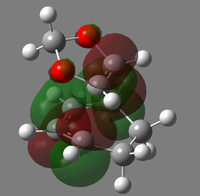
HOMO
HOMO-1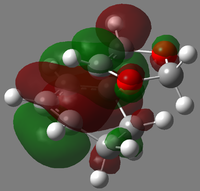

Table 2.3 Energy calculations of each reaction pathway (KJ/mol)
	via endo-Diels-Alder T.S.	via exo-Diels-Alder T.S.
Cyclohexadiene	306.9 (-612593)
1,3-dioxole	-137.3 (-701187)
Reactant sum	169.6 (-1313781)
Transition state	362.2 (-1313622)	364.7 (-1313614)
Reaction product	99.2 (-1313849)	99.7 (-1313846)
Activation energy	192.6 (159.0)	195.1 (167.0)
Reaction energy	-70.3 (-68.0)	-69.9 (-64.0)

NB the values in brackets were the value calculated from DFT-B3LYP-6-31G(d) method, the other values were the value calculated from PM6 method.

As shown in the table 2.3, both the activation energy and reaction energy via endo-transition state is less compared to the Diels-Alder reaction via exo-transition state, which indicates the endo-reaction product is both the kinetic and thermodynamic product. It is because of the favourable secondary orbital interactions during the formation of endo-product (lower the activation energy) and steric clashes in the exo-product (make the exo-product less thermodynamically stable), both effects are observable by comparing the HOMOs of transition states.

Nf710 (talk) 22:15, 29 November 2017 (UTC) This is a nice and consise section. However I think you could have gone into a bit more detail. Also it would have been nice if you had shown some more understanding of the quantum chemical methods going on. Also you energies seem to be slightly out.

O-Xylene-So₂ Cycloaddition

Procedure:The structure of 5,6-dimethylenecyclohexa-1,3-diene, sulphur dioxide and their corresponding products via exo-Diels-Alder, endo-Diels-Alder and cheletropic transition states were drawn in Gaussview. The optimized structures were obtained by optimizing to PM6. The optimized transition states were obtained by breaking the formed bond in each reaction, then optimized to transition state (PM6, Berny, calculating force constants for once), allowing Opt=NoEigen after freezing the bond lengths to lengths of corresponding literature range between two reaction sites of two alkenes followed by IRC analysis (PM6).

Fig 3.1 Reaction scheme

Log file download
O-Xylene(minimum,PM6)	SO₂(minimum,PM6)
File:Oxypm6zh3615.LOG	File:So2pm6zh3615.LOG
Exo-D-A-T.S.(T.S. Berny,PM6)	Exo-D-A-T.S.(IRC analysis)	Exo-D-A-product(minimum,PM6)
File:Daexototstspm6.log	File:Daexoirc zh3615.log	File:Daexoproductminpm6.LOG
Endo-D-A-T.S.(T.S. Berny,PM6)	Endo-D-A-T.S.(IRC analysis)	Endo-D-A-product(minimum,PM6)
File:Daendototstspm6.log	File:Daendoirc zh3615.log	File:Daendoproductminpm6.log
Cheletropic-T.S.(T.S. Berny,PM6)	Cheletropic-T.S.(IRC analysis)	Cheletropic-product(minimum,PM6)
File:Chetotstspm6.log	File:CHE IRC zh3615.log	File:Cheproductpm6 zh3615.LOG

Each reaction was visualized by carrying out IRC analysis at the PM6 level as shown in the table 1.6. Activation energies and reaction energies were calculated as shown in the table 1.7, and energy profiles are shown in figure 3.2.

Table 3.1 Animation from IRC analysis for each reaction pathway
	Endo-Diels-Alder T.S.	Exo-Diels-Alder T.S.	Cheletropic T.S.
Animation
Animation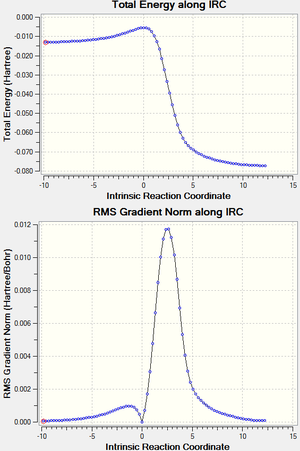

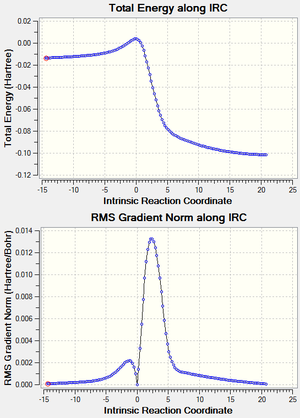
All carbons in o-xylylene is ^sp2 hybridised, which makes o-xylylene a planar molecule that can be attacked at the cis diene easily from both sides. During the approaching of SO2 molecule, the 6-membered ring quickly becomes 6 pi aromatic system by resonance with the two double bonds adjacent to the 6-membered ring. The structure of o-xylylene is changed due to the stabilization from aromatic system.

Table 3.2 Energy calculations of each reaction pathway (KJ/mol)
	via endo-Diels-Alder T.S.	via exo-Diels-Alder T.S.	via cheletropic T.S.
O-xylylene	467.2
Sulphur dioxide	-311.4
Reactant sum	155.8
Transition state	237.8	241.8	260.1
Reaction product	57.0	72.1	-0.00525
Activation energy	82.0	86.0	104.3
Reaction energy	-98.8	-83.7	-155.8

Among three reaction pathway, the most kinetically stable product is endo-Diels-Alder product (due to secondary orbital interactions) and the most thermodynamically stable product is cheletropic product (less steric hindrance between the 6-membered ring and sulphone oxygen compared to both Diels-Alder products), the ring strain is also not significant due to the size of sulphur atom.

(Just for the sake of communication, it's useful to have the energy differences on reaction profile diagrams Tam10 (talk) 11:32, 24 November 2017 (UTC))

Extension

The Diels-Alder reaction between o-xylylene and SO2 is possible but unfavourable in theory. The protocol in the section 3 was followed to calculate the reaction barriers and reaction energies of the below reaction as shown in the table 4.1.

Fig. 4.1 Reaction scheme

Table 4.1 Energy calculations of each reaction pathway (KJ/mol)
	via endo-Diels-Alder T.S.	via exo-Diels-Alder T.S.
O-xylylene	467.2
Sulphur dioxide	-311.4
Reactant sum	155.8
Transition state	268.0	275.8
Reaction product	172.3	176.7
Activation energy	95.7	99.1
Reaction energy	16.5	20.9

The reaction barrier and reaction energy is both positive and relatively large compared to the reaction at the other diene fragment in section 4, which indicates that this reaction are not spontaneous and are not likely to occur under normal conditions.

Log file download
Exo-D-A-T.S.(T.S. Berny,PM6)	Exo-D-A-product(minimum,PM6)
File:EXOTSTOTS444zh3615.LOG	File:EXOPRODUCTMIN444zh3615.LOG
Endo-D-A-T.S.(T.S. Berny,PM6)	Endo-D-A-product(minimum,PM6)
File:ENDOTSTOTS444ZH3615.LOG	File:ENDOPRODUCTMIN444zh3615.LOG

Conclusion

The structures of reactants, product and transition states of three Diels-Alder reactions were determined using GaussView 5.0.9. Semi-empirical method PM6, density functional theory method (DFT) B3LYP, IRC analysis and energy analysis were adopted in the optimization, visualisation and calculation. Theoretical values of bond lengths, MO order, sum of electronic and thermal free energies etc. were obtained and the competition between Dies-Alder reaction and Cheletropic reactions was investigated. All obtained data agreed with theory or was in literature range.

Reference

[1] E. V. Anslyn and D. A. Dougherty, Modern physical organic chemistry, Univ. Science Books, Sausalito, CA, 2008, pp.20-22

[2] A. Bondi, The Journal of Physical Chemistry, 1964, 68, 441-451.