Module 3

Cope rearrangement and Diels Alder cycloaddition reactions

We will be modelling the transition state of particular reaction to gain greater understanding of the reaction. This will be done by doing calculations to find and characterise transition structures on potential energy surface. We will start by modelling the reactants and products in the form of different conformations of the starting product of a cope rearrangement. In this case we will look at the reaction of 1,5-hexadiene, we will model a gauche and an app conformation to begin with, these are gauche and app relative to the middle carbons, this does mean that there are several app and gauche formations but we will not be looking at all just a particular conformations.

Our first calculations will be of the 1,5-hexadine with an anti linkage, this molecule will be made in gaussview. To run the calculations we will first make the molecules in gaussview then input the calculations into gaussian, we will be using the settings: Hartree Fock, 3-21G and memory set to 250MB. For the log file click here, for the .chk file click here. We can find the symmetry by chekcing the .chk file, in this case we find the molecule to have the symmetry Ci.

The next calculation will be of 1,5 hexadine with a gauche linkage, as with before this molecule will be made in gaussview. We will use the exact same calculation method as before (HF/5-21G).For the log file click here, for the .chk file click here. Again we can check the symmetry this time it is C2. I would expect the anti structure to be lower in energy due to sterics. However for these two conformers the gauche is slightly larger this is most likely due to the van der wals forces between the hydrogens in the gauche while these are not able in the anti conformation.

Final energy of structure anti/gauche
Anti	Gauche
-231.69253528	-231.69166702

Conformer	Structure	Point Group	Energy/Hartrees HF/3-21G	Relative Energy/kcal/mol
gauche1		C₂	-231.68772	3.10
gauche2		C₂	-231.69167	0.62
gauche3		C₁	-231.69266	0.00
gauche4		C₂	-231.69153	0.71
gauche5		C₁	-231.68962	1.91
gauche6		C₁	-231.68916	2.20
anti1		C₂	-231.69260	0.04
anti2		C_i	-231.69254	0.08
anti3		C_2h	-231.68907	2.25
anti4		C₁	-231.69097	1.06

Table above from https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3

Comparing the structure of our molecule against those in the chart it is clear that our molecule match up to the gauche2 and anti2. We can also see that the energy values that we calculation are very close to those that have been previously recorded. This suggests that our calculation have yielded the expected results so are reasonably accurate.

We can run the calculation at a higher basis set to get a better result. We will run another calculation on the anti2 comformation but this time run the method as DFT B3LYP/6-31G*. For the log file click here, for the .chk file click here.

Comparing the two structure directly there is very little change as a result of changing the basis set however there is quite a large change in the energy of the molecule, suggesting there has been some changes but the overall shape of the molecule hasn't changed that much. We also ran a DFT/6-31G* for the gauche comformation, in the exact same way we ran it for the anti conformation. For the log file click here, for the .chk file click here.

Final energy of structure Anti 3-21G/6-31G*
3-21G	6-31G*
-231.69253528	-234.61171030

We will now try and run a frequency calculation, a frequency calculation will gives us additional data on the energy of the structure and allow us to compare these energies to known values. It can also be used to confirm that a molecule is realistic by looking at the vibrataional frequencies, if a shown vibrataional frequency is negative then it is not real and cannot exist so a 'real' molecule would have none of these. To run a frequency calculation we will use the 6-31G* optimisation, then run the calculation again but this time change the method to frequency. We will run a calculation for both the gauche and anti from the 6-31G* from before. Anti: for the log file click here, for the .chk file click here. Gauche: for the log file click here, for the .chk file click here.

Final energy of structure Gauche 3-21G/6-31G*
3-21G	6-31G*
-231.69166702	-234.61070764

Final energy of structure Gauche 6-31G*
sum of electronic and zero-point energies	sum of electronic and thermal energies	sum of electronic and thermal enthalpies	sum of electronic and thermal free energies
-234.468205	-234.460939	-234.459995	-234.499097

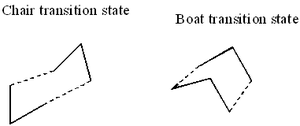
Optimising the chair and boat transition structures

The rearrangement reaction of 1,5 hexadiene goes through either a chair or boat transition state, we will now do calculations on both of these to try and see which one is the most energetically favorable and therefore the preferred transition. The chair and boat transitions state can be modeled as two different CH2CHCH2 very close together. This is because as part of the transition state two of the bonds linking these two fragments hasn't been created yet, so we can model them close together but without the connecting bond to see their energies.

We will create a molecule of CH2CHCH2 in gaussview and optimise it with the method HF/3-21G. For the log file click here, for the .chk file click here. The symmetry label of this group is CS. Using this optimised allyl fragment we can construct the models for the transitions state, in gaussview we made a molecule of two allyl fragments roughly at the right distance and position for the two transition state.

There are several different ways of modelling the transition structure one of these is just to minimize the energy from the geometry we have now, we can tell if the transition state we have is correct by the number and magnitude of the imaginary frequencies that model of the transition state generates. For this calculation then we will run an optimisation and a frequency calculation at the same time so the method will be Opt+Freq with optimisation with Hf/3-21G to a TS(Berny) with force constants calculated once and Opt=NoEigen so the system doesn't crash if we get several imaginary fragments. For the log file click here, for the .chk file click here. If we look under vibrations in gaussview we can see only one imaginary frequency at -818 cm-1 which is exactly what we expected and relates to the cope rearrangement which suggests that our model is quite a accurate representation of the transition state.

Another way we can model the transition sate is by freezing the edge allyl fragments atoms to each other at a their current distance and letting the rest of the molecule optimise around it. Then using the same file and letting the bond length optimise with the rest of the molecule already optimised. For this we will use non optimised molecule and fix the edge atoms bond length to each other then we will run a HF/3-21G optimisation with the option Opt=ModRedundant. For the log file click here, for the .chk file click here. If we look at the log file for this we can see that this molecule closely resembles the molecule from the above calculation suggesting that our cakculations are on track. WE will now use the output file and run another calculation with the method changed to 'derivative'. For the log file click here, for the .chk file click here. The bond distance between the edge atoms are shorter than the ones for the other optismisation but the general structure seems roughly the same.

We can also use the QST2 method to optimise the boast transition structure. In this method you can specify the reactants and the products for the reaction. Since the reaction we are modelling is a rearrangement reaction the products and reactants is the same but we will assign each atom a number so the position of the double and the atoms change within the molecule hence making the reaction a rearrangement. We first created the 1,5 hexadiene molecule in gaussview then we changed the orientation of the molecules so that they appear almost to be cyclic, as to repersent the actual geometry they would have to adopt to do a successful 1,5 hexadiene transition, this comformation is with the middle four carbons having a dihedral angle of 0^o and then C2C3C4 and C5C4C3 angles to be 100^o. The calculation will then be run as an Opt+Freq with the TS(QST2)HF/3-21G. For the log file click here, for the .chk file click here.

While these calculation output allow us to see the transition state but doesn't allow us easily to compare the energies of the transition states however we can use the intrinsic reaction coordinate or IRC method which allows us to find the minimum energy path from a transition structures to the end product. Allowing use to find the most likely transition state, this will be done done by taking one of the optimised from our chair tranisiton structure than running another simulation with the option of computing the reaction in the forward direction and to calculate the force constants at every step and change the number of steps to 50. The comformation we get as the output of this calculation should be the comformation that goes through the lowest energy transition state. For the log file click here, for the .chk file click here. We can see by looking at these output files that the transition state with the lowest energy is the chair transition state.

To confirm this we can take a look at the activation energy for the reaction by doing a 6-31G* optimisation on the chair and boat transition state. We should be able to see the structural and energetic differences between the two. The chair comformation for the log file click here, for the .chk file click here. The boat comformation for the log file click here, for the .chk file click here.

Activation energies are calculated by subtracting the Sum of the Electronic and Thermal Energies for the product molecule from the Sum of the Electronic and Thermal Energies for the transition state.

Final energy of structure Anti 6-31G*
sum of electronic and zero-point energies	sum of electronic and thermal energies	sum of electronic and thermal enthalpies	sum of electronic and thermal free energies
-234.469169	-234.461828	-234.460884	-234.500731

We are expecting the values for the activation energy to be 33.5 ± 0.5 kcal/mol for the chair transition structure and 44.7 ± 2.0 kcal/mol for the boat at 0K. Our results while higher are in the same order of magntiude and show the correct trend and the values roughly the same relative to each other. This suggests that at higher temperatures the activation energy is higher.

Diels alder reaction

We have looked at a variety of tools in gaussian for finding out information of the transition state of a reaction. We will use thewese new found tools in a longer more detailed look at a particular reaciton. IN this case we will be looking at a diels alder reaction (hence the title) of butadiene and ethene. Using the tools above we will take a more detailed look at the nature of the transition state by looking at not pnly the enegry of the reation but also the HOMO/LUMO interactions of the reactants and seeing if a reaction is viable and how it would most likely proceed. For this reaction to happen the HOMO of one molecule the conjugated diene has to donate to the LUMO of the dienophile. In this reaction there is also a symmetry consideration in this reaction as a reaction can only happen between a LUMO and HOMO of the same symmetry in terms of symmetric or anti-symmetric towards the plane of symmetry.

First of all we will start by optimising the reactcants for this we will perform a simple optimisaisation calculation using DF.3-21G on both the butadiene and the ethene molecule. For the butadiene molecules log file click here, for the .chk file click here. For the ethene molecules log file click here, for the .chk file click here. Using these optimisation we can look at the HOMO/LUMO orbitials.

Activation energy of reaction
Structure	Sum of the Electronic and Thermal Energies for the product	Sum of the Electronic and Thermal Energies for the appropriate transition state	Activation energy	Expected value for 0K
Chair	-231.531794 a.u	-231.461340 a.u	44.21 Kcal/mol	33.5 ± 0.5 kcal/mol
Boat	-231.532648 a.u	-231.445301 a.u	54.81 Kcal/mol	44.7 ± 2.0 kcal/mol

We can see by taking a look at the HOMOs and LUMOs that butadiene symmetry is symmetric for LUMO and anti-symmetric for HOMO, for ethene the LUMO is anti-symmetric and the HOMO symmetric . We know that the conjugated diene (butadiene) will have to donate from its HOMO to the LUMO of the dienohphile (ethene) we can see from the MO diagrams that both of these are anti-symmetric, therefore a reaction reacting through this pathway is very conceivable.

Transition state of reaction

To gain a better understanding of this reaction we should fine a model for the transition state, form this we can take a look at the HOMO/LUMO interactions and symmetry as well as the bonds lengths of the molecule, all this should give is additional information on the nature of the reaction and how it proceeds. To do this we placed a butadiene and a ethene molecule close together with the edge carbon atoms around 2.2A apart from their equivalent on the other molecule. We ran calculations at DFT/6-31G* optimisation to a transition state with the edge carbon carbon bonds distance frozen. For the log file click here, for the .chk file click here. The calculation above gives us a fully relaxed molecule apart from the edge carbon carbon bond length has not been optimised so we ran another calculation but this time we ran the optimisation to a minimum, changed the edge carbon carbon bonds from frozen to derivative and never calculate the force constant, all the other options and methods stayed the same. For the log file click here, for the .chk file click here. From the .chk file of the derivative bond calculation we can take a look at the HOMO and the LUMO. We also ran a frequency analysis on the transition state for the log file click here, for the .chk file click here.

HOMO/LUMO orbitals of butadiene and ethene
molecule	HOMO	LUMO
Butadiene
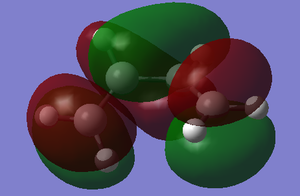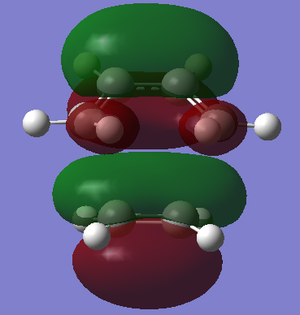
Ethene

HOMO/LUMO orbitals of diels alder transition state
HOMO	LUMO

Clearly both the HOMO and LUMO are symmetric in relation to the plane of symmetry of the molecule. Looking at the different bond the bond length from our simulation are the same as those from literature of the same molecule, the new forming bond is still a long way from forming a new bond. What isn't clear by these numbers as they are only to 2DP is that the C2C3 bond for the diene is slightly shorter than expected for a normal diene C-C bond, this suggests that this particular bond is on the way to forming a a double bond as would expect from this reaction. The frequency analysis reveals a vibration that relates to the reaction path from the transition state to the product, this vibration was at frequency -525cm-1. All the bond making in this vibration is in synch with each other while the fisrt positive virbation is not. The vibration is shown here. Just by looking at these MOs and comparing them to the HOMOs LUMOs of the butadiene and ethene we can find the combination of MOs that these are formed from. By inspection HOMO = k*Ethene HOMO - c*Butadiene LUMO LUMO = k*Ethene HOMO + c*Butadiene LUMO Where c and k are constants determining how much one orbital donates compared to the other. Both the HOMO of the ethene and the LUMO of the butadiene are symmetric so the bonding between them is allowed and hence creating a HOMO and a LUMO of the transition state that is also symmetric.

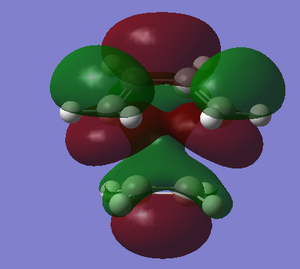Maleic Anhydride and Cyclohexadiene cycloaddition

We will also take a look at the reaction of maleic Anhydride + cyclohexadiene. This is also a diels alder reaction but has two different forms the exo and the endo. We know that the exo form has higher molecular energy. We fist optimsied both products at a 6-31G* level for the maleic anhydride the log file click here, for the .chk file click here. For the cyclohexadine the log file click here, for the .chk file click here. We then placed the two molecule together in gaussview with the atoms that will form in the diels alder reaction about 2.2A apart, we then ran another calculation with the bonds that are to be formed frozen at that distance, in this calculation the optimisation was set to a minimum and the force constant optimised once, the rest of this calculation was done the same method as the individual optimisation. However in this instance there are two possiable conformations the exo and the endo form so one calculation was done for each. For the Endo log file click here, for the .chk file click here. For the Exo log file click here, for the .chk file click here. We then took each of these calculations and changed the changed the bond type between the atoms that will form a bond to a derivative bond and set the optimisation to a transition state and never calculate force constants, the rest of the options for the calculations are the same as before. For the Endo log file click here, for the .chk file click here. For the Exo log file click here, for the .chk file click here. The final set of calculations give us both the endo and the exo transition states. If we take a look at the bond lengths for the endo and exo form there is very little difference in the values. To this level of accuracy they are all identical not giving us any more detail on the nature of the transition state. However if we take a look at the sterics of the transition state we can see that there is alot more steric replusion in the exo form between the CH2CH2 coming off the cyclohexane ring and the three oxygens then there is in the endo form. This is becasusce in the endo form the carbon centers are Sp2 so there is only one hydrogen at 90degrees but in the exo form there are two, where one is pointed towards the oxygen atom, creating a more steric and therefore higher energy transition state.

C-C bond length of diels alder transition state
C-C of edge carbon carbon bonds	Diene C=C (C1C2,C3C4)	Diene C-C (C2C3)	C-C single bond (Lit)^[1]	C=C double bond (Lit)^[2]
2.27A	1.38A	1.41A	1.38A	1.41A

Table of Bond Lengths
Transition State	Forming C-C Bond Separation/Å	Cyclic Diene C=C Bond Length/Å	Maleic Anhydride C=O Bond Length/Å
Exo 6-31G*	1.56	1.34	1.54	1.20
Endo 6-31G*	1.56	1.34	1.54	1.20

References

↑ Lide, D., Tetrahedron, 1962, 17, pp.125-134
↑ Lide, D., Tetrahedron, 1962, 17, pp.125-134

[1] Lide, D., Tetrahedron, 1962, 17, pp.125-134

[2] Lide, D., Tetrahedron, 1962, 17, pp.125-134

[1]

[2]