Computational Chemistry lab Module 2

Using, creating and optimising molecules is gaussview 5

The gaussview 5 program can be used to create molecules and find their most energetically favorable state by using quantum mechanical equations. The programs allows users to simply make the desired molecule and then run QM calculations with a variety of opinions and settings. We can depenstrate this my making a molecule and running claculations on it to find its most optimised state and compare these results with caluclations done with different setting.

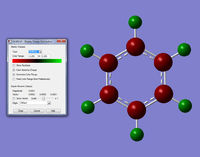
The first thing we done was create the molecule and optimise its energy, this is done by simply making the desired molecule with the element fragment tool, for the optisimation calculation we use the calculation type FOPT, method B3LYP and the basis set 3-21G. For a graphic of this click this link: Optimised BH3 Molecule, for the log file click here.For the optimisation file click here. The results of this optisimation are found in the .log file but they have been tabled here to be easier understood and compared

    
         Item               Value     Threshold  Converged?
 Maximum Force            0.000413     0.000450     YES
 RMS     Force            0.000271     0.000300     YES
 Maximum Displacement     0.001610     0.001800     YES
 RMS     Displacement     0.001054     0.001200     YES
 Predicted change in Energy=-1.071764D-06
 Optimization completed.

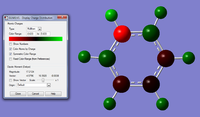
We can make a more defined and accurate model of the system if we higher level basis set, this is changed in the opinions for each calculation, a larger basis set usually gives a more accurate answer but normally takes longer for the optimisation to run. We will run the same optimisation again but this time using 6-31G(d,p) basis set, when we change the basis set we need to remember to but d,p in the options next to the 6-31G tab and add the Nosymm keyword, all the other settings are kept the same. The image is here graphic for larger basis set. For the log file click here. For the optimisation file click here. The results for this optimisation is also tabulated.

BH3 optimisation
Field	Results
B-H bond distance	1.19347A
H-B-H bond angle	119.998
Final energy	-26.42 a.u
Gradient	0.0002067 a.u.
Dipole moment	0D
Point group	D3H
Calculation time	5 minutes

   Item               Value     Threshold  Converged?
 Maximum Force            0.000012     0.000450     YES
 RMS     Force            0.000008     0.000300     YES
 Maximum Displacement     0.000049     0.001800     YES
 RMS     Displacement     0.000032     0.001200     YES
 Predicted change in Energy=-8.912306D-10
 Optimization completed.

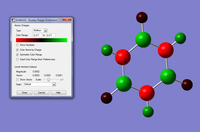
These calculations are very short and not complex calculation, for larger ones we have to run it off Imperial College London's SCAN system. To show this we created a TlBr3 molecule and forced the molecule to keep its D3H symmetry and with a tolerance of 0.0001. We ran the optisimation with settings DFT, B3LYP and with the basis set LanL2DZ, which uses two different basis set one for the heavy molecules one for everything else. This molecule should keep its D3h symmetry, we should also be able to tell how good the simulation of the TlBr3 molecule is by comparing its Tl-Br bond length with literature Values. Graphic for TlBr3. For the log file click here. For the optimisation file click here. The results for this optimisation is also tabulated.

BH3 optimisation (6-31G(d,p))
Field	Results
B-H bond distance	1.19332 A
H-B-H bond angle	120.000
Final energy	-26.61 a.u.
Gradient	0.00000624 a.u.
Dipole moment	0D
Point group	D3H
Calculation time	1.5 minutes

Item               Value     Threshold  Converged?
 Maximum Force            0.000002     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000022     0.001800     YES
 RMS     Displacement     0.000014     0.001200     YES
 Predicted change in Energy=-6.084031D-11
 Optimization completed.

Our value of Tl-Br bond distance is 2.65095A, the literature value we could find puts the bond length at 2.521A ^[1] . While there are some differences in these values, they are quite close especially for a medium accuracy model. If we wanted a better value we could a different basis set to get a more accurate value but the value we have seems good enough for this level of accuracy.

We can make different atoms in the same molecule use different methods of calculation. For example in BBr3 we have three heavy Br atoms that should be treated with a pseudo potential as a full basis set will take too much calculation and the boron atom which requires a full basis set or it doesn't have enough accuracy. In this calculation we will use calculation for the 6-31G BH3 as a base, and change the H atoms to Br our calculation type will be FOPT, RB3LYP. For the heavy bromide atoms we will use the LanL2DZ pseudo potential and for the boron we will use 6-31g(d,P).Graphic for BBr3. For the log file click here. For the optimisation file click here. The results for this optimisation is also tabulated.

TlBr3 optimisation
Field	Results
Tl-Br bond distance	2.65095 A
Br-Tl-Br bond angle	120.000
Final energy	-91.22 a.u.
Gradient	0.00000009 a.u.
Dipole moment	0D
Point group	D3H
Calculation time	0.5 Minutes (run on SCAN)

        Item               Value     Threshold  Converged?
 Maximum Force            0.000008     0.000450     YES
 RMS     Force            0.000005     0.000300     YES
 Maximum Displacement     0.000036     0.001800     YES
 RMS     Displacement     0.000023     0.001200     YES
 Predicted change in Energy=-4.027223D-10

BBr3 optimisation
Field	Results
B-Br bond distance	1.933 A
Br-B-Br bond angle	120.000
Final energy	-64.44 a.u.
Gradient	0.00000382 a.u.
Dipole moment	0.0002D
Point group	D3H
Calculation time	2 Minutes

We now have models of bond length and bond angles for three different molecule (Tl-Br, B-Br, B-H). As we would expect there are significant differences between the bond length in the different molecules. Boron and hydrogen are both small molecules and have good orbital overlap, this would cause the B-H bonds to be quite strong so we would expect there bond length to be pretty small. BBr3 however doesn't have as good overlap this is mostly due to bromide being quite a large molecule, also its orbital overlap with boron isn't very good so we would expect the both to be much weaker and hence longer. However in BBr3 the bromide atoms have lone pairs in the right orientation to donate to the empty boron p orbital, this donation strengthens the B-Br bond. While the donation shortens the B-Br bromide is still a very large molecule and the donation isn't as good as pi bonding is very dependent on distance, which is this case is very large. For these reason BH3 has a very short bond length while BBr3 having a medium bond length which would be longer if not for pi donation. The other significant comparison we can make is between BBr3 and TlBr3, as the only change is a dramatic change in the central atom. We have already talked about BBr3 in this case however there is almost no pi donation to the central atom as the size between the two is very large as both are large molecules especially Tl. The change in size of central atom is the most important factor in this comparison not only does it effect the pi bonding but also makes the sigma bonding suffer as with the other comparison the greater size of the molecules causes large and diffuse orbital. This in turn means that the orbital overlap is much poorer for this molecule and hence the weaker and therefore longer bond.

Frequency Analysis

To confirm that we have have found the structure with the lowest energy we carry out frequency analysis, this tells us if we have the lowest energy set-up of this molecules, also with this information we can make animations of these molecules, also from this we can work out spectral data and compare against literature values for this molecule this tells us if the model is correct. We carry out frequency analysis by changing the settings in the gaussian calculations, instead of doing an optimisation of the molecules the setting is changed to frequency. For a demonstration of this we used the BH3 6-31G optimised log file and changed the calculation setting as above. For the log file click here. For the optimisation file click here.

BBr3 optimisation
Molecule	Bond Length
BH3	1.193 A
BBr3	1.933 A
TlBr3	2.651 A

With the frequencies that gaussview gives us we can show the vibratonal nodes for the molecule. These frequencies and there moment can be viewed through the gaussview program but in terms of displaying them here it is easier just to tabulate them. The frequencies tell us if our molecules is 'on track' for what we expect, generally we consider the first size values to have +/- 25 as a minimum and +/-15 as a good value to have.

 Low frequencies ---  -10.1828   -5.7670   -5.4933   -0.0045    0.0917    1.7554
 Low frequencies --- 1152.4687 1209.4476 1209.4499

BH3 Frequecny analysis
Field	Results
B-Br bond distance	1.933 A
Br-B-Br bond angle	120.000
Final energy	-26.61 a.u.
Gradient	0.00000624 a.u.
Dipole moment	0.0002D
Point group	D3H
Calculation time	2 Minutes

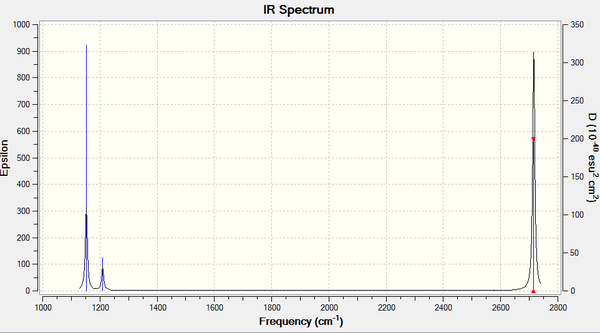
The Ir spectrum of the optimised BH3 molecule. There appears to be only three peaks on the Ir spectrum, this is becausce there are two sets of degenerate vibrations and one vibrations with no intensity, meaning one is no there and two more are identical to two you can see.

We can also use vibrtaional analysis in the same way to take a look at TlBr3, we will compare the results of this to the values of Bh3 frequency analysis. We will use the same optimised file as was created for the TlBr3 optimisation above and change the calculations as before to be frequency. All the other settings for the calculation are kept the same, for more details on these see above.For the log file click here. For the optimisation file click here.

Low frequencies ---   -3.7412   -0.0028   -0.0004    0.0014    3.6276    3.6276
Low frequencies ---   46.4049   46.4051   52.1083

BH3 Frequecny analysis
Number	Description	Frequency	Intensity	Symmetry Form
1	The three hydrogen atoms move one side then the other of the σh plane of symmetry. The Boron is moving in the opposite direction to the hydrogens	1152	93.3	A2
2	Two of the hydrogens atoms move upwards in a concerted effort towards the third then move back down. The boron moves slightly in the opposite direction to the hydrogen motion	1209	13.3	E'
3	Two of the hydrogens move with a fixed bond angle in the σh plane of symmetry while the third moves from one side to the next unalterably what other hydrogen it is closest too. The boron moves opposite to the single hydrogen	1209	13.3	E'
4	All three hydrogens move out then in again at the same time. The boron is stationary	2577	0	A1'
5	One hydrogen stays still while the other two move backwards and forwards, with there positions being 180 degrees out of phase. The boron moves against the motion of whatever hydrogen is moving away from it	2716	135.5	E'
6	Two hydrogens move backwards and forwards in a concerted effort while the third also does the same motion but at a longer distance and 180 degrees out of phase. The boron moves opposite to the single hydrogen	2716	135.5	E'

We can clearly see from looking at these tables that there is a massive difference in the frequency of the vibrations of BH3 and TlBr3. The main reasons for large differences in vibration frequency is either due to bond strength and atom mass. In this situation not only are the TlBr3 atoms much heavier but there is also quite a large difference in bond length which suggests a large difference in bond strength. Therefore it is logical to assume that the molecule which much higher atomic mass will have vibrations at a much lower frequency. Also as mentioned the bond length are much longer for TlBr3 (see above) this means that the frequency will also be lower, hence all the frequencies for TlBr3 aren't even close to those of BH3. In most of the TlBr3 vibrations the movement of the central ion is much larger compared to those of BH3, this is due to the size of the three ligands compared to the central ion i.e. thallium has to compensate more for the movement of the bromine than boron has to do for the movement of the hydrogens as compared to the central ions bromines are heavier. It it also clear looking at the chart of the different vibrations that both TlBr3 and BH3 share some of the same motions and vibrations. This is because the different vibrational movement come from the symmetry, and as TlBr3 and BH3 share the same symmetry the vibrational modes are the same but the energy for each one is different.

TlBr3 Frequecny analysis
Field	Results
B-Br bond distance	2.651 A
Br-B-Br bond angle	120.000
Final energy	-91.22 a.u.
Gradient	0.00001821 a.u.
Dipole moment	0D
Point group	D3H
Calculation time	2 Minutes

The spectra for both of these molecules look reasonably similar in terms of the general shape, this is due to the effect above of them sharing the same vibrational mode. However there is much less defined peaks in the TlBr3 spectrum, this could be down to the number of size of atoms in TlBr3 meaning there is not only one energy where a motion can apply i.e. the energy for a motion isn't as defined as with BH3 where a very defined amount of energy is required for the vibrations to happen.

The Ir spectrum of the optimised TlBR3 molecule. There appears to be only three peaks on the Ir spectrum, this is becausce there are two sets of degenerate vibrations and one vibrations with no intensity, meaning one is not there and two more are identical so you only see three distinct peaks.

The same optimisation and frequency must be used both optimisation and frequency because anything that is a different basis set or method will give dramatically different values and these are not comparable to each other, hence we cannot compare to results with different basis sets. If you start a frequency on a optimised molecule but was optimised with a different basis set the values will be different than for the basis set that we are know running, hence the molecule will not be fully optimised and we will get a wrong value at the end.

We carry out frequency analysis as this gives us additional information on the molecule such as how the bonds moves and so we can compare against known IR spectrums and see if the simulations we have run are comparable to real situations. The Low frequencies are the 3N-6 vibrational frequencies and are just the motion of the central atom and the ones it is bonded to.

MO Analysis

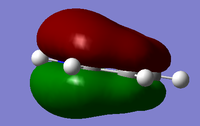
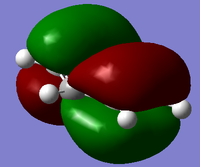
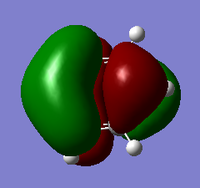
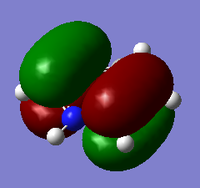
Another useful analytical tool that we can use from gaussian is being able to create and see in 3D the molecular orbital. This is also useful in comparing these calculated MOs to the ones from LCAO. We found the MOs by loading the .chk from the BH3 optimisation, we used this and changing the settings in the calculation to full NBO. When the calculation was run we looked at the first 8 MOs, the first MO was the 1s orbitial but the other seven had their pictures taken and compared against the LCAO orbitial. For the .chk file click here.

This is a diagram showing the MO of BH3 and it clearly demonstrates the similarities between the MOs described by the LCAO and by the gaussian calculations. We can see that in this case the two are very similar in size and shape and are in very strong agreement, no significant differences can be seen between the two sets. Given this similarity we can say that the qualitative MO theory stands up to the test of 'real' data and therefore is a fairly reliable and accurate theory.

NBO Analysis

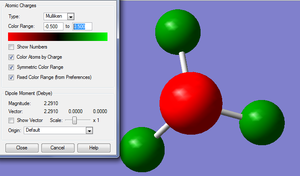
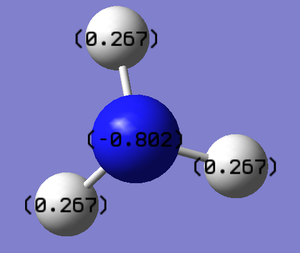
Natural bond analysis is a useful tool also from gaussian to test and show its function we will set one up for a NH3 molecule, however first of all we must go through all the steps we have already done for the molecules above for NH3. We will create the molecule and run an optimisation with the 6-31G basis set, then run a frequency analysis and a population analysis. The .chk file for the optimisation here and the .log file here. The .chk file for the frequceny analysis here and the .log file here. The .chk file for the MO analysis here and the .log file here.

In this example the frequency analysis step has not yielded the ideal range of frequencies, we would usally expect the values for the low frequency to be within +/- 20, in this case they are reasonably close to this range but not exactly inside it, so there is a small doubt over their accuracy but since this exmaple is mainly going to be used as a demonstrastion pf NBO it is fine for its purpose. The usefulness of the NBO analysis is seeing the difference in electron charge across the molecule, this has been demonstrated by the graphs below.

Item               Value     Threshold  Converged?
 Maximum Force            0.000056     0.000450     YES
 RMS     Force            0.000037     0.000300     YES
 Maximum Displacement     0.000144     0.001800     YES
 RMS     Displacement     0.000095     0.001200     YES
 Predicted change in Energy=-1.108753D-08
 Optimization completed.

  Low frequencies ---  -11.6313  -11.5960   -0.0028    0.0243    0.1402   25.5608
 Low frequencies --- 1089.6620 1694.1733 1694.1736

This is a diagram showing the charge distribution of NH3, the colour coding system is described on the right but the interface of gaussian. This clearly see where the charge is located in this system, this generally agrees with chemical knowledge in terms of lone pairs and electronegativity

his is a diagram showing the charge distribution of NH3, the numbering system used is fairly standard with negative values representing a negative charge.

This is a diagram showing the MO of NH3, in this diagram it is slightly harder to compare the LCAO and the gaussian MOs, this is because the NH3 molecule adopts a C3v symmetry so the three hydrogen orbitals are moved closer together. However looking at the chart we can see that most of the orbitals are consistent with the LCAOs there is a slight difference in the degnerate antibonding orbitials where there seems to be more going on in the gaussian MOs than the LCAO, this is becasuce the LCAO model is weaker for more complicated molecules. It seems generally reliable as the LCAO and the gaussian MOs are very similar but in more complicated MOs the LCAO loses accuracy as its quite a simple model.

Association energies

We can calculate using gaussian the association energy of a molecules, we can do this by finding the combined starting energies of the reactant and comparing this against the energy of the product. For this example we will use as the product the compound NH3BH3 not only because we have already done the calculations for both the BH3 and the NH3 molecule with the same method and basis set, but also because NH3BH3 is a interesting molecule with possible uses in a fuel system.

Since we will be directly comparing values of energies from these calculations we have to make sure that they are run all in the same basis set and using the same method as each other or the values for the energies will not be comparable. Since we have already run the BH3 and NH3 optimisations with the 6-31G(d,p) basis set and the methods: DFT, B3LYP it is logical to suggest running the NH3BH3 optimisation with these same setting to reduce the necessary amount of calculations required. As with most of the other examples we have done we will run a frequecny anaqlsysis to make sure the optimisation is at a minimum. The .chk file for the optimisation here and the .log file here. The .chk file for the frequceny analysis here and the .log file here.

Item               Value     Threshold  Converged?
 Maximum Force            0.000132     0.000450     YES
 RMS     Force            0.000037     0.000300     YES
 Maximum Displacement     0.001220     0.001800     YES
 RMS     Displacement     0.000543     0.001200     YES
 Predicted change in Energy=-1.180827D-07
 Optimization completed.

 Low frequencies ---    0.0008    0.0009    0.0015    5.7428   14.9757   20.2781
 Low frequencies ---  263.3588  631.3097  638.0752

The association energy will be the energy of the product minus the energy of the reactants, 1 a.u ≈ 2626 KJ/mol. If we calculate the ΔE or association energy it gives us 420 KJ/mol which is roughly in the range for quite a strong bond as we would expect from this particular molecule. So we can say that gaussian can be used effectively to estimate values for bonds and therefore could be used well in analysis of particular unknown molecules.

TlBr3 Frequecny analysis
Number	Describtion	Frequency	Intensity	Symmetry Form
1	Two of the bromines atoms move upwards in a concerted effort towards the third then move back down. The thallium moves slightly in the opposite direction to the bromines motion	46.4	3.69	E'
2	Two of the bromines move with a fixed bond angle in the σh plane of symmetry while the third moves from one side to the next unalterably what other bromines it is closest too. The thallium moves opposite to the single bromines	46.4	3.69	E'
3	The three bromines atoms move one side then the other of the σh plane of symmetry. The thalium is moving in the opposite direction to the bromines	52.11	5.85	A2
4	All three bromines move out then in again at the same time. The thallium is stationary	163.4	0	A1'
5	One bromine stays still while the other two move backwards and forwards, with there positions being 180 degrees out of phase. The thallium moves significantly against the motion of whatever bromine is moving away from it	210.79	25.5	E'
6	Two bromines move backwards and forwards in a concerted effort while the third also does the same motion but at a longer distance and 180 degrees out of phase. The thallium moves significantly in the opposite direction to the single bromine	210.79	25.5	E'

Investigation into aromaticity

To fully utilise the gaussian program will we take a much in depth look than previous at aromaticity in benzene and benzene like structures. The benzene like structures we will be looking at are benzene, Boratabenzne, pyridinium and borazene. For each one we will optimise with a 6-31G basis set and method of B3LYP, then a frequency analysis ,a population analysis then a NBO analysis, all of these calculations will be done using the same method and settings for the calculation apart from changing the main point of that particular calculation, for example we will change from optimisation to energy when doing the population analysis, if you want anymore information for how these are run look above for the more detailed emxplaes. All of these calculations will be done on the imperial HPC SCAN system and will have links to the calculation results in the Dspace.

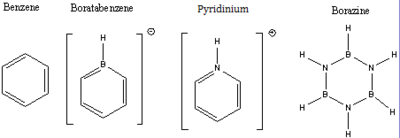
Benzene

For the .fchk file for the optimisation here and the .out file here and for the published data on Dspace click here. For the .fchk file for the frequency analysis here and the .out file here and for the published data on Dspace click here. For the .fchk file for the MO analysis here and the .out file here and for the published data on Dspace click here.

Item               Value     Threshold  Converged?
 Maximum Force            0.000204     0.000450     YES
 RMS     Force            0.000084     0.000300     YES
 Maximum Displacement     0.000870     0.001800     YES
 RMS     Displacement     0.000313     0.001200     YES
 Predicted change in Energy=-4.983462D-07
 Optimization completed.

Low frequencies ---  -14.2262   -2.7299   -0.0008   -0.0006    0.0004   10.0025
 Low frequencies ---  413.7271  414.5532  621.0441

Association energy of NH3BH3
Molecule	Energy (AU)	Energy (KJ/mol}
BH3	-26.61
NH3	-56.56
NH3BH3	-83.22
ΔE	-0.16	420

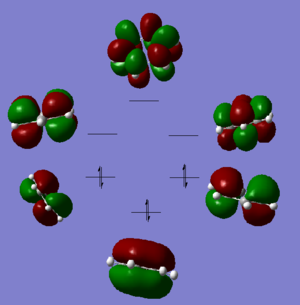
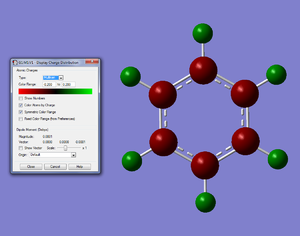
We know the optimisation has worked as it has converged and that the low frequencys are within +/- 15, from this we can say that our virtual molecule is a decent representation of the real thing. If we then take a look at the pi orbitals we can see what we would expect from benzene and these pi orbitals generally agree with the LCAO MOs, this gives further evidence to the reliability of our molecule. Finally the charge distribution is also what we expected with all the carbon atoms being the same charge and all the hydrogens being the same charge with the electrons being more electropositive than the carbon atoms. All these calculations seem to be strong agreement with data from 'real' benzene.

Boratabenzene

Item               Value     Threshold  Converged?
 Maximum Force            0.000159     0.000450     YES
 RMS     Force            0.000069     0.000300     YES
 Maximum Displacement     0.000894     0.001800     YES
 RMS     Displacement     0.000328     0.001200     YES
 Predicted change in Energy=-6.589668D-07
 Optimization completed.

 Low frequencies ---  -14.0387   -0.0008   -0.0007    0.0003    9.5455   14.6725
 Low frequencies ---  371.0132  404.6531  565.1753

For the .fchk file for the optimisation here and the .out file here and for the published data on Dspace click here. For the .fchk file for the frequency analysis here and the .out file here and for the published data on Dspace click here. For the .fchk file for the MO analysis here and the .out file here and for the published data on Dspace click here.

Benzene bond lengths and angles
Field	Results
C-C bond length	1.40A
C-H bond length	1.09A
C-C-C bond angle	120 degrees
H-C-C bond angle	124 degrees

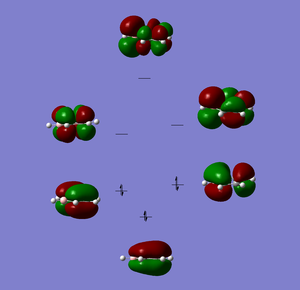
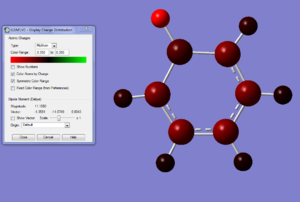
We know the optimisation has worked as it has converged and that the low frequencys are within +/- 15, from this we can say that our virtual molecule is a decent representation of the real thing. If we then take a look at the pi orbitals we can see what we can start to see the effect of adding in the bromine atom, the antibonding MOs have a lot more electron density around the boron atom and vice versa for the bonding MOs. The hydrogen that is connected to the boron is a lot more electronegative than the rest of the hydrogens. In the boratabenzene it appears as though there is no B-C double bonds, the picture looks like this because gaussian says its a double bond when the bond length is below a certain value, in this case it hasnt reached the value need for this to happen, but given the negative charge on the molecule we know there is aromoticity in the molecule and isoelectron to benzene so it is still directly comparable and this lack of a 'double bond' does not reflect on the nature of the molecule.

Pyridinium

Item               Value     Threshold  Converged?
 Maximum Force            0.000056     0.000450     YES
 RMS     Force            0.000020     0.000300     YES
 Maximum Displacement     0.000527     0.001800     YES
 RMS     Displacement     0.000129     0.001200     YES
 Predicted change in Energy=-4.638162D-08
 Optimization completed.

Low frequencies ---   -3.1827   -0.0004    0.0008    0.0009   11.3844   13.8823
 Low frequencies ---  401.5804  413.7095  640.1249

For the .fchk file for the optimisation here and the .out file here and for the published data on Dspace click here. For the .fchk file for the frequency analysis here and the .out file here and for the published data on Dspace click here. For the .fchk file for the MO analysis here and the .out file here and for the published data on Dspace click here.

Boratabenzene bond lengths and angles
Field	Results
C-C bond length	1.41A
C-H bond length	1.10A
C-B bond length	1.51A
H-B bond length	1.22A
C-B-C bond angle	115 degrees
C-C-C bond angle	122 degrees
H-C-C bond angle	120 degrees

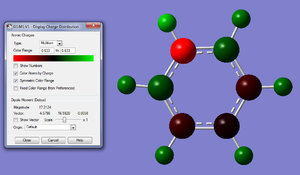
The optimisiation converged and the frequency analysis gave values between +/- 15. The Pi orbitals make sense and seem to be a good representation of the real pi system, we conclude by looking at the way the electronegativity affects bonding and anti bonding orbitals i.e. the most electronegative molecule should have the largest bonding orbitial and smallest anti bonding orbitial which looking at the first Pi orbital we can see that this is true. The charge distribution also seems to repersent what we know of the pyridium molecule, i.e. the electronegativity of nitrogen is having a noticeable effect on the charge of surrounding atoms. All of this goes to suggest that the pyridium calculations are a good representation of the real molecule and that they have a fairly high degree of accuracy.

Borazine

Item               Value     Threshold  Converged?
 Maximum Force            0.000223     0.000450     YES
 RMS     Force            0.000051     0.000300     YES
 Maximum Displacement     0.000492     0.001800     YES
 RMS     Displacement     0.000158     0.001200     YES
 Predicted change in Energy=-1.190510D-07
 Optimization completed.

Low frequencies --- -119.0275  -65.6674  -50.5158   -0.0010   -0.0005   -0.0004
 Low frequencies ---  238.8689  244.7092  443.3174

For the .fchk file for the optimisation here and the .out file here and for the published data on Dspace click here. For the .fchk file for the frequceny analysis here and the .out file here and for the published data on Dspace click here. For the .fchk file for the MO analysis here and the .out file here and for the published data on Dspace click here.

Pyridinium bond lengths and angles
Field	Results
C-C bond length	1.39A
C-H bond length	1.08A
C-N bond length	1.36A
H-N bond length	1.02A
C-N-C bond angle	123 degrees
C-C-C bond angle	119 degrees
H-C-C bond angle	119 degrees

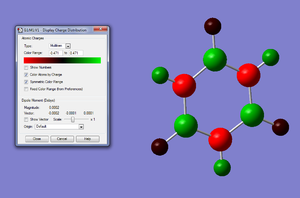
The optimisation for the borazine molecule has converged but the frequency analysis is very far out from what we expected, normally we would throw this result out and run the calculations again however this is the second attempt and the first got roughly the same result. If we take a look at the MOs and the charge distribution graph we can see that they are as we would expect for this molecule, there is nothing in those graphs to tell us that the simulation of this molecule has gone horribly wrong. Given the apparently realistic representation that the data gives and certain time constraints we have decided to continue using the results from this analysis however in this case we will look on any extreme behavior with a degree of skepticism and have a clear idea going into the analysis what degree of accuracy we are dealing with, to borrow a commonly used phase: we will take the results with a pinch of salt.

Charge Distribution

Borazine bond lengths and angles
Field	Results
N-H bond length	1.01A
B-H bond length	1.19A
B-N bond length	1.43A
B-N-B bond angle	123 degrees
N-B-N bond angle	117 degrees
H-N-B bond angle	119 degrees
H-B-N bond angle	121 degrees

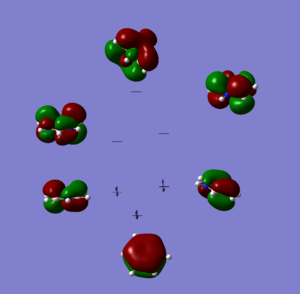
MO Comparisons

Charge Distribution Comparison
[C₆H₆]	[BC₅H₆]^-	[NC₅H₆]⁺	[B₃N₃H₆]

Benzene has the charge distribution as we would expect, the molecule is symmetric so all same atoms have the same charge distribution, the molecule is also neutral charge. The carbons have more charge density than the hydrogens mainly because they are more electronegative and so pull away electron density from the hydrogens.	Boratabenzene is negatively charge overall, hence why all the atoms are electronegative in this graph. The clearest difference between boratabenzene and benzene is that the hydrogen the boron is bonded has more charge density than the rest of the hydrogens (which all have the same charge density) this is because not only is boron less electronegative than the carbon atoms but also the hydrogen itself, so instead of the electron density being pulled away from the hydrogens its being pulled to the hydrogens from the boron. Hence why boron has less charge density than the carbon atoms.	The pyridium ion is positively charged to make it isoelectron to benzene, the nitrogen atom has more charge density than the carbon atoms, this again is due to electronegativity and hence why the hydrogen bonded to the nitrogen has less charge density than the other hydrogens. There is a slight different in the charge density for the carbon atoms at the ortho/meta and para positions. Ortho position has the least charge density mainly due to the electronegativity of the nitrogen atom, then para has the least followed by meta, that last two have different charge densities mainly due to the reasonce forms of benzene, which means the positive charge essentially is distributed around several molecules meaning that none have the same charge density	Borazine doesn't have an overall charge but because of the large electronegativity difference between nitrogen and boron there is a large difference in charge density across the molecule. The nitrogen atoms are the ones with more charge density and the hydrogens bonded to them will have less charge density then those bonded to the borons, the boron atoms will have alot less charge density than the nitrogen atoms and the hydrogens bonded to them will have alot more charge denisty than the borons and the hydrogens bonded to the nitrogens, all of these observations are caused by the electronegativity differences between boron, nitrogen and boron. Overall the borazine is the most polarised molecule, the one with the most dramatic change in charge density.

Pi(1) orbitial
[C₆H₆]	[BC₅H₆]^-	[NC₅H₆]⁺	[B₃N₃H₆]
The 17 molecular orbital in benzene is the first of the pi system orbitals, as a results it is the lowest in energy, this is because there is very little antibonding character in the orbitals but very strong bonding, however when the molecule is no longer symmetric the character of the orbital changes.

We are going to compare everything to benzene in this case, benzene's orbital is completely symmetric and equal at every atom with a very strong bonding character, hence is very low in energy. However if we look at the boratabenzene the orbital is no longer symmetric, this is also true for pyridinium but in boratabenzene the orbital is skewed away from the hetroatom while in pyridinium it is skewed towards it, this is again due to electronegativity where in bonding orbitals more electronegative atoms have a larger orbitals, so while it appears the orbital is skewed away from boron, the boron atom just has less of orbital. Borazine also being made of atoms of varying electronegativity have a skewed nature but in this case because the entire ring is made out of alternating nitrogen/boron the orbital is large then small then large etc, this while symmetric has less axis of symmetry, benzene orbital would have six lines of symmetry while borazine would only have three i.e. its easy to tell where the nitrogen are in borazine as they are under the part of the orbital that appears to stick out the side.

The HOMO
[C₆H₆]	[BC₅H₆]^-	[NC₅H₆]⁺	[B₃N₃H₆]
The HOMO orbital is the 17th orbital and gives a good idea about the how the molecules change with the introduction of different atoms as it is a filled orbital so any change in the orbitals will be directly felt.

The HOMO for benzene is very well defined with the molecule divided in to two sides with the orbital flipped in the plane of the molecule for each one, in this orbitals there is a of bonding and of orbital overlap though it does have quite a lot of anti bonding character which can be seen how close the orbitals of different phase get to get other. If we turn to look at the other three apart from a shape different for boratabenzene and for borazine there doesn't appear to be much difference, we can see a slight effect of difference in electronegativity in borazine and boratabenzene but it isn't particularly strong. The shape for boratabenzene and borazine is slightly different with there being one larger side to the orbital and one smaller side, this is most likely caused by the different sized orbital of the boron in boratabenzene allowing one orbital to be stronger than the other and so take up more room. Apart from this slight shape difference caused by the orbital of the heteroatoms all the HOMO orbitals are remarkably similar, the exact cause of this we could no decide however it could be we just overestimated the effect of heteroatoms to the orbital of the HOMO.

Substitutional effects

We can now take a more qualitative look at the effects of substitutions and the effect of heteroatoms in aromatic systems. The observations we make have all come from the data collected in this work either directly or indirectly.

The LCAO contributions to the MOs

The LCAO for benzene is very simple due to the few types of atoms in the molecule, this means the LCAO are stronger and better for benzene than for any of the other molecules. As we start to introduce heteroatoms and atoms of different electronegativity we start to get a disruption in LCAO. This is due to the electronegativity difference in the molecules making the orbital overlaps less strong and hence reducing the LCAO contributions to the MOs, so the stabilisation effect of the bonds is reduced the more substitutionss we make to the aromatic system.

The energy of the MOs

The overall energy of any these molecule will be determined by the orbital overlap, if one molecule has really strong orbital overlap then it will be much lower energy than one in which the orbital overlap isn't strong or if there a strong anti bonding character. If we look first an benzene we can see very strong orbital overlap mainly due to the regular orbital size and the symmtery of the molecule, however looking at the fully bonding p orbital above boratabenzene has much less overlap between bonding orbitals than benzene, this is mostly due as mentioned to the electrostatic effect of adding heteroatoms to the aromtaic molecules. The same is also true for pyridinium where the orbital overlap is not as strong as for benzene due to the larger hole in one side but isn't as bad as boratabenzene. Generally then adding heteroatoms to the aromatic molecules reducing the orbital overlap by disrupting the orbitals therefore reducing the energy. For borazine the picture is different there is a increase in the energies of the MOs caused by less stabilisation by the bonding orbital this is due to the difference in electronegativty between nitrogen and boron compared to carbon-carbon bonds.

The degeneracy of the MOs

Benzene has many degenerate orbitals because all the atoms in the ring have the same energy and electronegativity so none of the molecular orbitals are being warped by heteroatoms, also all the carbons atoms in benzene are the same so the different orbitals levels all meet up nicely and are degenerate. When heteroatoms are added to this it not only disrupts the symmetry of the molecule making two orbitals that were degenerate no longer degenerate but also the energy of the orbital for each atom is lightly different due to the imbalance caused by the introduction of a heteroatom hence there is a break down of degeneracy. Borazine does not come under this category and its a completely different molecule with several axis of symmetry meaning that even though borazine is made up of as many different types of atoms as pyridinium or boratabenzene it will have more degeneracy as it is arranged more symmetric and hence more degenerate energy levels, however it will still have less than benzene as benzene has a lot more symmetry and less different types of atoms and hence less electronegativity difference.

References

↑ Julius Glaser and Georg Johansson, Acta Chemica Scandinavica A, 1982, 36, pp 125-135 DOI:10.3891/acta.chem.scand.36a-0125

The fully bonded p orbital
[C₆H₆]	[BC₅H₆]^-	[NC₅H₆]⁺	[B₃N₃H₆]
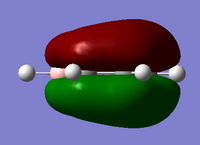
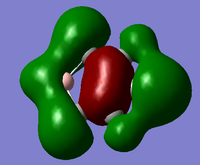
Since we have looked at two pi system orbitals it makes sense to look at a sigma orbital, by far the easiest orbital to identify is the fully bonding orbital for an image of this file click here. This orbital was the 12th orbital so far lower in energy than the other too mainly due to the very good orbital overlap as seen in the diagram.

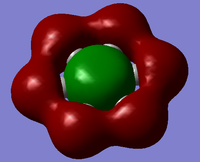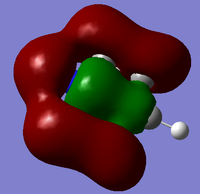Benzene is the perfect 3D representation of the LCAO from the diagram above, clearly having six orbitals all coming from one of the carbon atoms with a very strong bonding profile inside and outside the ring, the overlap of the orbitals that are inside the ring especially strong. However if we look at the boratabenzene where they isn't complete symmetry we start to get distributions to the large bonding ring, we know from the charge distribution graph that the carbon atoms bonded to the boron are more electronegative so we would expect them to have a larger orbital which they do, however we can also see the carbon para to the boron has a much larger electroneagtivity than both of these, this is mainly due to the reasonce forms of benzene so the negative charge can pass to different carbons and resides mostly on the para position, this all leads mostly to the disruption of the outer bonding ring of the orbital leading to less bonding outside the ring but more on the inside of the ring. We would expect a similar thing to happen to the pyridinium orbital expect the nitrogen will have a much larger orbital than the carbons, this much is represented in the MO diagram. However in this orbital all the carbons apart from the para position have a similar orbital sizes making the outer bonding ring much stronger than in boratabenzene and more benzene like, but the carbon in the para position has almost no orbital this could be put down to the lack of charge density at that atom as seen in the charge distribution graph. By far the most different from benzene borazine has a very strange orbital, this again is due to the electronegativity differences in the substituent atoms which is much more dramatic in borazine than any of the other molecules, this leads to very uneven bonding across the molecule and a very strange orbital shape. If we look at the orbital we can see that the nitrogen atoms seem to have small orbital while the boron atoms seem to have very large orbital this is the opposite of what else we have seen in this set of orbital, it almost appears to have some antibonding character in the orbital but it could just look that way due to the very strange orbital and the effect of electronegatvity.

[HR2-1] Julius Glaser and Georg Johansson, Acta Chemica Scandinavica A, 1982, 36, pp 125-135 DOI:10.3891/acta.chem.scand.36a-0125

[1]