Rep:Mod:ts314

Y3C - Third Year Computational Laboratory: Transition states and reactivity

Rinne Cheung (CID:00931629)

Introduction

Molecules are in the minimum when they are in their stable conformer. Gaussian optimises molecules to their minimum in their conformers. It uses quantum machanics to calculate total energy of a molecule including internuclear repulsion energy, as a function position of the nuclei of energy because any Change in location of nuclei in a compound also induce the change of electronic distribution and results in the overall energy change. Potential surface (PES) is a 3D plot where energies against the coordinate of nuclei of compound and it is generated from the Born-Oppenheimer approximation. In terms of PES, minimum is the lowest point in the plot with zero gradient and positive second divertive. Whereas transition state is in the maximum point of the PES with zero gradient but the second divertive is negative, and the conformer is in the highest energy. Therefore compounds with a negative imaginary frequency after optimisation reveals it is in their transition state.

Nf710 (talk) 18:27, 3 November 2016 (UTC) You have a lot of confusion in the paragraph. What you are saying about charge distribution doesn't really make. HF based methods calculate the energies as functions of nuclear and electronic position. DFT based methods calculate the energy as a function of charge density. The born Oppenheimer approx is used in all of these. And The PES is an N dimensional 'surface' of N degrees of freedom.

Exercise 1 - Reaction of Butadiene with Ethylene

Reaction Scheme

(Figure 1, Reaction scheme of Diels-Alder reaction between butadiene and ethylene)

Molecular orbitals

Orbitals that are in the same symmetry can interact and overlap, for example ungerade -ungerade interactions and gerade-gerade interactions are allowed with overlap integral non-zero. Whereas gerade-ungerade interactions are forbidden have a zero overlap integral. From figure 2, HOMO and LUMO of fragment orbitals in the same symmetry overlap and form the MOs of transition state. Furthermore, Woodward Hoffmann rules state that for a ring closure to take place in pericyclic reaction, the electronic barrier should be low in order and the orbital symmetry has to be conserved. In a [4+2 cycloaddition], the ground-state pericyclic change is symmetry-allowed when the total number of (4q+2)_s and (4r)_a components is odd

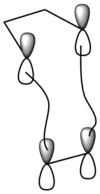
(Figure 2, WH of [4+2cycloaddition])

(Figure 3 MO diagram for DA reaction)

Nf710 (talk) 18:38, 3 November 2016 (UTC) Your bottom MO is wrong

The HOMO of ethene as calculated with PM6

The LUMO of ethene as calculated with PM6

The HOMO of butadiene as calculated with PM6

The LUMO of butadiene as calculated with PM6

The HOMO (u) of the transition state structure of the reaction of ethene with butadiene as calculated with PM6

The HOMO (g) of the transition state structure of the reaction of ethene with butadiene as calculated with PM6

The LUMO (u) of the transition state structure of the reaction of ethene with butadiene as calculated with PM6

The LUMO (g) of the transition state structure of the reaction of ethene with butadiene as calculated with PM6

C-C bond length

(Figure 4, Reactants, TS and product, calculation ran at PM6)

(Figure 5, reaction coordinate of Diels-Alder reaction)

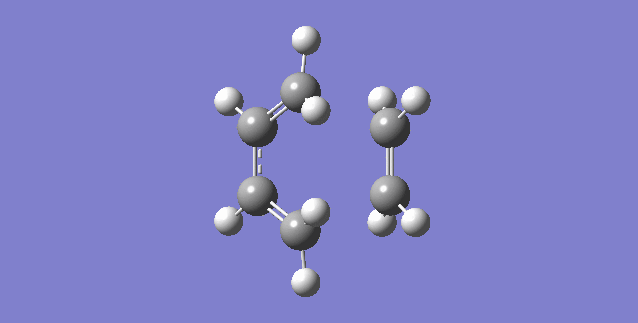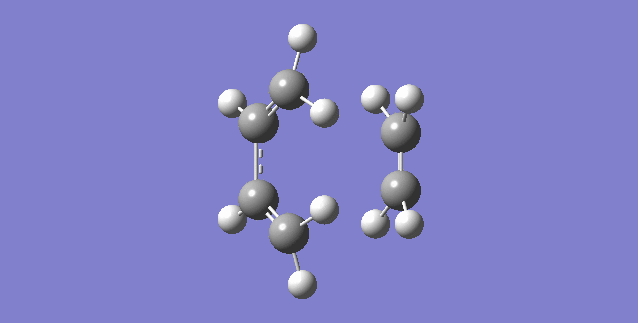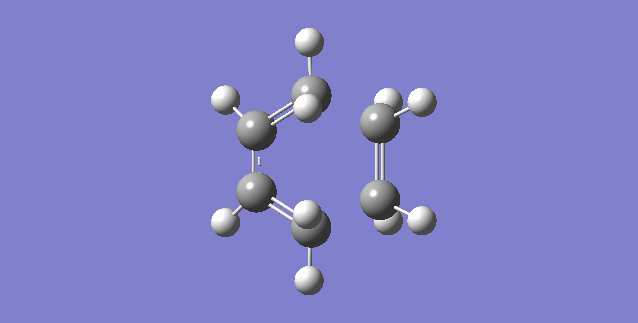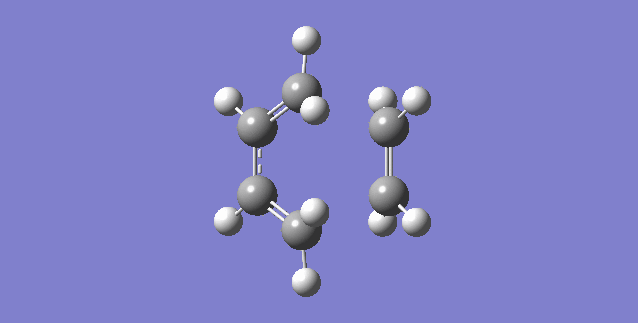
Figure 4 shows the change of bond length when the reaction proceed. The green line (C7-C1 and C2-C13) shows two reactants approach to each other, the distance of the carbon decrease and finally form a C-C single bonds Compare the C-C bonds from the experimental results and typical bond length, which are sp3-sp3: 1.54 Å, sp3-sp2:1.50 and sp2-sp2: 1.47.

Van der Waal's radius of carbon is 1.70Å, but from the Gaussian calculation, C1-C7 and C2-C13 have distance close to 2Å, which is closer then expected (3.4Å)

Bonds in both butadiene and ethene are shorter than the typical values. During the transition state, there were change in bond length, the double C-C bonds in the reactants lengthen whereas the single C-C bonds shorten from 1.468 Å to 1.368 Å. The C-C single and double bonds in product (cyclohexene) are comparable to typical carbon bonds, which are sp3-sp3: 1.54 sp3-sp2:1.50.

C-C bond length (Å)
	Reactants	Transition state	Product
C1-C2	1.312	1.447	1.541
C12-C13	1.335	1.429	1.500
C12-C10	1.468	1.368	1.338
C10-C7	1.335	1.429	1.500
C1-C7	N/A	1.967	1.540
C13-C2	N/A	1.967	1.540
(Table 1, bond length of reactants, transition state and product in Diels-Alder Reaction)

(Figure 6, Animation of Diels-Alder Reaction between butadiene with ethylene)	(Figure 7,Vibration corresponds to the reaction path as tranition state)

The frequency of the first mode is negative (-949 Hartree) and correspond the reaction is at transition state. From figure 6, bond formation is in synchronous, meaning the formations of C-C single bonds occur at the same time. Compare this value to the lowest positive frequency, +145 in the second mode, the vibration is a twist and does not make a significant contribution to the formation for transition state nor a transition state towards the formation of product.

Nf710 (talk) 18:51, 3 November 2016 (UTC) Hartree is the unit of energy. the vibrations are in wavenumbers

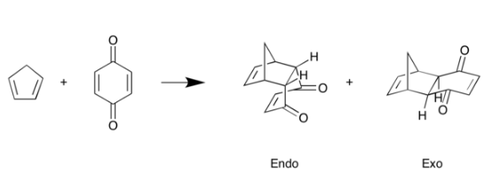
Exercise 2 - Reaction of Benzoquinone with Cyclopentadiene

Reaction Scheme

(Figure 8, Reaction scheme of benzoquinone with cyclopentadiene)

Location of HOMO and LUMO of endo and exo transition state

HOMO(L) and LUMO(R) of transition state
Exo TS	Endo TS

A normal demand Diels-Alder reaction is the reaction between electron rich diene and electron deficient dienophole. There are two electron withdrawing oxygens in the dienophile so the C=C double is more electron deficient. As a result, this is normal demand Diels Alder reaction. However The reaction is less favourable compare to the DA reaction in exercise 1 because the energy of the HOMO and LUMO of the dienophile will be lower in energy due to the lower electron density in the reactive site. From the orbital below the HOMO, it has the symmetry of ugerade,

(Have you proved that the reaction is less favourable? You need to provide data (barriers, reaction energies) for exercise 1 to make that statement. The symmetry of the HOMO-1 is gerade, so I don't know if that's a typo. It's sometimes difficult to see what's going on in the images of the MOs due to the angle you have chosen Tam10 (talk) 17:22, 25 October 2016 (BST))

The MO below the HOMO(L) and the MO above the LUMO(R) of transition state
Exo TS	Endo TS

Nf710 (talk) 17:53, 4 November 2016 (UTC) Great showing the secondary orbital overlap in the endo

Corrected energies

The sum of electronic and thermal Free Energies (Hartree)
	Cyclopentadiene	Benzoquinone	Product	Transition State	Reactants	Energy barrier	Reaction Energy
Exo	-194.045	-381.403	-575.448	-575.400	-575.417	0.0481	0.0307
Endo				-575.381	-575.426	0.0667	0.0217
(Table 2, Values of the sum of electronic and thermal Free Energies, calculation ran at DFT)

A kinetic product form via a reaction path with the lowest energy barrier whereas a thermodynamic product is the most stable conformer formed from the same reactants. In the reaction of benzoquinone with cyclopentadiene, endo product has the lowest energy barrier therefore it can be conclude that it is a kinetic product. It can be explained by the HOMO diagram in figure 10, there are more interaction in the endo transition state. This secondary orbital interaction in LUMO of endo transition state provides an extra interaction in the reactants therefore lower energy is required to form the transition state. On the other hand, exo product is the thermodynamically favourable product because it is the larger reaction energy, meaning there is a greater change in energy between reactants and product and the energy of the exo product is lower and more stable then the endo product.

Nf710 (talk) 17:59, 4 November 2016 (UTC) I am slightly confused to how you have calculated the energies. Firstly you have contradicted your self with what you have said. Also it looks like have made a typo with reactant and products. in the table. It looks like your exo is correct. But for both your endo TS and Products are the wrong energy and hence you get the wrong conclusion. this is a shame and it is a well written section.

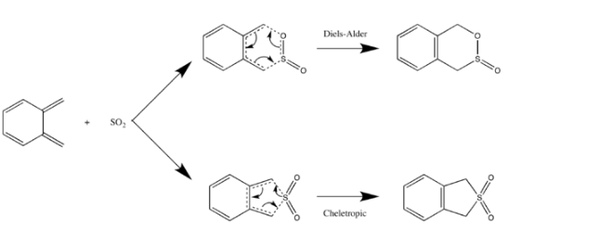
Exercise 3 - Diels-Alder vs Cheletropic for xylylene-SO2 Diels Alder Cycloaddition

Reaction Scheme

(Figure 11, Reaction scheme of exercise 3)

(Please add references when images aren't your own, even if it's from the lab script Tam10 (talk) 17:48, 25 October 2016 (BST))

intrinsic reaction coordinate

Exo Diels-Alder Reaction
Backward Diels-Alder Path of Exo product	IRC calculation of Exo Diels-Alder reaction

Endo Diels-Alder reaction
Forward Diels-Alder Path of Endo product	IRC calculation of Endo Diels-Alder reaction

Cheletropic Reaction
Cheletropic Path	IRC calculation of cheletropic reaction

Energy Profile

The sum of electronic and thermal Free Energies (Hartree)
	Xylylene	SO2	Reactants	Transition State	Product	Energy barrier	Reaction Energy
Exo DA	0.177971	-0.118614	0.05933	0.092077	0.021660	0.032747	-0.03767
Endo DA				0.090560	0.022522	0.03123	-0.036808
Cheletropic				0.099061	0.000117	0.039731	-0.059213
(Table 3, Values of the sum of electronic and thermal Free Energies, calculation ran at PM6)

(Convert energies to kJ/mol. You've taken the reactants to be at infinite separation. They will lose energy as they approach each other so the reactants' energy should be lower Tam10 (talk) 17:48, 25 October 2016 (BST))

(Figure 12, reaction profile)

(This is a pretty funky looking RC. Why not draw dotted lines between the energy levels? The idea was to place (qualitatively) and compare the different reactions in one graph for ease of reading Tam10 (talk) 17:48, 25 October 2016 (BST))

The reactions between xylylene and SO₂ are exothermic and have negative reaction energy. xylyene is extreme unstable therefore it has a high free energy. This energy profiles are in agreement with the IRC coordination. . Furthermore, at low temperature, the formation of endo product is kinetically favourable whereas cheletropic product is a thermodynamically favourable product and will be formed when sufficient energy is provided. As mentioned above in exercise 2, endo product kinetically favourable because it has the lowest activation energy, and cheletropic product is TD favoured because it has the lowest product energy and therefor the greatest stability. The C-C bond 6-member ring product is benzene like and form resonance, meaning the there is a formation of electron pi cloud and the electron in the pi orbital of the carbon delocalise across the 6-member ring

Conclusion

Carbon bond lengths change when then reactions proceed in Diels-Alder reactions and in the transition state, carbon atoms are closer then the Van der Waal’s radius. And the carbon bond formations in exercise 1 take place at the same time, i.e synchronous. Orbitals in the same symmetry can overlap and interact and have non-zero orbital overlap integrals.

Endo product in Diels-Alder reaction is kinetically favoured because the secondary orbital interaction provides extra stability to the formation of the transition state. However, the kinetic transition state can go backward and from a more stable thermodynamic product when extra energy is provided to overcome the higher activation energy barrier. When there are electron withdrawing group in dienophile, the electron deficiency increase the stability of the molecules. But the reaction is less favourable because the energy difference between HOMO and LUMO of the reactants are larger and they will be harder to interact.

Transition states supposed to have the maximum energy as the reaction proceed. However, using Gaussian at PH6 does not provide accurate results to obtain the correct energy of the transition state, and the inaccuracy lead to the reactions having reaction profiles with energy of product higher then the energy of their transition states. It suggests that using DFT method to obtain a more reasonable results.