Rep:Mod:tryingtoCope

Introduction

This experiment is about looking at transition states as well as optimised structures. Transition states are calculated by solving the Schrödinger equation and scanning the potential surface. Activation energy as well as reaction paths can also be calculated using this method.

References to appendix is found here

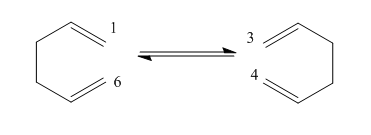
The Cope Rearrangement Tutorial

The aim of this experiment is to calculate the minimum energy structures, transition state structures and the preferred reaction scheme.

The mechanism of this reaction has been subject to much debate but it is now considered to be a concerted reaction with 2 possible transition states. The transition states are either a 'chair' conformer or 'boat' conformer. The chair conformation is considered to be a few kcal/mol lower on energy. When calculating the energy of these states, the B3LYP method with a basis set of 6-31G is considered to have results that are in good agreement with experimental values.

---

Optimisation

Reactant and Product Optimisation

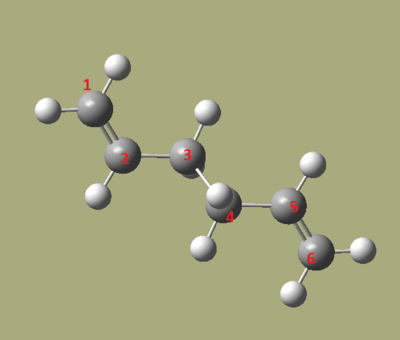
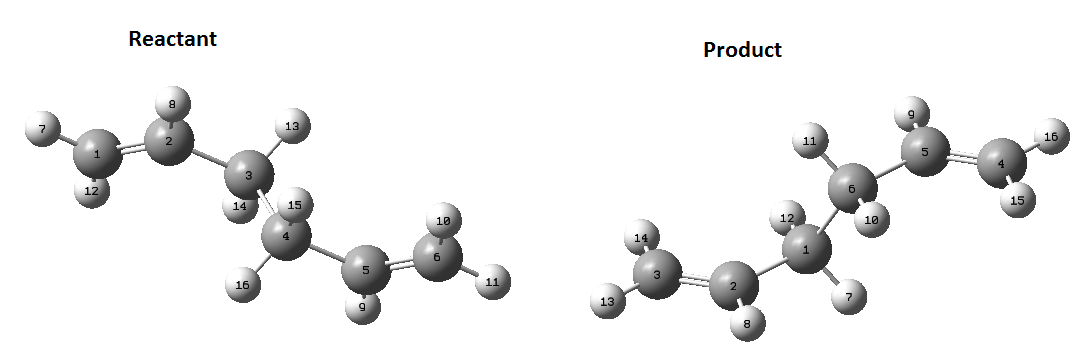
The first step is to draw, in Gaussview, 1,5-hexadiene with the 4 central carbons in an anti-periplanar conformation. Then use the 'clean' command in Gaussview to tidy up the structure. It is important to note that when making a double bond in Gaussview, to remove a hydrogen off the corresponding carbon atoms or the optimisation will remove the double bond added. The optimisation method is the same as the one stated above and was run on Gaussian. The optimisation did the produce the desired optimised structure the first few attempts, but eventually the wanted structure was achieved. Once complete, the checkpoint file was opened and this contains the data Gaussian calculated. In the 'Summary' option, key information is displayed about the calculation. The final energy of this calculation is: -231.6909 Hartrees. The Point group given for this molecule in the summary was C1. Link to file: Media:REACT_ANTIdan.LOG

Gauche 6

Anti 4 in appendix

The gauche conformation of the four centre carbons was then drawn and optimised using the same method. The final energy was -231.6892 Hartrees and no point group was given. Again, after using the symmetrize option, the point group became C1. Link to output file: Media:REACT_GAUCHEdan.LOG

Gauche 6

Gauche 6 in appendix

Low Energy Conformations

The next task was to find the lowest energy conformation. If we consider sterics and van der Waals forces, an anti structure would be the lowest in energy since the chain is not long enough for the gauche structure to have the benefits of attractive van der Waals forces. If rearrange all the carbon atoms to be antiperiplanar to each other, the van der Waals repulsion force is reduced .

Energy: -231.6891 Hartrees (Anti 3) Media:REACT_ANTI3dan.LOG

Gauche 6

Energy: -237.6927 Hartrees (gauch 3) Media:REACT gauche3dan.log

Gauche 6

Anti 2 Conformation: Optimisation and frequnecy

The anti 2 conformation from appendix 1 was draw and optimised using the Hartree-Fock setting and a basis set of 3-31G. Initially, the symmetry of the molecule in .chk file was not correct, indicating the anti 2 conformation was not found. Then, I decided to draw the molecule in ChemBio3D Ultra as there is alot more control over the molecule conformation. The optimisation was carried out gain and the following energy was obtained:

Energy: -231.6854 Hartrees (Anti 2: Point Group - Ci)

The optimisation was run again but with DFT selected, the method was B3LYP and a basis set of 6-31G.

Energy: -234.5535 Hartrees (Anti 2: Point Group - Ci)

The next step is to see if a true minimum has been found and not a transition state. A vibrational analysis was run using the same method and basis set as for the final optimisation above. However, the results of this frequency produced two negative vibrational frequencies which shows this is not a minimum. The optimisation process had to be begun again. Using the same starting point from the ChemBio3D Ultra molecule, the optimisation setting were changed slightly. The Force Constant calculation was changed to once and in the additional key words bar 'opt=noeigen' was added. Now, the optimised structure was still incorrect. So the Calculate force constant was changed to always and the job type was changed to optimise and do a frequency analysis, just to confirm if we have found a minimum not transition state again. Yet again, this failed, there was one negative frequency and the molecule was not the Anti 2 conformation. Since this process keeps failing, a new technique was used. The negative frequency was selected and a manual displacement was set. Because we were essentially at a transition state, what I have now done is modify the structure to move off the peak to change the structure symmetry and energy, so it is now no longer on the peak but to one side of it. So if we optimise this structure, the calculation will follow down the potential energy surface and find a minimum. This still brought back the wrong conformation as Anti 4 was produced again.

I decided to go back to the original input molecule and look for solutions there. I noticed that both C=C bonds kept pointing in the same direction when optimised even though they were in the same plane. So I modified the molecule so one was pointing in and the other out of the screen. Success finally came and the correct molecule was found! The energy with the basis set 3-31G and H-F method was -231.6925 Hartrees and the energy for the 6-31G basis set, DFT and B3LYP method was -234.5997 Hartrees.

Ci molecule: 3-31G and H-F	Ci molecule: B3LYP/3-31G
Molecule 10.2	Molecule 10.5

To compare the structures, I looked at bond lengths and dihedral angles. The dihedral angle of the end 4 carbon atoms was measured and the length of the bonds between these carbons.

Table 1: Comparison data

	Dihedral angle of end carbon atoms/degrees	C=C bond/ Å	C2-C3/ Å	C3-C4/ Å
HF/3-21G	114.64	1.32	1.51	1.55
B3LYP/6-31G	118.74	1.34	1.51	1.56
Literature Values		1.34	1.51	1.54

The energy value produced from both calculations are different, with the B3LYP/6-31G energy being lower. Since these are two different methods, these cannot really be compared. The dihedral angle of both methods shows a variation of 4.1 degrees, the more accurate method having the larger angle. All the bond lengths calculated do match the literature values very well. The C=C bond length of the B3LYP/6-31G method matches exactly and so does one of the C-C bond lengths.

The frequency analysis was carried out on the B3LYP/6-31G optimised structure and produced all positive frequencies, hence the correct minimum energy structure was found. Here is a list of Thermochemistry values obtained from this calculation:

Table 2: Thermochemistry Data from Anti 2 Vibrational analysis

	Description	Value at 298.15K (Unit: Hartrees)	Value at 0K (Unit: Hartrees)	Difference (Units: Hatrees)	Difference in kJ/mol
Sum of Electronic and Zero-Point Energies	Potential energy at 0 K including the zero-point vibrational energy E = Eelec + ZPE	-234.416265	-231.539070	-2.877195	-7554.08
Sum of Electronic and Thermal Energies	Energy at 298.15 K and 1 atm E = E + Evib + Erot + Etrans + Eelec	-234.408962	-231.539070	-2.869892	-7534.90
Sum of Electronic and Thermal Enthalpies	Additional correction for RT H = E + RT	-234.408017	-231.539070	-2.868947	-7532.42
Sum of Electronic and Thermal Free Energies	Entropic contribution to the free energy G = H - TS	-234.447924	-231.539070	-2.908854	-7637.20

To calculate the 0K values, I had to go into the input file, and add the new temperature and pressure, including the mass of all the atoms. The temperature had to be 0.0000001 since 0.0 fails and just calculates the values for 298.15K

When the temperature is changed to 0K, the thermal contribution to the sums is zero, therefore the difference between the two values is the electronic contribution to each calculation.

---

Transition States

TS Berny

There are 2 possible transition states for this reaction and both are made of two C₃H₅ subunits. One transition state has a point group of C_2h and is the 'chair' transition state. The other has a point group of C_2v and is the 'boat' transition state.

The allyl fragment (C₃H₅) was drawn in Gaussview and optimised using the H-F method and a basis-set of 3-31G (which is used in all the calculation below, unless stated). The optimised molecule was then copied twice into a new gaussview molecule window and arranged into the correct geometry of the 'chair' transition state. These was approximately 2.2Å between the 2 subunits and this is a guess at the possible structure. It is much more difficult to optimise transition states than a normal optimisation.

The first step is to compute the Hessian (force constant matrix) which needs to be updated as the optimisation process is continued. If the guessed structure is not close to the actual transition state, then the calculation may fail as the curvature of the potential energy surface is unknown and the calculation may not be able to reach the desired transition state. The reaction co-ordinate can be frozen (keywords: Opt=ModRedundant) which would not make it necessary to calculate the Hessian for the entire molecule, only along the reaction co-ordinate to give a reasonable prediction for the initial force constant matrix.

The guessed molecule was copied into a new window, and an optimisation and frequency calculated. The same method and basis set for optimisation the allyl fragment was used, however a couple changes were made. The 'calculate force constant' option was changed to once, the optimisation was changed to optimise to 'TS (Berny)' and the keywords 'opt=noeigen' was added. The 'opt=noeigen' setting prevents the calculation from crashing if more than one imaginary frequency is obtained. The output file contained a the correct transition state and, as expected, there was an imaginary frequency around 800 cm^-1.

Frozen Coordinate

The guessed structure was also optimised using a different approach. This time the frozen co-ordinate method was used. Once the guessed transition state was copied into a new window, Redundant Coord Editor was selected in the Edit menu and then 'Create a New Coordinate' clicked. This then displayed Add Unidentified (?, ?, ?, ?), and the two terminal carbons where the reaction would take place were highlighted, then 'bond' was selected in the Redundant Coord Editor and 'freeze coordinate'. A new coordinate was created again and the other terminal carbons selected and the same settings chosen. The bond lengths of these frozen coordinates are set to 2.2Å. If this was successful, 'Opt=ModRedundant' should show in the keywords bar when the optimisation calculation is selected. Now the file is ready to be run. Note that we are optimising to a minimum here and not calculating the force constants.

Once completed, the .chk file was opened and it looks similar to the previous optimisation. The bonds that were frozen now need to be optimised. The Redundant Coord Editor was opened again and this time, bond was selected again and derivative was chosen instead of freeze coordinate. This was done for the same terminal carbon pairs. When this calculation is run, we are calculating to a transition state, so TS (berny) is selected, calculate force constant once and opt=noeigen was put in the additional key words.

Comparison

Table 3: Comparison of Optimisation methods using the chair transition state

	Optimised with TS (Berny)	Optimised with frozen coordinate method
Optimised TS Structure
Terminal C-C bond length/ Å	2.02	2.02
Energy/ Hartrees	-231.619	-231.619
Imaginary frequency (cm-1)	-818	-818
Animation

Looking at the table above, there is little, if not, no difference between the two transition states calculated. the energies are the same, the terminal bond lengths are the same and the imaginary frequencies are the same. The image of the imaginary frequencies show that the bond making/breaking in this reaction are concerted. As one bond forms at one end, the other breaks at the opposite end.

Boat transition state optimisation

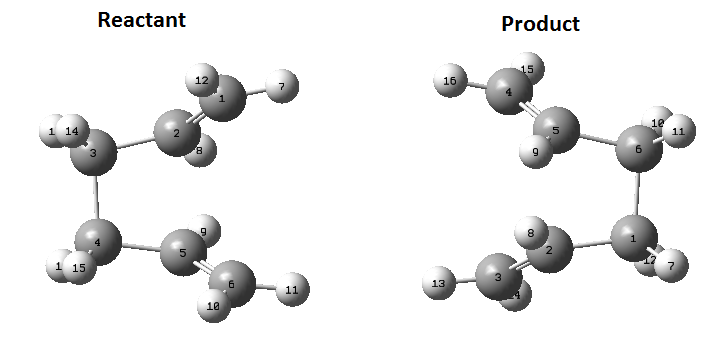
Again, another method was used to calculate this transition state, the QST2 method. In this method, the reactant and product are specified and the method looks for the transition state between them. The reactant and product need to have the same labels otherwise the calculation will fail as it will try and swap hydrogen/carbon atoms to get to the transition state and it will not be pretty. The optimised Anti 2 molecule made earlier is the molecule used for this calculation. Once opened in a new window is needs to be copied again but this time by using 'Add to MolGroup'. 2 of the same molecules will now appear in the same window but in two different 'subwindows'. There are then arranged and labelled using the 'atom list' so they look like the following:

Bond breaking/forming at 1-6 and 3-4

Submitting this to optimise to QST2 fails as it is too far from the transition state. By changing the dihedral angle between atoms 2, 3, 4 and 5 to 0 degrees and then change the between 2,3 and 4 to 100 degrees and the same for 5, 4 and 3. Change the corresponding atoms on the product molecule as well so they look like this:

Now the job was run again and is successful.

Table 4: Data for the boat transition state from the QST2 optimisation method

Optimised TS Structure
Terminal C-C bond length/ Å	2.14
Energy/ Hartrees	-231.603
Imaginary frequency (cm-1)	-840
Animation

The imaginary frequency still shows that the bond formation and breaking is concerted.

---

Intrinisic Reaction Coordinate

It is impossible to predict which conformer will be produced by each transition state. There is a calculation called Intrinisic Reaction Coordinate (IRC) which follows the molecules structure along the energy surface. To carry out this calculation, open the .chk file of one of the chair transition states and select 'set up calculation'. Change the job type to IRC, now a different set of options will show up. Since the transition state is symmetric, we only need to compute in one direction, therefore select forward direction and 'calculate force constant' is set to once. Then we need to set how many points the set up will calculate, the default is 6, so we will run one at 50 and then one at 200. If not enough points are calculated then the end point may not be reached, so more may be needed. Here are the results of both calculations.

Table 5: IRC Data

	IRC calculation with 50 points	IRC calculation with 200 points
Energy/ Hartrees	-231.689	-231.692
Picture of final set molecule
Number of points actually calculated	27	47
IRC graphs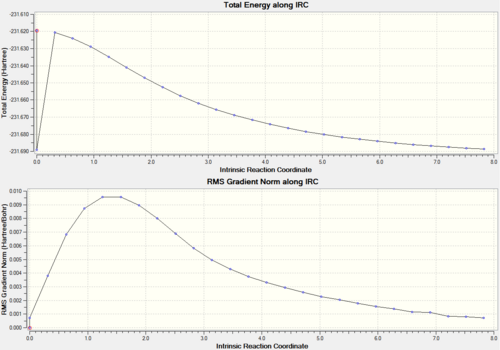

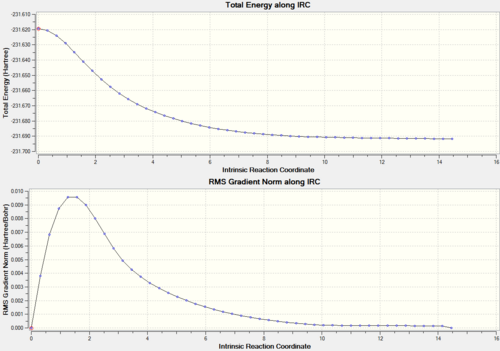
Now we can see which conformer the transition state is formed through. Even though different energies are produced, both the molecules look the same and this is the Gauche 5 conformer (from appendix). There is a bit of a hiccup in the 50 point calculation which cannot really be explained.

---

Activation Energy

To calculate the activation energy, you find the energy difference between the reactant and the transition state, but first the transition states nee dot be optimised to further using B3LYP/6-31G method starting with the HF/3-21G optimized structures.

Table 6: HF/3-21G Data of Transition states and reactant

	Energy/ Hartrees	Diagram of Molecule	File link
Chair TS	-231.619		Media:tschair_frozen_dan.LOG
Boat TS	-231.603		Media:ts_boat_dan.LOG
Reactant (Anti 2)	-231.693		Media:Ci_3-21G_dan.out

Table 7: B3LYP/6-31G Data of Transition states and reactant

	Energy/ Hartrees	Diagram of Molecule	File link
Chair TS	-234.506		Media:TSCHAIR6G31_dan.LOG
Boat TS	-234.493		Media:TSBOAT6G31_dan.LOG
Reactant (Anti 2)	-234.560		Media:Ci_6-31G_dan.LOG

Table 8: Activation Energies

	Activation Energy/ Hartrees	Activation Energy/ kcal/mol
Chair TS: HF/3-21G	0.074	46.436
Boat TS: HF/3-21G	0.090	56.476
Chair TS: B3LYP/6-31G	0.054	33.886
Boat TS: B3LYP/6-31G	0.067	42.043

The experimental activation energies for the chair transition structure is 33.5 ± 0.5 kcal/mol and 44.7 ± 2.0 kcal/mol for the boat transition structure at 0 K. The B3LYP/6-31G results are within the experimental parameters, which shows that Gaussview can be extremely accurate. The HF/3-21G is approximately 10 kcal out from the experimental but is of the same magnitude.

---

References