Rep:Mod:trm08physical

Physical Computational Chemistry

by Teddy Middlebrook

The aims of this experiment are to use a variety of different computational methods and basis sets to find a good way to characterise transition states.

Part 1 - Optimising the Reactants and Products

Hexadiene was optimised in two different conformations the results are below:

Hexadiene with anti linkage

Energy: -231.69097057

Point group: C1

This can be identified as anti4 from the table.

Hexadiene with gauche linkage

Energy: -231.69266

Point group: C1

This can be identified as gauche3 from the table.

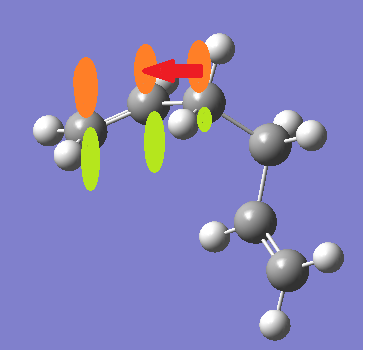
From simply looking at the molecules you would expect the anti conformation to be lower in energy that the gauche conformation because the two large groups are only 60° apart whereas in the anti conformation they are 180° apart so for steric reasons you would expect the anti conformation to be more stable. This, however, does not take electronic effects into account as electrons can be donated from the the C-H σ orbital into the C-C π* orbitals (shown below). I.e. it is a balance between the two factors which means that some gauche configurations will be lower in energy than anti configurations and some will not.

The results above show that the optimised gauche conformation found is lower in energy than the anit conformation by -4.44 kJ/mol . I will therefore draw another gauche conformation alter the geometry and optimise the structure to see if I can find a lower energy conformation. The conformation found is shown below it has an energy of -231.68961575 and has C1 symmetry (this can be identified as gauche5 from the table) and is in fact higher in energy than both the gauche and anti conformations found before. Showing that there are lots of slightly different conformations which are all minima on the reaction profile and some gauche ones are lower in energy than anti conformations and others are not.

The anti2 conformation was then drawn and optimised it has Ci symmetry and an energy of -231.69253506 which confirms that it is the anti2 conformation. The molecule was then optimised with a new method DFT, B3LYP and a 6-31G(d) basis set the resulting molecule had an almost identical geometry to the structure optimised with a more basic basis set and the calculation took at least twice as long. The energy obtained from this calculation was -234.61171054 a.u.

 Sum of electronic and zero-point Energies=           -234.469204 a.u. 
 Sum of electronic and thermal Energies=              -234.461858 a.u.
 Sum of electronic and thermal Enthalpies=            -234.460914 a.u.
 Sum of electronic and thermal Free Energies=         -234.500776 a.u.

Part 2 - Optimising the 'Boat' and 'Chair' Transition Structures

Parts a and b

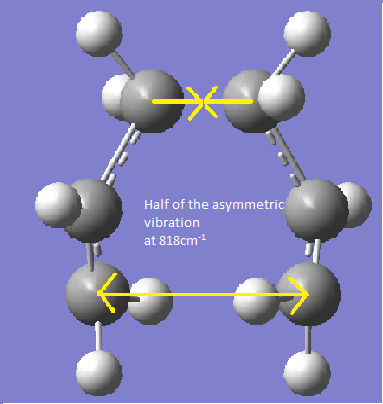
The guessed chair transition structure was made and then was optimised and a frequency calculation run using the HF 3-21G method. It gave an imaginary frequency of 818 cm^-1 which corresponds to the Cope rearrangement vibration.

Parts c and d

The frozen coordinate method was then used to optimise the guessed structure instead it looked practically identical to the transition state obtained using the previous method but the distance between the terminal C atoms lined up ready to bond were fixed at 2.2 Å. These bonds were then optimised and the bond length was reduced from 2.20 Å to 2.02 Å.

Part e

The reactant molecule anti 2 from the table was then drawn and the resulting molecule from the rearrangement also drawn, a QST2 calculation was then used in the optimisation but the job failed. The structure obtained is given here . It looks a little like the chair structure but the bonding is very strange and definitely not correct. The geometries of the molecules therefore need to be altered manually before using a QST2 calculation. The dihedral angle between the central four atoms of both the product and the reactant molecule was changed to 0 so that the starting molecules for the calculation look more like boat structures and then the optimisation was carried out. The transition structure is given here. The numbers are in the right order which confirms that the transition structure was formed.

Part f

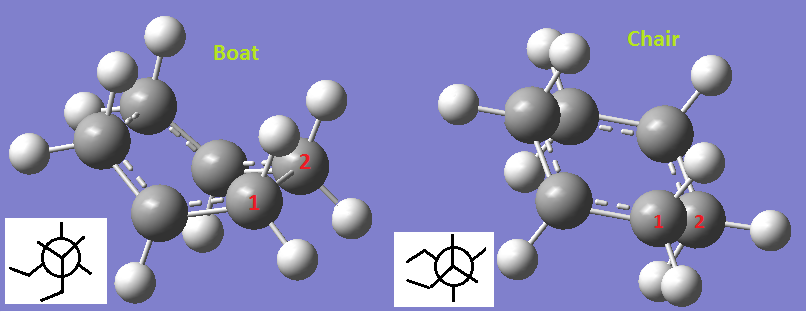
The boat structure is made up from the gauche 3 conformation and the chair conformation is formed from the gauche 1 conformation. This can be seen by looking that the central bond in the transition structures (the atoms are labelled 1 and 2). Looking down the bond between atoms one and two you can see which Newman projection for either a gauche or anti conformation is closest. The two Newman projections in the diagram below correspond to gauche 3 and gauche 1 respectively.

Part g

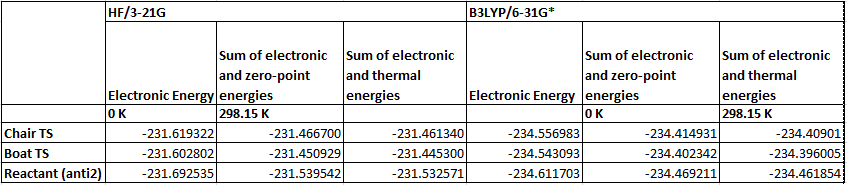
The boat structure optimised using the HF, 3-21G method gave an energy of -231.60280249 a.u. This structure was then reoptimised using the B3LYP, 6-31G* method and the energy obtained from this calculation was -234.54309295 a.u. Despite the large difference in energy the structures are practically identical. To save time on calculations it is a good idea to optimise the structure at a low level first and then to reoptimize using a higher level method and more computationally expensive method when the structure is already optimised to some degree. Both structures were reoptimised this way and frequency calculations run so that the activation energy could be determined. The energies using the different methods and the calculated activation energies for each structure are given below.

Figure 1. Table summarising the energies of the different structure (N.B. all energies are in Hartree)

Figure 2. Table showing the activation energies (N.B. all energies are given in kcal/mol)

Part 3 - The Diels-Alder Cycloaddition

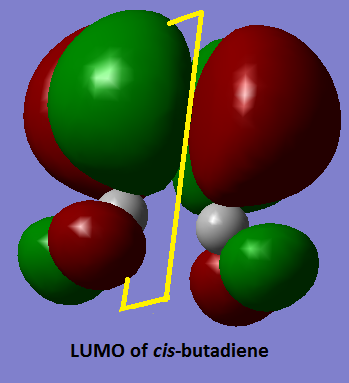
Cis-Butadiene was drawn and optimised using the HF/3-21G method. The MO’s were plotted to determine the symmetry of the HOMO and LUMO. From looking at the MO’s (pictured below) you can see that with respect to the plane of symmetry drawn on the molecule the HOMO is symmetric and the LUMO is antisymmetric.

HOMO cis-Butadiene

LUMO cis-Butadiene

Now that the starting materials have been examined the transition state of the molecule must be examined. Firstly the structure of the transition state must be guessed. Starting with a ready made bicyclo[2.2.2]octane ring a CH-CH unit was deleted, a double bond was added and two of the bonds were made into dotted lines and the distance between the atoms altered so that it was 2 Å.

The molecule was initially optimised using the AM1 method, however, the orbitals generated were extremely strange so instead the molecule was optimised using the HF/3-21G method. The molecule can be seen here.

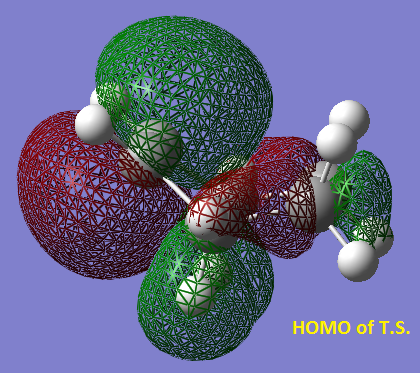
When the structure was optimised the partly formed bonds changed from 2 Å to 1.52 Å. (The rest of the bonds are between 1.33 Å and 1.52 Å. The HOMO is shown below.

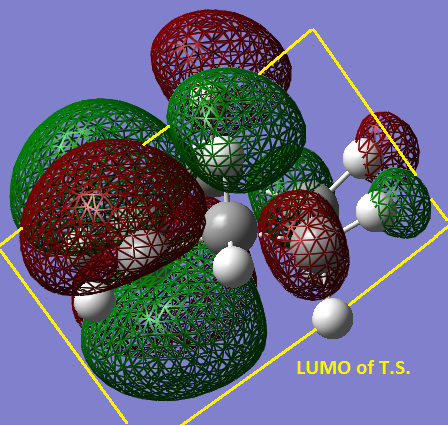
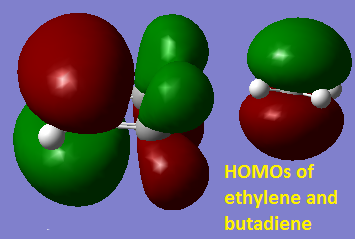
It is symmetric with respect to the plane of symmetry which is shown on the LUMO. The LUMO is antisymmetric with respect to the plane of symmetry. The MO’s of butadiene and ethylene used to form the HOMO of the transition state are the HOMOs of both separate molecules, you can see this by comparing the diagram below picturing the HOMOs of both separate molecules close together ready to form the transition state and the HOMO of the transition state given above. The reaction is allowed because they are both of the same symmetry symmetric with respect to the plane drawn previously.

The partly formed bonds are about the same length as an sp³ C-C bond. Typical sp³ bond lengths between carbon atoms are around 1.54 Å ^[1] whereas typical C-C sp² bond lengths are around 1.46 Å^[1] however if pi interactions are involved i.e. a C=C the bond length is lowered to 1.34 Å^[1]. The van der Waals radius of the C atom is 1.70 Å^[2]. The partly formed bond of length 1.52 Å is less than the sum of the two van der Waals radii which shows there is some overlap so a bond is being formed, when the length of it is compared to the other bonds a C-C is forming.

The vibration that corresponds to the reaction path at the transition state is at 848 cm^-1 the vibration is illustrated below, note that the formation of the two bonds is synchronous.

The vibration at the next lowest positive frequency of 916 cm^-1 is the same breathing stretch of the partly formed bonds but it is the asymmetric vibration.

The regioselectivity of the Diels-Alder Reaction will now be studied. The reaction scheme is given below:

The major product is the endo product. The energy of both the exo and endo transition states will be calculated to determine whether the reaction is kinetically controlled, if it is the exo transition state will be higher in energy. Firstly the two transition structures were drawn manually the partially formed bonds were set to 2 Å and the AM1 method was used (the structures were minimised to a TS(Berny), the force constant was calculated once and the keywords ‘Opt=NoEigen’). The exo transition structure has an energy of -0.050503 a.u.(this is definitely a transition structure as it has an energy of -812 cm^-1) and the endo transition structure has an energy of -0.051594 a.u. (this is definitely a transition structure as it has an energy of -805 cm^-1) this is an energy difference of 0.6 kcal/mol. The transition structure for the exo form is higher in energy which is as expected.

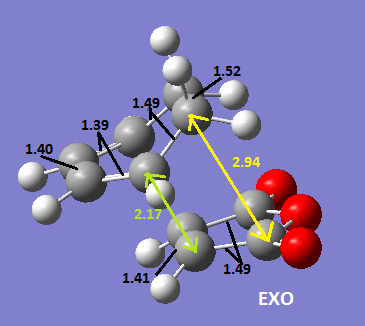
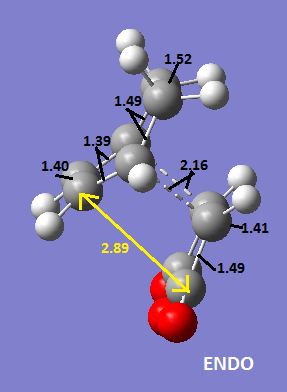
The two structures are shown below with the different C-C bond distances drawn on(all bond lengths are in Angstrom.

It shows that the partially formed bond is 2.16 Å for the endo and 2.17 Å for the exo structure i.e. there is barely any difference. However, the distance between the maleic anhydride C=O carbon atoms and the CH2CH2 fragment is 2.94 Å for the exo structure and the the distance between the maleic anhydride C=O carbon atoms and the CH=CH fragment is 2.89 Å for the endo structure. There is a balance between steric interactions and secondary orbital overlap effect; from the diagram of the HOMOs of the two structures below you can see that there are secondary orbital overlap effects for the exo structure but not the endo structure between the C=O orbitals and the CH=CH orbitals as they are in the same phase. However, there are much larger overlaps between the CH=CH of the maleic anhydride framgent and the CH₂CH₂ fragment of the diene. These interactions stabilise the transition state of the endo structure therefore it is lower in energy and will therefore be the thermodynamic product of the reaction.

The interactions between these orbitals in the exo structure has a destabilising effect because they are in a different phase, so the transition state will be more strained and therefore higher in energy.

Using semi-empirical methods e.e. AM1 can sometimes agree with predictions about stability which include orbital effects because the results use experimental data. However, this is only really true for systems in their ground state, not for transition states so it is a limitation in this case, if the orbital effects were taken into account for the transition states then I would expect the energies of the endo and exo structures to have a larger difference in energy.

References

[1] H. A. Bent, Chem. Rev., 1961, 61 (3), pp 275–311

[2] A. Bondi, J. Phys. Chem. 1964, 68 (3), pp 441–51