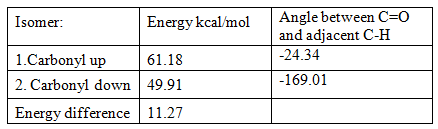Rep:Mod:trm08
Using molecular mechanics to predict geometry and regioselectivity
Introduction - What is molecular mechanics?
Molecular mechanics uses classical physics to model a molecule, it does this by calculating the potential energy using a force field. The following calculations are run using an MM2 force field. This is an empirical force field based on many approximations, however, despite its simplicity when it is used solely on hydrocarbons and their derivatives it provides useful results consistent with experimental data. It works to minimise the steric energy of the molecule by optimising the geometry. The energy calculated is shown in the following equation and takes both bonding and non bonding factors into account [1]:
E steric = E bond + E angle + E dihedral +E electrostatic + E vanderwaals
Parameters are set with this method so that for each atom the atomic mass, van der Waals radius and partial charge is taken into account and for groups of atoms the equilibrium bond lengths, angles and dihedrals are taken into account.
The energies are calculated by modelling the bonds and bond angles as harmonic oscillators, using the Lennard-Jones potential to calculate Evanderwaals and Coulomb’s Law to calculate Eelectrostatic.
There are some disadvantages with using this technique mainly that it is less accurate for molecules that contain atoms other than CHNO and that it does not take electronic effects or coupling into account. Also for many atom molecules there can be lots of minima and the geometry of a molecule may have to be altered manually to ensure that the energy is minimised to the minimum with the lowest energy rather than the minima closest to the initial geometry.
Example 1 – The Hydrogenation of a Cyclopentadiene Dimer
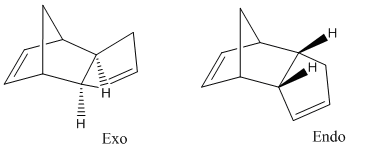
The endo form of the cyclopentadiene dimer is the preferred conformation due to the way that the two molecules approach one another in order for the Diels-Alder reaction to occur see Endo addition rule for a further explanation. Molecular mechanics can be used to investigate the relative stabilities of both the endo and exo forms to provide evidence to support the Endo addition rule. After optimising the geometry to minimise the energy the following energies were produced:
N.B. All energy values in this report have been rounded to the nearest 2 d.p.
These results indicate that the exo form is the most stable form, the energy contribution that contributes the most towards the extra thermodynamic stability of the exo form is the difference in torsional strain. This is because as you can see by rotating the pictures above the rings in the exo form adopt a more staggered conformation than in the endo form.
However, experimental evidence[2] has shown that cyclopentadiene dimerises via a stereospecific mechanism and only produces the endo conformation. This is because the reactivity of cyclodimerisation can either be controlled thermodynamically or kinetically, the results from the molecular modelling show that if the reaction was controlled thermodynamically the conformation observed would be the exo conformer, we know however that this is not the case, the observed reactivity must therefore be due to kinetic factors such as transition state stability rather than the overall stability of the product.
Reaction Profile for the Formation of the Conformers
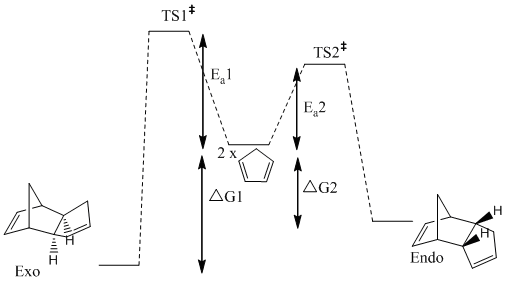
The results obtained can be explained using the reaction profile above, in order for a reaction to be controlled kinetically the activation energy of the less thermodynamically stable (endo) product must be lower than the activation energy of the more stable product, i.e. Ea1<Ea2. Formation of the higher energy product alone shows that the reaction is under kinetic control, if the exo product had been formed the reaction could either have been under thermodynamic or kinetic control.
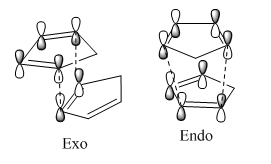
From the diagram of the two cyclopentadiene rings approaching each other to form both the endo and the exo product it is clear that the endo transition state would be much more stable due to the secondary orbital interactions between the overlapping orbitals of the top and bottom molecules that are not involved in the pericyclic reaction.
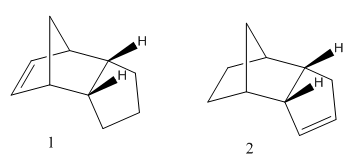
Hydrogenation of the cyclopentadiene dimer gives one of the two products shown. (The molecule becomes fully saturated after prolonged hydrogenation).
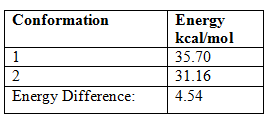
After optimising the geometry to minimise the energy of the hydrogenated products the following conformations and energies were produced:
The more thermodynamically stable product is therefore product 2.
The relative contributions to the energy from bond stretching, bending, torsion and van der Waals can be compared for the two species.
It is clear from the table above that the main difference in energy between the two possible products can be attributed to the bending energy. The product of the hydrogenation reaction is product 2 the lower bending energy means that the molecule is less strained this is because the double bond that is hydrogenated is the more strained bond, i.e. the double bond of the bicyclic ring.[3] The hydrogenation reaction is under either thermodynamic or kinetic control as the lower energy product is formed the control of this reaction could be altered for example by adding a catalyst.
Example 2 – Stereochemistry of Nucleophilic Additions to a Pyridinium Ring (NAD+ analogue)
Reaction 1
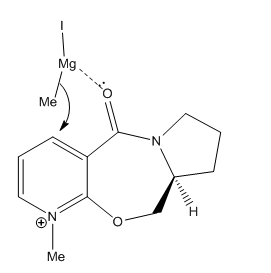
The first reaction to be investigated is a prolinol derivative reacting with MeMgI to alkylate the pyridine ring stereospecifically in the 4-position, in the following way:
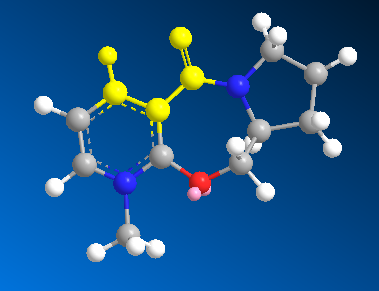
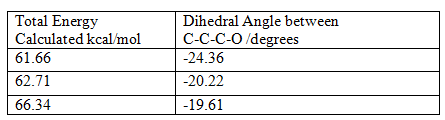
In order to rationalise the observed results it is crucial to look at the geometry of the carbonyl group with respect to the aromatic ring. The angle being calculated is shown in the diagram below:
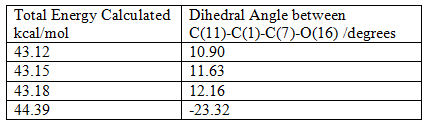
The table shows that as the angle between the carbonyl group and the aromatic ring tends towards zero the molecule becomes more stabilised. This is because when the carbonyl group is in the same plane as the aromatic group it is resonance stabilised, the oxygen lone pair has to be in the same plane as the pyridine π* orbitals i.e. the relative orientation of the interacting orbitals is important.
The value at the bottom of the table is actually due to the enantiomer of the molecule being investigated, it is of slightly higher energy.
The significance of the angle between the carbonyl group and the pyridine ring is that there are two conformational minima for the molecule; one with the carbonyl group in the same plane as the ring and the other with the carbonyl group above the plane of the ring antiperiplanar to the H atom at the chiral centre. There is, however, no conformation in which the carbonyl group is below the plane, synperiplanar to the H atom on the chiral carbon. This is the origin of the stereochemistry, it can be shown by looking at the start of the mechanism.
The MeMgI (Grignard reagent) firstly coordinates to the carbonyl group, the Me group then acts as a nucleophile and attacks the electrophilic carbon at the 4-position (it attacks at the 4-position because the positive charge on N can be exacerbated onto that position, this can be shown by drawing resonance forms of the pyridinium ion). The two possible ways it could attack are above the plane or below the plane, however, because the carbonyl group can only be in the plane of the ring or slightly above the coordinated nucleophile can only attack from above the plane, leading to a single isomer.
The carbonyl group cannot be below the plane because the stabilisation gained from the interaction of the oxygen lone pair and the pyridine π* orbitals would be lost.
If you put the MeMgI component into the calculation an error message come up which says “WARNING! No atom type was assigned to the selected atom!” this is because the MM2 force-field calculations are primarily for organic molecules and their derivatives where there is a lot of experimental evidence. Putting a more unusual atom such as Mg is likely to return very bad results as there is not enough data to support a model with Mg in it if you just use MM2 with it's fixed parameters, however you can change MM2 manually so that other atoms can be included.
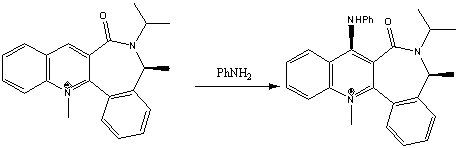
Reaction 2
This reaction involves the addition of –NHPh to a pyridine based ring system. Like the reaction above the –NHPh is added stereospecifically above the plane of the ring. See the reaction scheme below:
The angle between the carbonyl group and the pyridine ring has been calculated for slightly different conformations, the results are below.
The most thermodynamically stable optimised conformation has the carbonyl group below the plane of the molecule by a slightly larger angle. It is the fact that the carbonyl group is fixed out of the plane of the molecule that leads to the stereocontrol when –NHPh is added to the molecule because the nucleophile has to attack above the plane of the molecule to minimise steric hindrance so the bond forms above the plane of the molecule.
These simple models could be improved by taking other molecular interactions and stabilising features into account such as aromaticity, orbital and electronic effects.
Example 3 - Stereochemistry and Reactivity of an Intermediate in the synthesis of Taxol
A key intermediate in the synthesis of Taxol has some interesting chemistry; it exists as two isomers which if left to stand both isomerise to the other isomer. They are shown below:
The difference between these isomers is that the carbonyl group either points up or down. After running an MM2 force-field calculation the geometries of these isomers can be optimised, edited manually and their minimum energies calculated to determine the most stable isomer, the results are below:
The angle measured is highlighted in the structure below:
These are examples of atropisomers. The difference in their thermodynamic stability is due to the dihedral angle between the carbonyl group and the hydrogen on the adjacent carbon atom. When the carbonyl group is pointing down the hydrogen is staggered but when carbonyl is pointing upwards the hydrogen is almost eclipsed, destabilising that conformation. The alkene functional group in this molecule reacts extremely slowly because it is a ‘hyperstable’ olefin and is less strained than the parent hydrocarbon because the double bond is located at the bridgehead of the molecule. [4] It is an example of the limitations of Bredt’s Rule and can be described as an ‘anti-Bredt olefin’ if you remove the double bond from the optimised configuration and calculate the energy for the hydrogenated product it is 72.97 kcal/mol which is 23.06 kcal/mol higher in energy than the most stable atropisomer which is a significant amount.
If the MMFF94 field is used the energies of the two atropisomers are as follows:
The absolute energies obtained by the two different forcefields cannot be compared, however, the energy differences between the isomers are significantly different.
Modelling Using Semi-empirical Molecular Orbital Theory
The purpose of this approach is to improve the purely mechanical method by including electronic interactions and how they affect the reactivity of various molecules i.e. by using a quantum mechanical approach.
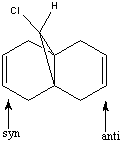
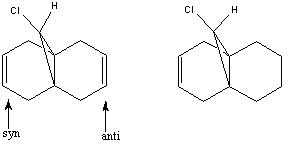
Example 4 – Regioselective Addition of Dichlorocarbene[5]
After minimising the energy using MM2 the following conformation is given:
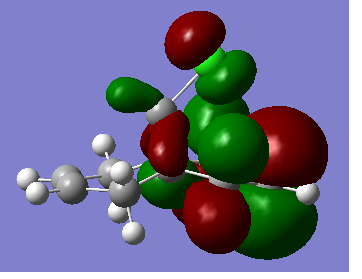
Which has an energy of 17.91 kcal/mol. MOPAC/PM 6 was then used on the conformation to give the HOMO which is shown below.
It is clear from this diagram that the alkene functionality on the same side of the molecule as the chlorine atom (the syn alkene) will be the most reactive towards electrophilic attack because the HOMO acts as a nucleophile and all of the electron density of the HOMO is centred on the syn C=C bond.
The other molecular orbitals can be calculated and are shown below.
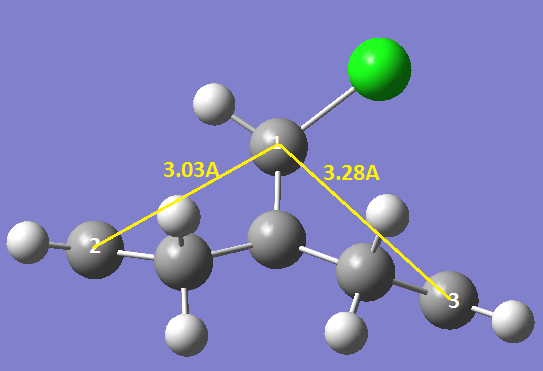
From these MO’s you can see that if the HOMO-1 was superimposed onto the LUMO+2 there would be significant overlap between the πC=C orbital of the anti alkene and the σ*C-Cl orbital, this is indeed the case and is further supported by close inspection of the molecule. The anti double bond is tilted upwards slightly towards the C-Cl whereas the syn bond is not this is shown in the diagram below:
A quantitative measure of this tilting can be given by calculating the distance between the central carbon atom and the double bond, which shows that the distance between the anti double bond and the main carbon is shorter. Another way to show these effects is to look at the IR spectra of the molecules.
Calculating the influence of the Cl-C bond on the vibrational frequencies of the molecule
In order to do this two molecules will be compared, the molecule above and a derivative of this molecule formed when the double bond anti to the Cl molecule is hydrogenated. The two molecules are shown below.
The energies calculated using the MM2 force field are 17.91 kcal/mol and 24.82 kcal/mol respectively. The sum of the electronic and energies calculated using Gaussian are -888.18 Hartree and -886.98 Hartree respectively.
The geometries of these molecules were optimised and their energies calculated using both the MM2 force field and Mopac, then the IR stretching frequencies were calculated using Gaussian, the spectra of the molecules are shown below.
Looking at the vibrational frequencies of the two molecules there is a shift in the vibrational frequency of the C-Cl stretch going from the original to the hydrogenated product, it has a higher wavenumber and therefore has a higher corresponding wavelength so the stretch is of lower energy in compound 2. This means that the C-Cl bond in the hydrogenated molecule is stronger than in compound 1. A possible explanation for this is that there is donation from the exo alkene’s πC=C orbital into the antibonding σ*C-Cl orbital, donation into antibonding orbitals decreases the strength of the C-Cl bond.
The IR spectra also show two C=C stretches at around 1700cm-1 for the original compound and only one for the hydrogenated molecule as expected.
The two stretches at 3102.67 cm-1 and 3144.15 cm-1 due to extra stretches that are present in the hydrogenated derivative but not the original molecule support the orbital explanation above because if there is donation from the πC=C into the σ*C-Cl the flexibility and possible stretches of the cyclopropane-like ring in the molecule will be restricted.
References
[1] E. Osawa, H. Musso, Angew. Chern. Inf. Ed. Engl., 1983, 22, pp1-12
[2] N. J. Turro, G. S. Hammond, J. Am. Chem. Soc., 1962, 84 (14), pp 2841–2842
[3] T. J. Katz, M. Rosenberger, R. K. O'Hara, J. Am. Chem. Soc., 1964, 86, 2, pp 249–252
[4] W. F. Maier and P. von Ragu, C. Schleyer, J. Am. Chem. Soc., 1981, 103, 8
[5] B. Halton, R. Boese and H. S. Rzepa., J. Chem. Soc., Perkin Trans 2, 1992, 447. DOI:10.1039/P29920000447
Part 2 - Structure based Mini project using DFT-based Molecular orbital methods
I am going to investigate the selectivity of the following reaction:
This reaction was found in an article partly researched at Imperial College in 2004 entitled ‘Reagent-Controlled Stereoselective Synthesis of Lignan-Related Tetrahydrofurans’[1]. I am going to use R=MeO-Ph, there were 23 R-groups listed all with 13C NMR data and ratios of the isomers. I have chosen this R group because it is the one with the largest difference between chemical shifts for the same peaks. The root mean square error due to the computational calculations used is 2 ppm therefore I was looking for the molecule with an R group that had shifts in the 13C NMR peaks which were greater than 5 ppm.
The journal gives the ratio of isomers A:B as 8:92. In order to calculate this the researchers must have found a way to differentiate spectroscopically between the isomeric products. The key methods used to distinguish between isomers like these are optical rotation measurements, analysing the NMR spectra,
In the literature NOE was used extensively, this looks at the relative distances between different atoms through space unlike NMR which looks at the distances through bonds.
To start with the geometries of isomers A and B were optimised Molecule A Energies: Stretch: 2.00
Bend: 8.87
Stretch-Bend: 0.25
Torsion: -4.41
Non-1,4 VDW: -3.14
1,4 VDW: 24.16
Dipole/Dipole: 1.07
Total Energy: 28.80 kcal/mol
Molecule B Energies:
Stretch: 1.86
Bend: 8.28
Stretch-Bend: 0.25
Torsion: -3.67
Non-1,4 VDW: -4.22
1,4 VDW: 23.76
Dipole/Dipole: 0.48
Total Energy: 26.74 kcal/mol
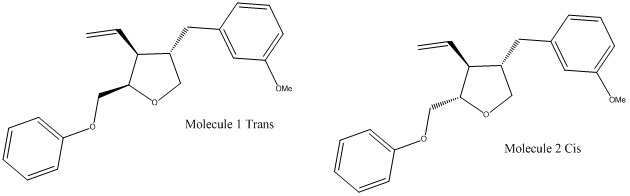
The isomers are different in energy the the trans form is more stabilised than the cis form which is unusual as the two large aryl groups are on the same side, this is likely to be because when the two largest aryl groups are cis the alkene group between the groups is on the other side of the molecule, however, in the trans form both the alkene group and a neighbouring aryl group are on the same side. The literature states, however, that the ratio of products is trans:cis 8:92 therefore the reaction must be kinetically controlled and therefore depends on the mechanism and energy of the transition state. However, before the mechanism is inspected closely the geometry will be minimized further at the Gaussian mpw1pw91/6-31(d,p) level. The output of this method was inspected to check that the geometry of the molecule was still reasonable before proceeding.
The NMR Shift calculation was then run with the newly optimised molecule, the literature reported that the 13NMR was done in CDCl3 at 75MHz so the reference for the calculation was also CDCl3.
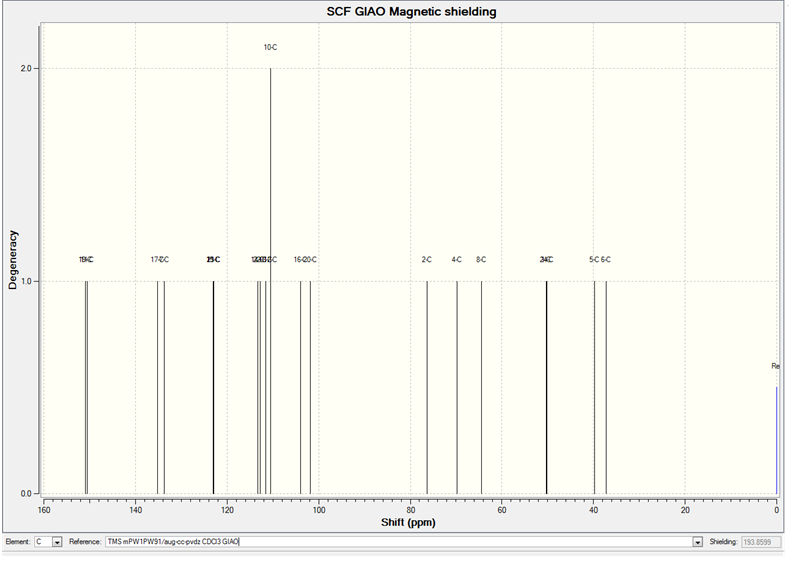
Once optimised basically using MM2 the optimised geometries were submitted to SCAN and minimised further using Gaussian once this was done the 13C NMR spectra were predicted for the isomers using the GIAO method.
The calculated 13C NMR Spectrum for the trans product is shown below:
The calculated 13C NMR for the cis product is shown below:
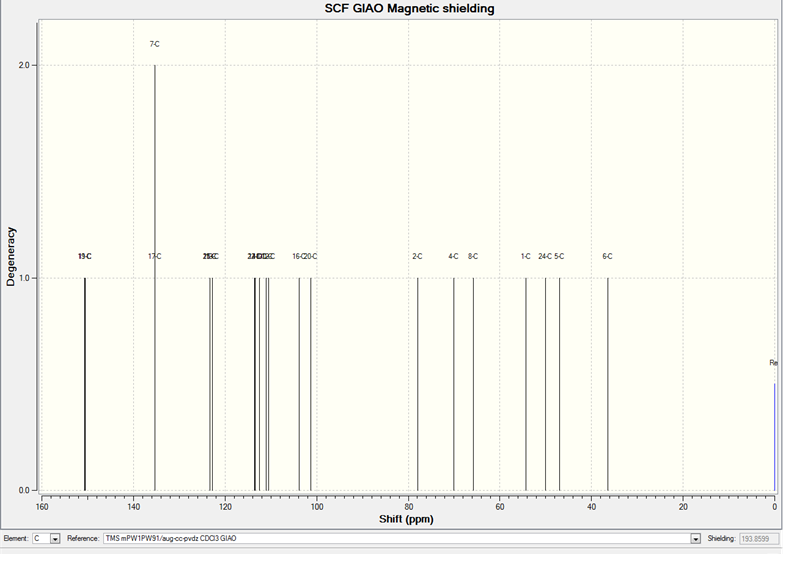
The full sets of data for the trans and cis products are given here: Trans DOI:10042/to-5690 Cis DOI:10042/to-5691
The shifts for the two isomers from the literature are:
13C NMR (signals for cis, 75 MHz, CDCl3) δ 38.0 (t), 47.7 (d), 55.2 (q), 55.3 (q), 59.5 (d), 73.3 (t), 85.6 (d), 111.4 (d), 113.3 (d), 113.7 (d), 118.0 (t), 121.1 (d), 127.3 (d), 129.5 (d), 133.5 (s), 136.7 (d), 141.9 (s), 159.1 (s), 159.7 (s); signals for minor isomer 8p trans visible at δ 37.5 (t), 55.1 (d), 83.2 (d).
The peak that I am going to use to differentiate between the two isomers is the peak at 59.5 ppm (d) for the cis molecule that shifts to 55.1 ppm (d) for the trans molecule. The calculations are only accurate to about 2 ppm, however, there is still a clear shift in the peak due to 1C from 54.4 (for the cis isomer) to 50.3 ppm (for the trans isomer). There is another clear shift in the literature values from 85.6 ppm (cis) to 83.2 ppm (trans). These shifts can be seen in the calculated values:
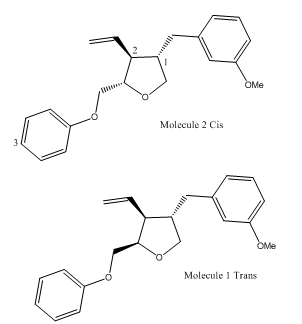
From this it is clear that there are four main differences in between the chemical shifts of the isomers. These can be assigned to different atoms labelled 1-3 on the following diagram.
Atoms 1 and 2 in the trans molecule are more shielded than in the cis, whereas atom 3 in the trans molecule is less shielded than in the cis.
The shift given in the literature from 38.0 ppm to 37.5 ppm cannot be seen in the calculated values because it is too small, there is a change but it is an increase in the shift rather than a decrease, this is just likely to be due to the approximations made and the exact configuration of the molecule used rather than an actual change in chemical shift.
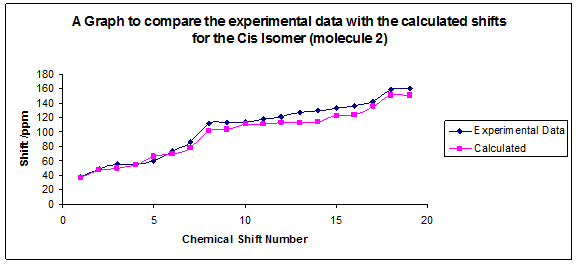
A graph has been plotted to show how close the calculated results are to the literature values:
From this you can see that despite the approximations made the results agree with the experimentally determined ones very closely, the method should therefore be used more often in organic chemistry with molecules of this sort to predict NMR spectra. The results also agree with the way that the isomers have been assigned in the paper, the cis results correspond correctly to the optimised cis structure.
1H NMR is inaccurate when calculated, the shifts are quite far out but the coupling constants can be used as they only depend on the differences between chemical shifts, not the shifts themselves. The coupling constants were calculated, for the cis molecule they were JHa-Hc = 10.67, JHb-Hc = 5.16, JHe-Hd = 6.27 and for the trans molecule they were JHa-Hc = 9.21, JHb-Hc = 1.79, JHe-Hd = 4.20 there is a difference between these coupling constants which were chosen to be calculated as they have positions that change the most between the isomers (the atoms are shown on the diagram below of the cis isomer). The calculated values do not closely correspond to the values in the literature, in general though the coupling constants for the cis molecule in both the literature and the calculations are higher than those of the trans. The literature constants are not assigned so it is difficult to see exactly which pairs of atoms they correspond to.
The mechanism is given below, this might help to explain the stereoselectivity.
Miles et al. rationalised the stereoselectivity of the reaction with the mechanism above, they decided (without the aid of computational chemistry which would have helped them to confirm that the less stable product is the trans isomer) that the kinetic product of the reaction was the trans isomer and under certain reaction conditions with electron rich substituents on the aldehyde and a Lewis acid present the trans isomer would be formed via a reversible ring opening of the cis product to a ‘stabilised benzylic cation’. [2]
References
[1] S.M. Miles, S.P. Marsden, R.J. Leatherbarrow, J.Org. Chem., 2004, 69, pp 6874-6882
[2] Y. Jiang, J. Stivers, Tetrahedron Lett., 2003, 44, pp85-88