Rep:Mod:transstates mkn112

All the .log files can be found on this page.

The main objective of the experiment is the analysis of the transition states and reaction pathways of various molecules using molecular modelling with Gaussian. One of the problems that experimental chemistry faces is the very short lifetime of transition states, which hinders their physical analysis and, therefore, the study of reaction mechanisms. Moreover, it is impossible to obtain total energies of the molecules, only energy differences. In the quantum chemical calculations of the total energies of molecular orbitals, Schrödinger equation is used in order to make some predictions about reaction pathways, transition states and intermediates.

The algorithm that Gaussian operates on starts with setting the atoms infinitely apart and setting the energy to 0. Then, as the atoms approach each other and electron-nucleus attraction occurs, it calculates corresponding stabilising negative energies of the system. The result of the computation is a potential energy surface (PES) which can be described as a function of geometry vs. energy. Although it is a multidimensional structure (3N-6 where N is the number of degrees of freedom), it is often represented as a 3-dimensional plot comprising of valleys (minima corresponding to stable conformations) and peaks (maxima corresponding to transition states).

In this experiment, two approaches were taken towards calculating the energies of the molecules, i.e. HF (Hartree-Fock) and DFT (Density Functional Theory). They are both used to describe the quantum states of many electron systems using Born-Oppenheimer approximation. However, HF assumes that many electron system can be described using a single Slater determinant, which results in neglecting the electron interactions. DFT, on the other hand, deals mostly with the electron densities, which allows it to take electron correlation into account. Moreover, two different basis sets were used, i.e. 3-21G for HF and 6-31G for DFT. They are split-valence basis sets (SV) that describe valence AO with two basis functions and inner shell AO with one basis function. It results in a good compromise between the accuracy and the efficiency of the computations.

Nf710 (talk) 17:20, 3 December 2015 (UTC) Very ncie intro. good basic knowledge of HF and DFT. you are correct HF cannot correlate between electrons of different spin in the same spacial orbital, this is wrong and there it gets their repulsion wrong

Tutorial: The Cope Rearrangement

Cope rearrangement

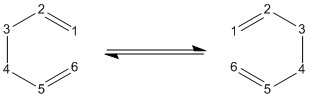
Cope rearrangement is a pericyclic [3,3]-sigmatropic reaction that involves rearranging a 1,5-diene into one of its structural isomers . It is considered to be a concerted reaction (where bonds are formed and broken at the same time), which is justified by the computational analysis. The rearrangement of 1,5-hexadiene was chosen as an example of the cope reaction. Since the molecule is free to rotate along the single bonds, there are numerous conformations it can take. Various 1,5-hexadiene conformers were optimized using two levels of theory (HF/3-21G and DFT/6-31G) to find the lowest energy one. In order to prove the concerted nature of the reaction, the possible transition states (boat and chair structures) were also optimized and analysed.

Optimizing the reactants and products

antiperiplanar conformation	synperiplanar (gauche) conformation

In order to find the lowest energy reactants and products various guess structures of 1,5-hexadiene were drawn using GaussView and then optimised with Gaussian. The starting point for the analysis were antiperiplanar and synperiplanar conformers that can be interchanged by the rotation about C3-C4 single bond.

1,5-hexadiene antiperiplanar conformer

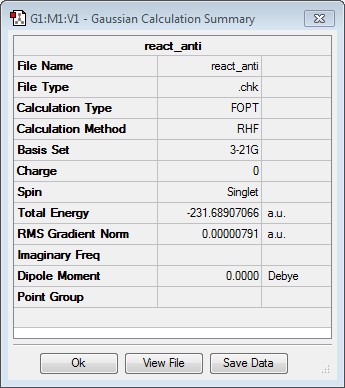
GaussView was used to draw 1,5-hexadiene with an anti-linkage, i.e. with the dihedral angle equal to 180°. Once the structure was cleaned and symmetrised, it was optimiesd using the HF level of theory and 3-21G basis set. The energy of the molecule was found to be -231.68907066 a.u. and the resulting point group was C2h, which correspond to the structure anti3. The structure of the molecule and the results summary are shown below.

antiperiplanar 1,5-hexadiene	results summary
HF/3-21G optimised anti3

1,5-hexadiene gauche conformer

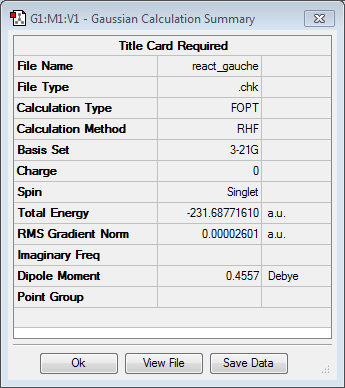
Gauche conformer of 1,5-hexadiene was drawn in GaussView and also optimised using the Hartee Fock method and 3-21G basis set. The point group of the molecule was found to be C2 and its energy was -231.68771610 a.u. The energy of this particular conformer proves to be very similar but slightly higher than the energy of the antiperiplanar conformer calculated above. It may be caused by significant steric effects that are present at the end groups of the molecule.

synperiplanar 1,5-hexadiene	results summary
HF/3-21G optimised gauche

Lowest energy conformer

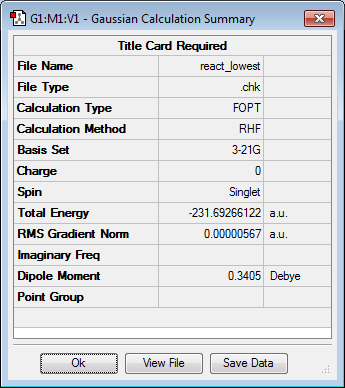
However, the potential energy surface of 1,5-hexadiene has more than two minima. In order to investigate its structure various other possible conformations of 1,5-hexadiene were constructed and optimised using the same level of theory as previously. The molecule below represents the lowest energy conformer found (gauche3), with the energy of -231.69266122 and C1 point group.

lowest energy 1,5-hexadiene	results summary
HF/3-21G optimised gauche3

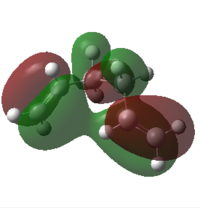
Intuitively, the lowest energy 1,5-hexadiene would probably be one of the antiperiplanar conformations. In fact, their energies are very similar to the gauche3 conformation, which can be seen by comparison with the molecule in the next section. The low energy of antiperiplanar conformers is caused by minimisation of the steric hindrance within the molecule and, therefore, minimisation of the electronic repulsion. The quite surprising result of one of the gauche conformations having the lowest energy might be explained using orbital approach. It can b reasoned with stereoelectronics: there is a favourable orbital overlap between the two π orbitals from the terminal C-C double bonds, which can be seen in the picture on the right representing the HOMO orbital of the molecule.

Nf710 (talk) 17:30, 3 December 2015 (UTC) Very nice use of orbitals to show why the gauche is lower in energy

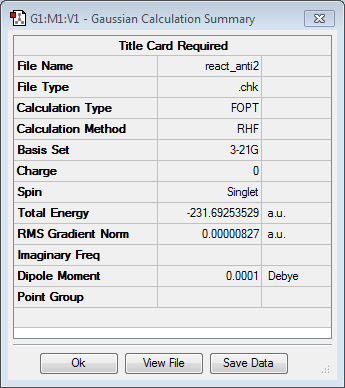
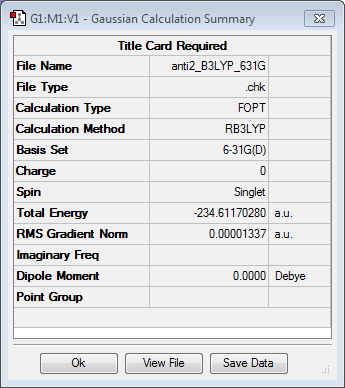
Anti2 conformer and its re-optimisation

The guess structure of anti2 was constructed and optimised using Hartee Fock method and 3-21G level of theory. The energy found was -231.69253529 a.u. and the point group was Ci. After that, the molecule was re-optimised with a higher level of theory, i.e. Density Function Theory (DFT) method and 6-31G basis set. The resulting energy of the molecule was found to be -234.61170280 a.u. and the resulting point group was Ci.

antiperiplanar 1,5-hexadiene	results summary
HF/3-21G optimised anti2
DFT/6-31G optimised anti2

At a first sight, the structures look indistinguishable, which is in fact very close to the truth. Nevertheless, there are some slight differences, both in the C-C bond lengths and the angles between the carbon atoms. Only half of the bond lengths and angles were included, since the changes were identical on both sides of the centre of the inversion. The molecule optimised using DFT/6-31G level of theory seems to be more diffuse, i.e. has slightly larger angles and longer double bonds. The rather small differences in the results prove that the found molecules correspond to the same point on the potential energy surface. Moreover, since the approximations used to calculate the energy of the molecules are different, their absolute values cannot be compared.

	Bond lengths			Bond angles
	C1-C2	C2-C3	C3-C4	C1-C2-C3	C2-C3-C4	C1-C2-C3-C4	C2-C3-C4-C5
HF/3-21G	1.316 Å	1.509 Å	1.553 Å	124.8°	111.3°	114.7°	180.0°
DFT/6-21G	1.334 Å	1.504 Å	1.548 Å	125.3°	112.7°	118.5°	180.0°

Nf710 (talk) 17:36, 3 December 2015 (UTC) Very nice clear and concise comparison of geoms. your energies are also correct

Frequency at 298K

Frequency calculation at DFT/6-31G level of theory was run. From the results file the following data was obtained:

• The sum of electronic and zero-point energies: -234.469204 a.u.
• The sum of electronic and thermal energies: -234.461857 a.u.
• The sum of electronic and thermal enthalpies: -234.460913 a.u.
• The sum of electronic and thermal free energies: -234.500778 a.u.

The first value is the potential energy at 0K including the zero-point vibrational energy correction. The second value represents the energy of the molecule at 298.15K, which includes contributions of vibrational, rotational and translational energies at that temperature. The third value involves an additional correction for RT, i.e. H=E+RT, which assumes the ideal gas behaviour of the molecule. Finally, the last value takes into account the entropy of the molecule by using thermal correction to Gibbs Free Energy. It also includes ΔNRT~ΔPV, which means that the number of moles of the gas should change with the reaction progression.

Optimising the "boat" and the "chair" transition structures

In order for the cope rearrangement to be concerted the reaction has to go through a cyclic transition state in which one sigma bond is being broken and another one is being formed. In this experiment, two of the possible conformations of the transition state were considered, i.e. the boat conformation and the chair conformation. They were optimised using various methods to analyse their benefits and their drawbacks. Moreover, the Intrinsic Reaction Pathway was found to visualise the reaction and to find the activation energies for the Cope rearrangement via the two different transition states.

A guess chair transition state was constructed in GaussView by pasting two HF/3-21G optimised allyl fragments orientated in a way they resembled a chair structure. Subsequently, the point group of the molecule was relaxed and it was symmetrised in order to set the distances between the end groups of the two fragments to 2.2 Å. This structure was then optimised using various methods.

Chair optimisation by computing the force constant at the beginning of the calculation

The guess chair structure was taken as the starting point for this optimisation. An optimisation + frequency calculation was run using the HF/3-21G method witht the TS(Berny) option chosen. Moreover, the force constant was also calculated and an additional keyword 'opt=noeigen' was included in order to prevent the program from crashing in case of more than one negative frequencies being detected.

Chair transition structure	Negative frequency motion
HF/3-21G optimised chair

The energy of the molecule was discovered to be -231.61932208 (the results summary can be seen here). As it can be seen in the table above there was one negative frequency present at -817.78 cm^-2, which corresponds to the vibration leading to Cope rearrangement. As it was previously mentioned, a transition state corresponds to saddle points on PES, which, similarly to minima, are stationary points with force constant equal to zero. However, unlike for the minima points, the second derivative of PES at a saddle point is negative due to decreasing curvature in all directions, which is represented by negative frequencies for the transition states.

Nf710 (talk) 18:01, 3 December 2015 (UTC) Not quite right the force constant is the second derivative and this is what is used in the quantum harmonic oscillator where it is sqaured rooted to get the frequency.

Chair optimisation using redundant coordinate editor

Again, the guess chair transition state was taken as the starting point for the optimisation. The distances between the terminal carbons of the two allyl fragments were set to be unchangeable using the redundant coordinate editor. An optimisation to minimum was run using the standard HF/3-21G with additional 'opt=modredundant' keyword in the input line. After the optimisation of the molecule was finished, the .chk file was open and the redundant coordinate editor was opened again. The previously frozen bonds were set to 'Derivative' and the molecule was re-optimised to TS (Berny). Using this method, the force constant was calculated only for the bond formation/breaking instead of the whole molecule.

The result was visually very similar to the previous optimisation. The energy of this molecule was found to be -231.61932233 a.u. (the results summary can be seen here). The imaginary frequency was also present at -817.88 cm^-2 which, together with its visualization, prove that the obtained molecule is a transition state.

In this case, comparison of the energies of the two molecules that were optimised using two different methods was possible, because the method and the basis set used was the same. The energy difference between the two molecules was calculated to be 0.66 Jmol^-1, which is virtually negligible. Moreover, the bond distances between the allyl groups, as well as within, were equal to 2 d.p. measured in Angstroms. In conclusion, the similarity of the structures suggests that the initial guess structure of the molecule was reasonably near the reality and, hence, the first optimisation method used resulted in a desired transition state conformation.

Boat optimisation using QST2 and QST3

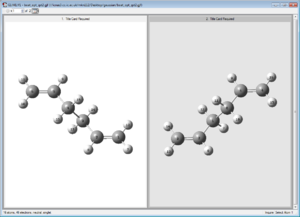
The QST2 and QST3 methods were used to optimise the boat transition state structure. Both of the methods require the reactant and the product structures, as well as labelling of the atoms corresponding to the proposed reaction mechanism. The difference between them is that QST3 also needs the guess structure of the transition state in order to perform the calculations. The first computation showed below was a QST2 method that used the antiperiplanar conformations of the starting material and the product (anti2). The obtained molecule was different from expected, since the resulting transition state is closer in structure to a chair conformation than to a boat conformation. It is caused by the program's failure to take bond rotation into account; the program simply translated one double bond above the other. Moreover, the structure is more dissociated, which can be seen by checking the bond length along the bond forming/breaking line, i.e. 3.14672 Å.

Structures of the product and the reactant	Resulting transition state
	HF/3-21G QST2 optimised boat

In order to obtain more trustworthy results, the reactants and the products were orientated in a way that resembles the actual reaction geometry more closely. The central dihedral angle on the reactant molecule was set to 0° and the inside angles (C2-C3-C4 and C3-C4-C5) were set to 100°. The product molecule was modified correspondingly. The result of this optimization is a transition structure with an energy of -231.60280239 a.u. confirmed by imaginary frequency at -839.93 cm^-2.

Structures of the product and the reactant	Resulting transition state
	HF/3-21G QST2 optimised boat

In addition to the QST2 measurements, a QST3 calculation was run on antiperiplanar product and reactant molecules with a guess transition structure provided as well. It turned out that the information provided was not enough to generate a correct transition state due to a significant difference between the initial and the final structures. A calculation involving differently aligned reactant and product molecules was not run since, taking into account that QST2 provided a satisfactory result, it would be inefficient.

Structures of the product, reactant and guessed TS	Resulting transition state

Looking at the two transition states (boat and chair) it is impossible to determine via which one the reaction would preferably proceed. Therefore, an additional Intrinsic Reaction Pathway (IRC) calculation is ought to be run in order to trace the reaction's potential energy surface from the transition structure down to its minimum point.

Nf710 (talk) 18:49, 3 December 2015 (UTC) all your frequencies are correct and this is excellently laid out.

Intrinsic Reaction Coordinate (IRC) calculation

In order to determine which transition state the reaction is going through, an IRC calculation was run. This method follows the minimum energy path from the transition structure down the steepest gradient towards its local minimum. The path is obtained by creating multiple points by slightly changing the coordinates of the atoms.

For the following calculations, an already optimised transition state structure was used. The IRC was set to be a 50 step computation and the force constant was chosen to be calculated at every step and the standard HF/3-21G method was implemented. Since cope rearrangement is a symmetrical reaction (the product and the reactant are identical), the computation was done only in the forward direction.

Cope rearrangement from the transition state	IRC plot

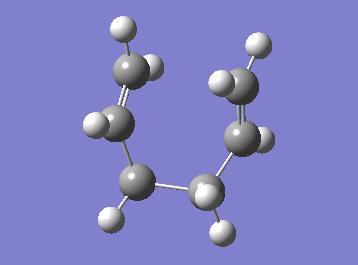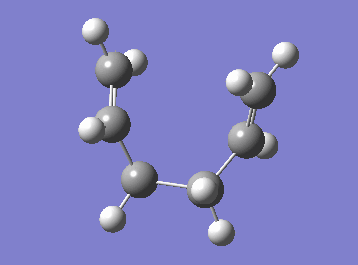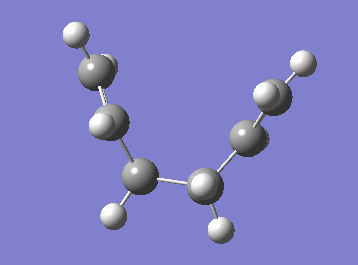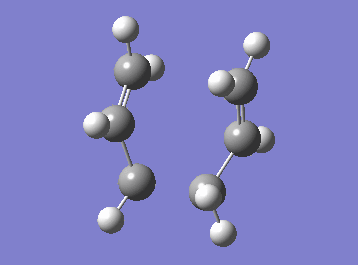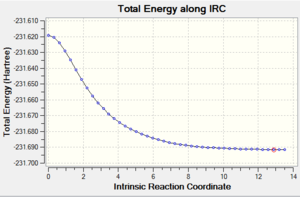The IRC plot shows the energy profile of the reaction from the transition state to either a product or a reactant. The IRC calculation stopped at the 44^th step suggesting that the minimum was found at that point, since the graph also seemed to reached the plateau. The energy was found to be -231.69157881 a.u. Two different approaches were taken in order to confirm the minimum. The first one was to run a normal optimization on the resulting molecule. The energy obtained was -231.69166702 a.u. (corresponding to the lowest energy product structure found earlier, i.e. gauche2) and the absence of imaginary frequency confirmed minimum. The second approach was to run a 70-step IRC calculation in case that the plateau lies at a lower energy. When the IRC was recalculated for 70 steps the computation stopped at the same point with the same energy value. It can be concluded that, in this particular example, an additional optimisation was not necessary to obtain the correct minimum structure.

Nf710 (talk) 12:33, 4 December 2015 (UTC) This is excellent well done. really well illustraed

The activation energies of the structures

Before the activation energies of the boat and chair transition states were compared, they were re-optimised at a higher level of theory, i.e. DFT/6-31G. When compared to the molecules optimised using HF/3-21G method, the geometry proved to be quite similar. The resulting symmetries were C2h point group for the chair TS and C2v point group for boat TS for both levels of theory. The bond distances differ only slightly, which is noted in the table below, where C1-C1 corresponds to the distance between the end carbon atoms between the two allyl fragments and C1-C2 corresponds to the distance between two adjacent carbon atoms on one allyl fragment.

	chair (Å)		boat (Å)
	C1-C1	C1-C2	C1-C1	C1-C2
HF/3-21G	2.021	1.390	2.140	1.381
B3LYP/6-31G	1.968	1.408	2.207	1.393

	HF/3-21G			DFT/6-31G
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
Chair transition state	-231.61932233	-231.466705	-231.461345	-234.55698303	-234.414929	-234.409008
Boat transition state	-231.60280239	-231.450922	-231.445294	-234.54309307	-234.402342	-234.396007
anti2	-231.69253529	-231.539540	-231.532566	-234.61171021	-234.469204	-231.461857

Since the geometries of the molecules were practically the same regardless the method used, the activation energies were also analysed in order to determine the method that delivers results closer to the experimental values. To calculate the activation energy, the difference in relative energies between the reactants and the transition states was obtained and converted into kJmol^-1 1 a.u.mol-1 = 2625.4 kJmol-1). For the activation energy at 0 K, the sums of electronic and zero-point energies were used because they involve the vibrational and rotational energies that are also present at 0 K. For the calculation of the activation energy at room temperature, the sums of electronic and thermal energies were used.

	HF.3-21G		DFT/6-31G
	0 K	298.15 K	0 K	298.15 K
Chair TS (kJmol-1)	191.22	186.98	142.49	138.75
Boat TS (kJmol-1)	232.55	229.12	175.54	172.88

From the above results it can be easily observed that the chair transition state has lower energy for both levels of theory. However, the numerical values of the activation energies are significantly different reaching up to 50 kJmol^-1. Comparing to the experimentally obtained values of activation energies at room temperature (140±2 kJmol^-1 for the chair structure and 187.1±8 for the boat structure), the DFT/6-31G proves to be more accurate, since the values are closer (the energy of the chair structure even lies within the error). It shows that for quantitative analysis of the molecular geometries both levels of theory are applicable, however, in order to calculate the energies of the molecules the slower DFT/6-31G method seems to be much more accurate.

Nf710 (talk) 18:53, 3 December 2015 (UTC) Well done! you found a reference at room temperature for the boat and chair and your have got very close to the real values. you have clearly gone beyond the script here. your electronic energies are also correct. this report is excellent written and was very pleasing to read. you backed it up with a decent understadning of the theory too. Well done.

Exercise: The Diels-Alder Cycloaddition

The Diels-Alder reaction is another example of a pericyclic concerted reaction. More specifically, it is a [4+2] cycloaddition involving an interaction of a 4π electron unit (conjugated diene) with a 2π electron unit (dienophile). The net output of the reaction is breaking two σ bonds, which makes it thermodynamically driven as σ bonds are stronger than π bonds. However, even though the reaction can proceed at room temperature, it usually requires thermal activation, which can also significantly increase the yield .

Depending on the substituents of the reactants, the Diels-Alder reaction can be either normal or inverse electron demand. Usually the main interaction occurs between the HOMO of the diene and the LUMO of the dienophile, which is considered as the normal electron demand. To facilitate the reaction, an electron donating group (EDG) can be put on the diene (to increase the energy of the HOMO level) and an electron withdrawing group (EWG) can be put on the dienophile (to decrease the energy of the LUMO level). However, in the inverse electron demand reaction the major interaction occurs between the HOMO of the dienophile and the LUMO of the diene, and, in order to facilitate the reaction, the substitution of EWG and EDG should be reversed.

In this part of the experiment, a symmetrical reaction of cis-butadiene with ethene and an unsymmetrical reaction of cyclohexa-1,3-diene with maleic anhydride will be studied. Previously described method of optimising transition states will be used to determine their symmetry and selectively. Moreover, the HOMO and LUMO orbitals will be analysed in order to show the participating interactions.

The reaction of cis-butadiene with ethene

GaussView 5.0.9 was used to construct a butadiene and an ethene molecules, which were subsequently optimised using the AM1 semi-empirical molecular method. In comparison to Hartree-Fock, semi-empirical methods are much faster due to omission or parametrisation of some of the integrals. Moreover, they are also more accurate for the molecules that are similar to the ones that are similar to the used for parametrisation .

The HOMO and LUMO of the butadiene molecule are shown below together with the Cartesian axes for reference. It can be seen that HOMO is symmetric with respect to the yz plane, while LUMO is anti-symmetric. The resulting point group of the molecule was determined to be C2v.

HOMO of butadiene	LUMO of butadiene	Cartesian axes

Optimisation of the transition state for the cis-butadiene reaction

The transition structure was generated using the optimised ethene and cis-butadiene molecules and setting them 2.2 Å apart and optimising the structure to TS (Berny) using AM1 empirical method with these coordinates frozen. Subsequently, the distance between the two molecules was unstrained in the Redundant Coordinate Editor and the molecule was optimised to TS (Berny) again. The transition state was confirmed by the presence of a negative vibrational frequency at -956.48 cm^-2 with the energy of 0.11165466 a.u. The imaginary vibrational frequency is shown below and compared to the lowest positive frequency of 147.16 cm^-2. As mentioned previously, the negative frequency corresponds to the bond formation, i.e. the reaction path at the transition state, which is in this case synchronous. On the other hand, the lowest positive frequency was found to be asynchronous rocking.

(Be careful with your units, which should be cm^-1 Tam10 (talk) 15:24, 23 November 2015 (UTC))

Negative vibrational frequency of the TS	The lowest positive vibrational frequency of the TS

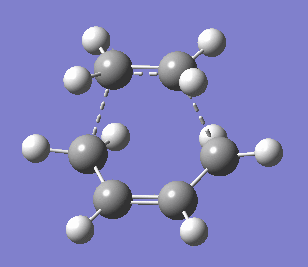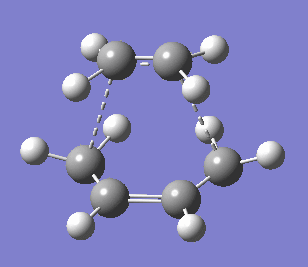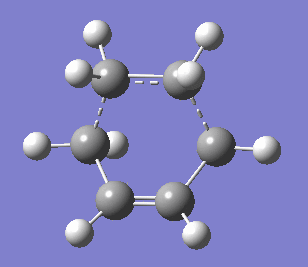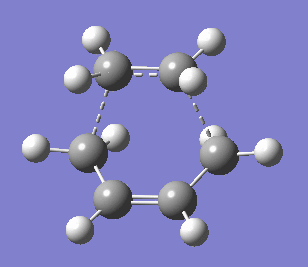IRC pathawy of the reaction

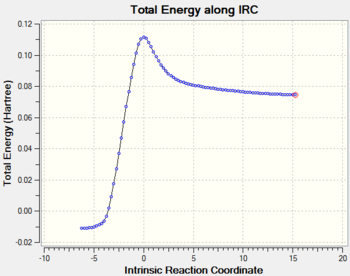
The IRC calculation was run on the transition state structure. It was found that 50 steps was not enough to reach the minimum of the reactants, therefore, the calculation was redone with 100 steps. The problem encountered with this calculation was that the IRC was calculated for the reverse reaction, i.e. starting from cyclohexene molecule and finishing with ethene and cis-butadiene. Thus, the left of the IRC plot shown below corresponds to hexane (cyclohexene Tam10 (talk) 15:24, 23 November 2015 (UTC)), whereas the right side corresponds to the reactants. Since the reaction was reversed in the calculation, also the animation was displayed as a dissociation and it had to be reversed using GIMP to get the desired forward reaction that is also shown in the table below. It can be seen in the IRC plot that the product has much lower energy It also proves that the guessed and optimised transition state connects the starting materials and the product. Furthermore, it shows that there are no intermediates and other transition states between them. If there was another transition state the IRC calculation would stop in a minimum point corresponding to the intermediate, which is not observed.

Animation of the reaction between ethene and cis-butadiene	IRC plot of the reaction

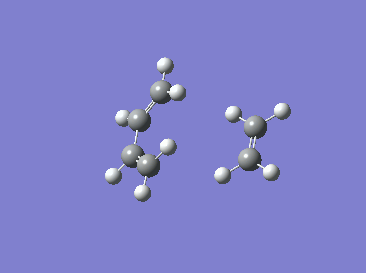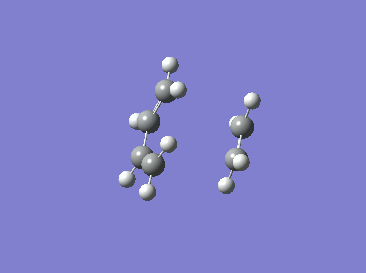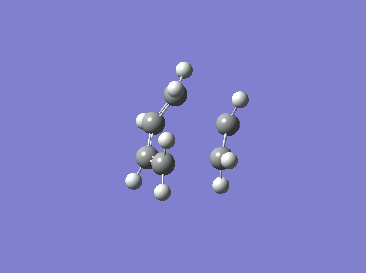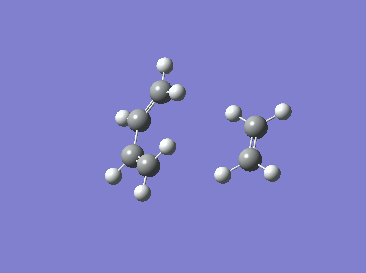The point group of the transition state for this reaction was found to be C1 and the bond length of the partly formed σ -C bonds were 2.119 Å. It is significantly larger than the bond length for sp³ and sp² hybridised carbon-carbon bonds, which are 1.54 Å and 1.34 Å, respectively However, when compared to 3.4 Å, which is double of the van der Waal radius, it proves to be much smaller. It can be concluded that a type of bonding interaction is present in the transition state, however it cannot be considered as a single bond.

The transition state for this reaction is such that it maximises the overlap of the orbitals to increase the stereoelectronic effects stabilising the molecule. It is considered to be an early transition state because its structure resembles the reactants more than the products. Similarly, it can be seen in the IRC plot that the energy of the transition state is much closer to the energy of the reactants.

MO's of ethene, cis-butadiene and the transition state

The MO's of ethene, cis-butadiene and the transition state were visualised using GaussView after running the optimizations. Additionally, the optimizations were run again in order to obtain interactive images in the jmol format, which can be seen on the separate wikipage here. The summary of the symmetries of HOMO and LUMO with respect to the plane dividing the double bond in ethene, the single bond in cis-butadiene and respectively of both in the transition state is shown in the table below together with their relative energies.

(Perhaps give a list of links at the top of the page. They can be easily missed when buried in the paragraph Tam10 (talk) 15:24, 23 November 2015 (UTC))

	Ethene	Butadiene	Transition state
LUMO	anti-symmetric 0.17733 a.u.	symmetric 0.12036 a.u.	symmetric 0.02316 a.u.
HOMO	symmetric -0.36989 a.u.	anti-symmetric -0.31857 a.u.	anti-symmetric -0.32394 a.u.

From the energy values shown above it can be deduced that the reaction follows normal energy demand. The orbitals that interact to form the bonding MO are the HOMO of the diene (cis-butadiene) and the LUMO of the dienophile (ethene), since their linear combinations lowers the total energy of the molecule the most. It can be also confirmed by the symmetries of the HOMO and LUMO of the transition state. According to Woodward-Hoffman rules, which are used to determine if a pericyclic reaction is allowed, the orbital symmetries are preserved during the reaction. Therefore, symmetric HOMO of the transition state has to be formed of two symmetric orbitals which, as previously said, are HOMO of cis-butadiene and LUMO of ethene. Consequently, the LUMO of the transiton state is formed of the HOMO of ethene and LUMO of cis-butadiene.

The reaction of cyclohexa-1,3-diene with maleic anhydride

In order to study the regioselectivity of Diels Alder reaction, the cycloaddition of cyclohexa-1,3-diene with maleic anhydride was modelled. In this case cyclohexa-1,3-diene (diene) is the electron rich molecule, whereas maleic anhydride (dienophile) is the electron poor molecule. In contrast to the previously studied reactions, this one is asymmetrical, meaning that there are two approach trajectories. It result in two different transition states: exo- and endo-, which have different geometries. Their structures, MO's and relative energies were studied in order to determine the relative energy levels of HOMO and LUMO, as well as the preferred reaction pathway.

The structures of both transtion states were obtained starting with optimising maleic anhydride and cyclohexa-1,3-diene using the DFT/6-31G method. They were used to construct guess structures by setting the distance of 2.2 Å and aligning the molecules in the two possible orientations differing by a 180° rotation of one of the reactants. They were then optimised to a transition state (TS Berny) using AM1 semi-empirical method, followed by the frequency calculation using the same method. The negative frequency together with the IRC path proved that the obtained molecules were transition states.

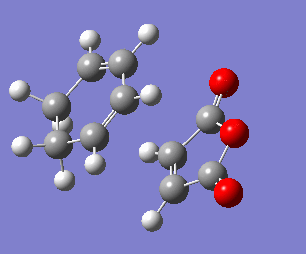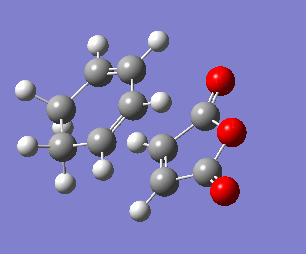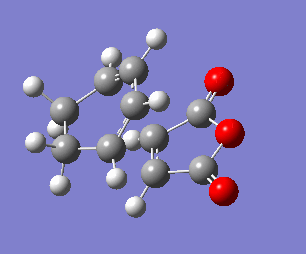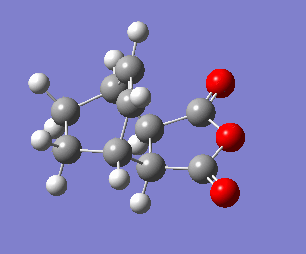
Exo transition state

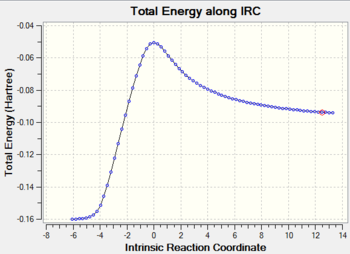
The exo transition state structure was optimised first. Its energy and the negative frequency were found to be -0.05042001 a.u and -810.87 cm^-2, respectively. The imaginary frequency is shown below, together with the IRC pathway of the reaction. It can be seen that the negative frequency corresponds to a transition state and that the reaction occurs via a concerted mechanism. Similarly to the reaction of ethene with cyclohexane, the TS was calculated in the opposite direction, i.e. from products to reactants.Therefore, the IRC graph is reversed: the left side corresponds to the product of DA addition, and the right side corresponds to maleic anhydride and cyclohexa-1,3-diene.

Animation of the reaction forming exo transition state	IRC plot of the reaction	Visualisation of the negative frequency

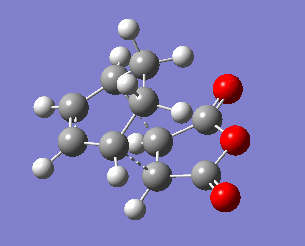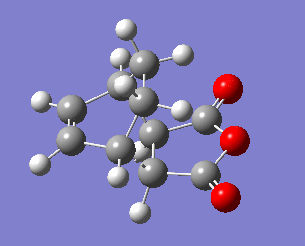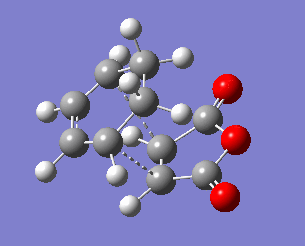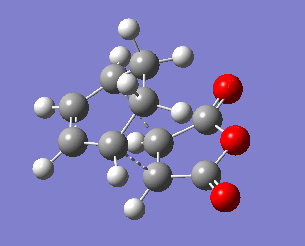To analyse the geometry and the connectivity of the exo transition state the some of the bond distances were determined and summarised in the table below. Most importantly, the bond lengths of C3-C9 and C4-C8 are both equal to 2.171 Å, which is (similarly to the example of cis-butadiene reacting with ethene) longer than a single bond length but shorter than the sum of van der Waals radii of two carbon atoms. It clearly supports the presence of a favourable interaction, which, however, cannot be considered as a single bond. Moreover, the bond distances between the carbon atoms involved in the ring that is being formed are all somewhere between the single bond distance (1.54 Å) and the double bond distance (1.34 Å), suggesting delocalised electrons.

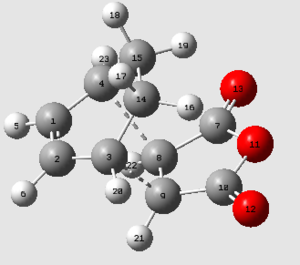
Exo transition state
C3-C9	C1-C2	C2-C3	C8-C9
2.171	1.397	1.394	1.410

Endo transition state

The endo transition state differs from exo by the orientation of the approaching molecules. In the animations below it can be noticed that the double bond is being formed above the approach trajectory, in contrast to the exo structure in which it was being formed below it. The energy of this transition state was found to be -0.5150480 a.u. and the negative frequency was -806.39 cm^-2. In this case the IRC path was calculated from reactants to the products, hence it has the expected energy profile: with the left hand side corresponding to the adduct that is significantly lower in energy.

Animation of the reaction forming endo transition state	IRC plot of the reaction	Visualisation of the negative frequency

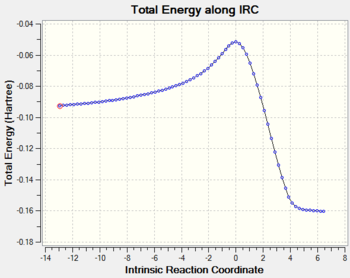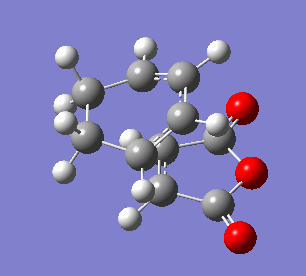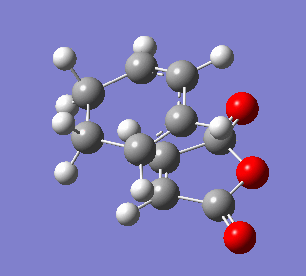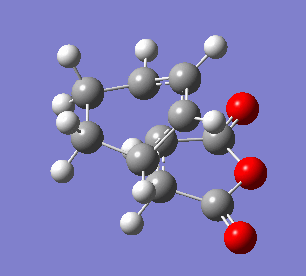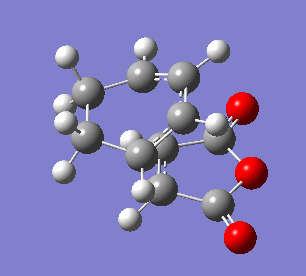In the table below important bond lengths were shown. Similarly to the exo transition state, electron delocalisation can be observed, as well as the positive interaction between C4 and C9 (accordingly: C3 and C8). The distance between them is longer than a single bond but significantly shorter than the sum of two carbon van der Waals radii.

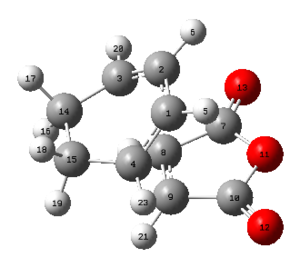
Endo transition state
C4-C9	C1-C2	C2-C3	C8-C9
2.162	1.397	1.393	1.408

Comparsion of MO geometries, activation energies and stabilities of exo and endo products

In order to determine the preferable product of the Diels-Alder reaction, the relative energies of the products and the activation energies for the transition states were analysed. The summary of the energies (in the units a.u.) of the reactants and products can be seen in the table below:

maleic anhydride	cyclohexa-1,3-diene	sum of reagents	exo TS	endo TS	exo product	endo product
-0.12182423	0.03495306	-0.08687117	-0.05042001	-0.05150480	-0.15990916	-0.16017043

(It looks like your energy for cyclohexadiene is incorrect. Looking at your log file it seems like this is the calculation for benzene Tam10 (talk) 15:24, 23 November 2015 (UTC))

It its clearly seen from the energies of the products that the endo structure is more stable since it has a lower energy, meaning that it is the thermodynamic product. The activation energies for the Diels-Alder adduction can be calculated by subtracting the energy of the sum of reagents from the energy of the TS structure and converting it to kJmol^-1 (1 a.u.mol^-1 = 2625.4 kJmol^-1). The results of the calculations are: 95.70 kJmol^-1 for the exo TS and 92.85 kJmol^-1 for the endo product. The data proves that the endo product is also the kinetically favourable product, since it has a lower activation energy.To justify these results, the bond distances and the geometries of HOMO and LUMO of the transition states were investigated.

Exo transition state	Endo transition state

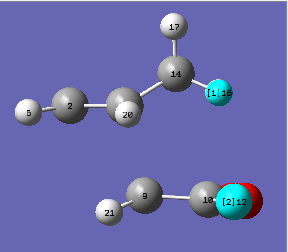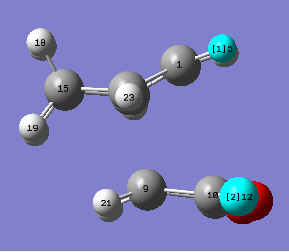The structures above are previously optimised endo and exo transition states. The distances between the carbonyl oxygen atoms in the maleic anhydride reactant and the closest hydrogen atom on the cyclohexa-1,3-diene are 3.317 Å (H5-O12) for the endo TS and 2.693 Å (H16-O12) for the exo TS. Knowning the van der Waal radii of oxygen and hydrogen (1.52 Å and 1.20 Å, respectively) it can be observed that the distance in the exo transition state is lower. It contributes to the fact that this form is more strained which explains why it has a higher activation energy.

The HOMO and LUMO of both transition states can be found here. All of the shown orbitals (HOMO's and LUMO's of endo and exo transition states) are antisymmetric. Moreover, in both molecules it can be seen that there is that the HOMO has nodal planes passing only through atoms, whereas in LUMO an additional nodal plane between two approaching reagents is observed, showing that these are the excited states. In the endo transition state, a significant secondary orbital overlap is observed between C=C π orbital and π* orbital of the carbonyl groups. It is due to the delocalisation of electrons between the two orbitals which are close together, which lowers the overall energy of the molecule and causes the endo product to be more kinetically favourable. To compare, the exo transition state no "secondary orbital overlap" is observed, since C=C π orbital is too far from C=O π* for any major overlap to occur. Thus, no additional favourable interactions are observed.

Conclusions

In this experiment, three pericyclic reactions were studied computationally: Cope rearrangement of 1,5-hexadiene and two Diels-Alder reactions: cis-butadiene with ethene and maleic anhydride with cylcohexa-1,3-diene.

The first reaction was computed using HF/3-21G and DFT/6-31G methods. Both computations resulted in the same geometries of the structures, showing that the chair TS is involved in the prefered pathway. Nevertheless, only the activation energy calculated using the higher level of theory (DFT/6-31G) was reasonably close to the literature value (other one being ~30% higher). It was also found out that gauche3 conformation is the one of lowest energy due to a favourable overlap of π orbitals on the terminal double carbon-carbon bonds.

Both of the Diels-Alder cycloadditions were computed using AM1 semi-empirical method, which is faster but less accurate than DFT/6-31G or HF/3-21G. It was chosen due to higher complexity of the molecules involved in the reactions. In both of them, the length of the forming bonds was measured and proved to be longer than a single C-C bond but shorter then the sum of two van der Waals radii, which rationalises the favourable interaction present in transition state. Furthermore, the MO's involved in the cycloaddition of cis-butadiene and ethene were analysed to prove that the reaction is allowed by showing that the orbital symmetries were preserved.

Finally, the selectivity of the Diels-Alder reaction was investigated on the example of the reaction between maleic anhydride and cyclohexa-1,3-diene. It turned out that the endo structure was more kinetically and thermodynamically stable. The reasons might be secondary orbital overlap present in the endo TS but absent from exo, as well as the strain observed in the exo structure. Nevertheless, the difference in the energies of the products supporting that endo is the thermodynamic product is very small and might be questionable, since the computational methods make a number of approximation, the first one being aforementioned Born Oppenheimer approximation. Moreover, the structures analysed are only guesses and even if they are optimised, there might be a slightly different conformation yielding a lower energy, as seen for the 1,5-hexadiene reaction. Finally, the computations examine only a single molecule, which neglects a variety of intermolecular interactions that are present in a real-life system.

References

<references>