Rep:Mod:to1011
Part 1:
Conformational analysis using Molecular Mechanics
The Hydrogenation of Cyclopentadiene Dimer
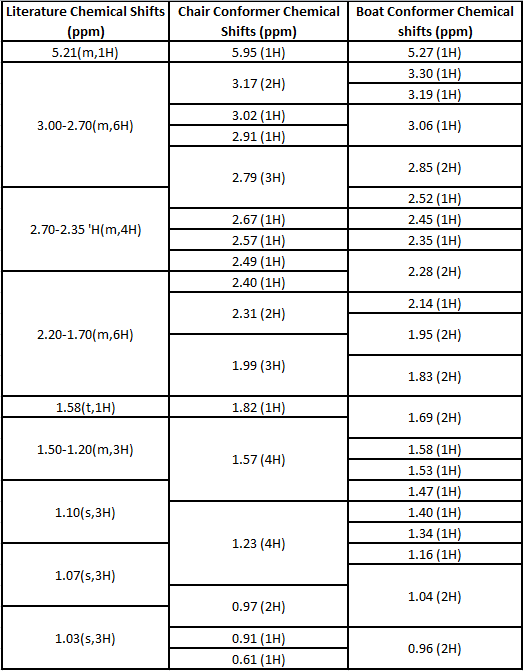
Cyclopentadiene dimerises to form the endo product (2) rather than the exo product (1). Hydrogenation of the endo dimer leads to the two possible dihydro derivatives, (3) or (4). By modelling all four molecules it can be deduced which are the more thermodynamically stable products and whether these are the same as those found experimentally. The molecules were modeled by using the MM2 force field in ChemBio3D Ultra and the results are shown below:
| Exo Dimer (1) | Endo Dimer (2) | Product (3) | ||
|---|---|---|---|---|
| Stretch (kcal/mol) | 1.2850 | 1.2509 | 1.2348 |
1.0965 |
| Bend (kcal/mol) | 20.5804 | 20.8477 | 18.9380 |
14.5243 |
| Stretch-Bend (kcal/mol) | -0.8380 | -0.8358 | -0.7609 |
-0.5494 |
| Torsion (kcal/mol) | 7.6555 | 9.5109 | 12.1241 |
12.4974 |
| Non-1,4 VDW (kcal/mol) | -1.4173 | -1.5439 | -1.5015 |
-1.0701 |
| 1,4 VDW (kcal/mol) | 4.2334 | 4.3201 | 5.7289 | 4.5126 |
| Dipole/Dipole (kcal/mol) | 0.3775 | 0.4476 | 0.1631 |
0.1406 |
| Total Energy (kcal/mol) | 31.8764 | 33.9975 | 35.9266 |
31.1520 |
Exo Dimer (1) and Endo Dimer (2)
It can be seen from these results that the exo dimer (1) has the lower energy and hence is more thermodynamically stable than the endo dimer (2). This is contrary to the experimentally seen results and hence it can be said the dimerisation of cyclopentadiene is under kinetic control and therefore the transition state of the endo dimer is stabilised and is lower in energy than the transition state in the exo dimer. This can be explained by looking at the interaction of the orbitals between the two cyclopentadiene molecules in the transition state. In the exo transition state the HOMO and LUMO interact to form bonds but there is no extra stabilization due to the orientation of the two molecules. In the endo transition state the HOMO and LUMO interact to form bonds but there is extra stabilization of the the HOMO and LUMO and hence the energy of the endo transition state is lowered. Looking further at the results it can be seen that the main reason that the exo dimer is more thermodynamically stable is because it has a lower torsion energy. The closeness of the two carbon rings in the endo dimer creates unfavorable Pauli repulsions, increasing the torsional energy.
Products (3) and (4)
Looking at the results for the hydrogenation products of the endo dimer (3) & (4), product (4) has the lower energy and hence is the thermodynamically more stable product. It is known from literature that the favored hydrogenation product is product (4)[1] and hence the reaction is under thermodynamic control. It can be seen that the biggest difference is between the bend energies with product 3 have a greater bend energy by ~4 kcal/mol. If the double bond in product (3) is considered, the C-C-C bond angle of the sp2 hybridized Carbon is 107.6°. When this is compared to the ideal sp2 bond angle of 120.0° there is a difference of 12.4°. The C-C-C bond angle of the sp2 in product (4) is 113.0° a difference of 7.0°. Therefore the bend energy of product (4) is reduced and this is why it is the more stable hydrogenation product.
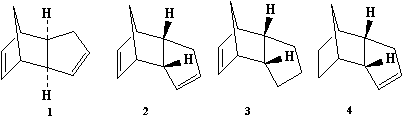
An important intermediate in the synthesis of the ovarian cancer treatment drug, Taxol, is one of the two atropisomers (9) or (10). Atropisomers are stereoisomers caused by the restriction of rotation around a single bond. This leaves (9) with the carbonyl group facing upwards and (10) with the carbonyl group facing down. It has also been found that the functionilization of the alkene in the intermediate occurs slowly. The objective was to find which of the atropisomers is more stable and to explain the speed of the reactivity of the alkene.
The molecules were modeled by using the MM2 force field in ChemBio3D Ultra. Two isomers of each atropisomer were found, one with a cyclohexane ring chair conformer and the other with a cyclohexane ring twist boat conformer. It is known that the twist boat conformers will have higher energies than the corresponding chair conformers so their energies weren't computed.This is the twist boat for intermediate (9) and this is the twist boat for intermediate (10). The results for the chair conformers are shown below:
| Intermediate (9) | ||
|---|---|---|
| Stretch (kcal/mol) | 2.7847 | 2.6205 |
| Bend (kcal/mol) | 16.5410 | 11.3391 |
| Stretch-Bend (kcal/mol) | 0.4304 | 0.3432 |
| Torsion (kcal/mol) | 18.2512 | 19.6719 |
| Non-1,4 VDW(kcal/mol) | -1.5521 | -2.1617 |
| 1,4 VDW (kcal/mol) | 13.1092 | 12.8721 |
| Dipole/Dipole (kcal/mol) | -1.7248 | -2.0023 |
| Total Energy (kcal/mol) | 47.8395 | 42.6828 |
It can be seen that intermediate (10), with the carbonyl group facing downwards, is the more thermodynamically stable atropisomer. Comparing the energies of the two atropisomers, the biggest difference is between the bend energies. If the sp2 hybridized carbon (the carbonyl carbon) is considered, then the C-C-C bond angle for intermediate (9) is 126°, a 6° degree difference from an ideal bond angle of 120°. However the C-C-C bond angle on the sp2 hybridized carbon is 120° for intermediate (10), equal to the ideal bond angle. This means the bend energy of intermediate (10) is reduced and hence it is the more thermodynamically stable product.
As stated before, it is known that the functionilization of the alkene in the intermediate occurs slowly. This is because the alkene belongs to a class called hyperstable alkenes. Hyperstable alkenes contain less strain than the parent alkene and hence makes them more unreactive[2]. This is due a greater stability as a result of the cage like nature of the alkene[3]and a destabilization of the parent alkene as a result of transannular strain between Hydrogen atoms[3].
Spectroscopic Simulation using Quantum Mechanics
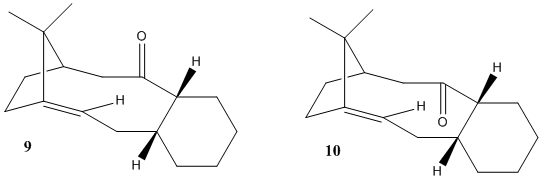
The molecules (17) and (18) are derivatives of the intermediates looked at in the previous section. Their 1H and 13C NMR data has been published and the objective is to simulate the spectroscopic data for 1 molecule and then compare it with the literature[4]. The chosen molecule was (18) because this was the more thermodynamically stable molecule (as found previously). Molecule (18) has many conformers due to the nature of the cylohexane ring but only 2 were chosen to compare with the literature. The first is a chair conformer and the other is a boat conformer. Their geometries were then minimized using the MM2 force field in ChemBio3D and then their spectra were calculated using Gaussian on the HPC system. For molecule (18), the literature[4] 1H NMR is 300MHz,C6D6 and 13C is 75MHz, C6D6. For the 13C data, the shifts of those carbons next to Sulphur atoms had to be corrected, due to spin-orbit coupling errors, by -3ppm. Both the literature and computed values are shown for the 1H NMR in the table below, the data is published here: DOI:10042/25752 DOI:10042/25753
1H NMR Table for both literature and quantum mechanically computed data.


First, comparing the literature data[4] to the computed chair conformer data, it can be seen that the computed alkene singlet is at a much greater chemical shift than the corresponding literature alkene singlet. This is a trend that is continued between most chair conformer data and literature data in that they do not correlate well.
However if the literature data & the computed boat conformer data are compared, a much better correlation is found. For example, the two alkene singlets are almost identical, being within 0.1ppm of each other. If it is assumed that that multiplets stated in the literature are a result of the overlap of different signals, then the degeneracies between the two data sets correlate well. There is also a proton that lies at exactly 1.58ppm in both the literature and computed data.
This correlation infers that the sample that the NMR was run on in the literature was predominantly the boat conformer.
The computed boat conformer data and chair conformer data can also be compared, where it is seen that the two data sets, although similar, do differ slightly. This is a result of the different geometries of the two conformers which changes the relative positions of the hydorgen atoms.
Both the literature and computed values are shown for the 13C NMR in the table below:


| Literature Chemical Shifts (ppm) | Chair Conformer Chemical Shifts (ppm) | Boat Conformer Chemical shifts (ppm) |
|
211.49 |
211.06 |
210.58 |
|
148.72 |
147.93 |
148.35 |
|
120.90 |
120.04 |
118.91 |
|
74.61 |
90.64 |
85.71 |
|
60.53 |
60.46 |
67.85 |
|
51.30 |
54.77 |
55.87 |
|
50.94 |
53.94 |
55.46 |
|
45.53 |
49.54 |
49.94 |
|
43.28 |
49.15 |
45.00 |
|
40.82 |
43.67 |
41.04 |
|
38.73 |
41.90 |
41.97 |
|
36.78 |
38.74 |
37.35 |
|
35.47 |
38.52 |
35.19 |
|
30.84 |
34.05 |
30.92 |
|
30.0 |
33.62 |
28.87 |
|
25.56 |
28.10 |
28.59 |
|
25.35 |
26.45 |
25.73 |
|
22.21 |
24.41 |
25.16 |
|
21.39 |
22.62 |
23.39 |
|
19.83 |
21.57 |
20.98 |
Comparing both the computed boat and chair NMR data to the literature values[4], it can be seen that they both correlate relatively well. However the literature value at 74.61 ppm, which arises due to the carbon bonded to two sulphur atoms, differs by ~15 ppm for the chair conformer and ~10ppm for the boat conformer. Such a big difference leads to a conclusion that the literature value has been misreported. Aside from this, the biggest difference between the literature and computed data is ~7ppm and there is no clear indicator which conformer best agrees with the literature. Comparing the two computed data sets, the values all lie within ~5 ppm showing that although the geometries change between conformers, the relative postions of the carbon atoms do not change as much as the hydrogen atoms.
Part 2:
The Crystal Structures of the Shi and Jacobsen Catalysts
The crystal structures of the two pre catalysts were searched in the Cambridge Crystal Database using Conquest. The objective was to measure the C-O bond lengths at the anomeric centres for the Shi pre catalyst and to discuss the close approach of the adjacent t-butyl groups on the rings for the Jacobsen pre catalyst.
ShiCatalyst |
It can be seen from the Jmol model that the precatalyst (and hence the catalyst) has one 5 membered ring above the plane of the cyclohexane ring and one 5 membered ring below it. For the alkene to be functionalized to an epoxide it must approach close to the oxirane group and hence for cis-alkenes there will be a much greater steric hindrance than when the trans-alkene approaches.
Looking at the C-O bond lengths at the two anomeric centres it can be seen that two have the same length whereas two have different lengths. For the two with same length (1.40Å), the axial oxygen on the cyclohexane ring cannot donate its lone pair into the C-O σ* orbital because the σ* orbital is not in the right orientation. This is possible in the five membered ring, and given that an antibonding orbital is populated, the bond becomes weaker and longer.
JacobsenCatalyst |
The distance between the two tert-butyl Hydrogens can be seen as 2.69Å which implies a slight attractive Van der Waals interaction between the two. The close proximity of these tert-butyl groups prevents the approach of the alkene from that face and as the other two faces are also blocked by tert-butyl groups on the benzene rings, the alkene is forced to approach over the cyclohexane ring.
The Calculated NMR of the Product Epoxides
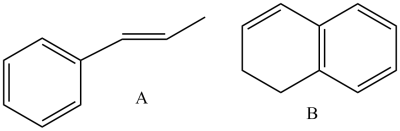
The two alkenes that were chosen to be epoxidized were trans-β-methylstyrene (A) and 1,2-dihydronapthalene (B). The resultant epoxides are (1R,2R)-trans-β-methylstyrene oxide, (1S,2S)-trans-β-methylstyrene oxide, (1R,2S)-epoxy-3,4-dihydronapthalene and (1S,2R)-epoxy-3,4-dihydronapthalene. Their geometries were first minimised using ChemBio3D and then run on Gaussian using the HPC to further minimise their geometries so that a computed NMR spectra could be produced. For (1S,2S)-trans-β-methylstyrene oxide the literature[5] 1H NMR is 400MHz CDCl3 and the 13C NMR is 100MHz CDCl3. Both the literature and computed values are shown in the table below, the data is published here: DOI:10042/25792 DOI:10042/25793

| Literature 1H (ppm) | Computed 1H (ppm) | Literature 13C (ppm) | Computed 13C (ppm) |
|---|---|---|---|
| 7.26 - 7.14(m, 5H) | 7.49 (3H) | 137.8 | 134.98 |
| 3.47 (1H) | 7.42 (1H) | 128.5 | 124.07 |
| 2.93 (1H) | 7.30 (1H) | 128.1 | 123.33 |
| 1.35 (3H) | 3.41 (1H) | 125.6 | 122.80 |
| - | 2.78 (1H) | 59.6 | 122.73 |
| - | 1.67 (1H) | 59.1 | 118.4 |
| - | 1.58 (1H) | 18.0 | 62.3 |
| - | 0.71 (1H) | - | 60.57 |
| - | - | - | 18.84 |
If both the 1H and 13C computed and literature NMR data are compared it can be seen that they correlate very well with all the degeneracies matching between the two. For the 13C data, there are more carbon environments in the computed data than in the literature data, this is due to two carbons in the literature NMR overlapping due to such a close chemical shift, producing one peak on the spectrum. Given the correlation between the literature and computed data, it can be said that the epoxide has been modelled correctly.
For (1R,2S)-epoxy-3,4-dihydronapthalene the literature [6] 1H NMR is 400MHz CDCl3 and the 13C NMR is 100MHz CDCl3. Both the literature and computed values are shown in the table below, the data is published here: DOI:10042/25795 DOI:10042/25794
| Literature 1H (ppm) | Computed 1H (ppm) | Literature 13C (ppm) | Computed 13C (ppm) |
|---|---|---|---|
| 7.28 (d, 1H) | 7.49 (1H) | 136.7 | 133.83 |
| 7.08-7.17 (m,2H) | 7.38 (2H) | 132.6 | 130.37 |
| 6.98 (d,1H) | 7.19 (1H) | 129.5 | 125.55 |
| 3.74 (d,1H) | 3.59 (2H) | 128.4 | 123.82 |
| 3.62 (m,1H) | 2.87 (1H) | 128.4 | 123.41 |
| 2.68(m,1H) | 2.26 (1H) | 126.1 | 121.43 |
| 2.44(m,1H) | 2.21 (1H) | 55.1 | 56.43 |
| 2.30(m,1H) | 1.56 (1H) | 52.7 | 54.81 |
| 1.65(m,1H) | - | 24.4 | 28.03 |
| - | - | 21.8 | 24.94 |
If both the 1H and 13C computed and literature NMR data are compared it can be seen that they correlate very well, with the maximum difference between 1H chemical shifts ~0.2ppm and ~5ppm for 13C chemical shifts. The degeneracies are also the same. This implies that the epoxide has been modelled correctly.
The Optical Rotary Power of the Product Epoxides
The optical rotations for the two epoxides were then calculated by taking the output files from the NMR and calculating the ORP in gaussian via the HPC. Looking specifically at light of wavelength 589nm, only one enantiomer of each epoxide was considered as the opposite enatiomer would have an equal and opposite optical rotation. This is summarised in the table below:
| (1S,1S)trans-β-methylstyrene oxide DOI:10042/25796 | (1R,2S)-epoxy-3,4-dihydronapthalene DOI:10042/25808 |
| -47.09° | 156.02° |
Unfortunately this value cannot be compared to literature values as various postive and negative rotations are quoted for each enantiomer. However when the epoxides are created in experiment 1S the absolute configuration of the molecule created can be assigned by measuring the optical rotation in the laboratory and then comparing it to the values quoted above.
Using the Calculated Transition States to Predict the Favoured Enantiomer
The transition states of the R,R and S,S enantiomers for trans-β-methylstyrene oxide with the Shi catalyst were modelled to find the the gibbs free enrgies. By finding the change in gibbs free energies between the transition states of the enantiomers, a ratio of S,S product to R,R product could be found. Given there were a range of different transition states the ones with lowest energy for each enantiomer were found and by using the equation ΔG=-RTlnK, the ratio of the two products could be found. The values are summed up in the table below:
| ΔG value for the ratio of S,S : R,R enantiomers | Equilibirium constant, K, for the ratio of S,S : R,R enantiomers |
|---|---|
| -20.22 kJ / mol | 3488 |
Given that this ratio is very large, it can be said that (1s,2S)-trans-β-methylstyrene is formed predominantly over the other enantiomer.
Investigating the Non-covalent Interactions in the Active-site of the Transition State
Orbital |
Investigating the Electronic Topology (QTAIM) in the Active-site of the Transition State
Suggesting New Candidates for Investigation
References
- ↑ G. L. , Z. M. , L. W. , X. Z. , S. Z. , Ind. Eng. Chem. Res., 2006, 45, 8814 DOI:10.1021/ie060660y
- ↑ A. B. M. , P. v. R. Schleyer, J. Am. Chem. Soc., 1986, 108, 3960 DOI:10.1021/ja00274a016
- ↑ 3.0 3.1 W. F. M. , P. V. R. Schleyer, J. Am. Chem. Soc., 1981, 103, 1900 DOI:10.1021/ja00398a003
- ↑ 4.0 4.1 4.2 4.3 L. A. P. , N. A. P. , D. T. , G. D. M. , R. D. Rogers, J. Am. Chem. Soc., 1990, 112, 283 DOI:10.1021/ja00157a043
- ↑ A. Schmid, K. Hofstetter, H. Feiten, F. Hollmann, B. Witholt, Advanced Synthesis & Catalysis, 2001, 343, 732 DOI:<732::AID-ADSC732>3.0.CO;2-Q 10.1002/1615-4169(200108)343:6/7<732::AID-ADSC732>3.0.CO;2-Q
- ↑ Keith Smith, Chia-Hui Liua and Gamal A. El-Hitia Organic & Biomolecular Chemistry, 2006, 004, 917-927 DOI:10.1039/B517611P