Rep:Mod:tmlkmcd
Computational Labs - (Module 1) Organic Chemistry
Author: Thomas McDevitt
Note: This page is best viewed using Mozilla Firefox.
Abstract
Molecular modelling is a computational method used to calculate common properties of molecules. These can extend to spectroscopic properties, but it mainly concerns itself with the computing of geometric properties of a molecule by calculating a simple sum of the individual bond properties, namely:
- Compressive/tensile strain
- Bayer strain (bending energy)
- Pitzer strain (torsional energy)
- Van der Waals forces (as a function of the internuclear separation; the Lennard Jones potential)
No wavefunctions are taken into account; this is a purely classical method to calculating properties and in doing so, the ideal method can be found by iterating until a conformational minima is found.
This module aims to explore the capabilities of molecular modelling, to expose the weaknesses and overcome them by adding alternative mechanics which will provide reasonable approximations to the true answers that don't involve fully-fledged quantum calculations as these would not be completed in a reasonable amount of time.
Throughout this module, the Allinger MM2 method is used. It assigns an energy to its calculated conformational minima which can be used to effectively compare isomers but it should be noted that it is not as an absolute value in any way since this energy has no thermodynamic relevance.
The Hydrogenation of Cyclopentadiene Dimers
|
|||
Total energy: 6.48 kcal/mol |
Cyclopentadiene is an unsaturated organic molecule that can act as both the diene and the dienophyl in an intermolecular Diels-Alder reaction, which it undergoes as it dimerizes to form dicyclopentadiene. In theory, there are two possible outcomes of this - one is that it forms the endo-Diels-Alder product and the other is that the exo-Diels-Alder product is formed.
 (Molecule 1) | 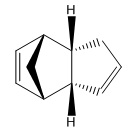 (Molecule 2) |
However, in practice, the endo- product is formed preferentially. This can be rationalised by exploring both potential products and their properties using molecular modelling.
|
| |||||||
| Stretch: | 1.29 | 1.25 | ||||||
| Bend: | 20.59 | 20.87 | ||||||
| Stretch-Bend: | -0.84 | -0.84 | ||||||
| Torsion: | 7.67 | 9.51 | ||||||
| Non-1,4 VDW: | -1.43 | -1.56 | ||||||
| 1,4 VDW: | 4.23 | 4.32 | ||||||
| Dipole/Dipole: | 0.38 | 0.45 | ||||||
| Total: | 31.88 | 34.00 |
Note: energy values given in kcal/mol.
 |
 |
From these results, it can be seen that the majority of the increased energy of the endo- product arises from torsional strain, which arises as a result of the dihedral angle between atoms which are three bonds apart being locked closer to the high energy eclipsed conformation instead of the preferred staggered conformation. This can be seen in the molecules in the eclipsing conformation of the two groups with double bonds (which are more sterically hindering than the protruding CH2 group) in the endo- dimer which is avoided in the exo- case.
The lower energy of the exo- product renders it the thermodynamic product - however, the endo- product is formed instead since the path to the endo- product passes through a sterically unfavourable overlap between both cyclopentadiene monomers. The final exo- product is lower, but since the formation of the endo- product has a much lower kinetic barrier (lower activation energy), under non-equilibrating conditions it will be formed over the other.
Hydrogenation of the endo- dimer gives two products (without extended hydrogenation, which leads to complete saturation of the molecule).
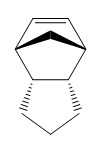 |
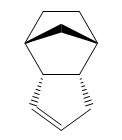 |
|
|
|||||||
| Stretch: | 1.24 | 1.10 | ||||||
| Bend: | 18.91 | 14.52 | ||||||
| Stretch-Bend: | -0.76 | -0.55 | ||||||
| Torsion: | 12.18 | 12.49 | ||||||
| Non-1,4 VDW: | -1.53 | -1.06 | ||||||
| 1,4 VDW: | 5.74 | 4.51 | ||||||
| Dipole/Dipole: | 0.16 | 0.14 | ||||||
| Total: | 35.94 | 31.16 |
This time, the torsion energies are far closer together, but the bending interaction raises the energy of molecule 3 to the point at which its energy is much higher. As a result, it can be concluded that upon hydrogenation of a cyclopentadiene dimer, product 4 will be produced.
Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD+ analogue)
|
Molecule 5 has been discovered to react with Grignard reagent MeMgI in a stereospecific reaction creating the enantiomeric product molecule 6 with a selectivity of about 95%[1] . Molecule 5 and its conformation can be seen to the left. It was drawn into BioChem3D and the energy minimized using a MMFF94 method due to a bug in the MM2 method with analysing the effect of a positivily charged nitrogen. A total energy of 57.44 kcal/mol was obtained. It can be seen that the carbonyl oxygen is slightly out of the plane of the benzyl group (dihedral angle = 15o). When considering the mechanism of the reaction, it is easy to see that the carbonyl has a steering effect on the attack of the nucleophilic methyl species offered by Grignard reagents, being the cause of the stereospecificity of this reaction. |
|||

|
Molecule 7 was then drawn and optimized using the MMFF94 method as was done with molecule 5. A total energy of 98.28 kcal/mol was obtained (differing to the less accurate 62.76 kcal/mol obtained using the MM2 method). Again, the carbonyl oxygen falls out of the plane of the nearby phenyl group but in the opposite direction this time, with a dihedral angle of -37o. The higher energy corresponds to the much higher torsional strain caused by linking a less flexible phenyl group to the seven-membered ring (as opposed to the cyclopentane group at the corresponding position in molecule 5) and the steric clash of the secondary butyl group attached to the amine adjacent to the carbonyl carbon, the latter of which effects a the higher dihedral angle of the carbonyl oxygen as can be seen in the diagram on the right. |
|
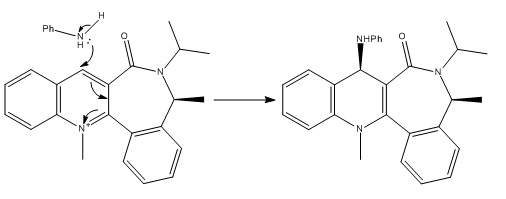
In both of these cases, the seven-membered ring is essentially locked into its conformation[1][2]. It has the potential to be able to undergo ring-flipping under extreme conditions but at room temperature it is hindered from switching conformations by a large kinetic barrier induced by steric repulsions, rendering it an atropisomer. The isomerism that results from this drives both reactions in the above examples to their shown stereospecificity and as such the reactions are said to be atropenantioselective.
Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol
| |||
Carbonyl faces upwards. |
| |||
Carbonyl faces downwards. |
One of the key intermediates in the synthesis of taxol comes in two isomers - one of which involves the carbonyl group facing upwards (molecule 9, left) and the other involves the same carbonyl group facing downwards (molecule 10, right). Molecular modelling (MM2) will be used to determine which of these is the lower energy form. The resulting energy calculations are as follows.
| Stretch: | 2.54 | 2.56 |
| Bend: | 11.71 | 10.66 |
| Stretch-Bend: | 0.39 | 0.32 |
| Torsion: | 19.02 | 19.67 |
| Non-1,4 VDW: | -0.85 | -1.30 |
| 1,4 VDW: | 12.42 | 12.54 |
| Dipole/Dipole: | 0.14 | -0.18 |
| Total: | 45.38 | 44.27 |
| |||
| An interesting thing to note is that molecule 9 can also be minimized with the cyclohexane ring in a twist-boat conformation. Total energy: 50.05 kcal/mol |
It can be seen that molecule 10 has lower energy, hence it can be deduced that this is the isomer that predominantly exists and that molecule 9 will preferentially isomerise to form molecule 10 under the right conditions. However, these are atropisomers, meaning that (particularly at low temperatures) they can be isolated from each other as they are prevented from isomerising to their alternate forms by kinetic barriers which they can't overcome without enough energy.
The primary difference in the two energies of these molecules is the bend energy; the instability induced when bonds are formed at angles away from their optimum value (e.g. an sp3 hybridised carbon favours all of its bond angles to be 109o28' (in a tetrahedral geometry) whereas any bonds bent as such that they deviate from this optimum value will raise the energy. This is difficult to observe by eye in a system with so many molecules.
Another interesting thing to consider is how the olefin group in these molecules is placed. Bredt's rule states:
| “In polycyclic systems having atomic bridges, the existence of a compound having a carbon-carbon or carbon-nitrogen double bond at a bridgehead position is not possible, except when the rings are large, because of the strain which would be introduced in its formation by the distortion of bond angles and/or distances. As a corollary, reactions which should lead to such compounds will be hindered or will give products having other structures.”[3] |
One may argue that molecules 9 and 10 are large enough to accommodate Bredt's rule, though numerous other examples of bridgehead olefins in medium-sized ring systems have since been isolated since the discovery of hyperstable olefins[4] - alkene groups which have negative strain energies rendering them even more stable than their parent saturated hydrocarbons. In this case, the hydrogenated versions of molecules 9 and 10 (labelled 9b and 10b respectively) will be drawn out and optimized using the MM2 method in BioChem3D and the energies examined.
| Unsaturated Energy / kcal mol-1 | Saturated Energy / kcal mol-1 | OS / kcal mol-1 | |
| Molecule 9 | 45.41 | 54.41 | -9.00 |
| Molecule 10 | 54.95 | 60.97 | -6.02 |
Here, 'OS' refers to the olefin strain energy[4][5], in these cases the stabilisation effected onto the molecule by the unsaturation with respect to the parent hydrocarbon. This extra stability is not caused by steric hindrance or extra π-stability, but due to the stability of the cage-like structure[5] and, in these cases, hydrogenation of the olefin group would change the hybridisation of the relevent bridgehead carbons and put more strain onto the rings, raising the energy of the molecule. As such, they are resilient to hydrogenation and in general would be very unreactive.
Modelling Using Semi-empirical Molecular Orbital Theory
| |||
We move away now from the classical approach to molecular modelling. This section exposes and overcomes the weaknesses in the MM2 method used by introducing basic quantum mechanics into what has been a purely classical solution up to this point.
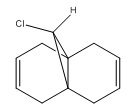
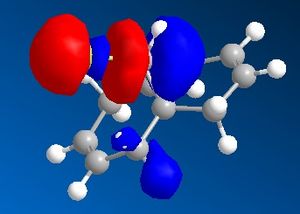
9-Chloro-1,4,5,8-tetrahydro-4a,8a-methanonaphthalene was drawn out and optimized using the MM2 method. The molecular orbitals were then calculated using the MOPAC/PM6 method. The HOMO -1, HOMO, LUMO, LUMO +1 and LUMO +2 were then examined in more detail.
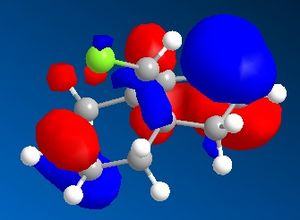 |
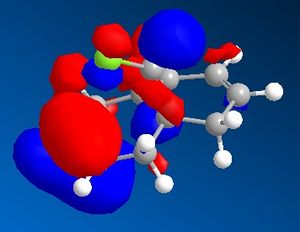 |
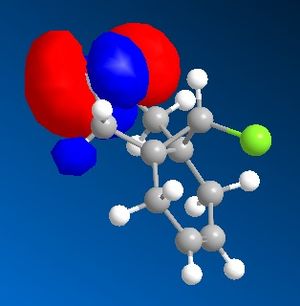 |
 |
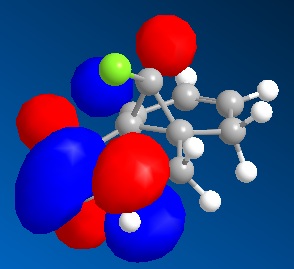 |

The olefin anti- to the chlorine
has been hydrogenated.
From the calculated HOMO, it can be seen that there is a lot of electron density on the olefin group syn- to the chloride group whereas there is much less on the olefin group anti- to it. Therefore, the olefin group that is syn- with respect to the chloride will be a lot more electron dense and will be preferentially targetted by electrophiles such as dichlorocarbene or a peracid.
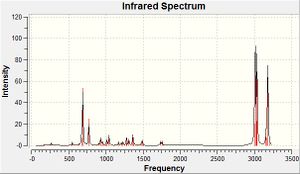
The frequencies of vibrations of molecules 12 and 13 were then calculated using the Imperial College SCAN and vibration/absorption frequencies recorded.
| C-Cl stretch | C=C olefin stretch | |
| Molecule 12[6] | 770.9 cm-1 | 1737.1 cm-1 (anti), 1757.4 cm-1(syn) |
| Molecule 13[7] | 775.0 cm-1 | 1758.1 cm-1 (syn) |
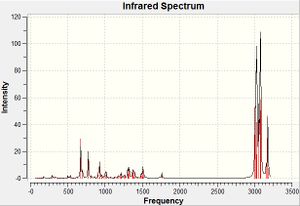
The syn- olefin stretching frequency shows very little change between spectra - what little change there is will simply be due to the minor changes in structure of the molecule. The anti- olefin stretching frequency disappears from molecule 12 to 13 since this is the functional group which is being changed, meaning the equivalent molecular stretch in 13 will correspond to that of a different functional group. The C-Cl stretch, however, has changed by a small yet considerable amount. The stretch occurs at a higher wavenumber (and as such, higher energy) potentially due to an interaction between the occupied anti-C=Cπ-orbital (HOMO -1) and the unoccupied C-Cl pσ*-orbital (LUMO +1) which can occur in molecule 12 as a donation of electrons from the C=Cπ-orbital into the C-Clσ*-orbital, lowering its bond order, making it more labile and hence lowering the wavenumber of the vibration. Upon hydrogenation of the olefin group in question, the symmetry of the C=C bond changes from π to σ, reducing if not eradicating this interaction, allowing the rigidity and hence wavenumber to rise again.
This interaction would also effect the strength of the olefin group anti- to the chloride. The lower wavenumber suggests that the bond has risen in stability due to the interaction.
Structure based Mini project using DFT-based Molecular orbital methods
Overview
This miniproject will discuss the stereospecific photochemical dimerisation of 2-butene DOI:10.1021/ja01030a066 . Other than fragmentation products, two primary products were obtained.
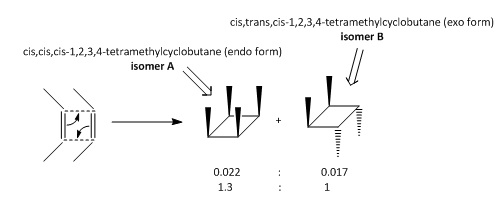 |
|
|
|
|
NMR will be the primary method to detect these compounds and tell them apart from each other. The lack of heteroatoms (and hence, very limited selection of identifiable functional groups) makes infrared spectroscopy less useful.
The Dominant Product
The two products were then drawn into BioChem3D and optimized using the MM2 and MMFF94 methods.
| Isomer A | Isomer B | |
| MM2 energy / kcal mol-1 | 34.86 | 32.80 |
| MMFF94 energy / kcal mol-1 | 22.93 | 20.11 |
Both methods calculate isomer B to have the lower energy, suggesting that it would be the predominantly formed product in this reaction. This is also the choice of product selected by chemical intuition when examining the transition states.
But-2-ene dimerises photochemically by a pericyclic reaction via a Möbius transition state. The two possibilities for the overlap are:
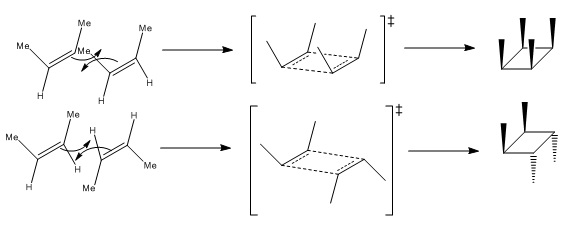 |
 |
It can be seen that isomer B is more kinetically accessible due to an unfavourable steric clash between the methyl groups which can be avoided to an extent by formation of the exo- isomer. However, the empirical data shows that endo- form is formed at the ratio of 1.3:1.0 (0.022:0.017)[11], contradicting what would be expected from computational stability calculations and chemical intuition upon considering the reaction mechanism.
This may be due to the fact that molecular modelling methods endeavor to find one single optimum geometry without taking into account conformational flexibility that occurs at room temperature (and almost all other experimental conditions).
Prediction of Spectroscopic Data
NMR Spectra - Isomer A
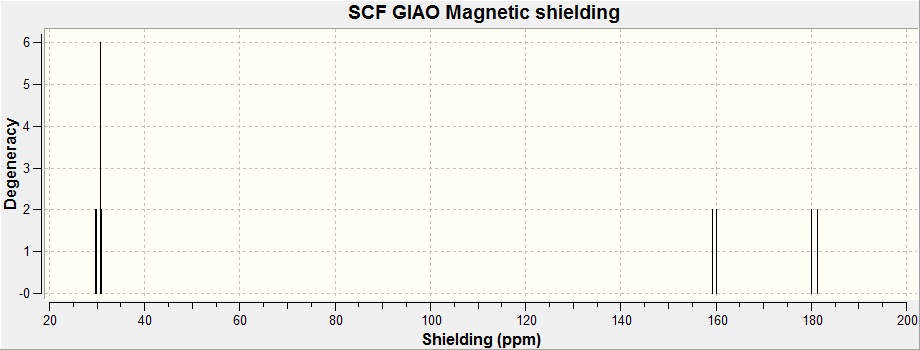
The computed NMR spectrum is below.
 |
| Carbon atom(s) | Computed δ / ppm[13] | Predicted δ in practice / ppm |
| 1, 4 | 160.56 | 162.03 |
| 2, 3 | 163.49 | 162.03 |
| 7, 8 | 181.78 | 183.46 |
| 5, 6 | 185.13 | 183.46 |
These chemical shifts make sense since carbon is a (marginally) more electronegative element than hydrogen [14] (Pauling electronegativity of carbon = 2.55; hydrogen = 2.2) ultimately giving rise to the 'methyl inductive effect' which will cause the methyl substituents to increase the shielding of the cyclobutane ring carbons slightly[15], lowering their chemical shift as seen by the computed spectra.
The computed spectrum has chemical shifts for the hydrogen entities within the molecule, but these won't be analysed in much detail since the peaks appear at about (30±2)ppm whereas the 1H peaks in literature appear at 0.87 (for the methyl protons) and 2.4 (for the vicinal ring protons)[11]. This exposes the errors involved in the method used for calculating 1H chemical shifts and that they aren't accurate enough to be useful.
NMR Spectra - Isomer B
 |
 | The analysis of the computed spectra for isomer B is much the same as it was for A.
|
One thing worth noting is that the chemical shifts of the ring-carbons and the methyl carbons seem to have systematically shifted downwards by about 2.7ppm. This is almost certain to be due to the change in symmetry of the molecule - whether it physically changes the chemical shift of the carbon entities, or whether it induces a systematic error in the calculations performed on the molecule in the first place.
IR Spectra - Isomer A
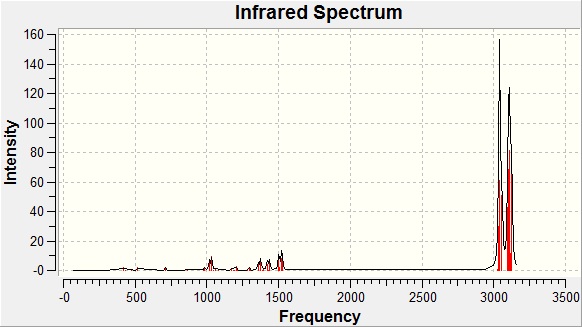 |
As mentioned before, infrared spectroscopy isn't the most useful technique to analyse the products of this reaction since it is essentially a method of detecting functional groups, of which the potential molecules of this reaction have very little. Nonetheless, when forming a computer-generated spectra, it can still be useful to compare to literature to explore the accuracy of the calculations.
A table of key absorption frequencies is below.
| Vibration | Wavenumber / cm-1 (computed)[17] | Wavenumber / cm-1 (reference)[11] |
| Vicinal Hydrogen Wag | 1018 | 1000 |
| Ring Shaking | 1034 | 1016 |
| Vicinal Hydrogen Swing | 1374 | 1141 |
| Methyl press (unison) | 1436 | 1173 |
| Methyl press (opposite) | 1501 | 1316 |
| Methyl bend | 1520 | 1335 |
| Methyl clap | 1525 | 1376 |
| 1392 | ||
| 1455 | ||
| 1470 | ||
| Vicinal hydrogen stretch | 3036 | 2880 |
| Methyl double stretch | 3040 | 2925 |
| Methyl quadruple stretch | 3043 | 2978 |
There is a lot of error involved in calculating the infrared absorption frequencies. This could be because they are calculated in the gas phase where as empirical infrared data is taken with the substance in its standard state at room temperature. This renders it difficult to assign computer generated peaks to those obtained experimentally - however, having said that, to an error of about 50-100 cm-1, peaks occur for the most part in the same regions and to the same intensity.
IR Spectra - Isomer B
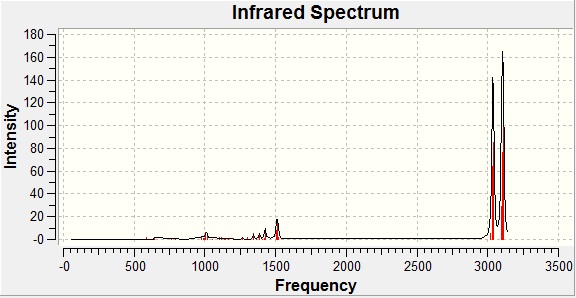 |
| Vibration | Wavenumber / cm-1 (computed)[18] | Wavenumber / cm-1 (reference)[11] |
| Cross-methyl sway | 1006 | 916 |
| Vicinal hydrogen stretch | 1387 | 1382 |
| Methyl press (opposite) | 1426 | 1457 |
| Methyl wag | 1516 | 1465 |
| Methyl stretch (opposite) | 3035 | 2875 |
| Vicinal hydrogen saw | 3042 | 2920 |
| Methyl hydrogen saw | 3105 | 2965 |
Alternative Techniques for Investigating the Products
Spectroscopy isn't the only way to tell the compounds apart. They could be deciphered quite easily from X-Ray crystallography. There is also the possibility that the melting points or boiling points could be recorded - though for this to be a good judge of which isomer has been obtained, the products will have to be separated and purified (which can be cumbersome) and then the melting (or boiling) points recorded at very high accuracy to be able to distinguish between them (and possibly done with repeats to improve accuracy) since similar structures will naturally lead to similar melting points. Comparing obtained melting points to literature will then suggest which product has been obtained.
Melting points:[11]
- Isomer A: 122-122.5oC
- Isomer B: Not given.
Boiling points:[11]
- Isomer A: 128oC
- Isomer B: 109oC
References and Citations
- ↑ 1.0 1.1 A. G. Shultz, L. Flood and J. P. Springer, J. Org. Chemistry, 1986, 51, 838. DOI:10.1021/jo00356a016 Cite error: Invalid
<ref>tag; name "one" defined multiple times with different content - ↑ S. Leleu, C.; Papamicael, F. Marsais, G. Dupas, V.; Levacher, Vincent. Tetrahedron: Asymmetry, 2004, 15, 3919-3928.DOI:10.1016/j.tetasy.2004.11.004
- ↑ Frank S. Fawcett, Chem. Rev., 1950, 47 (2), pp 219–274 DOI:10.1021/cr60147a003
- ↑ 4.0 4.1 Alan B. McEwen, Paul v. R. Schleyer, J. Am. Chem. Soc., 1986, 108 (14), pp 3951–3960 DOI:10.1021/ja00274a016 Cite error: Invalid
<ref>tag; name "four" defined multiple times with different content - ↑ 5.0 5.1 Wilhelm F. Maier, Paul Von Rague Schleyer, J. Am. Chem. Soc., 1981, 103 (8), pp 1891–1900 DOI:10.1021/ja00398a003 Cite error: Invalid
<ref>tag; name "five" defined multiple times with different content - ↑ SPECTRa Chemistry respository, DOI:10042/to-5667
- ↑ SPECTRa Chemistry respository, DOI:10042/to-5669
- ↑ SPECTRa Chemistry respository, DOI:10042/to-5670
- ↑ SPECTRa Chemistry respository, DOI:10042/to-5668
- ↑ Alkanes, Conformational Analysis, Henry Rzepa, date of access: 25/11/2010, http://www.ch.ic.ac.uk/local/organic/conf/c1_alkanes.html
- ↑ 11.0 11.1 11.2 11.3 11.4 11.5 Hideo Yamazaki, Ratimer J. Cvetanovic, J. Am. Chem. Soc., 1969, 91 (2), pp 520–522 DOI:10.1021/ja01030a066 Cite error: Invalid
<ref>tag; name "eight" defined multiple times with different content - ↑ M. Mantina, A. C. Chamberlin, R. Valero, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. A, 2009, 113 (19), pp 5806–5812, DOI:10.1021/jp8111556
- ↑ SPECTRa Chemistry respository, DOI:10042/to-5678
- ↑ Linus Pauling, J. Am. Chem. Soc., 1932, 54 (9), pp 3570–3582, DOI:10.1021/ja01348a011
- ↑ M. S. B. Munson, J. Am. Chem. Soc., 1965, 87 (11), pp 2332–2336, DOI:10.1021/ja01089a005
- ↑ SPECTRa Chemistry respository, DOI:10042/to-5679
- ↑ 17.0 17.1 SPECTRa Chemistry respository, DOI:10042/to-5680
- ↑ 18.0 18.1 SPECTRa Chemistry respository, DOI:10042/to-5681
