Rep:Mod:theoreticalreality

Introduction

This page is the wiki page for James Cronshaw's Third Year Computational Chemistry Lab. This page is for Module 3. Module 2 is here

The Cope Rearrangement

In this section the Cope rearrangement of 1,5-Hexadiene is studied.

Optimization of Products and Reactants

The Cope rearrangement has products and reactants of the same structure (this makes sense as it is a rearrangement) The starting point of this process was to build, on GaussView, a molecule of 1,5-Hexadiene, and change the tortional angles away from any possible minima/maxima. This is so the optimization occurs. Frequency analysis to ensure that a minimum was present, and not a maximum, was also undertaken.

Antiperiplanar Conformer

1,5-Hexadiene app conformer optimization calculation inputs and key results
Calculation type	OPT (optimization)
Method	RHF
Basis Set	3-21G
Final Energy / Hartree	-231.69260
Gradient	0.00001296
Dipole / Deby	0.2021
Point group	C₂
Calculation time	86.8s
Calculation File and type	.log file DOI:10042/22934

The table above details key information about the calculation just undertaken; that it was a Hartree-Fock 'RHF' for singlet molecules (which is what we have). The energy minima and point group match that of conformer anti1 found in Appendix 1 of the instructions.

The item table below that shows a minimum has been found.

 Item               Value     Threshold  Converged?
 Maximum Force            0.000023     0.000450     YES
 RMS     Force            0.000006     0.000300     YES
 Maximum Displacement     0.001121     0.001800     YES
 RMS     Displacement     0.000265     0.001200     YES
 Predicted change in Energy=-1.945290D-08
 Optimization completed.
    -- Stationary point found.

A Jmol of the optimized molecule can be found

Following optimization, frequency analysis of the molecule was undertaken.

1,5-Hexadiene app conformer frequency calculation inputs and key results
Calculation type	OPT (optimization)
Method	RHF
Basis Set	3-21G
Final Energy / Hartree	-231.69260
Gradient	0.00001303
Dipole / Deby	0.2021
Point group	C₂
Calculation time	33.6s
Calculation File and type	.log file DOI:10042/22936

Crucially no negative values of vibration were observed so the system is evidently at a minimum, not a maximum; hence we have a non transient species, and the low frequency table confirms the validity of this calculation and the statement made: The top line shows no large values, and the bottom that none of the large real frequencies are negative (which would mean the molecule is in a transition state)

 Low frequencies ---   -3.3151   -1.6374   -1.3954   -0.0003    0.0007    0.0008
 Low frequencies ---   76.4093   98.3061  109.1042

Gauche Conformer

1,5-Hexadiene gauche conformer optimization calculation inputs and key results
Calculation type	OPT (optimization)
Method	RHF
Basis Set	3-21G
Final Energy / Hartree	-231.69167
Gradient	0.00000548
Dipole / Deby	0.3804
Point group	C₂
Calculation time	96.1s
Calculation File and type	.log file DOI:10042/22940

The energy minima and point group match that of conformer gauche2 found in Appendix 1 of the instructions. The item table below that shows a minimum has been found.

Item               Value     Threshold  Converged?
 Maximum Force            0.000013     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000979     0.001800     YES
 RMS     Displacement     0.000222     0.001200     YES
 Predicted change in Energy=-5.060893D-09
 Optimization completed.
    -- Stationary point found.

A Jmol of the optimized molecule can be found

Following optimization, frequency analysis of the molecule was undertaken.

1,5-Hexadiene app conformer frequency calculation inputs and key results
Calculation type	OPT (optimization)
Method	RHF
Basis Set	3-21G
Final Energy / Hartree	-231.69167
Gradient	0.00000555
Dipole / Deby	0.3804
Point group	C₂
Calculation time	33.6s
Calculation File and type	.log file DOI:10042/22936

Crucially no negative values of vibration were observed so the system is evidently at a minimum, not a maximum; hence we have a non transient species, and the low frequency table confirms the validity of this calculation and the statement made: The top line shows no large values, and the bottom that none of the large real frequencies are negative (which would mean the molecule is in a transition state)

 Low frequencies ---   -1.3177   -0.7342   -0.0004    0.0005    0.0005    1.2287
 Low frequencies ---   63.5642   98.1200  113.3793

Looking for lower energy conformers

From this analysis a key observation is that the Gauche conformer is higher in energy than the antiperiplanar by 0.000093 Hartree (or 0.584kcalmol^-1). It is reasonable to therefore investigate the possibility that the lowest conformation of the molecule would be antiperiplanar.

The first generated structure was an antiperiplanar system, that had higher energy than the previously found anti system. Given this find other possibilities were investigated. Below is a table documenting what was found.

1,5-Hexadiene conformer optimization calculation results
Conformer name (from appendix 1)	Point group	Energy / Hartree	Reference
Anti1	Shape	-231.69260	DOI:10042/22934
Gauche2	C₂	-231.69167	DOI:10042/22940
Anti2	C_i	-231.69254	DOI:10042/22943
Gauche3	C₁	-231.69266	DOI:10042/22944

The table above shows that in fact it is the gauche3 conformer that has the lowest energy, while the anti conformers have higher energies.

Crucially all of these minima matched the provided appendix completely, in symmetry and energy.

Investigating the Anti2 Conformer

Having established the energies of the key low energy conformers of 1,5-Hexadiene, the use of a higher basis set that gives a more accurate description of the molecule follows. This will allow judgment of how good the 3-21G basis set is; if there is a substantial difference in bond angles and length then it clearly is not a great approximation, compared to the 6-31G set. If there is good agreement then the lower, and hence faster basis set can be used for calculations. In the previous section the 3-21G basis set was used.

Optimization with 6-31G

1,5-Hexadiene app2 conformer optimization with 6-31G calculation inputs and key results
Calculation type	OPT (optimization)
Method	RB3LYP
Basis Set	6-31G(d)
Final Energy / Hartree	-234.6117
Gradient	0.00006505
Dipole / Deby	0.00
Point group	C_i
Calculation time	2 min 36.8s
Calculation File and type	.log file DOI:10042/22945

Immediately there are several points of interest from this calculation; first that the point group has not changed (Both are C_i) next the dipole is zero, this is the same for both of them.

The large difference in energy bears no significance whatsoever, by using a different basis set the comparison is no longer valid. What can be compared, however, is bond lengths and angles. Below is a table detailing the two optimized structures.

The convergance of the simulation was confirmed from the .log file:

Item               Value     Threshold  Converged?
 Maximum Force            0.000146     0.000450     YES
 RMS     Force            0.000031     0.000300     YES
 Maximum Displacement     0.001034     0.001800     YES
 RMS     Displacement     0.000407     0.001200     YES
 Predicted change in Energy=-2.181806D-07
 Optimization completed.
    -- Stationary point found.

1,5-Hexadiene app2 conformer optimization with 6-31G calculation inputs and key results
Basis set	C=C bond length / Å	C₃-C₄ bond length / Å	C₂-C₃ bond length / Å	C₂-C₃-C₄ bond angle / degrees	C₁-C₂-C₃ bond angle / degrees
3-21G	1.32	1.55	1.51	111.3	124.8
6-31G(d)	1.33	1.55	1.50	112.6	125.3

It is clear from the above table that the two basis sets have close agreement. The difference in bond lengths and angles are minimal, it is therefore a good enough approximation to use the 3-21G basis set.

Frequency Analysis

Following the optimization, frequency analysis was undertaken of the molecule. This will allow thermochemical data to be obtained.

1,5-Hexadiene app2 conformer frequency inputs and key results
Calculation type	FREQ (frequency)
Method	RB3LYP
Basis Set	6-31G(d)
Final Energy / Hartree	-234.6117
Gradient	0.00007010
Dipole / Deby	0.00
Point group	C_i
Calculation time	3 min 24.2s
Calculation File and type	.log file DOI:10042/22956

The frequency analysis showed no negative frequencies, meaning that the system was at a minimum and not a maximum.

In the thermochemistry section of the .log file the following information was found.

Here all energies are given in Hartree, and are recorded as found in the .log file

Thermochemistry data
Electronic Energy + Zero Point Energy = -234.469202 (at 0K)	E' = E_elec + ZPE
Electronic Energy + Thermal Energy = -234.461855 (at 298.15K, 1atm)	E = E' + E_vib +'E_rot + E_trans
Electronic Enthalpy + Thermal Enthalpy = -234.460911	H = E + RT
Electronic Energy + Thermal Free Energy = -234.500782	G = H - TS

When the simulation is run with an altered temperature of near to zero kelvin there is no correctional values, and all four terms in the above table have the same value; -234.469202.

The difference in consecutive terms could give useful information, such as the value of TS by subtracting G from H, the physical significance of this is, due to the nature of how the model is solved, of no relevance to the real world.

Optimizing a Chair and Boat

In this section the transition state of a process will be investigated. A transition state is a saddle point on a potential energy surface of the first order. It is a maximum and so possesses unique properties such as that it has one imaginary vibrational mode and will have real modes of vibration that lie along the reaction co-ordinate. Having an imaginary frequency is explained due to the relationship between frequency and force constant:

$F r e q u e n c y \propto \frac{1}{2 π} \sqrt{\frac{k}{m}}$

When a system is at a maximum saddle point the force constant becomes negative! Now we have a function that returns the square root of a negative number; an imaginary number.

Optimization of Chair

Allyl Optimization

The first step was to create an allyl fragment, optimize the structure using Hartree-Fock and 3-21G basis set. The results of the optimization are in the table below.

Allyl Optimization inputs and key results
Calculation type	FOPT (Optimization)
Method	UHF
Basis Set	3-21G
Final Energy / Hartree	-115.8230
Gradient	0.00009674
Dipole / Deby	0.0293
Point group	C_2V
Calculation time	20.5s
Calculation File and type	.log file DOI:10042/22967

A Jmol of the optimized molecule can be found

The system was seen to converge from the .log file:

   Item               Value     Threshold  Converged?
 Maximum Force            0.000160     0.000450     YES
 RMS     Force            0.000056     0.000300     YES
 Maximum Displacement     0.000711     0.001800     YES
 RMS     Displacement     0.000290     0.001200     YES
 Predicted change in Energy=-1.860815D-07
 Optimization completed.
    -- Stationary point found.

Hessian Optimization

Having optimized the allyl group, a chair like structure was created by placing two of the allyl groups next to each other, one above the other, out of plane. The gap bewteen terminal carbons was set at approximately 2.2 Angstrom.

Hessian Optimization of Chair inputs and key results
Calculation type	FREQ (Optimization + Frequency)
Method	RHF
Basis Set	3-21G
Final Energy / Hartree	-231.6193
Gradient	0.00000692
Dipole / Deby	0.00
Point group	C_2h
Calculation time	35.4s
Calculation File and type	.log file DOI:10042/22971

A Jmol of the optimized molecule can be found

The system was seen to converge from the .log file:

  Item               Value     Threshold  Converged?
 Maximum Force            0.000012     0.000450     YES
 RMS     Force            0.000002     0.000300     YES
 Maximum Displacement     0.000313     0.001800     YES
 RMS     Displacement     0.000060     0.001200     YES
 Predicted change in Energy=-8.025162D-09
 Optimization completed.
    -- Stationary point found.

The frequency analysis showed one negative frequency at -818cm^-1 this vibration is shown below. It is clearly the Cope rearrangement!

Frozen Coordinate Optimization

The Input file for the Hessian Optimization was reopened and edited to allow a frozen coordinate calculation to be carried out. This process requires the minimization of the structure in all but one way (here the distance between the two allyl groups) before finding the transition state. The results below are for the final structure after the freezing of coordinates, and minimization had been carried out, as well as the transition state being found.

Frozen Coordinate Optimization of Chair inputs and key results
Calculation type	FREQ (Optimization + Frequency)
Method	RHF
Basis Set	3-21G
Final Energy / Hartree	-231.6193
Gradient	0.00005152
Dipole / Deby	0.00
Point group	C_2h
Calculation time	35.6s
Calculation File and type	.log file DOI:10042/22970

A Jmol of the optimized molecule can be found

The system was seen to converge from the .log file:

   Item               Value     Threshold  Converged?
 Maximum Force            0.000026     0.000450     YES
 RMS     Force            0.000008     0.000300     YES
 Maximum Displacement     0.001051     0.001800     YES
 RMS     Displacement     0.000167     0.001200     YES
 Predicted change in Energy=-2.500466D-07
 Optimization completed.
    -- Stationary point found.

The frequency analysis showed one negative frequency at -818cm^-1 this vibration is shown below, and is the same frequency as the Hessian Method. It is of course clearly the Cope rearrangement!

Comparison of Hessian and Frozen Methods

In this section the two methods will be compared to see if any differences exist between two routes to what should be the same solution. In other words do both methods yield the same outcome?

Comparison of Hessian and Frozen Coordinate results
Calculation type	Energy / Hartree	Allyl - Allyl distance / Å	Angle of Allyl C-C-C / degrees	Imaginary vibration wavenumber / cm^-1
Hessian	-231.6193	2.02	120.5	818
Frozen	-231.6193	2.02	120.5	818

There is clearly no discernible difference whatsoever with these two methods.

Optimization of a Boat

In this section a boat transition structure is studied.

The QST2 method

The method was attempted twice, once without altering the geometry of the reactants and products that are the anti2 conformer of 1,5-hexadiene, and once with altered bond angles, and dihedral angles. The first attemt was without any structural alterations to the optimized structures, but with a renumbering of the atoms to a specified guide, such that the products and reactants were those of the cope rearrangement.

QST2 Optimization of 1,5-hexadiene transition state inputs and key results
Calculation type	FREQ (Optimization + Frequency)
Method	RHF
Basis Set	3-21G
Final Energy / Hartree	-231.6193
Gradient	0.00002073
Dipole / Deby	0.00
Point group	C_2h
Calculation time	34.9s
Calculation File and type	.log file DOI:10042/22977

A Jmol of the chair can be found

The system did converge as required as the item table below shows.

Item               Value     Threshold  Converged?
 Maximum Force            0.000050     0.000450     YES
 RMS     Force            0.000017     0.000300     YES
 Maximum Displacement     0.001339     0.001800     YES
 RMS     Displacement     0.000354     0.001200     YES
 Predicted change in Energy=-8.900799D-08
 Optimization completed.
    -- Stationary point found.

The structure formed is that of a Chair and not of a Boat, the calculation has thus not succeeded in what we wanted to achieve, although it is important to note that it has found a vaid transition state! The chair found is identical to that found in previous sections, with the same 818cm^-1 imaginary stretch showing the cope rearrangement. This makes sense as the programme simply found the first transition state, as this is what is was asked to do in the method.

A second QST2 calculation

Having failed to find the desired boat transition state on the first attempt, several key alterations were made; these were designed to ensure that the nearest and first transition state that the calculation would encounter would be is the boat conformer. The changes made were to set the middle C₃-C₄ dihedral angle to zero, and the interior angles of the C₂-C₃-C₄ and C₃-C₄-C₅ groups to 100 degrees. (Numbering of Carbons where 1 and 6 are terminal, and progression is linear)

QST2 Optimization of 1,5-hexadiene transition state inputs and key results
Calculation type	FREQ (Optimization + Frequency)
Method	RHF
Basis Set	3-21G
Final Energy / Hartree	-231.6028
Gradient	0.00002904
Dipole / Deby	0.158
Point group	C_2v
Calculation time	34.7s
Calculation File and type	.log file DOI:10042/22980

This calculation did find the boat conformer and calculated the properties that it has. These are compared with that of the chair below.

A Jmol of the chair can be found

The calcualtion found a stationary point as required for a valid calculation:

         Item               Value     Threshold  Converged?
 Maximum Force            0.000057     0.000450     YES
 RMS     Force            0.000014     0.000300     YES
 Maximum Displacement     0.000738     0.001800     YES
 RMS     Displacement     0.000228     0.001200     YES
 Predicted change in Energy= 1.054633D-08
 Optimization completed.
    -- Stationary point found.

From frequency analysis a single imaginary frequency at 841cm^-1 that had the appearance of a cope rearrangement progressing via the boat conformer. This is seen below.

Comparison of Boat and Chair conformers

Having now calculated both transition states possible in the rearrangement, this section will give a brief overview of them side by side with comment.

QST2 Optimization of 1,5-hexadiene transition state inputs and key results
Transition State	Energy / Hartree	Imaginary vibration wavenumber / cm^-1	Dipole / Deby
Chair	-231.6193	-818	0.00
Boat	-231.6028	-841	0.158

From the comparison there are several key differences; first is the energy difference. The chair conformer has a lower energy by 0.0165 Hartree, or 10.4kcalmol^-1. This is not an inconsiderable amount of energy. The lower energy of transition is accompanied by a lower frequency of imaginary vibration. Finally the less symmetric shape of the boat arrangement results in an overall dipole, while for the chair there is no dipole. So, unlike the initial and final conformers, the lower energy systems are less symmetric.

Another interesting result from this is the calculations predict that the faster rate of rearrangement will be via chair not boat. The chair is also, in having the lowest transition energy, the lowest energy path, and as such it is this transition stat that the Intrinsic Reaction Coordinate computation should be carried out on.

IRC Calculations

The IRC, or Intrinsic Reaction Coordinate is the minimum energy path that the process can pass through. It can be used to determine which product / reactants are linked as well as investigating a range of reaction properties from order to rate.

Chair IRC

Initially the lowest energy transition state, the chair, was considered for IRC calculation. The results of an IRC calculation are shown below. This is followed by discussion. The chair generated from the frozen coordinate method was used as a base line.

IRC calculation inputs and key results. NOTE: Values are for last step.
Calculation type	IRC
Method	RHF
Basis Set	3-21G
Final Energy / Hartree	-231.6916
Gradient	0.00015228
Dipole / Deby	0.3630
Calculation time	17mins 26.5s
Calculation File and type	.log file DOI:10042/22999

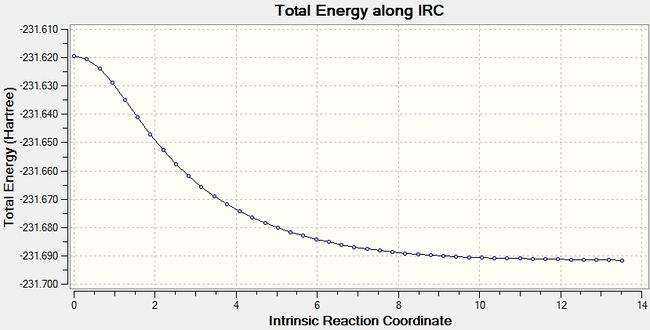
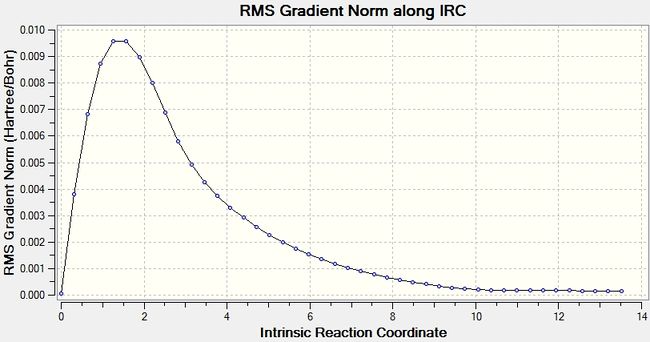
The above data is for only one point. In order to show all of the calculated data, the IRC can be shown in two graph: one is a graph of total energy, the other of gradient, both plotted against reaction coordinate. The energy graph should, for an optimized molecule, tend to a value equivalent to one of the optimized 1,5-hexadiene structures, and the gradient tend to zero as a minimum is found. These two graphs are shown below.

The total energy graph show that the system does tend to a minimum, however it has not quite reached it, with the final point dropping; if it was a minimum then it would be flat. The energy of this is, as stated above, -231.6916 Hartree, compared with a minimum of -231.69266 for the minimum conformer of 1,5-hexadiene. Indeed the molecule is close to the gauche2 structure. A further optimization may therefore be warrented. The Root mean squared of the gradient will aid in deciding whether this is needed.

The gradient graph shows a decline tending to zero, with a minimum of 0.00015228. This is much higher than the gradient could be, and shows that there is some minimization still to be achieved.

Optimization of the molecule

There are two ways to find the minimum, one is to increase the number of points in the IRC, and the other is simply to perform an optimization on the final structure. The former requires the entire calculation to be repeated, while the latter does not. Given the long length of IRC calculations the optimization was chosen as an initial approach as the molecule is close to a minimum. This was a successful technique in showing that the system was indeed tending to the gauche2 conformer which it was close to before.

Optimization calculation key inputs and results.
Calculation type	OPT (Optimization)
Method	RHF
Basis Set	3-21G
Final Energy / Hartree	-231.6917
Gradient	0.00000475
Dipole / Deby	0.3806
Point group	C₂
Calculation time	48.6s
Calculation File and type	.log file DOI:10042/23005

The optimization has thus show the Cope rearrangement has seen an anti2 conformer go to a gauche2 conformer. Neither of these are the minimum possible, but crucially are localized minima. The gauche3 conformer that is the overall minimum should be able to be reached, given it was not reached from the chair transition state it is theorized that the boat transition state would lead to the gauche3 transition state.

Reoptimization of Chair and Boat

In order to calculate the activation energies of both the boat and chair the two structures will be optimized to a higher basis set of 6-31G. As stated earlier the 3-21G is a reasonably good basis set, however it isn't as good as the higher 6-31G so for energetic comparisons of structures the higher basis set makes sense.

Chair Optimization

Optimization of Chair with 6-31G calculation key inputs and results.
Calculation type	OPT (Optimization)
Method	RB3LYP
Basis Set	6-31G(d)
Final Energy / Hartree	-234.556983
Gradient	0.00001224
Dipole / Deby	0.00
Point group	C_2h
Calculation time	6min 15.0s
Calculation File and type	.log file here

The calculation converged, as shown by the item table.

  Item               Value     Threshold  Converged?
 Maximum Force            0.000026     0.000450     YES
 RMS     Force            0.000005     0.000300     YES
 Maximum Displacement     0.000106     0.001800     YES
 RMS     Displacement     0.000035     0.001200     YES
 Predicted change in Energy=-5.100383D-09
 Optimization completed.
    -- Stationary point found.

The energy of the chair was . This can be compared to boat and initial structures of the same method and basis set.

Boat Optimization

Optimization of Boat with 6-31G calculation key inputs and results.
Calculation type	OPT (Optimization)
Method	RB3LYP
Basis Set	6-31G(d)
Final Energy / Hartree	-234.543093
Gradient	0.00000026
Dipole / Deby	0.0613
Point group	C_2v
Calculation time	2min 58.0s
Calculation File and type	.log file here

The calculation converged, as shown by the item table.

Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000019     0.001800     YES
 RMS     Displacement     0.000005     0.001200     YES
 Predicted change in Energy=-3.027564D-11
 Optimization completed.
    -- Stationary point found.

Table of comparison

The key data is the energy, which can be compared for like basis sets and method for the Boat, the Chair, and the initial structure of the reaction; anti2 1,5-Hexadiene energy. These are done in the table below with an experimental comparison.

Method/Basis set	HF/3-21G			B3LYP/6-31G(d)
	Electronic energy	Sum of electronic and zero-point energies at 0K	Sum of electronic and thermal energies at 298.15K	Electronic energy	Sum of electronic and zero-point energies at 0K	Sum of electronic and thermal energies at 298.15K
Chair TS	-231.619322	-231.466705	-231.461346	-234.556983	-234.414929	-234.409008
Boat TS	-231.602803	-231.450929	-231.445301	-234.543093	-234.402342	-234.396007
Reactant (anti2)	-231.692535	-231.539540	-231.532566	-234.611710	-234.469202	-234.461855

From this information we can find the activation energies for each method and transition state by taking the difference in energy from reactant to transition state. These are shown next to the experimental values provided in the script in the table below.

Activation energies, all energies are quoted in kcalmol^-1
Transition state	HF/3-21G 0K	HF/3-21G 298.15K	B3LYP/6-31G 0K	B3LYP/6-31G 298.15K	Experimental
Chair	45.70	44.69	34.06	33.16	33.5 ±0.5
Boat	55.60	54.76	41.96	41.32	44.7 ±2.0

This data shows that the difference between the Hartree-Fock and DFD is substantial in energies despite the near identical geometries. Additionally the agreement between experimental and calculated results is reasonably good, with both conformers agreeing qualitatively with the experimental that the chair is a lower energy path, and the chair in particular showed strong agreement with experimental figures. The boat was a little further off the experimental data.

The Diels-Alder Cycloaddition

The reaction between a diene and dieneophile is one of the most investigated cycloadditions there is. It is arguably the quintessential pericyclic reaction and is known as the Diels-Alder. In this section this reaction will be investigated, both as a simple unsubstituted process and with reactants bound in rings. The former to study the nature of the reaction path, and the latter the regioselectivity of the reaction.

Butadiene and Ethene

The simplest Diels-Alder is the reaction between butadiene and ethene to form cyclohexene. The principles of the reaction are the same here as for any other; a [4+2] cycloaddition involving the pi electrons delocalized in the the diene and electrons in the dieneophile's pi bond. The process is HOMO/LUMO governed. The process to understand the process will require optimization of reactants, the finding of the transition structure with accompanying frequency and MO calculations to build discussion on.

Optimization of Cis-Butadiene

Optimization and Frequency calculation of Butadiene key inputs and results.
Calculation type	FREQ (Opt+Freq)
Method	RAM1
Basis Set	ZDO
Final Energy / Hartree	0.04878534
Gradient	0.00000300
Dipole / Deby	0.0354
Point group	C₂
Calculation time	4.5s
Calculation File and type	.log file DOI:10042/23041

The calculation .log file showed that there was convergence

Item               Value     Threshold  Converged?
 Maximum Force            0.000005     0.000450     YES
 RMS     Force            0.000002     0.000300     YES
 Maximum Displacement     0.000733     0.001800     YES
 RMS     Displacement     0.000259     0.001200     YES
 Predicted change in Energy=-8.605054D-10
 Optimization completed.
    -- Stationary point found.

In addition the frequency calculation showed all positive values for the 24 modes. The optimized structure can be found as a Jmol . Note that it isn't planer, despite being close.

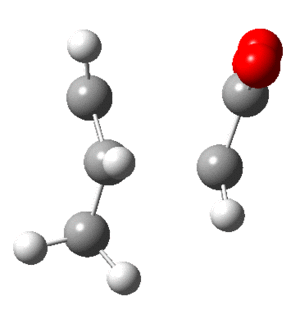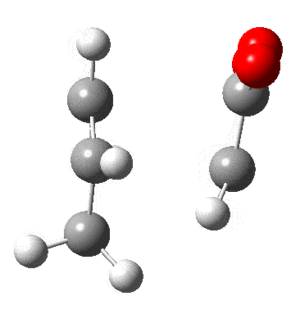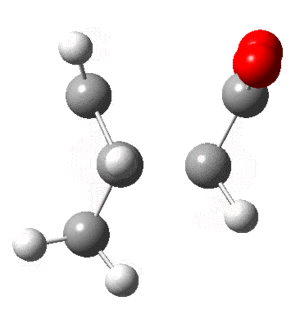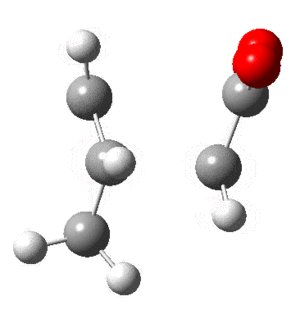
MO of cis-Butadiene

The checkpoint file was opened and molecular orbitals calculated for the HOMO/LUMO region; p orbital interactions only. These are shown below. The images are shown with the highest energy molecular orbital furthest up the page.

LUMO +1 Three nodes; Antisymmetric

LUMO Two nodes; Symmetric

HOMO One node; Antisymmetric

HOMO -1 No nodes; Symmetric

Optimization of Ethene

Optimization and Frequency calculation of Ethene key inputs and results.
Calculation type	FREQ (Opt+Freq)
Method	RAM1
Basis Set	ZDO
Final Energy / Hartree	0.02619024
Gradient	0.00000945
Dipole / Deby	0.00
Point group	D_2h
Calculation time	7.2s
Calculation File and type	.log file DOI:10042/23061

Ethene MO visualization

Using the checkpoint file the molecular orbitals around the HOMO LUMO region were found. These are shown below. The highest energy orbital, the lumo, is furthest up the page.

LUMO one node; Antisymmetric

HOMO no nodes; Symmetric

Comparison of MOs

In this section the molecular orbitals of ethene and butadiene. The orbitals can interact favorably when both of them are either symmetric or antisymmetric. The table below shows that the result of this is the HOMO of one and LUMO of the other interact favorably.

Optimization and Frequency calculation of Ethene key inputs and results.
Molecule	HOMO	LUMO
Butadiene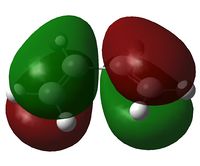
Ethene

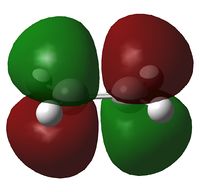
A Diels Alder Transition State

In this section the transition state of butadiene and ethene reacting in a cycloaddition is understood.

Optimization

The method to achieve this was to draw a bicycle with eight carbon atoms, remove two then break the bonds from another pair to the rest of the ring before finally removing two Hydrogens and adding double bonds as required. The result of this was to provide the system with a good guess of the transition structure. In order to improve it further the sharp angle between fragments was reduced by lowering the ethene closer to the butadiene, and moving it further away in the plane of butadiene.

Transition structure optimization key inputs and results.
Calculation type	FREQ (Opt+Freq)
Method	RAM1
Basis Set	ZDO
Final Energy / Hartree	0.111655
Gradient	0.00002029
Dipole / Deby	0.560
Point group	C_S
Calculation time	9.0s
Calculation File and type	.log file here

The calculation converged as the .log file showed in the item table:

         Item               Value     Threshold  Converged?
 Maximum Force            0.000045     0.000450     YES
 RMS     Force            0.000010     0.000300     YES
 Maximum Displacement     0.001104     0.001800     YES
 RMS     Displacement     0.000300     0.001200     YES
 Predicted change in Energy=-4.027167D-08
 Optimization completed.
    -- Stationary point found.

On viewing the vibrational analysis one negative frequency was seen (implying imaginary) showing that a transition state had been found. This was at -956cm^-1 and is clearly the motion of a diels-alder reaction. Key features are the forming bond that is dashed on the butadiene where the double bond will eventually form as well as the deflection of Hydrogens. By this what is meant is that the Hydrogen atoms that had been planar initially are now bent; where the new single bonds are to be formed they bend down, away from the incoming butene, while those where the double bond is forming are planar. This can clearly be seen in the animation of this key vibration that is shown below from above and the side.

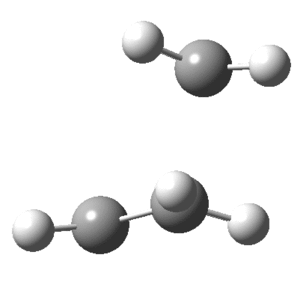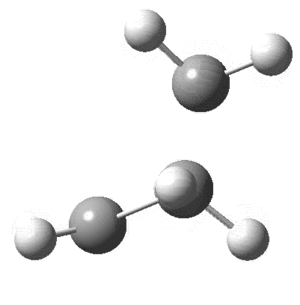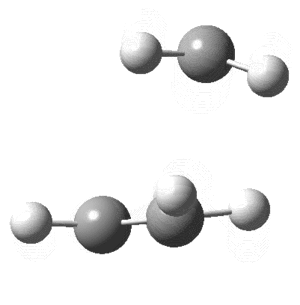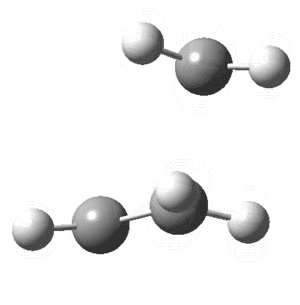
Transition state of Butadiene and Ethene undergoing a Diels-Alder reaction.

The vibration above shows the bond stretching of double bonds, and simultaneous shortening of the double bond forming. The now optimized transition structure can now be analyzed from an MO perspective.

Molecular Orbitals

The key region of MOs is the HOMO-LUMO region; specifically The HOMO. By comparing this to the same region of the two fragments, butadiene and ethene, found earlier the orbital approximation made in the Woodward-Hoffmann rules. The prediction that these rules make can be shown using a build up of p orbitals on a skeleton of the structure. Below is the predicted structure and the calculated HOMO molecular orbital are shown side by side. Notice how similar they both are.

File:CRON Woodman prediction.pdf

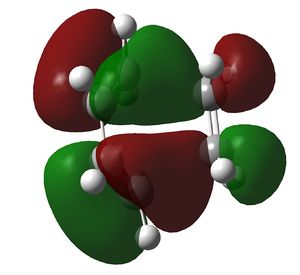
Both structures have nodes at all atoms. The similarity is almost uncanny, and the calculated picture is clear evidence of the Woodward-Hoffmann model being correct.

Why the Reaction Occurs

The reaction is best understood as to why it occurs by the interaction between the HOMO of butadiene and LUMO of ethene. The image below shows all three orbitals with the key symmetry plane drawn on. The interaction between two antisymmetric orbitals yields another antisymmetric orbital. This agrees with MO theory; two groups of the same symmetry yielding another with the same symmetry.

File:CRON Diels alder homo.pdf

Geometry of Transition State

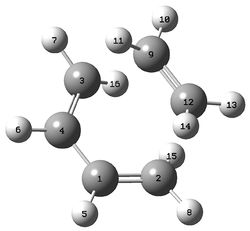
The image below is of the diels-alder transition state labeled in order to aid the description of the geometry.

Group	C₁-C₂	C₁-C₄	C₉-C₁₂	C₂-C₁₂
Bond length / Angstrom	1.38	1.40	1.38	2.11

Note that while the C₂-C₁₂ distance is not a true bond, it is important in as much as it shows the progress to a new bond being formed.

If these distances are compared to a typical C-C bonds and interesting discovery is made. A typical sp³-sp³ hybrid distance is 1.524Å^[1], while a typical sp²-sp² hybrid distance is 1.455Å^[1] in a conjugated system. Compared to both of these the bonds measured are all shorter by some margin, and very close in distance given that the supposedly single bond is just 0.02Å longer than the others. By looking at the bond length of C-C aromatic literacture value of 1.380Å^[1] it is clear that what we have in the transition state is closer to an aromatic molecule than single and double bonds. It is this aromaticity that is key in reducing the energy of the transition state and hence allowing the reaction to happen.

Cyclohexa-1,3-diene and Maleic Anhydride Diels-Alder

Here the products of Cyclohexa-1,3-diene and Maleic Anhydride will be investigeted by looking at the two transition states that they go through. The initial step is to optimize the exo and endo product.

Optimization of Exo Product

Optimization key inputs and results.
Calculation type	FREQ (Opt+Freq)
Method	RAM1
Basis Set	ZDO
Final Energy / Hartree	-0.159909
Gradient	0.00007790
Dipole / Deby	5.26
Point group	C_S
Calculation time	10.7s
Calculation File and type	.log file DOI:10042/23146

The optimized molecule can be found

The calculation converged as the .log file showed in the item table:

         Item               Value     Threshold  Converged?
 Maximum Force            0.000252     0.000450     YES
 RMS     Force            0.000038     0.000300     YES
 Maximum Displacement     0.000855     0.001800     YES
 RMS     Displacement     0.000236     0.001200     YES
 Predicted change in Energy=-2.971599D-07
 Optimization completed.
    -- Stationary point found.

Optimization of Endo Product

Optimization key inputs and results.
Calculation type	FREQ (Opt+Freq)
Method	RAM1
Basis Set	ZDO
Final Energy / Hartree	-0.160170
Gradient	0.00007790
Dipole / Deby	5.58
Point group	C_S
Calculation time	10.7s
Calculation File and type	.log file DOI:10042/23150

The optimized molecule can be found

The calculation converged as the .log file showed in the item table:

         Item               Value     Threshold  Converged?
 Maximum Force            0.000274     0.000450     YES
 RMS     Force            0.000035     0.000300     YES
 Maximum Displacement     0.001651     0.001800     YES
 RMS     Displacement     0.000299     0.001200     YES
 Predicted change in Energy=-4.840113D-07
 Optimization completed.
    -- Stationary point found.

Structural Comparison

The two optimizations show that the Endo product is indeed the lower in energy of the two products. THe endo product was lower by 0.164kcalmol^-1. This is a small difference in energy when compared to earlier calculations. The favoring of the endo product would be in the order of hundreds, not sufficient to explain why it is so favored. Furthermore if the reaction is kinetically controlled the final energy of the products should not matter, what does matter is the relative energies of the transition states. In order to find this out the transition states must now be found.

Exo transition state

In order to find the exo transition state a simple method of removing the C-C bonds formed from the product and increase the distance of the two groups to 2.2angstrom. Following this a TS (Berny) Optimization and Frequency calculation to find a maximum was undertaken. The result of this is in more detail below.

Optimization key inputs and results.
Calculation type	FREQ (Opt+Freq)
Method	RAM1
Basis Set	ZDO
Final Energy / Hartree	-0.0504198
Gradient	0.00001067
Dipole / Deby	5.56
Point group	C_S
Calculation time	8.0s
Calculation File and type	.log file here

The .log file was consulted to check that convergence had occurred. The result is shown below.

         Item               Value     Threshold  Converged?
 Maximum Force            0.000037     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000700     0.001800     YES
 RMS     Displacement     0.000138     0.001200     YES
 Predicted change in Energy=-9.987730D-09
 Optimization completed.
    -- Stationary point found.

The Frequency analysis revealed a single negative frequency at -812cm^-1. This was, when visualized, the diels alder reaction path! The result of this is that there is clear evidence that this is the transition state that has been found and that the process for this is, as for the butadiene/ethene reaction a concerted reaction going via an aromatic transition state. The imaginary vibration is shown below from the side and above. The bonds are conjugated as chem draw shows with the dashed lines.

Endo transition state

In order to find the endo transition state a simple method of removing the C-C bonds formed from the product and increase the distance of the two groups to 2.2angstrom. Following this a TS (Berny) Optimization and Frequency calculation to find a maximum was undertaken. The result of this is in more detail below.

Optimization key inputs and results.
Calculation type	FREQ (Opt+Freq)
Method	RAM1
Basis Set	ZDO
Final Energy / Hartree	-0.0515048
Gradient	0.00000456
Dipole / Deby	6.67
Point group	C_S
Calculation time	11.0s
Calculation File and type	.log file DOI:10042/23192

The .log file was consulted to check that convergence had occurred. The result is shown below.

         Item               Value     Threshold  Converged?
 Maximum Force            0.000016     0.000450     YES
 RMS     Force            0.000002     0.000300     YES
 Maximum Displacement     0.000216     0.001800     YES
 RMS     Displacement     0.000055     0.001200     YES
 Predicted change in Energy=-1.506453D-09
 Optimization completed.
    -- Stationary point found.

The Frequency analysis revealed a single negative frequency at -806cm^-1. This was, when visualized, the diels alder reaction path! The result of this is that there is clear evidence that this is the transition state that has been found and that the process for this is, as for the butadiene/ethene reaction a concerted reaction going via an aromatic transition state. The imaginary vibration is shown below from the side and above. Note the above view shows a shortening bond where the double bond will form and lengthening where the singles will. The bonds are conjugated as chem draw shows with the dashed lines.

Comparison of Energies

Previously the energies of the exo and endo product were compared and shown to be very close (endo is lower by 0.164kcalmol^-1). Now having found the transition states the energies of these transient species can be compared. The endo species was lower in energy by 0.394kcalmol^-1. This is much larger than the energy difference in products showning that the determining factor in these reactions is the height of the energy barrier. Of course under kinetic control the reaction is always determined by this.

The importance of the lower energy endo is it is favored as a product. So why is it lower in energy? There are two competing explanation: Steric and Orbital based. Here the former will be put forward, and in the following section the other argument will be made.

Reason explained sterically: The two images below show this clearly. The black arrow shows the Carbon Hydrogen distance between the two groups forming the product. The crucial element is that on the left the endo product has the maleic anhydride aligned such that it is closest to the double bond with a distance of 3.0Angstroms^[1], while the exo product has not got the benefit of the reduced number of hydrogens due to the single bond. The exo product distance over the black line is 2.4Angstroms. Given the sum of Carbon and Hydrogen's Van der Waal radii is 2.9Angstrom this shows that with the endo product there is no interaction, while the exo will experience a repulsive interaction as the two groups are too close.

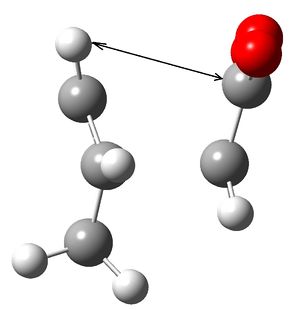Left: Endo product Left: Exo product

Comparision of Molecular Orbitals

In this section the molecular orbitals of the two transition states are examined. As has already been stated the process is such that the product is of little relevance due to the kinetic barrier. The transition state HOMO's are shown below. They are remarkably similar, in fact they are as good as indistinguishable. Given this they have been shown from opposite angles to aid in visualization.

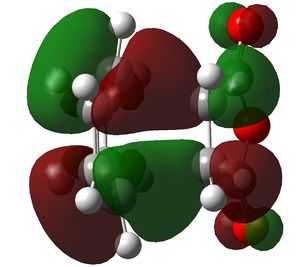Left: Exo ts homo 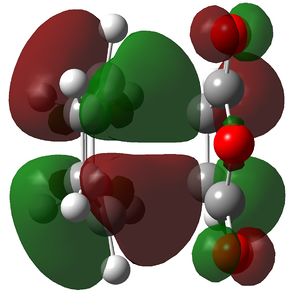Left: Endo ts homo

While the two structures may be very similar they both show interesting features. Comparing with the diels alder transisition state of butadiene and ethene there are extensive similarities in as much as an antisymmetric product has formed and it is thus from the HOMO of the diene and LUMO of the dieneophile.

Secondary Orbital Overlap effects explaining the energy difference.

The secondary orbital overlap effect is simply the positive overlap of a non-active frame in the frontier molecular orbitals of a pericyclic reaction. We see this occur here as exemplified by the oxygen p orbitals interacting favorably to aid the orbital construction, however it is no more so for one or the other of the two transition states.

So the steric factor as explained previously determines the selectivity of the endo group. This conclusion is corroborated by prior reserch in the same field using an identical semi-empirical basis set. The key is in steric effects not the orbitals.^[2]

Extention

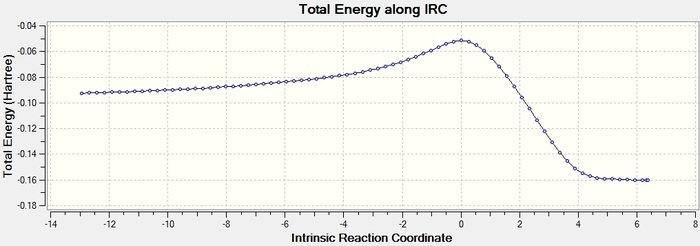
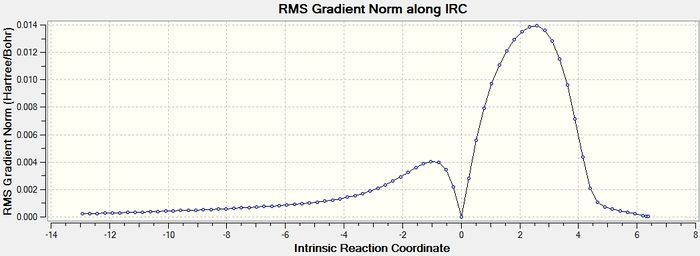
This section is an extention of the original project's remit. It it the endo side of the reaction discussed in the preceding section will be investigated further using an IRC calculation. The aim of undertaking this research is to provide an overview of the diels alder reaction of cylcohexa-1,3-diene and maleic anhydride, showing reaction order as an inference of the reaction co-ordinate graph generated, as well as the relative energies of starting material and product.

The IRC calculation was undertaken with a resulting 77 steps from reactant to product via a single transition state.

IRC key inputs and results.
Calculation type	FREQ (Opt+Freq)
Method	RAM1
Basis Set	ZDO
Gradient of reactant	0.00022374
Gradient of product	0.00003743
Dipole / Deby	6.67
Calculation time	8min 46.0s
Calculation File and type	.log file here

The result of the IRC calculation has at either side of the calculation path gradients that are low enough that the structures are evidently optimized. The graph of IRC against energy and IRC against gradient is precisely what would be expected for a concerted pericyclic addition. Other information that these graphs show is from the energy graph that the process is exothermic. The two graphs are shown below.

The Energy/IRC graph

So the IRC shows that the simulation suggestst that the endo product is not in fact from an endothermic reaction, but an exothermic process. Of course the basis set is only semi-empirical.

References

↑ ^1.0 ^1.1 ^1.2 ^1.3 CRC Handbook 93^rd Edition
↑ Marye Anne Fox , Raul Cardona , Nicoline J. Kiwiet J. Org. Chem., 1987, 52 (8), pp 1469–1474DOI:10.1021/jo00384a016

[CRC-1] 1.0 ^1.1 ^1.2 ^1.3 CRC Handbook 93^rd Edition

[2] Marye Anne Fox , Raul Cardona , Nicoline J. Kiwiet J. Org. Chem., 1987, 52 (8), pp 1469–1474DOI:10.1021/jo00384a016

[1]

[2]