Rep:Mod:thatssoraven

S. Stow - Computational Chemistry

for the DFT mini project please click here

1. The Hydrogenation of Cyclopentadiene Dimer

Introduction

The conformations of molecules can be optimised and properties calculated in various ways using a variety of computational techniques, ranging from wholly empirical to ab inition quantum mechanical treatments. Using calculated energies the hypothetical populations of two isomers can be calculated using the boltzmann distribution from their relative energies. Molecular orbitals can be calculated to varying degrees and used to simulate NMR and IR spectra, and to qualitatively assess bonding contributions.

A. Cyclopentadiene Conformation

Cyclopentadiene readily undergoes a Diels-Alder [4+2] Cycloaddition reaction forming the cyclopentadiene dimers '1' & '2'. This reaction is useful in synthesis as a starting point for bridged ring systems because it reliably forms two stereocenters and has double bonds which can be functionalised. In this section the preferred conformation of the cyclopentadiene dimer is investigated, and the hydrogenation rates of the endo products investigated.

Cyclopentadiene dimers 1 & 2 were modelled using simple Molecular mechanics calculations (mm2) with ChemBio3d . '1' is the Exo product formed when the two cyclopentadiene rings lie away from each other before they react. '2' is the Endo product, formed when the two rings lie over each other before they react. The information produced by the MM2 method is relative and appropriate for assessing relative energies between isomeric compounds.

cyclopentane dimers 1:EXO, 2:ENDO

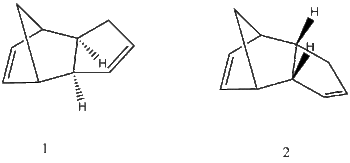
                        1: EXO /kcalmol-1      2:ENDO /kcalmol-1
 Stretch                1.2858                  1.2506  
 Bend:                  20.5791                 20.8478
 Stretch-Bend:          -0.8381                 -0.8358
 Torsion:                7.6571                 9.5109
 Non-1,4 VDW:           -1.4171                 -1.5430
 1,4 VDW:                4.2322                 4.3194
 Dipole/Dipole:          0.3776                 0.4476
 Total Energy:           31.8766                33.9975

Using the Boltzmann distribution the populations of 1 and 2 (for the hypothetical thermodynamically controlled reaction) are 89% EXO.

The MM2 calculation indicates that the endo configuration is of higher energy than the exo configuration. In reality the formation of the dimer is selective for the Endo form. The Endo form '2' is the kinetic product of the reaction, formed because of the favourable pi-stacking interaction between the two cyclopentadiene pi systems. the Exo product is formed when the two pi systems don't stack before reacting, which would be a higher energy transition state. This indicates the Endo kinetic product has a more reactant-like transition state and the Exo product has a more product-like transition state.

B. Hydrogenation Product

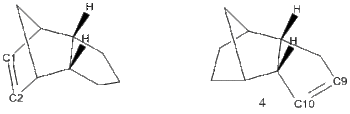
The endo product (2) can be hydrogenated, giving a monohydrogenated product. Which double bond is hydrogenated can be assessed with calculation of the relative energies of the two possible hydrogenation products. The hydrogenation itself is hypothetical, and steric hindrances to the hydrogenation mechanism aren't considered.

(3) - Hydrogenated at unbridged ring double bond

hydrogenated endo dimers

                        Product (3)/kcalmol-1     Product (4)/kcalmol-1   
 Stretch:                1.2775                     1.0968
 Bend:                   19.8565                    14.5206
 Stretch-Bend:          -0.8346                    -0.5495
 Torsion:                10.8110                    12.4984
 Non-1,4 VDW:           -1.2202                    -1.0670
 1,4 VDW:                5.6328                     4.5121
 Dipole/Dipole:          0.1621                     0.1406
 Total Energy:           35.6850                    31.1521

Comparison of the relative energies of (3) and (4) indicates that hydrogenation at the bridged ring site C1=C2 is favourable thermodynamically, due largely to a decrease in bending strain and a decrease in Torsion. To analyse which bonds were responsible for the most bond strain and torsion in the products all the bond angles and dihedral angles were measured and compared to the 'ideal values' for those bonds, which are used by the MM2 method to assess energy contributions.

the populations of the two products: 98.9% [4] to 1.1% [3].

for (3) the double bond at C1=C2 is considerably more strained than the double bond at C9=C10 for molecule (4). The MM2 program assigns the angle C=C-C an ideal value of 122^o. for (3) both bond angles are 107.77^o, a deviation of 14.3^o. For (4) the bond angles are 112.4^o for C10 and 113^o for C9, a deviation of only 9.5^o and 9^o. The Bridgehead carbon was almost equally strained in both molecules, with a bond angle of 93.7^o for (3),surprisingly marginally less strained than (4)which had 92.6^o deviating from the ideal of 109.5^o by 16.9^o. For (3) all the carbons C1 through C5 deviated by at least 10^o.

the other paramaters are broadly similar, with a slight increase in torsion for (4) due to a twist in the ring caused by the double bond - Because the double bond is not in a symmetrical position.

Based on this analysis, The expected thermodynamic hydrogenation product is (4), because it releases 5.5kcalmol^-1 more of strain from the bridged ring than does the hydrogenation of the other double bond. Whilst this might be a reasonable prediction for a dissolving metal reduction, where the reduction is thermodynamically controlled, under conditions such as Pd/C + H2 this wouldn't be the case because the bridgehead carbon would likely hinder access to the C1-2 double bond, whereas access to the C9-10 alkene is good.

2. Stereochemistry and reactivity of an intermediate in the synthesis of Taxol

The two conformers of the taxol intermediate

1: 'UP'	2: 'DOWN'
Taxol intermediate 1 'UP'	Taxol intermediate 2 'DOWN'

A. Carbonyl Conformation

 Isomer:                'Up' (9)       'Down'(10)   
Stretch:                2.7844          2.6202
Bend:                   16.5381         11.3388
Stretch-Bend:           0.4298          0.3430
Torsion:                18.2575         19.6718
Non-1,4 VDW:           -1.5553         -2.1616 
1,4 VDW:                13.1098         12.8727
Dipole/Dipole:         -1.7248         -2.0021
Total Energy:           47.8396         42.6829

The 'Down' Isomer has lower energy by 5.15kca, due largely to a 5.2kca difference in the bending energy of the molecule caused by more optimal bond angles. there were also slight contributions from slightly improved Van-der-Waals interactions and dipole interactions in the down isomer, although bond torsion was slightly less favourable.

the relative populations based on the energy differences are 99.47% 'Down' to 0.52% 'Up' at equilibrium.

In the 'down' isomer the polar carbonyl group stands a good distance from the surrounding non-polar alkyl framework, which helps to avoid Van-der-Waals repulsion. The Cyclohexyl moeity is also in an ideal chair form, and is in free space away from possible steric clashes. The molecule has a large number of positive Van-der-Waals interactions. For the 'Up' isomer the carbonyl oxygen sits close to a methyl group which likely increases the steric energy, and the cyclohexyl moeity is twisted particularly at the carbons that join it to the main ring, where torsion (the displacement of the dihedral angle from ideal) is in excess of 18o. Because the downward facing carbonyl interacts repulsively with the groups on the underside of the main ring it is twisted outwards, leading to bond angles far from their ideal value, particularly in the cyclopentyl group where most of the bond angles are 10o smaller than their ideal values. This makes the 'down' isomer the thermodynamically more stable isomer, so on standing under equilibrating conditions the down isomer is formed.

B. Hyperstability

The Alkene in the precursor is said to react very slowly under reduction conditions. Clearly, access to the 'out' face of the alkene is good, so the reaction would be expected to proceed with good regioselectivity under cis alkylation conditions such as Pd/C or with a reduction such as dissolving metal. The Geometry of the Alkene is very flat, and one side is held in a five membered ring. the bond angles for the alkene are 114o and 117o, which are not far from the ideal 120o. After the face selective hydrogenation however the alkane formed must now be contorted into an awkward shape because instead of having a convenient flat profile the alkane is forced by the cyclopentyl ring to point into the inside of the molecule, creating steric clashes.

Hydrogenated taxol intermediate

This increase in bond torsion and strain increases the relative energy of the reduced product significantly. hydrogenation typically proceeds readily for most alkenes, with negative enthalpy change. however because the hydrogenation product has high energy the enthalpy of hydrogenation is small, or even positive. The reaction therefore proceeds very slowly and requires extreme conditions to force the reaction because the gibbs energy change is small

References

3. Regioselective addition of dichlorocarbene

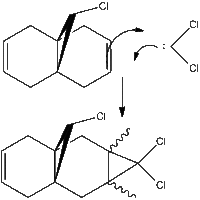
In the reaction of the bicyclic diene [12] with dichlorocarbene there are nucleophillic sites for dichlorocarbene to attack, leading to a dichlorocyclopropane. An analysis of the diene[12] is undertaken to establish which double bond is most electrophillic and therefore which product will be major. the reaction with dichlorocarbene is kinetic as carbenes are not long lived species. the stereochemistry of the product is not analysed in detail; for the mechanism shown the dichlorocarbene will likely react with the open face of the diene away from the chlorine, as the lone pairs on the dichlorocarbene will likely experience repulsion from the lone pairs on the chlorine. If the other double bond is attacked then this will not be the case.

A. Molecular Orbital Calculations

The Structure was optimised, then the MOs were calculated using the MOPAC/PM6 method. The HOMO was of particular interest as this indicates the possible relative reactivity of the two double bonds. the molecule was designated Cs symmetry, which was used by the calculation to stop the structure from breaking symmetry.

The Key MOs

MO	image	Analysis
HOMO-1		this is a pi bonding orbital on the alkene exo to Cl
HOMO		this is a pi bonding orbital on the alkene nearest to Cl
LUMO		a pi* orbital, antibonding on the double bond exo to Cl
LUMO+1		the C-Cl sigma* orbital
LUMO+2		The pi* orbital for the alkene nearest to Cl

The Chemistry of the molecule can be elucidated from the Frontier molecular orbitals. If Electrophillic dichlorocarbene were to attack the molecule the most likely site of attack is at the most electron rich site. The HOMO is the highest energy occupied orbital, and in this case is the pi bonding orbital nearest to Cl. This site is where there will be the greatest lowering of energy from reactants to products. the lone pair on dichlorocarbene must also attack a vacant orbital in order to complete the reaction. the LUMO+2 is the pi* orbital for that double bond, which is close in energy to the HOMO, so as the HOMO interacts with the vacant orbital on the carbene the carbene lone pair is interacting with the pi* LUMO+2 breaking the bond.

B. Vibration frequency Prediction

Predicted IR stretching frequencies for molecule 12

Assignment	Diene (12)	Hydrogenated product (12a)
C-Cl	770.95	775.06
C=C (endo)	1757.37	1758.07
C=C (exo)	1737.12	N/A
spectrum

Comparing the Alkene stretching frequencies for the diene (12) there is a difference of 20cm-1 between the two double bonds. The double bond endo (nearest the chlorine) has the higher stretching frequency, indicating that there is more electron density making the bond stiffer. This suggests that the site would be more readily attacked by electrophiles. The stretching frequency of the C-Cl bond increases slightly on hydrogenation of the exo double bond.

for the non Hydrogenated molecule the HOMO-1 orbital is a pi bond on the exo double bond, but also has some antibonding character on the C-Cl bond. Furthermore, this orbital can donate electron density to the LUMO+1, the C-Cl antibonding orbital, further weakening it and shifting its stretching frequency lower.

With that double bond hydrogenated there is now no donation from the pi orbital into the C-Cl antibonding orbital. converting from cm-1 to kjmol-1 the interaction was worth 0.049kjmol-1. Furthermore the double bond nearest the chlorine has almost exactly the same stretching frequency as the diene, indicating that there was no correlation between the two double bonds, either directly or via another orbital such as the C-Cl antibonding orbital.

References

4. Monosaccharide Chemistry; Glycosidation

Introduction

File:Alpha-D-glucopyranose-2D-skeletal.png

In the synthesis of functionalised monosaccharides and oligosaccharides the most important stereogenic center is the anomeric center. this is the 1 position of the saccharide ring. the anomeric effect is the tendency for the hydroxyl to prefer the conformation shown because the ether oxygen lone pair can donate into the C1-OH sigma* orbital, lowering the energy by 3-5 kcal/mol. when synthesising oligosaccharides control of the anomeric position's stereochemistry is a must. in order to do so the more reactive anomeric oxygen on C1 is methylated using the Fisher methylation process, then the other hydroxyls are acetylated under orthogonal conditions. the anomeric methoxy is later converted to the bromide which is removed with silver triflate to form the acylium cation, namely structures A and B. the control of stereochemistry is achieved by the acetyl group attacking the anomeric position forming the fused bicyclic intermediates C and D, which are then attacked enantioselectively by nucleophiles to give the correct stereochemistry glycosides in good enantiomeric excess.

To Model the Monosaccharides methyl groups were used as the 'R' groups as they remove any hydrogen bonding interactions, have reasonable size and only add 8 electrons per group to the computation (compared to hyroxyl). Using an Acetyl group would add 19 electrons relative to a hydroxyl, which is not ideal if the computation time increases with the square of the number of electrons.

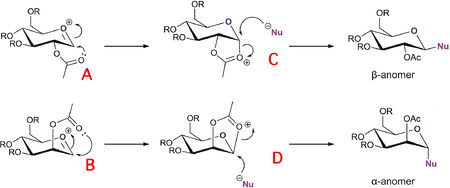
The MM2 method is not very useful in determining the relative energies between the pairs of isomers / conformers because the two structures are intermediates and their conformation depends critically on the interaction between the acetyl group and the acylium cation. The MM2 method is not very successful at accommodation electronic effects such as these because its modelling systems don't include concepts such as conjugated bonds, rather it simply attempts to configure the atoms such that bond angles, dihedral angles and bond lengths are as close as possible to 'ideal' values which the program has stored for a range of atom types. The MOPAC/PM6 method takes more account of electronics, by using a semi-empirical approximation of the orbitals that are constructed by the program for each atom from the program's datasets. Because it uses orbitals tt is able to find the conformation that chemical intuition suggests where conjugation and lone pairs are important.In the sugar molecules this translates to the acetyl group forming a 5 membered open ring with the acylium cation.

Structures A&B

MM2 and PM6 optimisations for each sugar conformer

glycoside label	chemdraw structure	MM2 data	MM2 JMOL	PM6 data	PM6 JMOL
A		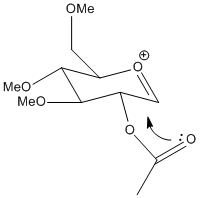Stretch: 2.5469 Bend: 12.0007 Stretch-Bend: 0.9972 Torsion: 3.0135 Non-1,4 VDW: 1.5286 1,4 VDW: 19.3534 Charge/Dipole: -33.2431 Dipole/Dipole: 8.0025 Total Energy: 14.1995 kcal/mol	JMOL	-88.82	JMOL
A'	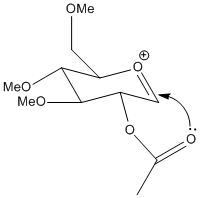cell	Stretch: 2.4483 Bend: 12.0800 Stretch-Bend: 0.9882 Torsion: 1.5941 Non-1,4 VDW: -1.8096 1,4 VDW: 17.9515 Charge/Dipole: 0.2081 Dipole/Dipole: 5.5712 Total Energy: 39.0317 kcal/mol	JMOL	-85.82	JMOL
B	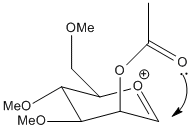cell	Stretch: 2.5488 Bend: 11.9969 Stretch-Bend: 0.9974 Torsion: 3.0088 Non-1,4 VDW: 1.5223 1,4 VDW: 19.3504 Charge/Dipole: -33.2265 Dipole/Dipole: 8.0018 Total Energy: 14.1999 kcal/mol	JMOL	-90.51	JMOL
B'	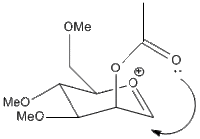cell	Stretch: 2.4383 Bend: 11.6410 Stretch-Bend: 0.9597 Torsion: 2.1287 Non-1,4 VDW: -1.4231 1,4 VDW: 18.6847 Charge/Dipole: -8.7498 Dipole/Dipole: 6.0522 Total Energy: 31.7317 kcal/mol	JMOL	-74.82	JMOL

A' is a very shallow local minimum, and the PM6 calculation was able almost all the time to collapse back to the ideal A form. However, in the calculation presented the energy is given as almost identical to the untwisted version. this is because the ether oxygen is coordinating to the acylium cation, not the acetyl. this alternate coordination blocks access to that side of the cation the same way the acetyl would, slightly reducing selectivity.

The relative energies were then used to calculate the populations according to the boltzmann distribution. Given the large energy difference between A and A', and between B and B', the populations of A' and B' were less than 1_x10^-4%

Ring intermediates C&D

Energies and structures for intermediates C&D, C' & D'

label	Structure	MM2 data	MM2 JMOL	PM6 data	PM6 JMOL
C		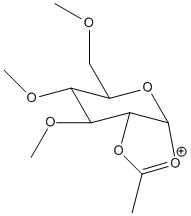Stretch: 1.9605 Bend: 12.4799 Stretch-Bend: 0.6625 Torsion: 9.2194 Non-1,4 VDW: -3.9886 1,4 VDW: 18.3558 Charge/Dipole: -5.7669 Dipole/Dipole: -1.3317 Total Energy: 31.5909 kcal/mol	JMOL	-88.58235	JMOL
C'		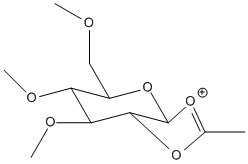Stretch: 2.6297 Bend: 19.9188 Stretch-Bend: 0.7873 Torsion: 6.5851 Non-1,4 VDW: -2.9999 1,4 VDW: 18.5365 Charge/Dipole: -1.1216 Dipole/Dipole: -1.2679 Total Energy: 43.0678 kcal/mol	JMOL	-66.0294	JMOL
D		Stretch: 1.9356 Bend: 13.1144 Stretch-Bend: 0.6587 Torsion: 8.4647 Non-1,4 VDW: -2.6658 1,4 VDW: 17.9641 Charge/Dipole: -9.9415 Dipole/Dipole: -2.6948 Total Energy: 26.8354 kcal/mol	JMOL	-91.49840	JMOL
D'		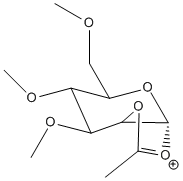Stretch: 2.7294 Bend: 18.0344 Stretch-Bend: 0.8456 Torsion: 7.8591 Non-1,4 VDW: -2.1942 1,4 VDW: 19.1295 Charge/Dipole: -3.1645 Dipole/Dipole: -0.0247 Total Energy: 43.2146 kcal/mol	JMOL	-67.64187	JMOL

The relative energies were then used to calculate the populations according to the boltzmann distribution. Given the large energy difference between C and C', and between D and D', the populations of C' and D' were less than 1_x10^-11%

Whilst the energies of the pre-transition state structures A, A', B and B' demonstrated that forming twisted structures was energetically unfavourable, with energy differences greater than 10kcal/mol (Far greater than that accessible through thermal excitation), the intermediates C,C', D and D' demonstrate that the formation of trans lactones is also very unfavourable, with a difference in energy of 10kcal/mol. In the reaction to form the intermediate there is solvent interaction, so the acetyl group is in competition with solvent to attack the acylium cation. if the solvent is nucleophillic like methanol or water then the reaction is under thermodynamic control, and the trans isomers will be hugely disfavoured in the equilibrium.

C. Stereoselectivity

In all cases the 'twisted' trans transition state ring is significantly higher in energy than the 'cis' ring transition state for structures C and D, and the same is true for the Pre-transition state structures A and B, where A' and B' have higher steric energies than their untwisted counterparts A and B. there are several reasons why observed stereoselectivity is so high which can be inferred from the calculation results. in the pre-transition-state species A and B, there is a barrier to rotation for the acetyl group for both species, as they must twist past the neighbouring C-H bond. In order for the acetyl lone pair to react successfully it must reach the critical angle of 107o relative to the acylium cation (in order to react with the pi* orbital), which involves considerable stretching and bond angle contortion. in order to reach that far onto the other side of the pyranose ring the ring itself must change from a favourable half chair into something more akin to a half-boat structure, which creates steric clashes for the OMe groups on the ring. Even if the Acetyl group crosses all these barriers to reaction, the transition state ring it forms is still thermodynamically higher in energy as C' and D' than for C and D. In short, the reaction is kinetically and thermodynamically forbidden!

References

DFT based mini project

Please click through!