Rep:Mod:tf910
Module 3
Introduction
This project involved the analysis and characterisation of the transition states on a Potential Energy Surface for the Cope rearrangement and a Diels-Alder Cycloaddition reaction. This will be done using computational chemistry to examine energy minima of transition states as well as reactants and products and also the effect of orbital interactions on transition state enrgies will be looked at. The real aim is to use these calculations to get a better understanding of these reaction mechanisms and to try to identify why certain transition state structures or reaction products may be favoured over one another.
The program used to carry out these calculations is GaussView 5.0 which enable the modelling of the PES by calculating total energies of the system. GaussView is used to determine the optimal structure of the molecules which participate in reactions.
This project looks at the following two reactions: (i) Cope Rearrangement (ii) Diels-Alder Reaction
The Cope Rearrangement
The Cope rearrangement reaction was named after Arthur Cope who in 1940 discovered that when a 1,5-diene is heated it undergoes a 3,3-sigmatropic rearrangment into an equivalent and more energetically stable regioisomer. The mechanism is an example of a concerted pericyclic reaction. The transition state structures can be either a chair or a boat as seen below:
Optimisation and Analysis of 1,5-hexadiene
Anti conformation
The anti conformer of 1,5-hexadiene was drawn using Gaussview and consequently it was optimised using the Hartree-Fock method with a 3-21G basis set. The calculation was run on the HPC server.
D-Space - http://hdl.handle.net/10042/24057
Optimised anti 1,5-hexadiene
A summary of the data from the optimisation can be seen below:
After symmetrizing, the point group was found to be C2
Energy: -231.69260235 a.u.
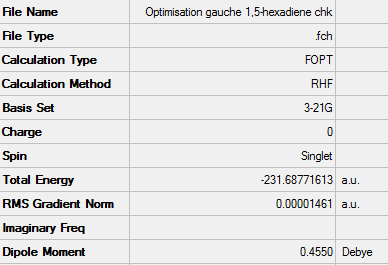
Gauche conformation
As for the anti conformer, the gauche conformer was also drawn using Gaussview and it was optimised using the Hartree-Fock method with a 3-21G basis set. The calculation again was run on the HPC server.
D-Space - http://hdl.handle.net/10042/24061
Optimised gauche 1,5-hexadiene
A summary of the data from the optimisation can be seen below:
After symmetrizing, the point group was found to be C2
Energy: -231.68771613 a.u.
The Gauche conformer was found to have a higher total energy compared to the anti conformer. The main reason for this is the steric repulsion of the terminal alkene groups which are nearer to each other in the Gauche conformation and so experience greater steric clashing.
Lowest Energy Conformation
Table from Appendix 1:[1]
| Conformer | Structure | Point Group | Energy (a.u.) |
|---|---|---|---|
| Gauche 1 |  |
C2 | -231.68772 |
| Gauche 2 |  |
C2 | -231.69167 |
| Gauche 3 |  |
C1 | -231.69266 |
| Gauche 4 |  |
C2 | -231.69153 |
| Gauche 5 |  |
C1 | -231.68962 |
| Gauche 6 |  |
C1 | -231.68916 |
| Anti 1 |  |
C2 | -231.69260 |
| Anti 2 |  |
Ci | -231.69254 |
| Anti 3 |  |
C2h | -231.68907 |
| Anti 4 |  |
C1 | -231.69097 |
Ci Anti Conformer
DFT 3-21G Basis Set
The Ci Anti Conformer was optimised using a Hartree Fock method with a 3-21G basis set. The calculation was run on the HPC server.
D-Space - http://hdl.handle.net/10042/24066
3-21G Optimised anti 1,5 hexadiene (Ci symmetry)
A summary of the 3-21G DFT optimisation can be seen below:
DFT 6-31G(d) Basis Set
The Ci Anti Conformer was further optimised using a DFT method with a 6-31G(d) basis set. The calculation was again run on the HPC server.
D-Space - http://hdl.handle.net/10042/24078
6-31G(d) Optimised anti 1,5 hexadiene (Ci symmetry)
A summary of the 6-31G(d) DFT optimisation can be seen below:
This is indicative that when using the higher level basis set, the energy of the molecule is decreased leading to a more stable molecule. The 6-31G(d) basis set also gives an energy value which is closer to the literature value.The results indicate that when using the higher level basis set, it decreases the energy of the molecule which corresponds to a more stable molecule. Using the 6-31G basis set also gives a value of the energy which is closer to the literature value.[2] The values of the bond lengths for C-H and C-C also differ slightly.
Frequency Analysis
Frequency analysis is vital in computational chemistry as it can be used to calculate the minimum structure on the potential energy surface. When the frequencies are positive, it corresponds to the minimum but if one or more of the values are negative it corresponds to the transition state.
The optimized Ci was consequently used for frequency analysis. The aim of this was to present the minimum critical point on the potential energy surface producing positive real values for the vibrational frequencies. The calculation was run on a HPC server.
D-Space - http://hdl.handle.net/10042/24089
Low frequencies --- -18.8144 -11.7180 -0.0009 -0.0005 -0.0001 1.7514 Low frequencies --- 72.7146 80.1401 120.0114
Zero-point correction= 0.142491 (Hartree/Particle) Thermal correction to Energy= 0.149847 Thermal correction to Enthalpy= 0.150791 Thermal correction to Gibbs Free Energy= 0.110881 Sum of electronic and zero-point Energies= -234.469212 Sum of electronic and thermal Energies= -234.461856 Sum of electronic and thermal Enthalpies= -234.460912 Sum of electronic and thermal Free Energies= -234.500822
IR Spectrum of anti 1,5 hexadiene (Ci symmetry):
The IR spectrum shows that there are 21 visible peaks. From the output file there are in reality 41 vibrations. However for an IR peak to be visible, the vibration must lead to a change in dipole moment.
| Equation and Values | ||||
| Property | Equation | Value | ||
| Sum of electronic and zero-point Energies | E(0 K) = Eelec + ZPE | -234.469202 | ||
| Sum of electronic and thermal Energies | E(298.15 K) = E(0 K) + Evib + Erot + Etrans | -234.461855 | ||
| Sum of electronic and thermal Enthalpies | H = E (298.15K) + RT | -234.460911 | ||
| Sum of electronic and thermal Free Energies | G = H - TS | -234.500777 | ||
Optimizing the "Chair" and "Boat" Transition Structures
Hessian Method
The guess transition state structure for the chair transition state was created, two allyl fragments were created and positioned in a chair transition state like structure at a distance of 2.20Å between the terminal carbons.
D-Space - http://hdl.handle.net/10042/24127
Structure of optimised chair conformation using Hartree Fock and the default basis set 3-21G
A summary of the results from the optimisation can be seen below:
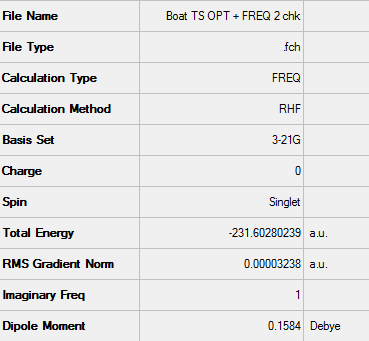
Low frequencies --- -817.9780 -3.5381 -1.0454 -0.0003 0.0001 0.0006 Low frequencies --- 1.1742 209.4810 395.9153 ****** 1 imaginary frequencies (negative Signs) ******
Sum of electronic and zero-point Energies= -231.466700 Sum of electronic and thermal Energies= -231.461340 Sum of electronic and thermal Enthalpies= -231.460396 Sum of electronic and thermal Free Energies= -231.495206
The imaginary frequency which is caused by the vibration at -817.98 cm-1 corresponds to what would be expected in the Cope rearrangement.
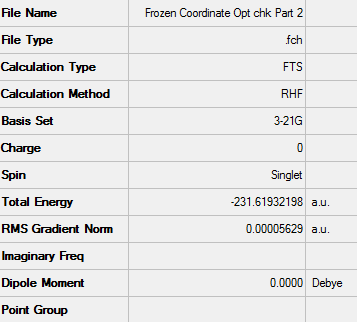
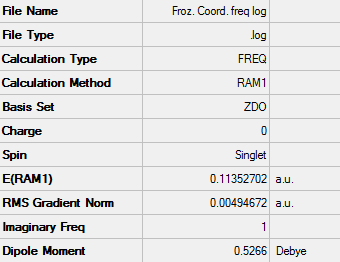
Frozen Coordinate Method
A chair transition state structure (using the optimised allyl fragment) was drawn. This method involved the fixing of the coordinates between the two terminal atom pairs of the allyl fragment which form the TS. They were fixed to approximately 2.20 Å. To do this the redundant coordinates were set to Bond and Freeze Coordinates. Using a Hartree Fock method with a 3-21G basis set the structure was optimised on the HPC server.
D-Space - http://hdl.handle.net/10042/24132
Structure of proposed chair TS optimised by frozen coordinate method
The summary of the calculation can be seen below:
Having carried out the first optimisation, the coordinates were unfrozen and the set to Bond and Derivatives. By doing this the bonds which were previously frozen were optimised by finding the derivative along the PES.
D-Space - http://hdl.handle.net/10042/24138
Structure of the fully optimised chair TS by frozen coordinate method
The summary of the optimisation can be seen below:
Optimisation and Frequency Analysis of Boat
QST2 Method
In order to optimise the boat structure an alternative method was used. Two molecules of the previously optimised Ci anti conformer of 1,5-hexadiene were numbered so as one resembled a product and the other a reactant. The calculation was run as a QST2 TS optimisation using a Hartree Fock method and a 3-21G basis set. The optimisation was unsuccessful due to the fact that the GaussView software is unable to consider the possibility of rotation around the central bonds but only translated the top allyl fragment.
D-Space - http://hdl.handle.net/10042/24138
Structure of the unsuccessfully optimised boat
The summary of the optimisation can be seen below:
To correct this previous error, the reactant and product geometries were modified so that they all resembled the boat transition structure more closely. The central C-C-C-C dihedral angle was changed to 0°. Then the inside C-C-C angles were reduced to 100°. The calculation was again run as a QST2 TS optimisation using a Hartree Fock method and a 3-21G basis set.
D-Space - http://hdl.handle.net/10042/24158
Structure of the optimised boat conformation
The summary of the optimisation can be seen below:
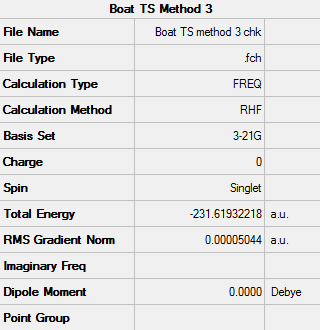
Low frequencies --- -839.9283 -8.0754 -6.3113 -4.0796 0.0003 0.0003 Low frequencies --- 0.0006 155.0909 382.2138 ****** 1 imaginary frequencies (negative Signs) ******
Imaginary vibration at -839.93 cm-1
This method was successful to fully optimise the boat TS but as indicated from the first optimisation, there are issues which need to be addressed in order to achieve a successful optimisation. The product and reactant input need to closely resemble the boat TS structure.
Intrinsic Reaction Coordinate and Analysis of the Chair TS
When looking at the optimised reactant and product structures as well as the Transition state structures it is not possible to determine whether they connect to form gauche or anti structures of 1,5-hexadiene.
The use of an IRC analysis is to determine the local minimum point to the saddle transition state. In order to achieve this the minimum energy pathway from the transition state to the aforementioned local minimum point is monitored.
During the calculation the molecule's geometry is changed following the steepest section of the reaction energy surface. An IRC was run on the previously optimised chair structure of 1,5-hexadiene to determine the conformation of the structure it forms.
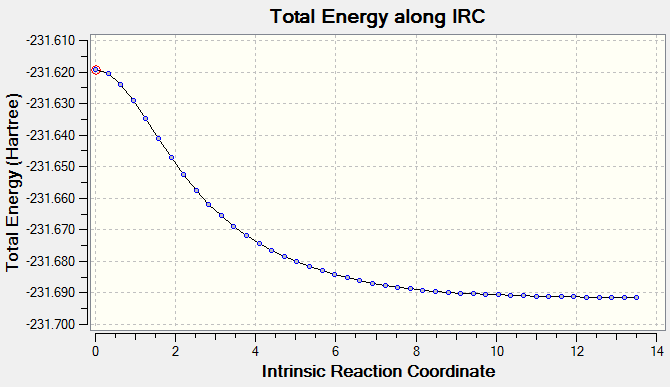
Initially in the IRC, 50 steps were carried out in the forward direction.
D-Space - http://hdl.handle.net/10042/24234
50 Step Chair Transition State Iteration Sequence
The lowest total Energy = -231.69157873 a.u.
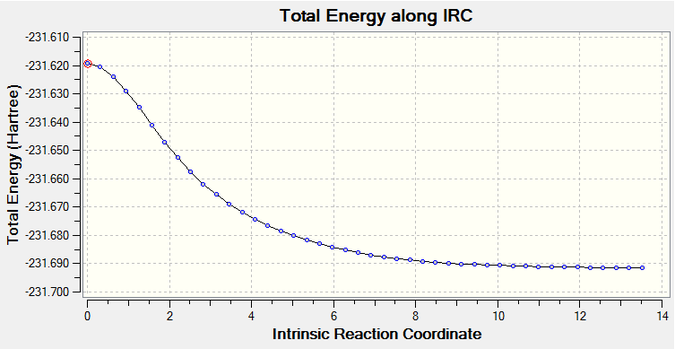
The IRC using 50 steps did not reach a minimum after the calculation and so it was run again using 100 steps along the reaction coordinate. The resultant structure of lowest energy was hence optimised and then compared to the conformers. It resembled the second gauche conformer (see table above).
D-Space - http://hdl.handle.net/10042/24231
100 Step Chair Transition State Iteration Sequence
The lowest total Energy = -231.69156538 a.u.
Activation Energy
Chair Optimisation
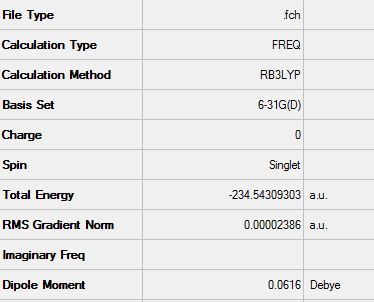
The chair was optimised using the higher 6-31G basis set with a DFT method (B3LYP). The optimisation was run on HPC.
D-Space - http://hdl.handle.net/10042/24175
Optimised structure of chair conformer using 6-31G basis set
The summary of the optimisation can be seen below:
Chair Frequency Analysis
The frequency analysis of this chair conformation was done using the previously optimised chair orientation transition state using DFT method with a 6-31G(d) basis set.
D Space - http://hdl.handle.net/10042/24208
The low frequency values have copied from the output file and show that the frequency calculation is finished with one imaginary frequency.
Low frequencies --- -564.9382 -0.0007 0.0006 0.0006 21.3168 26.5951 Low frequencies --- 39.4745 194.3347 268.6930 ****** 1 imaginary frequencies (negative Signs) ******
Zero-point correction= 0.142061 (Hartree/Particle) Thermal correction to Energy= 0.147980 Thermal correction to Enthalpy= 0.148924 Thermal correction to Gibbs Free Energy= 0.113178 Sum of electronic and zero-point Energies= -234.414924 Sum of electronic and thermal Energies= -234.409005 Sum of electronic and thermal Enthalpies= -234.408061 Sum of electronic and thermal Free Energies= -234.443808
The Imaginary Frequency vibration at -564.9382 cm-1
Boat Optimisation
The boat conformation was also optimised using the higher 6-31G basis set with a DFT method (B3LYP). The optimisation was run on HPC.
D-Space - http://hdl.handle.net/10042/24179
Optimised structure of boat conformer using 6-31G basis set
A summary of the optimisation can be seen below:
Boat Frequency Analysis
The frequency analysis of this boat conformation was carried out using the previously optimised chair orientation transition state using DFT method with a 6-31G(d) basis set.
D-Space - http://hdl.handle.net/10042/24214
Low frequencies --- -530.3618 -8.3908 0.0006 0.0008 0.0010 15.4632 Low frequencies --- 17.6137 135.6121 261.7006 ****** 1 imaginary frequencies (negative Signs) ******
Zero-point correction= 0.140751 (Hartree/Particle) Thermal correction to Energy= 0.147086 Thermal correction to Enthalpy= 0.148030 Thermal correction to Gibbs Free Energy= 0.111341 Sum of electronic and zero-point Energies= -234.402342 Sum of electronic and thermal Energies= -234.396008 Sum of electronic and thermal Enthalpies= -234.395063 Sum of electronic and thermal Free Energies= -234.431752
The Imaginary Frequency vibration at -530.3618 cm-1
Chair and Boat Comparison
Energy Summary
A summary of the total energies in each system after each optimization at a given temperature (Hartrees)
| HF/3-21G | B3LYP/6-31G* | |||||
|---|---|---|---|---|---|---|
| Electronic energy | Sum of electronic and zero-point energies at 0 K | Sum of electronic and thermal energies at 298.15 K | Electronic energy | Sum of electronic and zero-point energies at 0 K | Sum of electronic and thermal energies at 298.15 K | |
| Chair TS | -231.619322 | -231.466705 | -231.461346 | -234.556983 | -234.414919 | -234.408998 |
| Boat TS | -231.602802 | -231.450929 | -231.445300 | -234.543093 | -234.402340 | -234.396006 |
| Reactant (anti2/Ci) | -231.692535 | -231.539539 | -231.5322566 | -234.611710 | -234.469203 | -234.461856 |
A summary of the activation energies after each optimisation at given temperatures (in kcal/mol)
| HF/3-21G at 0 K (ΔE (kcal/mol)-1) | HF/3-21G at 298.15 K (ΔE (kcal/mol)-1) | B3LYP/6-31G* at 0 K (ΔE (kcal/mol)-1) | B3LYP/6-31G* at 298.15 K (ΔE (kcal/mol)-1) | Experimental Values [4](ΔE(kcal/mol)-1) | |
| ΔE (Chair) | 45.7 | 45.3 | 34.1 | 33.7 | 33.5 ± 0.5 |
| ΔE (Boat) | 55.6 | 50.3 | 42.0 | 37.6 | 44.7 ± 2.0 |
By using a higher level basis set, it is possible to get a better picture of the system and its energy. From the results it may be suggested that the favoured reaction pathway is one with a chair transition state structure because it has a lower activation energy. The reaction can possibly go via a boat transition state under thermodynamic conditions becasue more thermal energy is required to get over the energy barrier. Using this argument, kinetically the chair transition state structure is preferred as less thermal energy is required.[3] The sum of the electronic and zero-point energies of the molecules are lower than the sum of the electronic and thermal energies due to the fact that at 0 K there aren't thermal vibrations.
The Diels-Alder Cycloaddition
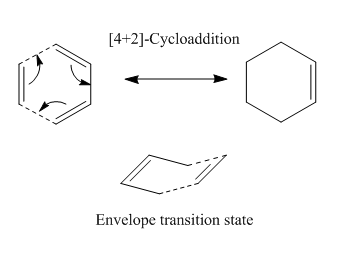
An example of the simplest Diels-Alder cycloaddition can be seen below with a concerted pericyclic mechanism to form the product via a envelope-like transition state.
In organic chemistry, the Diels-Alder reaction is a famous example of a cycloaddition reaction. It involves the concerted [4+2] addition of a conjugated diene and an alkene dienophile to form two new carbon-carbon bonds. This reaction is often strategically used in synthesis because of the fact that it is regio- and stereo-selective. The reaction occurs via a 6-membered transition state which has two possible conformers - exo and endo. In order to allow favourable orbital overlap between the reactants the diene has to be in the cis conformation - this is to maximise the HOMO/LUMO interaction to form two new σ bonds and a π bond. The rate and other characteristics of the reaction can be governed by the use of appropriate electron donating/withdrawing groups.
GaussView will be used to study two Diels-Alder reactions and to characterise the TS and visualise the HOMO and LUMO orbitals.
The Addition of Ethylene to Cis-butadiene
Optimisation of Cis-butadiene
Cis-Butadiene was drawn in GaussView and then optimised using the AM1 semi-empirical molecular orbital method. The calculation was run on the HPC server.
D-Space - http://hdl.handle.net/10042/24241
A summary of the optimisation can be seen below:
Energy (RAM1) = 0.04879719
Point Group - C2v
Optimisation of ethene
Ethene was then drawn in GaussView and also optimised using the AM1 semi-empirical molecular orbital method. The calculation was run on the HPC server.
D-Space - http://hdl.handle.net/10042/24242
A summary of the optimisation can be seen below:
In the case of both of the reactants their optimisations both show an RMS gradient of approximately 0.00001 which is indicative that the optimisations have gone to completion.
Energy (RAM1) = 0.02619024
Point Group -' D2h
The MOs for the HOMO and LUMO of ethene and cis-butadiene can be seen in the table below:
| Type of MO | Visualised MO | Symmetry of MO | Energy (au) |
|---|---|---|---|
| cis-Butadiene HOMO |  |
Anti-symmetric | -0.34381 |
| cis-Butadiene LUMO |  |
Symmetric | 0.01707 |
| Ethene HOMO |  |
Symmetric | -0.38777 |
| Ethene LUMO |  |
Anti-symmetric | 0.05284 |
The below diagram shows the frontier orbitals of cis-butadiene and the MO diagram for ethene:
Optimal Transition State Structures using a Frozen Coordinate Method
The transition state structure for this Diels-Alder cycloaddition reaction is meant to be envelope-like. The structure was optimised using the semi empirical AM1 system using the frozen coordinate method which was used previously with the terminal carbons set at a distance of 2.20 Å from each other.
D-Space - http://hdl.handle.net/10042/24256
Frequency Analysis
Frequency analysis was also conducted using the same method and basis set.
D-Space - http://hdl.handle.net/10042/24258
A summary of the frequency analysis can be seen below:
As can be seen from the table above there is an imaginary frequency present at -977.89 cm-1. This indicates the presence of a transition state.
Vibration corresponding to -977.89 cm-1 which indicates the transition state structure
The low frequency values have been presented from the output log file and show that the frequency calculation is complete:
Low frequencies --- -977.8947 -79.0965 -60.7487 -0.0418 -0.0022 0.0091 Low frequencies --- 9.0873 140.4152 237.8229 ****** 1 imaginary frequencies (negative Signs) ******
Zero-point correction= 0.141403 (Hartree/Particle) Thermal correction to Energy= 0.147729 Thermal correction to Enthalpy= 0.148674 Thermal correction to Gibbs Free Energy= 0.111992 Sum of electronic and zero-point Energies= 0.254930 Sum of electronic and thermal Energies= 0.261257 Sum of electronic and thermal Enthalpies= 0.262201 Sum of electronic and thermal Free Energies= 0.225519
The vibration seen above corresponds to the formation of the new sigma bond and the loss of a pi bond. The ethene molecule in the reaction changes hybridisation from sp2 to sp3. This vibration highlights how the ethene interacts with the butadiene and provides insight into how the HOMO and the LUMO orbitals are alligned when they interact to form the bonds. The terminal bond length is greater than is recorded in literature which suggests the C-C bond has not formed - however it is small enough in length to suggest that an orbital interaction is taking place.
Comparison of Transition State Structures
When the bond lengths are compared with the respective calculation methods and the literature values of actual bond lengths it gives an indication on the nature of the transition state. [4]
Looking at the methods used the DFT (6-31G(d)) basis set gave a much higher value for the terminal C-C bonds which is closer to the literature value than the Semi-Empirical (AM1) method.
Because of the fact that the DFT terminal bond length is longer it is suggestive that the transition state is earlier with respect to the semi-empirical structure.
In the transition state the double bonds of the ethene and the cis-butadiene fragments have longer bond lengths than the would be typically expected for C=C though it is not as long as the C-C single bonds as is predicted.
MO Analysis of Envelope Transition State
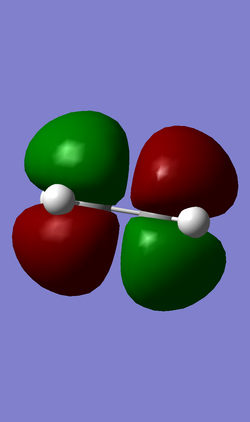
The HOMO Molecular Orbital (Energy = -0.32394 a.u.)
The LUMO Molecular Orbital (Energy = -0.02316 a.u.)
The HOMO molecular orbital is symmetrical and weakly bonding and this can be justified from the number of nodes present. From this we know that the fragment orbitals which overlap are both antisymmetric .
The LUMO molecular orbital is antisymmetric with respect to the symmetry plane and has a higher number of nodes - for this reason it can be seen to be antibonding.
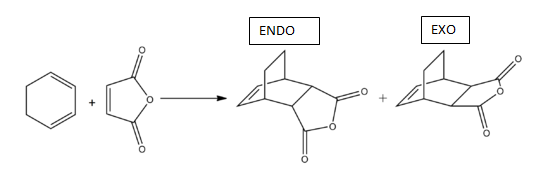
Reaction of Cyclohexadiene with Maleic Anhydride
The scheme for the reaction of cyclohexadiene and maleic anhydride can be seen below showing the two possible products:
When looking at the reaction between cyclohexadiene and maleic anhydride, mechanisms can be feasibly drawn to show the formation of the endo or exo product. When performed in the lab the endo product is found to be the kinetically favoured product whereas the exo product is thermodynamically favoured.[5] The kinetic preference to the endo product can be explained by orbital interactions in the transition state which can be examined using computational calculations done on GaussView.
Optimising Maleic Anhydride and Cyclohexadiene Fragments
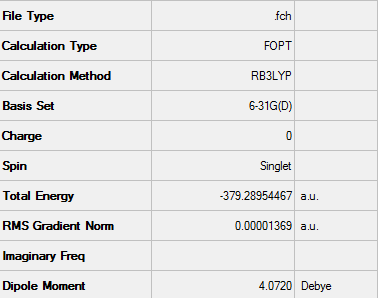
Prior to the construction of the guess endo and exo transition states, both of the reactant fragments were optimised using the DFT method with a 6-31G(d) basis set. The calculation was run on the HPC server.
D-Space - http://hdl.handle.net/10042/24315
Structure of optimised maleic anhydride using 6-31G(d) basis set
A summary of the optimisation data can be seen below:
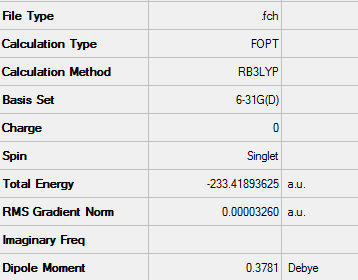
The cyclohexadiene was optimised in the same way as the maleic anhydride fragment, that is to say using the DFT method with a 6-31G(d) basis set. Again the calculation was run on the HPC server.
D-Space - http://hdl.handle.net/10042/24316
Structure of optimised cyclohexadiene using 6-31G(d) basis set
A summary of the optimisation data can be seen below:
The HOMOs and LUMOs for both fragments have been visualised in GaussView and are presented in the table below:
| Type of MO | Visualised MO | Symmetry | Energy (a.u.) |
|---|---|---|---|
| Maleic Anhydride HOMO |  |
Symmetric | -0.29928 |
| Maleic Anhydride LUMO |  |
Anti-symmetric | -0.11712 |
| Cyclohexadiene HOMO |  |
Anti-symmetric | -0.20551 |
| Cyclohexadiene LUMO |  |
Symmetric | -0.01710 |
If you analyse the molecular orbitals of both fragements you can see that the HOMO of maleic anhydride is strongly bond - largely due to the favourable bonding interactions which are seen on the ring and the oxygens. On the other hand the LUMO consists mainly of antibonding interactions and this is highlighted by the number of nodes which are present on the alkene and carbonyl bonds.
Looking at the cyclohexadiene fragment, the HOMO is symmetrical and has a node in the centre. Antibonding interactions are evident although there are also some bonding interactions which would imply that the MO is weakly bonding. Looking at the LUMO it is clearly symmetrical and antibonding interactions dominate highlighted by the number of nodes.
Comparison of the energies of the respective HOMO and LUMO of maleic anhydride show there to be a large gap in energy compared to cyclohexadiene. Therefore maleic anhydride is able to accept electron density from the HOMO of cyclohexadiene. Since both orbitals are antisymmetric the interaction is allowed and favourable.
Analysis of Endo and Exo Transition States
EXO
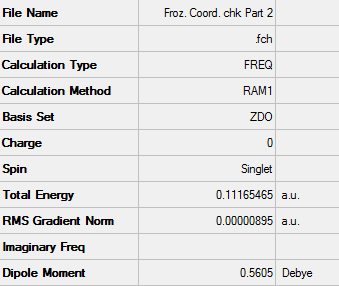
Taking the optimised fragments of maleic anhydride and cyclohexadiene, an exo transition state was drawn on GaussView. The terminal carbon atoms were frozen as done previously at 2.10 Å. The calculation was run on the HPC server.
D-Space - http://hdl.handle.net/10042/24323
A summary of the data from the calculation can be seen below:
Exo Frequency Analysis
D-Space - http://hdl.handle.net/10042/24321
Zero-point correction= 0.181203 (Hartree/Particle) Thermal correction to Energy= 0.191644 Thermal correction to Enthalpy= 0.192588 Thermal correction to Gibbs Free Energy= 0.144725 Sum of electronic and zero-point Energies= -612.495476 Sum of electronic and thermal Energies= -612.485035 Sum of electronic and thermal Enthalpies= -612.484091 Sum of electronic and thermal Free Energies= -612.531953
Low frequencies --- -466.4669 -31.5915 -24.1975 -0.0005 -0.0001 0.0005 Low frequencies --- 2.8268 46.8664 106.1689 ****** 1 imaginary frequencies (negative Signs) ******
Imaginary Frequency vibration at -466.47 cm-1
This vibration relates to the concerted formation of two sigma bonds
ENDO
The endo transition state was drawn on GaussView using the optimised fragments of maleic anhydride and cyclohexadiene. The same procedure was carried out as for the exo transition state.
D-Space - http://hdl.handle.net/10042/24325
A summary of the data from the calculation can be seen below:
Endo Frequency Analysis
D-Space - http://hdl.handle.net/10042/24327
Zero-point correction= 0.180921 (Hartree/Particle) Thermal correction to Energy= 0.190736 Thermal correction to Enthalpy= 0.191680 Thermal correction to Gibbs Free Energy= 0.145465 Sum of electronic and zero-point Energies= -612.487786 Sum of electronic and thermal Energies= -612.477970 Sum of electronic and thermal Enthalpies= -612.477026 Sum of electronic and thermal Free Energies= -612.523242
Low frequencies --- -480.7068 -52.3975 -41.9664 -30.8204 0.0007 0.0008 Low frequencies --- 0.0011 26.5110 78.9781 ****** 1 imaginary frequencies (negative Signs) ******
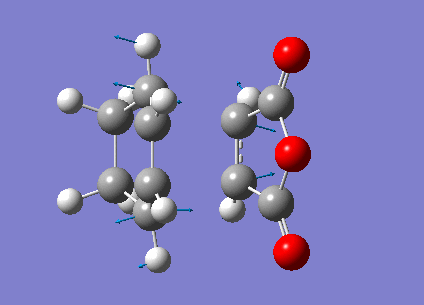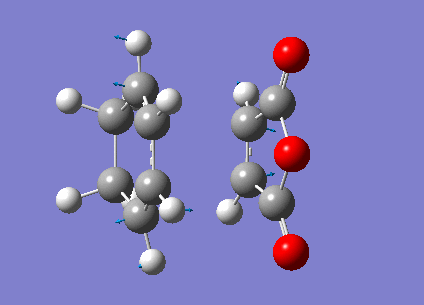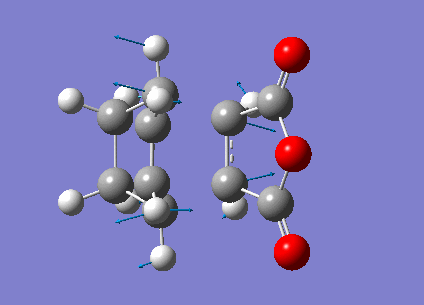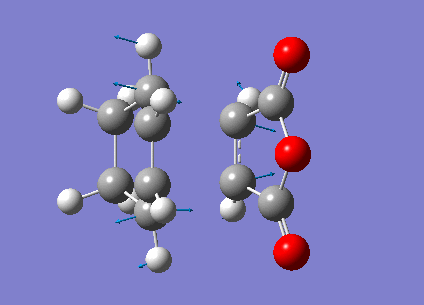Imaginary Frequency vibration at -480.71 cm-1
Discussion of Exo and Endo Transition State Structures
It has been generally mentioned that the endo product is kinetically favoured and the exo product is thermodynamically favoured and that it can be explained by the orbital interactions which produce a stabilising effect. From the calculations done on the optimised structures of the two products and the determination of the activation energies it is consequently possible to explain the characteristics in more detail.
| Parameter (Å) | Exo | Endo |
|---|---|---|
| C-C Inter-fragment Bond Length | 2.29 | 2.27 |
| Bond Length in Maleic Anhydride | 1.48 | 1.48 |
| Bond Length in cyclohexadiene | 1.53 | 1.54 |
| New C-C Bond Length | 1.40 | 1.39 |
| New C=C Bond Length | 1.40 | 1.40 |
| Through Space Distance | 2.96 | 2.87 |
The mechanism for the cycloaddition requires the movement of electrons which occupy π orbitals into σ orbitals while forming two new σ bonds and getting rid of two π bonds while a new π bond is also formed on the diene. The maleic anhydride alkene bond is also converted into a single C-C bond.
Bond Lengths
The double bond which is formed in the two structures both have the same length at 1.40 Å in the exo and endo transition state. The C=C bond which is converted into a single C-C bond also has length of 1.40 Å in both transition states. This is different from the literature values where a C=C bond is usually 1.34 Å and a C-C is 1.54 Å. Because the product bond lengths are not the same the position of the transition state (early or late) cannot be defined. When looking at the through space distances both structures have steric hindrance and this is numerically explained by the fact that the through space distances are smaller than the Van der Waals distance of 3.20 Å.[6] The exo transition state through space distance is greater than the endo transition state suggesting that the steric repulsion is lower in the exo transition state structure and consequently more thermodynamically favoured.
Exo and Endo Activation Energies
Already knowing that the endo product is kinetically favoured, this can be explianed further by looking at the activation energy values for the endo and exo structure which if correct should show a lower energy of activation for the endo transition state structure. The values can be seen in the table below:
| Thermodynamic Value | Exo | Endo |
|---|---|---|
| Sum of electronic and thermal energies for the two fragments (a.u.) | -612.53459 | -612.53459 |
| Sum of electronic and thermal energies for the two transition states (a.u.) | -612.481358 | -612.488746 |
| Activation Energy (a.u.)) | 0.0531 | 0.04584 |
| Activation Energy (kCal mol-1) (3 d.p.) | 33.417 | 28.751 |
HOMO of the EXO transition state
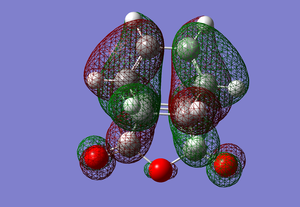HOMO of the ENDO transition state
The HOMO of the cyclohexadiene interacts with the LUMO of the maleic anhydride, this makes sense as both orbitals are antisymmetric.
The exo product is the one with a lower energy due to the stabilising interactions which are present in the exo product though the endo product has a lower energy of activation.
The endo product HOMO has a higher energy due to the repulsive interaction between the C=O π* orbital and the C=C π*. The exo does not have these repulsive interactions and so is favoured thermodynamically.
Conclusion
The use of computational chemistry in determining and predicting transition state structures has provided additional insight that spectroscopy and other methods cannot model. Because of this, it is possible to predict the likely pathway of chemical reactions by using optimisation and frequency analysis as well as energy calculations to determine key factors that govern the feasibility of reactions such as thermodynamic and kinetic data.
The project involved the computational study of two reactions - the Cope Rearrangement and the Diels-Alder Cycloaddition. Analysis has shown the likely pathways and the structures of the transition states based on the results from the calcualtions. The Cope Rearrangement underwent its reaction via a stabilised chair transition state.
The Diels-Alder cycloadditions indicated how orbital symmetry is conserved and how frontier molecular orbital theory can be used to model the transition state structures. The reaction between cis-butadiene and ethene proceeds via an envelope-like transition state explained by the dependence of the frontier orbitals. The reaction between maleic anhydride and cyclohexadiene was seen to form the endo structure under kinetic control. Once again this was explained by the secondary orbital overlap present in the endo structure (but not the exo).
References
- ↑ https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3.
- ↑ G. Schultz, I. Hrgittai, J. Mol. Struct., 1995, 346,63-69
- ↑ James H. Cooley and Richard Vaughan Williams; J. Chem. Educ., 1997, 74 (5), p 582
- ↑ Clayden, J.; Greeves, N.; Warren, S.; Wothers, P.; Organic Chemistry, 2011, Oxford University Press
- ↑ Keiji. Morokuma , Weston Thatcher. Borden , David A. Hrovat, J. Am. Chem. Soc., 1988, 110 (13), pp 4474–4475
- ↑ J. Bondi, A. (1964). "Van der Waals Volumes and Radii". J. Phys. Chem. 68 (3): 441–51.