Rep:Mod:tc1411syn

PART 1: Conformational analysis using Molecular Mechanics

The Dimerisation of Cyclopentadiene

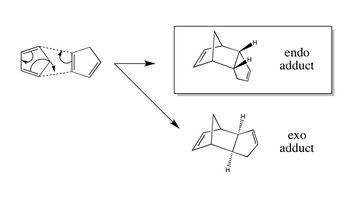
The dimerisation of cyclopentadiene occurs via a [π4s + π2s] cycloaddition and is an example of a Diels-Alder reaction. As the total electron count is 6, which fits the 4n+2 rule, the thermal reaction should proceed suprafacially via a Huckel transition state. Depending on the orientation of the reactants relative to each other in the transition state, it can be seen that two different products can be obtained where the exo adduct is the so-called thermodynamic product and the endo adduct is the kinetic product. In literature, it has been reported that to achieve equilibrium in the dimerisation of cyclopentadiene, extreme conditions are required and so, the reaction is usually under kinetic control. This leads to the preferential formation of the endo adduct which, though less stable than the exo adduct, is formed faster due to a combination of steric and secondary orbital overlap effects which stabilise its transition state.

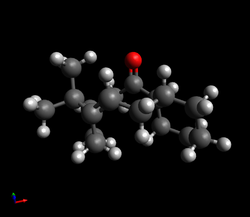
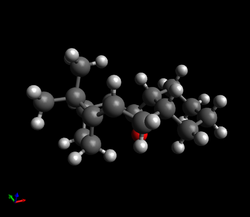
To confirm that the exo product is indeed the more thermodynamically stable, the geometries of the exo and endo product were optimised using the MMFF94s force field and the resulting energies were calculated. Using Avogadro, the total energy can be broken up into contributions from parameters such as the bond stretching energy, angle bending energy, torsional energy, Van der Waals energy and electrostatic energy - these parameters represent a deviation from ideality.

	Exo Dimer	Endo Dimer
(kcal/mol)
Total Energy	55.37364	58.19067
Total Bond Stretching Energy	3.54328	3.46793
Total Angle Bending Energy	30.77239	33.18941
Total Torsional Energy	-2.72512	-2.94947
Total Van der Waals Energy	12.79671	12.35868
Total Electrostatic Energy	13.01351	14.18449

As expected, the exo product was found to be 2.82 kcal/mol lower in energy than the endo product, meaning that is the more thermodynamically stable product. Analysis of the different contributions to the total energy shows that though the bond stretching energy, torsional energy and Van der Waals energy terms are similar in both adducts, the angle bending term differs by 2.42 kcal/mol; from this, it can be concluded that the differences in stability must be mainly due to the effects of angle strain.

Exo Dimer		Endo Dimer

[Green has been used for highlighting purposes - these atoms are still carbons]

The angle bending term describes the increase in energy as angles are bent away from their preferred values. Examination of the structures of the exo and endo products shows that the major difference in geometry is the orientation of the five-membered ring relative to the rest of the structure and therefore, it is the C-C-C angle between the two rings that is expected to differ most between the two - this angle has been highlighted above. In a molecule such as methane, where the carbon is sp3 hybridised, a tetrahedral geometry is observed in which the bond angles are 109.5°. However, in this case, though the carbon atom labelled green is also expected to be sp3 hybridised, the C-C-C bond angle deviates from the ideal angle of 109.5° due to the presence of the rings. For the exo product, the angle is 115.6° whilst for the endo product, the angle is 118.6°; the deviation from 109.5° is clearly larger for the endo product, leading to an increase in energy and making it less thermodynamically stable. As the endo product is less thermodynamically stable than the exo product but is the sole product that is observed during the dimerisation of cyclopentadiene, the reaction must be under kinetic control. This means that the endo transition state is expected to be more stable than the exo transition state, leading to a faster formation of the endo product relative to the exo product.

Hydrogenation of the Cyclopentadiene Dimer

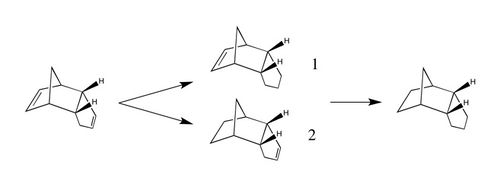
The hydrogenation of dicyclopentadiene to tetrahydrodicyclopentadiene has been found to proceed in a stepwise fashion; in other words, the two double bonds are not hydrogenated at the same time. Instead, as shown in the reaction scheme below, one of the double bonds is hydrogenated before the other, leading to a dihydro derivative being formed before the desired product, tetrahydrodicyclopentadiene, is obtained:

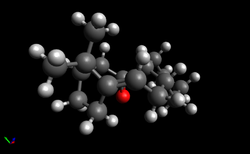
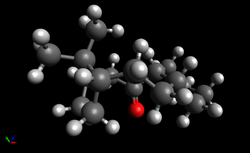
As there are two double bonds, the reaction can proceed via two different reaction paths: one in which the dihydro derivative (1) is formed and one in which the dihydro derivative (2) is formed. To determine which dihydro derivative is most thermodynamically stable and therefore the most likely to form if the reaction is under thermodynamic control, the geometries of (1) and (2) were optimised using the MMFF94s force field and the resulting energies were obtained:

	Product 1	Product 2
(kcal/mol)
Total Energy	50.72281	41.25749
Total Bond Stretching Energy	3.30830	2.82301
Total Angle Bending Energy	30.86050	24.68572
Total Torsional Energy	0.06397	-0.37807
Total Van der Waals Energy	13.28036	10.63668
Total Electrostatic Energy	5.12096	5.14702

Dihydro derivative (2) was found to be 9.47 kcal/mol lower in energy than dihydro derivative (1), meaning that it is more thermodynamically stable. Though the bond stretching energy, torsional energy and electrostatic energy terms are similar for both products, the angle bending term differs by 6.17 kcal/mol and the Van der Waals term differs by 2.64 kcal/mol - it is therefore these two terms that are the most significant and should be examined further. As stated above, the angle bending term describes the increase in energy as angles are bent away from their ideal value. Norbornane and norbornene rings are known to be highly strained as the C-C-C angle of the bridging CH2 is much smaller than the ideal angle of 109.5°; this means that both dihydro derivatives are expected to show large angle bending terms.

Product 1		Product 2

[Green/Blue have been used for highlighting purposes - these atoms are still carbons]

From the annotated diagram above, it can be seen that the C-C-C angle of the bridging CH2 is approximately 93.0° in both molecules, leading to strained rings and contributing to the large angle bending terms. However, as the size of this angle is almost identical in both dihydro derivatives, to understand why (1) has a higher angle bending term than (2), the angle highlighted in green must be examined in more detail. Due to the differing levels of saturation and hybridisation, the ideal C-C-C bond angle highlighted in green in (1) is 120.0° whilst in (2), it is 109.5°. The deviation between the calculated bond angle and ideal bond angle is approximately 13° in (1) and 7° in (2), meaning that (1) possesses more angle strain. This leads to an increase in the energy of (1) and so, as observed, (1) is expected to be less stable than (2). The Van der Waals term describes the increase in energy when two non-bonded atoms are in close proximity to each other and repel. In general, if the distance between two non-bonded atoms is smaller than the sum of their Van der Waals radii, they will repel - for two carbon atoms, this distance is approximately 3.40 Å. As the geometries of the two products are similar, only two key distances have been highlighted for further discussion:

Product 1		Product 2

[Green/Blue have been used for highlighting purposes - these atoms are still carbons]

The distances highlighted in green and blue are shorter than 3.40 Å in both molecules so products (1) and (2) are expected to possess a degree of Van der Waals repulsion. In product (1), the distance between the bridging CH2 and the carbon of the double bond [highlighted in green] is 2.30 Å whilst in product (2), the same distance is a longer 2.37 Å. On the other hand, in product (1), the distance highlighted in blue is 2.64 Å whilst in product (2), the presence of the double bond leads to a shortening of this distance to 2.61 Å. Although the presence of a double bond leads to greater Van der Waals repulsion between surrounding atoms for both molecules, the amount of Van der Waals repulsion is expected to be slightly greater for product (1), leading to an increase in its energy. However, as noted above, the main contribution to the higher energy of (1) relative to (2) is angle strain, rather than Van der Waals repulsion. Due to the reasons discussed, dihydro derivative (1) is less stable than dihydro derivative (2). Remembering that the reactant in the first hydrogenation, the endo cyclopentadiene dimer, has a calculated energy of 243.5 kJ/mol, the energy difference between the reactant and product (1) is 31.2 kJ/mol but 70.8 kJ/mol for product (2); in other words, forming product (2) is more thermodynamically favourable than forming (1). This means that if the reaction is under thermodynamic control - in which the more stable product predominates - the first hydrogenation will give the dihydro derivative (2) over (1).

Atropisomerism in an Intermediate related to the Synthesis of Taxol

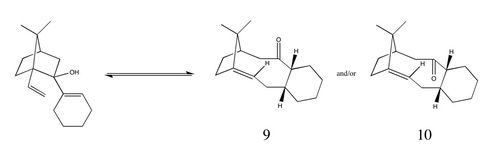
One of the key intermediates, (9) or (10), in the synthesis of Taxol as proposed by Paquette shows atropisomerism. This arises as the fused rings hinder rotation around the single C-C bonds, leading to the conformers (9) and (10) being isolable stereoisomers. The difference between the two stereoisomers is the position of the carbonyl group - in (9), the carbonyl group points in the same direction as the CMe2 bridge whilst in (10), the carbonyl group points in the opposite direction.

As shown above, stereoisomers (9) and (10) are thought to form from a reversible anionic oxy-Cope rearrangement of a carbinol. This rearrangement is reversible and therefore, given enough time, the most thermodynamically stable stereoisomer will dominate and either (9) or (10) will be obtained, not both. In order to determine which stereoisomer is the most stable, the geometries of (9) and (10) were optimised using the MMFF94s force field and the resulting energies were calculated. For bicyclic systems, it has been reported that the larger ring tends to adapt its geometry in order to favour the most stable conformation of the smaller ring, provided that the smaller ring is made up of at least six atoms. In this case, the smaller ring is a cyclohexane ring which is known to have four isolable conformers - two chairs and two twist-boats - so having the cyclohexane ring in (9) and (10) in these conformations is expected to give the lowest energies.

	Chair (1)	Chair (2)	Twist-Boat (1)	Twist-Boat (2)
ATROPISOMER 9
Total Energy (kcal/mol)	70.54272	82.69267	77.91792	94.20779

	Chair (1)	Chair (2)	Twist-Boat (1)	Twist-Boat (2)
ATROPISOMER 10
Total Energy	74.94115	60.55674	66.31670	65.69184

In both cases, the lowest energy conformer - chair (1) for atropisomer (9) and chair (2) for atropisomer (10) - has the cyclohexane ring in a chair conformer. This is as expected as the chair conformation is the most stable conformation for cyclohexane due to minimised torsional strain. If these two conformations are compared, as in the table below, it can be seen that isomer (10) is lower in energy than isomer (9) by 9.99 kcal/mol:

	Isomer 9 (Chair 1)	Isomer 10 (Chair 2)
(kcal/mol)
Total Energy	70.54272	60.55674
Total Bond Stretching Energy	7.67589	7.59047
Total Angle Bending Energy	28.29867	18.79727
Total Torsional Energy	0.25810	0.19831
Total Van der Waals Energy	33.11040	33.32445
Total Electrostatic Energy	0.30388	-0.05609

Analysis of the different contributions to the total energy shows that though the bond stretching energy, torsional energy, Van der Waals energy and electrostatic energy terms are similar for both isomers, the angle bending energy term differs by 9.50 kcal/mol. This implies that the bond angles in (9) deviate further from ideality than in (10), leading to it having a higher total energy.

Atropisomer (9)		Atropisomer (10)

[Green/Blue have been used for highlighting purposes - these atoms are still carbons]

As for the norbornane ring discussed earlier, the bond angle of the bridging CMe2, highlighted in green, is expected to contribute to the angle bending term. For both isomers, this bond angle is approximately 96°, a much smaller angle than the ideal angle of 109.5°, leading to significant angle strain in the structure. However, to understand why the angle bending term for (9) is much higher than for (10), it is the angle highlighted in blue that should be examined. For isomer (9), this angle is 123.0° whilst for isomer (10), this angle is a smaller 118.2°. Both of these angles deviate greatly from the ideal 109.5° but the deviation is greater for isomer (9), presumably due to the carbonyl oxygen and the hydrogen of the bridging methyl group not wanting to be in close proximity to each other. This means that the angle strain is higher in atropisomer (9) and so, it is atropisomer (10) that is more thermodynamically stable and the one that is formed if the reaction is under thermodynamic control.

Hyperstable Olefins

Subsequent functionalisation of the alkene in (10) was found to occur at an abnormally slow rate, going against Bredt's rule which states that double bonds at ring junctions are unfavourable and should therefore lead to increased reactivity. In fact, Bredt's rule was proved to be incorrect for larger rings and in 1970, Wiseman observed that bridgehead olefins could be isolated if they were contained in a trans cycloalkene unit composed of eight or more atoms. Compound (10) is actually an example of a 'hyperstable' olefin, an olefin that is less strained than its parent hydrocarbon and that shows decreased reactivity due to the double bond being located at the bridgehead. The unusual stability of hyperstable olefins relative to their parent hydrocarbons cannot be explained by considering factors such as steric hindrance and π-bond energy but is instead thought to be due to the differing hybridisations of the bridgehead carbon. If the energies of (10) and its saturated counterpart (11) are compared:

	10 (Unsaturated)	11 (Saturated)
(kcal/mol)
Total Energy	60.55674	71.44617
Total Bond Stretching Energy	7.59047	6.60799
Total Angle Bending Energy	18.79727	24.77597
Total Torsional Energy	0.19831	8.34933
Total Van der Waals Energy	33.32445	31.21382
Total Electrostatic Energy	-0.05609	0.00000

As predicted, (10) is more stable than (11) by approximately 10.9 kcal/mol. Analysis of the contributions to the total energy show that the main reasons for the higher energy of (11) relative to (10) are increased angle bending energy and torsional energy; however, Kim has stated that differences in torsional energy do not contribute much towards hyperstability and therefore, in this discussion, it is the difference in angle strain that has been focused on. It has been reported in previous works that introducing a bridgehead double bond into a medium-sized ring leads to flattening of the bridgehead position and relief of angle-strain in the rest of the ring, making the structure more stable. In order to investigate whether this can be used to explain the unusual stability of (10) relative to (11), the key angles have been highlighted:

(10)		(11)

[Green has been used for highlighting purposes - these atoms are still carbons]

Although the angle highlighted in green is approximately 122.0° for both (10) and (11), an angle of this size leads to much greater angle strain in the ring of (11) than in (10). This is because introducing a double bond leads to sp2 hybridisation of the carbons rather than sp3 and the ideal bond angle increases from 109.5° to 120.0°. The deviation away from the ideal C-C-C bond angle is therefore just 3.7° for (10) but for (11), it is a much greater 12.2°. Similar observations are found for the other angles around the double bond, meaning that the ring in the bridgehead olefin (10) suffers much less angle strain than its parent hydrocarbon, giving it extra stability. The difference in hybridisation also leads to less unfavourable transannular interactions between the hydrogens indicated above. This is because a sp2 hybridised carbon has one less hydrogen than a sp3 carbon, meaning that the hydrogen can be positioned in a way that helps minimise transannular interactions; in (10), the distance between the hydrogens indicated is 0.255 nm whilst in (11), the same distance is a smaller 0.238 nm. The degree of transannular interactions in (11) is therefore expected to be higher than in (10), destabilising it. Thanks to reduced angle strain and unfavourable transannular interactions in the larger ring, molecule (10) not expected to be very reactive. It is therefore not too surprising that functionalisation of the alkene occurs at a slow rate.

Spectroscopy of an intermediate related to the synthesis of Taxol

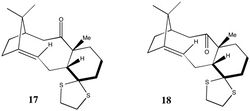
Molecules (17) and (18) shown to the left are derivatives of molecules (9) and (10) discussed above. Remembering that for bicyclic systems, the larger ring adapts its geometry so that the smaller ring can be in its most stable conformation, the cyclohexane ring in both (17) and (18) is expected to be in the chair conformation. As for (9) and (10), (18) should be more stable than compound (17) as the carbonyl group is pointing away from the bridging CMe2 and methyl group; however, to check that this is indeed the case, (17) and (18) were minimised using the MMFF94s force field and the resulting energies calculated.

	17	18
(kcal/mol)
Total Energy	104.35650	100.55273
Total Bond Stretching Energy	15.79879	15.07910
Total Angle Bending Energy	31.83391	30.56602
Total Torsional Energy	11.36667	9.83037
Total Van der Waals Energy	51.57951	49.60061
Total Electrostatic Energy	-7.56308	-6.06411

As expected, (18) is more stable than (17) by approximately 3.80 kcal/mol; however, as the structure of (17) prevents free rotation of the σ bonds, conformational isomerism between (17) and (18) does not occur readily at room temperature and instead, they exist as discrete atropisomers. This difference in stability can also be seen from the Gibbs free energies, where (17) has a higher energy than (18):

	17	18
Gibbs Free Energy (au)	-1651.445148	-1651.462140

¹H NMR Spectrum of (18)

To simulate the 1H NMR spectrum of (18), the minimised geometry from above was taken and reoptimised using DFT [density functional theory] methods at the B3LYP/6-31G(d,p) level of theory. The following result was obtained for the 1H NMR spectrum of (18) with deuterated benzene as the solvent:

		Computed			Experimental
		δ (ppm)	Integration		δ (ppm)	Integration
		5.97	s, 1H		5.21	m, 1H
		3.12	s, 2H		3.00-2.70	m, 6H
		2.95	s, 2H
		2.89	s, 1H
		2.80	s, 2H
					2.70-2.35	m, 4H
		2.67	s, 1H
		2.54	s, 2H
		2.43	s, 1H		2.20-1.70	m, 6H
		2.31	s, 1H
		1.98	s, 2H
		1.83	s, 2H
		1.53	s, 2H		1.58	s, 1H
					1.50-1.20	m, 3H
		1.34	s, 1H
		1.21	s, 1H
		1.40*	s, 3H		1.10	s, 3H
		1.27*	s, 3H		1.07	s, 3H
		1.13*	s, 3H		1.03	s, 3H

*When calculating the NMR, Gaussian does not account for fluxionality effects such as bond rotation. This means that the three hydrogens on each methyl group are treated separately and three distinct peaks are obtained, each with an integration of one. In the table above, the chemical shifts for the three hydrogens in each methyl group have been averaged to give one peak of integration 3H.

¹³C NMR Spectrum of (18)

The 13C NMR spectrum of (18) was simulated in the exact same way as for the 1H NMR spectrum above. The following result was obtained for the 13C NMR spectrum of (18) with deuterated benzene as the solvent:

		Computed		Experimental
		δ (ppm)		δ (ppm)
		211.92		211.42
		147.87		148.72
		120.12		120.90
		92.85		74.61
		65.94		60.53
		54.94		51.30
		54.76		50.94
		49.53		45.53
		48.03		43.28
		45.64		40.82
		44.02		38.73
		41.47		36.78
		38.51		35.47
		33.69		30.84
		32.47		30.00
		28.36		25.56
		26.50		25.35
		24.44		22.21
		24.00		21.39
		22.58		19.83

Comparison of Computed NMRs and Experimental NMRs

From the data above, it can be seen that the general trend in the chemical shifts of the protons and carbons of (18) are the same for both the computed NMR and the literature NMR; however, the values do not match up exactly and there is some deviation. In order to analyse the deviations more closely, the chemical shift values from above were used to form the following graphs:

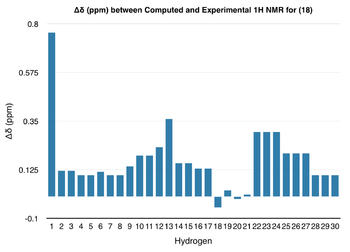
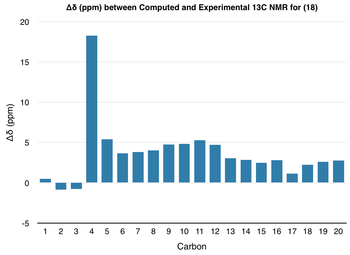
For both 1H NMR and 13C NMR spectra, the deviation in chemical shift is generally small. However, in the 1H NMR spectrum, the computed value of the most deshielded proton - corresponding to the hydrogen directly attached to the C=C double bond - is almost 0.80 ppm higher than the experimental value. On the other hand, in the 13C NMR spectrum, though the deviation for most of the peaks is less than +/- 5 ppm, the carbon attached to the two sulphur atoms shows a deviation of nearly 20 ppm. Although this deviation seems unusually high, as sulphur is a so-called 'heavy' element, corrections need to be made to the chemical shift of any carbons attached to it due to spin-orbit coupling errors. This means that the deviation, though significant, may not actually be as large as 20 ppm. As the method used to generate the NMR spectra is highly sensitive to different conformations and does not take into account fluxionality effects, deviations from literature can easily arise. Deviations could have also been caused by the computational method itself; though the B3LYP basis set has been shown to give reasonable results for the calculation of NMR spectra, during the optimisation of a molecule, various approximations are made to solve the Schrodinger equation [so that the structure of the molecule where the first derivative of the potential energy surface is zero can be obtained] and these approximations could be leading to inaccurate results.

PART 2: Analysis of the properties of the synthesised alkene epoxides

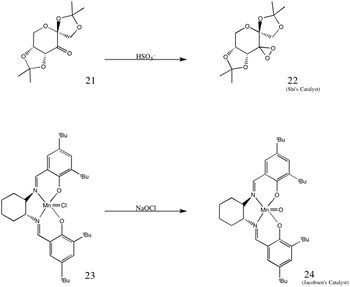
In experiment 1S, the Shi and Jacobsen catalysts were prepared and used to carry out an asymmetric epoxidation of trans-stilbene and β-methylstyrene. The structures of both catalysts are shown on the left, where (21) and (23) are the stable precursors to the active catalysts (22) and (24) respectively. In this section, investigation of the asymmetric epoxidations has been carried out in order to predict and rationalise the configuration of the resulting epoxide products. The structures of the starting alkenes, trans-stilbene and trans-β-methylstyrene, are as follows:

Crystal Structures of the Shi and Jacobsen Catalyst

The Cambridge crystal database was searched using Conquest in order to locate the crystal structures of the pre-catalysts (21) and (23). Key bond distances were then recorded using Mercury and have been reported below.

Shi's Catalyst

Originally, the anomeric effect was defined as the thermodynamic preference for polar groups bonded to the anomeric carbon of glycopyranosyl derivatives to be in axial positions; however, the definition is now more general and describes the preference for gauche conformations around the C-X bond in a Y-C-X-C system where X and Y are heteroatoms with lone pairs. In cyclic systems, it is thought that the anomeric effect arises from hyperconjugation: as illustrated in the diagram to the left, if the lone pair of a heteroatom is aligned antiperiplanar to a C-X bond, the orbital overlap is such that the lone pair can be donated into the σ*C-X orbital, lowering the overall energy of the system and leading to stabilisation. Another consequence of the anomeric effect is that the O(1)-C(2) bond is shortened whilst the C(2)-X(3) bond is lengthened.

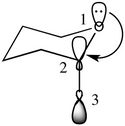
Shi's catalyst is a fructose-derived ketone that is an effective catalyst for the asymmetric epoxidation of trans- and trisubstituted alkenes. The enantioselectivity of epoxidation reactions with Shi's catalyst is thought to be due to steric effects between the dimethyl ketal groups and the substituents on the incoming alkene. Searching of the Cambridge crystal database resulted in two crystal structures for the Shi catalyst precursor (21) - NELQEA and NELQEA01 - and examination of the structures indicated that there might be anomeric interactions present. To determine whether this was indeed the case, the C-O bond distances for NELQEA were measured and recorded:

			C-O Bond Lengths (Å)
		C(4)-O(4)	1.395
		C(1)-O(1)	1.400
		C(2)-O(2)	1.403
		C(2)-O(6)	1.403
		C(10)-O(5)	1.409
		C(7)-O(1)	1.413
		C(5)-O(5)	1.416
		C(6)-O(6)	1.420
		C(10)-O(4)	1.439
		C(7)-O(2)	1.441

A typical bond length for the C-O bond in pyranoses and furanoses is 1.438 Å. As stated above, the anomeric effect causes a change in bond length so any C-O bond lengths that are significantly shorter/longer than this distance may indicate the presence of an anomeric interaction. If the cyclohexane ring is first examined, it can be seen that it is in the chair conformation, the most stable conformation for rings of this size. The most pronounced anomeric interaction occurs around carbons (10) and (7). If the carbon (10) centre is examined, it can be seen that the lone pair on O(5) can be aligned antiperiplanar to the C(10)-O(4) bond. This lone pair can be donated into the σ*C(10)-O(4) orbital, leading to a shortening of the C(10)-O(5) bond and a lengthening of the C(10)-O(4) bond as observed. The same occurs around carbon (7): the lone pair of O(1) can donate into the σ*C(7)-O(2) orbital as it is aligned in an antiperiplanar arrangement. If the O(6)-C(2) and C(2)-O(2) bonds are examined, it can be seen that there is a potential for an anomeric interaction here as the oxygen lone pair is aligned antiperiplanar to the C(2)-O(2) bond. The C(2)-O(2) and C(2)-O(6) bond lengths are the same, indicating that there is an anomeric effect going in both directions. This also explains why the C(2)-O(2) bond is orientated axial to the cyclohexane ring. Interestingly, both the C(2)-O(2) and C(2)-O(6) bonds are shorter than would be expected; this might be due to an inductive effect from the carbonyl group.

Jacobsen's Catalyst

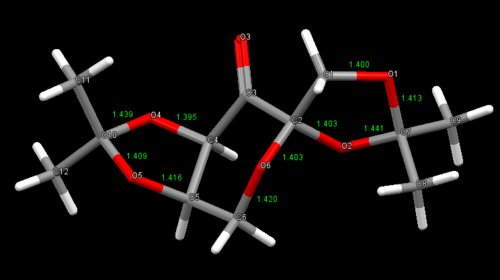
Jacobsen's catalyst is a manganese-containing complex that is an effective catalyst for the asymmetric epoxidation of cis-olefins. In order to investigate the structure of Jacobsen's catalyst in more detail, the crystal structure of its precursor (23) was located by searching the Cambridge crystal database. This yielded two crystal structures for (23), TOVNIB01 and TOVNIB02:

			TOVNIB01: H--H Distance (Å)
		H(18)-H(50)	2.694
		H(19)-H(52)	2.975
		H(20)-H(49)	2.963
		H(22)-H(47)	2.421
			TOVNIB02: H--H Distance (Å)
		H(18)-H(50)	2.625
		H(19)-H(52)	3.287
		H(20)-H(49)	2.363
		H(22)-H(47)	3.003

For two hydrogen atoms, the sum of the Van der Waals radii is 2.40 Å. As the hydrogens of the t-butyl groups indicated above for both crystal structures are separated by a distance greater than 2.40 Å, there must be attractive Van der Waals forces here. This leads to the t-butyl groups being pulled closer together, forcing the structure to be non-planar. In addition to this, the large steric bulk of the t-butyl groups means that it is sterically unfavourable for the alkene to approach from this end of the complex and instead, the alkene is more likely to approach over the diimine bridge - this supports previous work by Jacobsen and Katsuki. The main difference between TOVNIB01 and TOVNIB02 is that in the former, the methyl groups of the t-butyl are staggered whilst in the latter, the methyl groups are eclipsed. Staggering the methyl groups appears to shorten the H--H through-space distances, leading to greater attractive Van der Waals forces between the t-butyl groups. In addition to this, whilst all the H--H through-space distances in TOVNIB01 are greater than 2.40 Å, the through-space distance between H(20)-H(49) in TOVNIB02 is 2.36 Å, meaning that there is a degree of repulsion here; however, as the distance is only slightly shorter than 2.40 Å, this repulsion is expected to be weak. As the t-butyl groups in TOVNIB01 are closer together than in TOVNIB02, the structure of the complex is expected to be less planar than TOVNIB02. This can be seen below:

TOVNIB01		TOVNIB02

Though the angle indicated for TOVNIB01 is slightly smaller than for TOVNIB02, both angles are approximately 154°, indicating that both complexes are not planar. Instead, the complex appears to be concaved and so, one face of the molecule is more sterically hindered than the other. This makes attack from the top face of the molecule [where the Mn=O is pointing upwards] more favourable than if it was completely planar.

Assigning the Absolute Configuration of the Products

In experiment 1S, the epoxidation of trans-stilbene and trans-β-methylstyrene was carried out using the Shi and Jacobsen catalysts. For the epoxidation of trans-stilbene, a mixture of (S,S) and (R,R)-stilbene oxide is expected whilst for the epoxidation of trans-methylstyrene oxide, a mixture of (R,R) and (S,S)-methylstyrene oxide is expected. The ratio of one enantiomer to the other depends on the selectivity of the catalyst used and the reasons for why a particular enantiomer might be favoured will be investigated in this section.

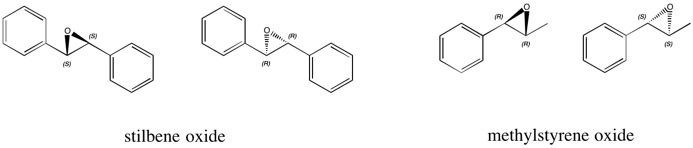
To start, the 1H NMR and 13C NMR spectra of stilbene oxide and methylstyrene oxide were simulated. This was done in the same way as for Taxol, by first minimising the geometry using the MMFF94s forcefield and then reoptimising the geometry using DFT methods at the B3LYP/6-31G(d,p) level of theory. Once this was done, their optical rotations were calculated and compared to literature values in order to determine which enantiomer had been modelled.

Stilbene Oxide

NMR Spectra of Stilbene Oxide

¹H NMR of Stilbene Oxide

		Computed			Experimental
		δ (ppm)	Integration		δ (ppm)	Integration
		7.57	s, 2H		7.45-7.26	m, 10H
		7.48	s, 8H
		3.54	s, 2H		3.86	s, 2H

¹³C NMR Spectrum of Stilbene Oxide

		Computed δ (ppm)		Experimental δ (ppm)
		134.09		136.99
		124.21		128.44
		123.52		128.44
		123.21		128.19
		123.08		128.19
		118.26		125.40
		66.42		62.81

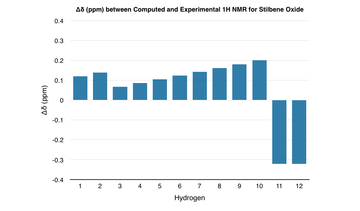
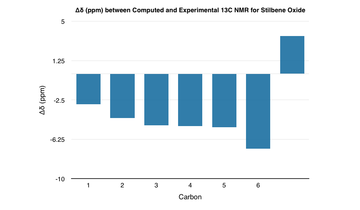
The computed 1H and 13C NMR spectra agree closely with the literature - the greatest deviation in the 1H NMR is approximately 0.3 ppm whilst for the 13C NMR, it is approximately 7.0 ppm. Any deviations in the values most likely come from differences in the conformation of the molecule or the computational method itself.

Calculated Chiroptical Properties of trans-Stilbene Oxide

The optical rotation of trans-stilbene oxide was calculated at 589 nm using the B3LYP method, 6-31++g(2df,p) basis set and a chloroform solvent model. The literature values for the optical rotation of (R,R) and (S,S)-stilbene oxide in chloroform at 589 nm have been tabulated below for comparison:

	(R,R)	(S,S)
Experimental	250.80°	-249.00°
Computed	297.78°	-297.90°

The computed value for the optical rotation of stilbene oxide shows good agreement with literature, indicating that the computational methods used were accurate.

Methylstyrene Oxide

NMR Spectra of Methylstyrene Oxide

¹H NMR of Methylstyrene Oxide

		Computed			Experimental
		δ (ppm)	Integration		δ (ppm)	Integration
		7.49	s, 3H		7.40-7.20	m, 5H
		7.42	s, 1H
		7.31	s, 1H
		3.41	s, 1H		3.57	d, 1H
		2.77	s, 1H		3.03	qd, 1H
		1.33*	s, 3H		1.45	d, 3H

*When calculating the NMR, Gaussian does not account for fluxionality effects such as bond rotation. This means that the three hydrogens on the methyl group are treated separately and three distinct peaks are obtained, each with an integration of one. In the table above, the chemical shifts for the three hydrogens have been averaged to give one peak of integration 3H.

¹³C NMR Spectrum of Methylstyrene Oxide

		Computed δ (ppm)		Experimental δ (ppm)
		134.98		137.90
		124.07		128.40
		123.33
		122.80		128.00
		122.73		125.5
		118.49
		62.32		59.50
		60.58		59.00
		18.84		18.00

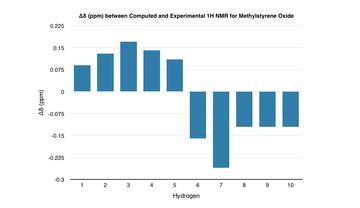
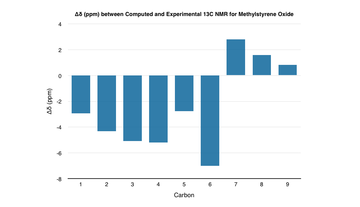
The computed 1H and 13C NMR spectra agree closely with the literature - the greatest deviation in the1H NMR is approximately 0.3 ppm whilst for the 13C NMR, it is approximately 7.0 ppm. Any deviations in the values most likely come from differences in the conformation of the molecule or the computational method itself.

Calculated Chiroptical Properties of Methylstyrene Oxide

The optical rotation of methylstyrene oxide was calculated at 589 nm using the B3LYP method, 6-31++g(2df,p) basis set and a chloroform solvent model. The literature values for the optical rotation of (R,R) and (S,S)-methylstyrene oxide in chloroform at 589 nm have been tabulated below for comparison:

	(R,R)	(S,S)
Experimental	47.00°	-43.6°
Computed	46.88°	-46.77°

The computed optical rotations for methylstyrene oxide show good agreement with literature, indicating that the computational methods used were accurate.

Using the Calculated Properties of the Transition State for the Reaction

In order to check the enantiomeric assignment carried out above using the computed optical rotations, the relative free energies of the transition state should be analysed.

The Transition State for the Shi Epoxidation of Stilbene

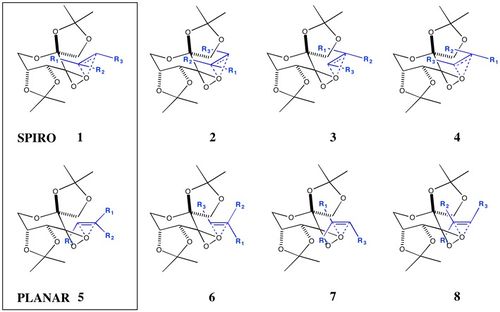
For epoxidation reactions carried out with Shi's catalyst, there are eight possible transition states, four spiro transition states and four planar transition states. Which one occurs depends on whether the Re or Si face of the alkene is reacted, which dioxirane oxygen is transferred and how the phenyl group of the alkene is orientated relative to the catalyst. From examination of the transition states shown on the left, it can be seen that the eight different transition states are not equally likely to form. Transition states 2-4 and 6-8 are unfavourable due to steric interactions between the substituents on the alkene and the dioxolane groups, leaving transition states 1 and 5 as the most sterically favourable. These transition states lead to epoxide products of opposite configurations and therefore, a greater enantiomeric excess is obtained if the conditions of the reaction are such that one transition state is significantly more favoured than the other. However, due to the effects of secondary orbital interactions discussed below, the epoxidation of trans/trisubstituted alkenes proceeds mainly through spiro transition state 1 with high enantiomeric excess.

For a disubstituted alkene like stilbene, spiro transition states 1 and 4 are equivalent, spiro transition states 2 and 3 are equivalent, planar transition states 5 and 8 are equivalent and planar transition states 6 and 7 are equivalent. There are therefore only four distinct transition states remaining, spiro 1 and 2 and planar 5 and 6. Using the same steric arguments as above, transition states 2 and 6 are likely to be higher in energy as they are more sterically unfavourable. To investigate this further, the two lowest energy transition states have been shown below for further discussion:

	(R,R) Transition State		(S,S) Transition State
Gibbs Free Energy (au)	-1534.700037		-1534.693818

From the animations above, it can be seen that in both transition states, the stilbene molecule is orientated such that unfavourable steric interactions between its phenyl substituent and the dioxolane groups on the catalyst are minimised. The (R,R) transition state is similar to spiro transition state 1 whilst the (S,S) transition state is similar to planar transition state 5. From the Gibbs free energy of the transition states, the (R,R) transition state is found to be lower in energy than the (S,S) transition state, meaning that the (R,R) enantiomer will be formed in excess. Remembering that ΔG = -RTlnK, K is calculated to be 0.00137, giving an enantiomeric excess of 99.7%. This agrees with the literature, where an enantiomeric excess of 98.0% has been reported towards the (R,R) enantiomer for the epoxidation of stilbene with Shi's catalyst.

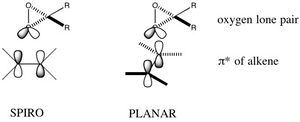
The reason why the spiro transition state is favoured over the planar transition state is thought to be due to a secondary orbital stabilising interaction between the oxygen lone pair of the dioxirane on the catalyst and the π* orbital of the alkene. This secondary orbital interaction is only present in the spiro geometry as shown to the left. It should also be noted that higher enantiomeric excesses will be obtained for alkenes with conjugating substituents as these lower the energy of the π* orbital, increasing the effect of secondary orbital interactions in the spiro transition state.

The Transition State for the Jacobsen Epoxidation of cis-β-methylstyrene

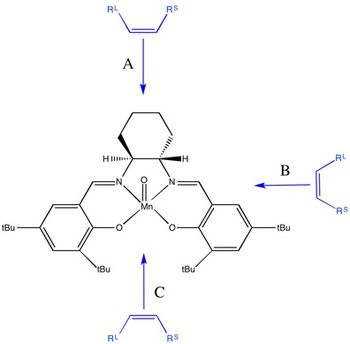
Alkene epoxidation reactions with Jacobsen's catalyst can go via four possible transition states, depending on whether the (R,S) or (S,R) enantiomer is formed and the orientation of the alkene with respect to the catalyst. There have been various approach trajectories proposed to explain the degree of enantioselectivity obtained with Jacobsen's catalyst, many of which involve a 'side-on' approach by the alkene to the metal as this allows favourable orbital overlap. In the diagram to the left, three of these 'side-on' approaches have been illustrated. In 1991, Jacobsen et al. proposed that the trajectory of approach was (A), where the alkene approached over the diimine bridge, as trajectory (B) and (C) were thought to be sterically unfavourable due to the presence of large, t-butyl groups. However, later work by Katsuki et al. argued that approach (A) was not the correct approach as it could not account for observations such as the unusually high enantiomeric excess observed with cis- alkenes and the effects of chirality at the 3,3'-positions. Instead, they proposed that since there was evidence that the salen ligand was in a stepped conformation [and not completely planar], the t-butyl groups would not sterically block trajectory (B) and that this was, in fact, the correct trajectory. This was supported by computational work by H. Jacobsen and Cavallo.

As the Jacobsen catalyst is known to work best for cis-alkenes, to get some further insight into the transition state of the Jacobsen-catalysed epoxidation, the two lowest energy transition states for the epoxidation with cis-β-methylstyrene were located:

	(S,R) Transition State		(R,S) Transition State
Gibbs Free Energy (au)	-3383.259559		-3383.251060

From the animations above, it can be seen that as proposed by Katsuki, the cis-β-methylstyrene molecule appears to have approached via a trajectory between the t-butyl groups and the diimine bridge. This is possible as the complex is not planar, meaning that the t-butyl groups are not as sterically hindering as might be expected. The (S,R) transition state is found to be lower in energy than the (R,S) transition state, meaning that the (S,R) enantiomer will be formed in excess. If the enantiomeric excess for this reaction is calculated in the same way as for the Shi catalyst above, a value of 0.000123 is obtained for K, giving an enantiomeric excess of 99.9%. In literature, the enantiomeric excess has been reported to be 92.0%, showing relatively good agreement with the computed value.

Investigating the Non-Covalent Interactions and Electronic Topology in the Active Site of the Reaction Transition State

According to Hohenberg-Kohn theorem, the ground state properties of a system is a consequence of its electron density. As chemical reactions lead to a redistribution of electron density, examining the electron density of a system gives an insight into the electron structure and reactivity of molecules. Two complementary methods have been developed to do this - QTAIM and NCI. The QTAIM [Quantum Theory of Atoms in Molecules] theory provides a spatial topological decomposition of electron density and makes it possible to relate topological properties of the electron density with structural properties of the system such as bonds. It does this by first identifying the atomic positions [the areas where the electron density is at a maximum] and then defining the bonds as the saddle points between them; these saddle points, also known as bond critical points, show minima in the bonding direction but maxima in all other directions. In contrast to QTAIM, the NCI [Non-Covalent Interactions] index does not look at the local values of electron density but instead, the electron density gradient. Regions where the electron density gradient is low represent regions where non-covalent interactions are likely to occur. To explore the transition state of the Shi epoxidation of trans-stilbene further, a NCI and QTAIM analysis was carried out on the lowest energy transition state. As discussed above, this is the spiro geometry (R,R)-transition state.

NCI		QTAIM
Orbital

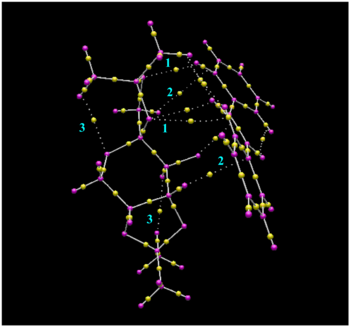
Examination of the NCI shows that there is a considerable amount of weakly attracting non-covalent interactions [green] between the catalyst and the alkene which help to stabilise the transition state. Using the QTAIM image, it can be seen that these interactions are made up of weak non-covalent interactions between the dioxolane oxygens on the catalyst and the hydrogens of the alkene (1), as well as weak non-covalent interactions between the hydrogens of the catalyst and the carbons of the phenyl groups of stilbene (2). The interactions between the dioxolane oxygens on the catalyst and the hydrogens of the alkene are likely to be hydrogen bonding-type interactions (1) whilst the interactions between the hydrogens of the catalyst and the carbons of the phenyl groups (2) are likely to be caused by dispersion forces. From the QTAIM image, it can also be seen that there are non-covalent interactions between the hydrogens and dioxolane oxygens of the catalyst (3). These interactions are weakly attractive, as seen from the NCI, and presumably help to stabilise the dioxolane rings which have strongly repulsive regions in the centre. In addition to this, these attractive interactions may also be contributing to the preferred conformation of the catalyst and may therefore be having some effect on its selectivity. Interestingly, the position of the bond critical point for the non-covalent interactions between the dioxolane oxygens on the catalyst and the hydrogens of the alkene seem to be in the middle of the two atoms (1). However, on closer inspection, they are, in fact, slightly nearer to the hydrogen atoms. The position of the bond critical point on the bond path reflects the polarity of the bond; if A is more electronegative than B in the bond A-B, the bond critical point will be found nearer to B. It therefore makes sense that the bond critical point is found nearer to the hydrogens as the oxygens are more electronegative, pulling electron density away. However, as the bond critical points are almost in the middle of the two atoms, the polarisation is weak; this is what would be expected as the interactions are not bonds but non-covalent interactions. The same result is obtained if the non-covalent interactions between the hydrogens of the catalyst and the carbons of the phenyl groups of the alkene are examined (2); the bond critical points are found near the middle, but slightly closer to the hydrogens. This indicates that the non-covalent interactions are slightly polarised towards the more electronegative carbon atom. As discussed above, the main reason why the transition state shown above is the most stable out of the possible eight is because of steric effects - the orientation of the alkene in this transition state is such that steric clashes between the substituents on the alkene and the dioxolane group of the catalyst are reduced. However, from studying the electron density of the system, it can be seen that due to the number of attractive non-covalent interactions present between the catalyst and the alkene pictured above, the alkene would be expected to approach from the side of the catalyst where the dioxirane is formed. In addition to this, the epoxidation with cis-stilbene might be expected to occur slower and with less selectivity as one of the phenyl groups of stilbene would be pointing away from the catalyst, leading to a decrease in the number of attractive non-covalent interactions that not only stabilise the transition state but help to direct the alkene into position. It should also be noted that there is thought to be a secondary orbital interaction between the non-bonding lone pair of the dioxirane oxygen and the π* of the alkene which is only present in the spiro geometry. Alkenes with conjugating groups like stilbene are therefore expected to show high enantiomeric excesses as the π* of the alkene is lowered, making these secondary orbital interactions more pronounced and the spiro transition state much more favourable than the planar transition state.

Suggesting New Candidates for Investigation

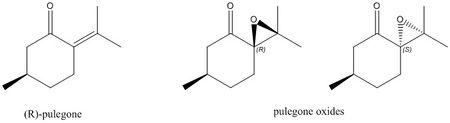
In general, the absolute configuration of a compound can only be successfully determined if the magnitude of its optical rotation is greater than |100|°. By searching the Reaxys database for epoxides with an experimentally-measured optical rotation of magnitude greater than |500|°, a potential new candidate for investigation has been found: pulegone. Pulegone is a component of the essential oils of plants such as peppermint and mint and is actually used commercially as a mint flavoring in food.

The experimentally-determined optical rotations of the (R) and (S) epoxide product at 324 nm and 327 nm respectively were found using Reaxys and have been shown below:

	(R)-enantiomer: [α]324	(S)-enantiomer: [α]327
Experimental	853.9°	-1177.9°

From the table above, it can be seen that both optical rotations have a magnitude that is greater than |500|° so it should be possible to use computational calculations to test the assignment. In addition to this, as the alkene, (R)-Pulegone, is available for purchase from Sigma Aldrich, the epoxide products are synthetically accessible and can be synthesised in the lab.