Rep:Mod:tb123

Module 3 - Stephanie Martinez

The Cope Rearrangement Tutorial

Optimising the Reactants and Products

Calculation Summary for 1,5-hexadiene (anti arrangement)

Calculation Summary for 1,5-hexadiene (gauche arrangement)

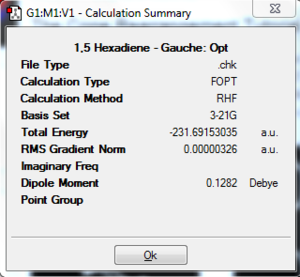
A molecule of 1,5-hexadiene (with an anti arrangement around the central carbon atoms, dihedral angle = 180.0°) has been created using Gaussview 3.0 and optimised using a Hartree-Fock Gaussian method and a 3-21G basis set. The resultant molecule had an energy of -231.6926 a.u.. The summary can be seen to the right. The point group is C₂. The same molecule was then modelled again, except this time with the four central carbon atoms in a gauche arrangement (dihedral angle = 0°). The same method and basis set was used in order to allow comparisons between energy calculations. The energy for this conformation is slightly less stable at -231.6915 a.u., and the point group is also the same: C₂.

1,5-Hexadiene - Anti

.....,..

1,5-Hexadiene - Gauche

.....,..

1,5 Hexadiene - Anti ........................

    1,5 Hexadiene - Gauche

Calculation Summary for Lowest Energy 1,5-Hexadiene (gauche)

HOMO for Lowest Energy 1,5-Hexadiene (gauche)

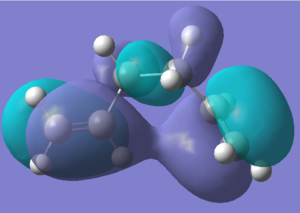
Initially, it was expected that due to steric clashes, the gauche conformation will be higher in energy, although this effect will not be very large because the alkene groups are relatively small. However, upon consultation with Appendix 1, it is apparent that actually it is a gauche conformation that is lowest in energy. This can be explained by a consideration of the molecular orbitals. The p orbital is close in energy and in physical proximity to the s* orbital of the nearby vinyl proton, thereby creating a small band gap and a stabilising overlap. The dihedral angle is 67.7°. According to appendix 1, this is gauche3. The conformers optimised above have been compared with the appendix and have been matched both by point group and by energy. They were anti1 and gauche4.

Calculation Summary for 1,5-Hexadiene: Ci symmetry

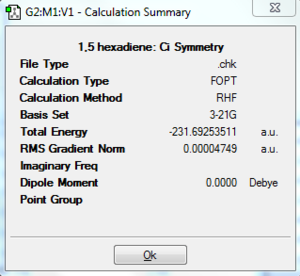
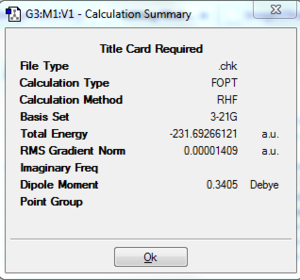
The angles in the anti arrangement above have been modified, and then the structure optimised, in order to produce an anti arrangement with the C_i point group. The final energy is -231.6925 a.u.; this is in agreement with the value given in appendix 1. Further optimisation was carried out by using a higher level method and basis set: B3LYP/6-31G*. This yielded a structure with an energy of -234.6117 a.u.. The use of a different method means that the energy cannot be compared directly, but a more negative value shows that the stability has increased.

1,5-Hexadiene; C Symmetry; (HF/3-21G)

.....,..

1,5-Hexadiene; C Symmetry; (B3LYP/6-31G*)

.....,..

....

1,5 Hexadiene (HF/3-21G)...............
    1,5 Hexadiene - (B3LYP/6-31G*)

Molecule Optimisation Method/Basis Set	C1-C2 Bond Length /Å	C2-C3 Bond Length /Å	C3-C4 Bond Length /Å	C1-C2-C3-C4 Dihedral Angle	C2-C3-C4-C5 Dihedral Angle
HF/3-21G	1.32	1.51	1.55	114.7	180.0
B3LYP/6-31G*	1.33	1.50	1.55	118.3	180.0

The table shows the difference between the optimised molecules. The bond lengths are extremely similar, and the major difference occurs in the dihedral angle, which has been increased by around four degrees. This small difference is apparent when looking at the structures, but the effect on the overall geometry is minimal.

Following on from this, a frequency analysis was performed on the optimised B3LYP/6-31G* structure using the same method. The analysis resulted in a list of 42 frequencies, all of which were positive, ranging from 74.52-3234.06 cm^-1. The log file has been viewed and the following data determined:
Sum of electronic and zero-point energies = -234.469 a.u.
Sum of electronic and thermal energies = -234.462 a.u.
Sum of electronic and thermal enthalpies = -234.461 a.u.
Sum of electronic and thermal free energies = -234.501 a.u.

The first value does not contain any thermal terms - it is the energy found at 0.00 K. The second value is the energy found at 298.15 K. The third value also has an RT term, while the final value also considers entropy.

Optimising the 'Chair' and 'Boat' Transition Structures

Calculation Summary for Allyl Fragment

Initial Guess for 'Chair' Structure

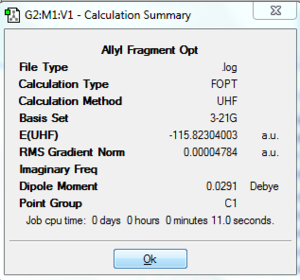
A CH₂CHCH₂ fragment has been drawn in Gaussview 3.0 and optimised using HF/3-21G theory. This was then copied twice in order to produce an approximation for the 'chair' transition structure (TS). The distance between the terminal ends of the allyl fragments was 2.19 Å in this initial model. Two different methods were attempted in order to optimise this structure.

Vibration: -818 cm^-1: Optimised Chair Structure

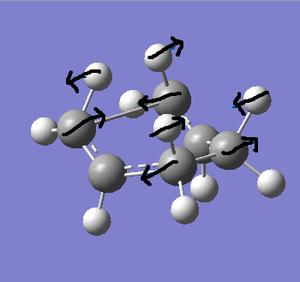
The first method involves computing the force constant matrix in the first step, then updating this as the optimisation continues. This was done by running a Gaussian Opt+Freq procedure, using HF/3-21G. Additional keywords of 'Opt=NoEigen' were also included. The optimisation completed successfully, returning one negative frequency of -818 cm^-1. The animation corresponding to this frequency relates to the Cope rearrangement, as can be seen by the carbon atoms coming together to form bonds, as the picture on the right shows.

The second method of transition state optimisation will now be attempted. This is the frozen coordinate method. It involves freezing the coordinate for the carbon atoms between which a bond will form during the reaction, and setting the distance as 2.2 Å. Apart from this restriction, it was run as a pure optimisation calculation under the same method as before. In the resulting structure, the distance was found as 2.20 Å exactly. In the chair found via method 1, this length was 2.02 Å.

The final part of producing a fully optimised transition state from the frozen coordinate method involves optimising the previously frozen bonds. An Opt+Freq method was run as before, to optimise to a transition state. In the resulting structure, the previously frozen bonds had shortened to 2.02 Å. A comparison between the TS structures as found via methods 1 and 2 revealed a remarkable similarity. To at least two decimal places, the bond lengths and angles in both fragments and between both fragments were exactly the same.

,,

.....,..

..

.....,..

Chair TS (Method 1) ........................

    Chair TS (Method 2)

Initial Failed Boat Optimisation

With the chair transition structure now optimised, the boat structure was tackled. The fully optimised 1,5-hexadiene molecule with C_i symmetry from earlier was used and set as both the reactant and the product, and optimisation attempted using the QST2 Opt+ Freq method. However, this method failed. The structure found looked like the chair structure, except this time the bond length between terminal carbon atoms was longer, at 3.05 Å. Instead of creating a boat, the optimisation procedure instead just translated one of the fragments. This is because of the geometry of the initial structures used. Improving the initial guesses will lead to a better optimisation.

Imaginary Frequency (-840 cm^-1): Optimised Boat Structure

The dihedral angle in the hexadiene fragments was changed to 0.0°, while the angles between the three 'inner' carbons were reduced to 100.0°. The optimisation procedure was then run again, as above. This time, a boat structure was successfully produced. Viewing the frequency analysis showed that only one imaginary frequency was found: -840 cm^-1.

Total Energy along IRC - Initial

The Intrinsic Reaction Coordinate Method (IRC) allows the minimum energy path to be followed from a transition structure to its local minimum on a potential energy surface. The IRC calculation was run on the optimised chair structure found from the second method above. The force constants were calculated once and the IRC only run in the forward direction (because the reaction coordinate is symmetrical). The number of points was initially taken as 50. However, the calculation had not fully completed after only 50 points and so a different strategy was attempted. The energy found from this method was -231.63 a.u..

Total Energy along IRC (Force Constants Calculated at each Step

Total Energy along IRC (N=100

The same process was attempted again, except this time the force constants were calculated at each step. The resultant structure had a slightly lower energy of -231.64 a.u.. A third method was also attempted, with the number of points increased to 100. The IRC energy plot (as shown to the right) shows that a minimum is clearly being approached - the final energy from this method was -231.69 a.u.. Using this value of energy and the geometry of the resultant product allows a comparison with Appendix 1 to be made -the product has a gauche2 conformation.

Both the final chair and boat optimised structures were further optimised using a higher method/basis set: B3LYP/6-31G*. The energies as found from this method are compared to the previous energies, found using the lower level method:

Method/Basis Set	Energy of Reactant/ Hartree	Energy of Chair TS / Hartree	Energy of Boat TS /Hartree
HF/3-21G	-231.69	-231.62	-231.60
B3LYP/6-31G*	-234.61	-234.56	-234.54

Although the geometry has not largely altered upon further optimisation, the energy has decreased by several hartrees. This indicates that although higher level optimisation is preferred because it gives improved energy totals, the structures vary only slightly, therefore it is more time efficient to find the correct structure using a lower level theory and then improve the method at the end.

The activation energy at 298.15 K can be calculated using the data from the optimised transition structures in comparison to the energy of the reactant. The energy has been converted using: 1 hartree = 627.509 kcal/mol.

Method/Basis Set	Activation Energy of Chair TS / kcal/mol	Activation Energy of Boat TS /kcal/mol
HF/3-21G	45.94	56.31
B3LYP/6-31G*	34.34	43.06

These values are close to the values recorded in Appendix 2. The overall pattern is exactly the same. When increasing to the higher level method/basis set, the activation energies decrease and get closer to the experimental values as found at 0 K. The boat transition structure has a higher energy, therefore more energy is needed for the reaction to proceed via this structure. The product as formed by the chair transition structure will be preferred.

The Diels-Alder Cycloaddition

Cis-butadiene: HOMO

Cis-butadiene: LUMO

Ethylene: HOMO

Ethylene: LUMO

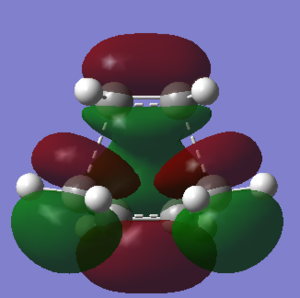
Butadiene and ethylene will undergo a Diels-Alder (DA) reaction to form cyclohexene. A molecule of cis-butadiene was created and optimised with the AM1 semi-empirical molecular orbital method. The MOs were plotted in the HOMO-LUMO region. As shown in the pictures, the HOMO is anti-symmetric with respect to the plane, while the LUMO is symmetric. A molecule of ethylene was also drawn and optimised. Its symmetry pattern is opposite to butadiene; the HOMO is symmetric, while the LUMO is anti-symmetric.

TS: HOMO

TS: LUMO

With this reactant fully optimised, reactants and the products were created and optimised in Gaussview. A QST2 semi-empirical AM1 Opt+Freq procedure was run. For the initial guess, a bond distance of 2.26 Å was assumed between the terminal carbons of adjacent fragments where a bond was to be formed. Upon optimisation, these bond lengths were found to be 2.12 Å. Typical carbon-carbon bond lengths are 154 pm for sp³ C, and 147 pm for sp² C. The length of the bond in the transition state therefore indicates that the fragments will still move closer together- what is seen in the transition structure is too long to be considered a chemical bond. The van der Waals radius for a typical carbon atom is 1.70 Å. In the transition structure, the bond length lies outside this - the atoms do not approach closer together due to electronic repulsion.

The HOMO and LUMO have been drawn for the resulting structure. With respect to the plane, the HOMO is anti-symmetric; the LUMO is symmetric. This is the same symmetry pattern as the butadiene fragment. The HOMO from the TS is formed by mixing the HOMO of butadiene with the LUMO of the ethylene fragment. This is allowed because they share the same symmetry - they are both anti-symmetric with respect to the plane.

Vibration corresponding to: Frequency = -956 cm^-1

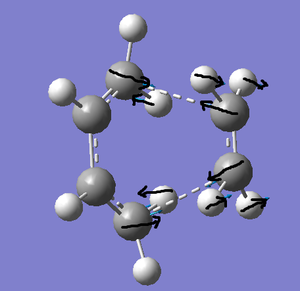
The TS yielded one imaginary frequency: at -956 cm^-1. This corresponded to the reaction pathway. The arrows indicate that the bond-forming atoms move in sync with each other - the bond forming process is synchronous. This is in contrast to the lowest positive frequency (147 cm^-1), where the bond forming process is asynchronous.

The Regioselectivity of the Diels-Alder Reaction

Exo TS

Endo TS

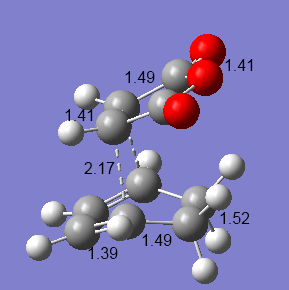
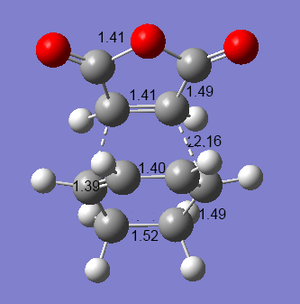
Maleic anhydride and cyclohexa-1,3-diene will undergo a Diels-Alder reaction to give two possible products - the endo adduct, or the exo adduct. The reaction is kinetically controlled so that the exo transition state will be higher in energy. The transition states were optimised using the semi-empirical AM1 method, using the Opt+Freq 'optimisation to a TS' (Berny) method, with the additional keyword: Opt=NoEigen.

Endo TS Energy = -0.0515 a.u. Exo TS Energy = -0.0504 a.u.

As expected, the energy of the exo transition structure is higher than for the endo structure. This explains why the endo- product is more commonly seen, even though the endo product appears to be the more hindered. The endo product is stabilised by the overlap of p orbitals on the dienophile substituents (carbonyls, in this case), with p orbitals on the diene. The structures can be seen in the accompanying diagrams. The carbon-carbon bond lengths have all been labelled in angstroms. The bond lengths are very similar in both structures, although the single bond to be formed is slightly longer in the exo structure.

Exo HOMO

Exo LUMO

Endo HOMO

Endo LUMO

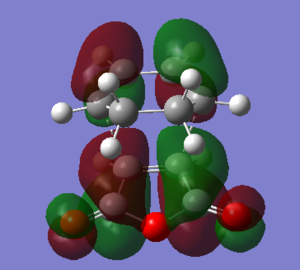
The overlap as mentioned above can be seen when looking at the MO pictures. The secondary orbital overlap effect is often responsible for facilitating the formation of the endo product over the exo product; however, in some molecules bearing sterically interactive substituents, steric destabilisation of the exo form is often a greater factor.