Rep:Mod:tah3

Cope Rearrangement

1,5 hexadiene can be optimised in 2 conformations – anti and syn.

The anti structure had an optimised energy of -231.69260237a.u. and a point group symmetry of C₂, when using the HF/3-21G method.

The syn conformation would be expected to have a higher energy due to the van der Waals repulsion from the methyl groups on the end as they are now on the same face as one another. Also the symmetry could be lower as there is no longer a C₂ axis.

After optimisation the energy was lower at -231.69166701a.u. The symmetry stayed at C₂.

As the gauche conformation had the lowest energy this is most likely to be the one to calculate the activation energy and enthalpies from.

Another version of the gauche was then optimised as this was to believed to have the lowest energy due to the end methyl groups pointing away from one another. The energy was lowered to -231.69153029a.u. and the point group remained at C₂.

The anti conformation is the same as the anti1 in appendix 1. The first gauche optimised is like gauche2 and the second structure which had the lower energy resembles gauche4, the energies are even the same!

The anti2 with the C_i symmetry was optimised and the energy was -231.69253530a.u. Compared with the appendix1 value of -231.69254 it is the same!

When the B3LYP/6-31G method was used the energy increased to -234.55971168a.u. this is compared with the appendix at -234.611710Hartree, this is slightly out but shows the significant change in energy due to the method used. However the structures have not changed and the symmetry is still C_i.

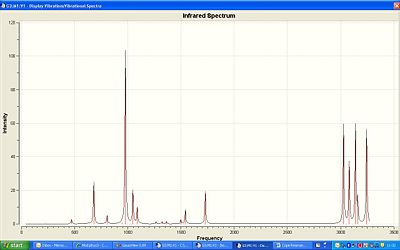
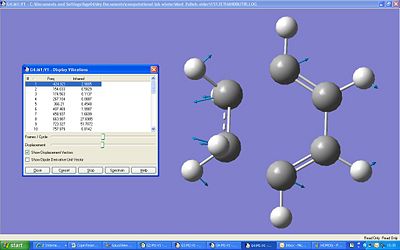
The vibrational frequency was optimised using the same method and basis set as before. The highest intensity peak comes from the CH₂ groups at the end stretching.

Sum of electronic and zero-point Energies (E = Eelec + ZPE )= -234.416225 Hartree

Sum of electronic and thermal Energies (E = E + Evib + Erot + Etrans )= -234.408939 Hartree

Sum of electronic and thermal Enthalpies (H = E + RT)= -234.407995 Hartree

Sum of electronic and thermal Free Energies (G = H - TS)= -234.447820 Hartree

Transition states

The chair transition state was calculated to have an energy of -231.6192246Hartree, and the vibrations showed an imaginary vibration at -817.942cm

^{-1.

After the bond forming distances were optimised the structure looked quite different with one of the distances between the new bond being formed being 4.39Å and the other at 1.55Å.

The structed which triend and failed at optimising came out looking like this. It has clearly not worked.

After the corrections were made the transition structure did resemble a boat and there was only one imaginary vibrations which was the transition state. This occoured at -840.376cm_-1.

The IRC ran initially and didn’t reach a minimum, so the calculation ran again and this time it was asked to always calculate force constants. After a long wait the IRC came out without a minimum againg, this is probably due to the transition structure not being close enough to the local minimum.

The Chair transition structure was re-optimised at the higher level of theory DFT-B3LYP with a basis set of 6-311G. The new energy calculated was -234.55868305Hartree. this is significantly different to the lower level of accuracy with an energy of -231.6192246Hartree, it shows that the level of theory really does change the outcome of the energy, even though the geometries look the same.
The activation energies for these calculations for the chair transition state =(234.55971168-234.55868305)x627.509kcal/mol = 0.65kcal/mol. This does not correlate with the value given in the text (33.5kcal/mol) this is due to the energy of the anti2 being out. The Sum of electronic and zero-point Energies=-234.415314 this is much the same as the appendix which is at -234.414919. the Sum of electronic and thermal Energies= -234.408058, appendix= -234.408998
The boat transition structure gave a new energy of -234.54639197, this is very close to the experimental value of -234.543093Hartree. The activation energy for this transition state is therefore = (234.54639197-234.55868305)x627.509 = 7.71kcal/mol, like the activation energy for the chair this number is far out that of the experimental data of 44kcal/mol. this is again due to the poor optimisation energy obtained from the anti2 structure. Sum of electronic and zero-point Energies=-234.401509, appendix = -234.402340, Sum of electronic and thermal Energies= -234.395827, appendix=-234.396006. Compared with the appendix values the results are very similar.

The Diels-Alder Cycloaddition
The reaction between butadiene and ethylene was studied to find out the transition structures.
The structure of cis-butadiene was optimised to an energy of 0.04880142Hartree. This was using a low level basis set of AM1. Also ethylene was optimised and produced an energy of 0.02619723Hartree.

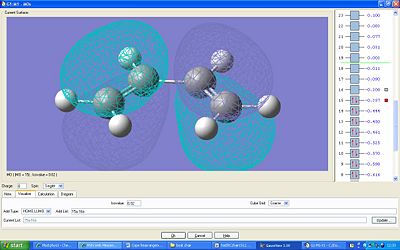
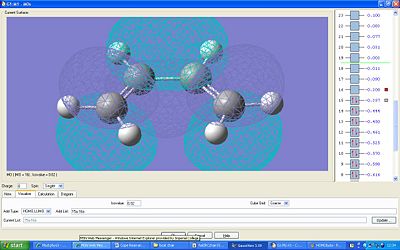
The HOMO and LUMO orbitals were also calculated. The HOMO is antisymmetric with respect to the plane and the LUMO is symmetric.

The orbitals of ethylene were calculated in order to see the overlap which occours during the diels alder reaction – the butadiene HOMO with the LUMO ethylene and visa versa:

Here the HOMO is symmetric and the LUMO is anti symmetric with respect to the plane.

The transition state was determined by first using the AM1 semi empirical method. The final energy was 0.24279934Hartree.
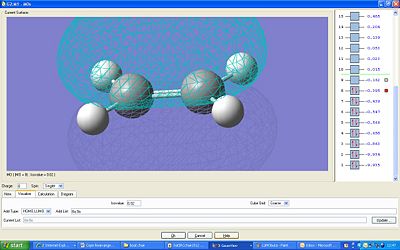
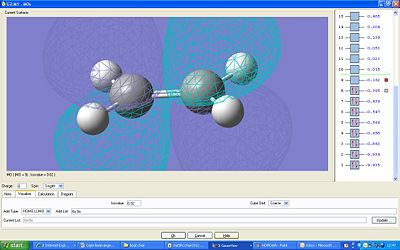
The HOMO and LUMO were plotted:

The LUMO is symmetric and the HOMO is antisymmetric. The MOs which have formed the HOMO looks to be both the π* orbitals of each
The bond lengths remained at 2.2Å which is what they were frozen at. Bond lengths¹ of c-c single bonds are 1.54Å and double bonds are shorter at 1.34Å. these are much shorter than the transition structure.
The IR gave an imaginary transition structure at -424.9cm^-1 it shows that the two bonds are synchronous. The next frequency at 154cm^-1 is asymmetric:

Maleic Anhydide
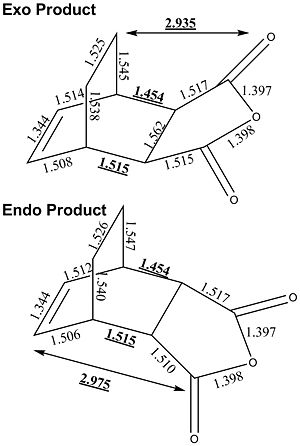
The endo product gave an energy of -0.15537394 Hartree and the exo of -0.15507193 Hartree.

Exo Product
Endo Product

The bond lengths of the products were compared. The new bonds formed were different lengths but the same lengths in each product, 1.454 and 1.515. The spacial difference between the bridge in the exo and the C=O bond is 2.935Å, but in the endo product the difference between the C=O and the double bond is greater at 2.975Å. this small difference can make a great difference to the reduction in energy from the reduced steric strain.

The HOMO of both the products are shown below:

In the exo product the orbitals are able to overlap with one another more than in the endo therefore this would be thought to be the more stable product. However it is not the one formed.

The secondary orbital overlap is preferred for the endo transition state due to more orbitals overlapping and therefore lowering the transition energy². This is the product formed.

References
http://www.science.uwaterloo.ca/~cchieh/cact/c120/bondel.html
Ian Flemming ‘’’Frontier Orbitals and Organic Chemical Reactions’’’ ‘’p107’’}