Rep:Mod:tah2

BCl₃ Molecule

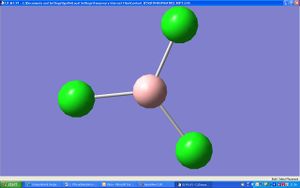
The triganol planar structure of BCl₃ was optimised using the FOPT type and calculation method of RB3LYP with the basis set as 3-21G. The type of file was a log file (.log).

The basis set was calculated to be D3_h which is expected for a triganol planar structure with 3 atoms the same. There was no dipole moment (0 Debye). The final energy was calculated as -1398.80a.u. This calculation only took 22.0s.

The optitmised B-Cl bond length was the same for each bond at 1.77503Å and the angle Cl-B-Cl was a perfect 120°.

Small Molecule(H₂O)

A molecule of H₂O was optimised. The type of file used was again ".log" the calculation type was FOPT and the method RB3LYP with a basis set of 3-21G. The optimsed energy of H₂O is -75.97a.u. H₂O has a point group of C2_v and a dipole of 2.2381D. The calculation completed in 23.0 seconds.

The coordinates of the molecule was as follows: O(0.000000, 0.000000, 0.122755) H(0.000000, 0.785462, -0.491020) H(0.000000, -0.785462, -0.491020)

The H-O bond length is 0.99683Å and the H-O-H angle is 103.991°

The Link to the structure is : http://hdl.handle.net/10042/to-1179

BH₃ Molecule

The optimised energy for BH₃ was -26.462a.u. The same methods were used as previous calculations. Once the frequency calculation was run the optimisation energy was checked again and was exactly the same as before, showing that the structure had not changed.

Vibrational Frequencies:

Number	Frequency	Infrared	D_3h Point group
1	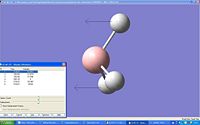1222.53	144.142	A₂
2	1300.38	26.1129	E'
3	1300.38	26.1129	E'
4	2637.65	0	A'₁
5	2757.65	146.21	E'
6	2757.65	146.21	E'

The Infrared Spectrum of BH₃

The spectrum only shows 3 peaks when there are 6 vibrations due to there being two pairs of vibrations (2 and 3, 5 and 6) which have the same frequency (degenerate) and one of the vibrations does not emit infrared (vibration 4).

Molecular Orbital Diagram of BH₃

Molecular Orbitals:

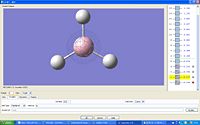
Orbital	Predicted MO	Calculated MO
1
2
3 (HOMO-1)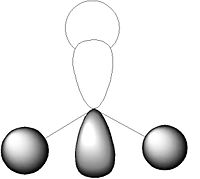
4 (HOMO)
5 (LUMO)
6 (LUMO+1)
7

The molecular orbitals predicted are very much like the computed. However the 3a'₁ orbital has not been included. This is because it looks like the 8th orbital in Gaussview and not the 6th. This could be due to mixing of the orbitals and thus increasing the energy of the antibonding s-orbital to higher than that of the degenerate pair which are at the moment in the MO diagram at the top. This would make the degenerate pair 6 and 7 (instead of 7 and 8). This is what is seen in the table above.

Excluding the effect of mixing the only difference seems to be that the computed MO is more diffuse and shows how the "real" orbitals mix togther - they fill more space than the drawn ones.

Cis and Trans Isomerism

The trans-Mo(CO)₂(PCH₃)₂ was optimised and the final energy came out as -773a.u. which is 2030449kJ/mol. This is a very high energy and certainly not one which we have been used to so far. The dipole is 0.0029D, this is low and would be expected as the two phosphine groups should cancel each other out. The point group came out to be C₁, but the real point group should be D_3h, this is beacause Gaussview likes the structures to be perfectly symmetric, which would be the case if the methyl groups were not on the phosphine. This calculation took 1hr 33min and 19s. The molecule can be seen at http://hdl.handle.net/10042/to-1215 .

The cis-Mo(CO)₄(PCH₃)₂ gave a final energy of 2030457kJ/mol. This is higher than the trans complex due to the steric strain from the 2 bulky phosphine groups being close to one another. The dipole is higher than trans at 8.8747D, it is generated from the 2 phosphine groups being close to one another and thereofore adding their charge together creating a dipole. The symmetry came out to be C₁, again this is wrong the actual symmetry is C_2h it is a lower symmetry than the trans. This calculation took longer than the trans at 1hr 52min 30s, this is because the programme has to deal with the steric strain, the complex is not as symmetrical as trans. The molecule was submitted to D-space at http://hdl.handle.net/10042/to-1216 .

The Mo-P bonds were shorter in the trans isomer (2.57Å v. 2.652 and 2.648Å) showing that having the 2 phosphine groups cis to one another increases strain and therefore the bond length. This is comparable to the litrature of 2.5Å for the trans and 2.576 and 2.577Å¹

The Mo-C bond had 2 different lengths in the cis isomer one which was on the same plane as the C₂ axis at 1.98Å and the others perpendicular to the z-axis at 2.03Å these are longer as the bulky phospine groups push out the CO ligands. This is also discribed in the litricture as the Mo-C bonds trans to a phosphine group is shorter than than a Mo-C bond cis to a phosphine group¹.

However the bond lengths are the other way round when it comes to the C=O lengths, the C=O in th same plane as the phosphine groups have a longer bond length than their counterparts - 1.192Å v 1.188Å. In the trans isomer the C=O lenth is 1.190Å which is in the middle of the 2 cis lengths. I would expect this as all the CO ligands are equivalent and therefore the steric strain would average.

The P-Mo-P angle in the cis isomer is 95.358 degrees. The litrature state this as 104.62, or anything over 90 degrees is expected. The lit is based upon a PPh₃ ligand whereas the ligand used here only has methyl substituents therefore the angle would be expected to be smaller than that cited!

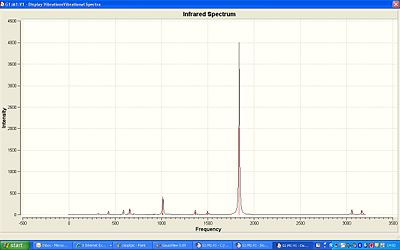
The IR for the trans isomer shows one strong band at 1839cm^-1 this is the C=O stretch. The lit^-1 value for this was 1891cm^-1 which is resonably close to the calculated. The spectra was publised in D-space at: http://hdl.handle.net/10042/to-1221

The cis isomer shows a broader band between 1849-1870cm^-1. This is also due to the C=O strech but there are 4 different stretching modes, 2 symmetric ones at 1849 and 1850 and then 2 asymmetric at 1870cm^-1 and 1960cm^-1. Compared with the lit² 4 bands are to be expected however they would normally occour at 2022, 1917, 1903 and 1882cm^-1.The spectra can be found at http://hdl.handle.net/10042/to-1222 .

The decrese in the stretching frequency is due to more electron density going into the π* orbital and therefore decreasing the CO bond. With the phosphines trans to each other more electron density is donated to the Mo and therefore onto the π* orbital of CO.

The trans geometry has decreased the stretching frequency of the C=O bond

Hogarth G, Norton T, Inorg. Chemica Acta, 254 (1997), 167-171.
A. D. Allen and P. F. Barrett, Can. J. Chem., 1968, 46, 1649.

NH₃ molecule

The initial structure of NH₃ was optimised and the symmetry was determined to be C_3v, the energy was -56.53188590a.u. All the bond lengths are the same at 1.00591Å and 2 of the angles are the same at 116.25108°, the other is 116.25113°. The calculation took 33s.

After one bond was lengthened to 1.01Å from 1Å the optimisation gave the new symmety of C₁, and the dipole was slightly increased by 0.0180Debye and the energy increased by 0.00000168a.u. There is not much of a change however the bond lengths are all slighty different with 2 being 1.00596Å and the other 1.00597Å. Each angle is also different (116.14373°, 116.13684° and 116.13694°). These slight differences could be dimished by more iterations. This calculation too slightly longer at 43s.

This optimisation had a very slightly lower energy than the others at -56.53154189 a.u. The symmetry was changed to D_3h. There is now no dipole moment in the molecule and the angles show an almost planar molecule with 2 being 120.00002° and the other 119.99997°. Also all the bonds are now the same length at 1.00037Å. The molecule has a lower energy as it is almost planar and highly symmetrical. This calculation took the longest at 1min 14s.

The symmetry has made a difference to the structures. The higher the symmetry the more planar and regular the bond lengths and angles. The time taken to optimise the geometries did not correlate with the symmetry as the highest symmetry group took the longest amount of time and the lowest symmetry to the middle amount of time to optimise. Therefore the symmetry does not have any effect on the time taken. However i believe it would make sense that the higher the symmetry the shorter the amount of time taken to optimise as a highly symmetrical molecule would be easier due to the molecule being the same all over.

A molecule can breaks symmetry when the wavefunction does not make an irreducible representation of the point group¹ this is basically where groups are assumed to be the same (equivalent) and therefore the energies are "averaged". When the symmetry breaks the output of the calculation can be suspect². However for high symmetry molecules this does not matter very much as they are very symmetric and therefore can be "averaged"³.

The lowest energy geometry is the planar molecule with a D_3h point group with 148423kJ/mol (using a conversion of 2625.4996). The difference between the C₁ group is 0.9076kJ/mol and with C_3h the energy difference is 0.9032kJ/mol. The energy difference is very slight when seen in kJ/mol thereofOre they are not significant.

The first optimisation using the MP2 method on the C_3v molecule took 38seconds and had an energy of 148178.3764kJ/mol. The calculation was quicker than the lower level previous calculations.

This optimisation of the D_3h gave an energy of 148148.1447kJ/mol. The calculation took 21s which is much shorter than the its previous version.

The difference in the energies is 30.32kJ/mol compared with the experimental value of 24.3kJ/mol the computation was very close! The difference between the 2 differet kinds of calculations and the energies has changed by around 300kJ/mol, this is quite a significant change!

Vibrational Frequencies:

C_3v:Number	Frequency	Infrared	D_3h: Number	Frequency	Infrared
1	1056.18	182.455	1	89.494	837.82
2	1730.94	14.5841	2	1658.37	53.4338
3	1730.94	14.5841	3	1658.37	53.4315
4	3551.89	14.584	4	3523.58	0
5	3688	3.4787	5	3736.63	18.2536
6	3688	3.4787	6	3736.63	18.2547

Comparing vibrations between different point groups:

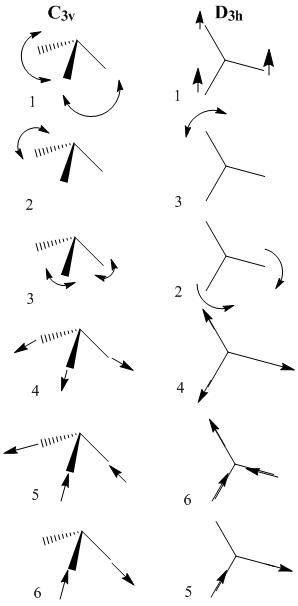
The vibrations are much the same for the different point groups. Only the degenerate vibrations are swaped around.

Compared with the lit⁴ values of 3534, 3464, 34634, 1765, 1765,and 1139cm^-1 the computed frequencies are far out for some of the vibrations, for instance the 2 degenerate orbitals 5 and 6 are actually 4 and 5 in the lit values, and they are out by 200cm^-1. The other degenerate vibrations are only out by 30cm^-1, this was a good approximation for them, and also for vibration 4(on guassview)/6(from lit) 3534cm^-1 and 3551cm^-1 are only out by 17 wavenumbers! the first vibration however is about 100 wavenumbers out. The computer can generate a resonable prediction of the IR spectrum but not accurate numbers.

For the transition state the negative frequency is at 3523.58cm^-1.

The vibration that follows the reaction path is number 1 in each point group - these correspond to a frequency for C_3v at 1056.18cm^-1 and D_3h at 89.49cm^-1.

Sherril C, Lee M, Head-Gordon M, Chemical Physics Letters 302 (1999), 425-430 DOI:10.1016/S0009-2614(99)00206-7
Davidson E. and Borden W. J. Phys. Chem, 1983, 87 (24), 4783-4790 DOI:10.1021/j150642a005
S. Prestwich, B. Hnich, R. Rossi, S. A. Tarim, Symmetry Breaking by Nonstationary Optimisation http://4c.ucc.ie/~rrossi/symcon08slides.pdf
http://www.chem.purdue.edu/gchelp/vibs/nh3.html

Mini Project

Hydrogen is a very desirable tool with use in fuel cells. It only needs to be reacted with oxygen in order to produce energy. It is a very clean reaction with the only product being water. Therefore a lot of research has been done on the use of producing hydrogen to be used as a fuel.

Ammonium borane is used as a way of storing hydrogen. It has a high content of hydrogen in it and is quite stable as a solid at room temp. It has a strong N-B bond making hydrogen evolution more desirable over N-B bond breakning. The by-product of hydrogen evolution is borazine – isoelectronic to benzene. The eclipsed and staggered conformations were optimised, first using B3LYP with a basis set of 3-21G, and then a higher set of MP2 and 6-311G(d,p) to increase the accuracy. The difference between the accuracy was around 0.2au –this correlates to 525kJ/mol, which is quite a difference!

The optimisation of the staggered conformation came to 217810.8471kJ/mol and the eclipsed was slightly higher at 217826.9733kJ/mol.

There is a difference of 16.1kJ/mol.

It is expected that the staggered is lower due to the reduction of the hydrogen’s repelling each other.

Using the equation ΔE=E_reactants-E_products, it is possible to calculate the change in energy of the NaNH₄ and BH₄Cl reaction:

NaNH₄ + BH₄Cl -> H₂NBH₃+ NaCl +H₂

The optimisation energies of each molecule was calculated as follows, for NaNH₄ and BH₄Cl the iosns were calculated separately. This however is not very accurate as the energy calculated is in the gas phase whereas the actual reaction is carried out in the solid phase.

Na⁺=424291.8486

BH₄⁺ =71218.15291

NH₄⁺ = 149429.6007

Cl^- = 120694.859

NaCl = 1631946.662

H₂=3046.294433

NH₃BH₃ = 217810.847 kJ/mol

ΔE=E_reactants-E_products

=765634.4612-1852803.803

=-1087169.342kJ/mol

=-1087000kJ/mol

This energy release is very high showing it is an easy reaction in order to make NH₃BH₃

Comparison with ethane

The staggered conformation ethane has an energy of 208913.3361kJ/mol. This is lower than that of NH₃BH₃, this is because the molecule is more symmetrical. The eclipsed ethane has a lower energy than the staggered at 208899.9541kJ/mol. This is only a difference of 13.4kJ/mol. There is more of a difference between the ammonium borane due to the nitrogen and borane having different sized nuclei.

Molecular orbitals of ethane and ammonium borane

Comparing the HOMO and LUMO of each molecule allows us to see the potential reactivity of them.

This is the HOMO of ammonium borane. It is an anti-bonding orbital with most of the electron density on the more electronegative nitrogen.

This is the HOMO of ethane. It is also an antibonding orbital – but unlike ammonium borane the electron density is evenly distributed as it is homoatomic. Therefore this will be a lower energy than ammonium borane. This is true for all the MOs of ethane – the charge is evenly spread therefore ethane is less likely to get rid of hydrogen, unlike ammonium borane – where the electron density is not evenly distributed and therefore it likes to evolve hydrogen in order to make borazine.

Ethane optimised structure and MOs: http://hdl.handle.net/10042/to-1320 Ammonium borane optimised structure and MOs:http://hdl.handle.net/10042/to-1321

Borazine

Ammonium borane evolves H₂ in order to make its more stable borazine – which is isoelectronic to benzene the energy of borazine is 635355kJ/mol.

The overall energy is as follows: 3NH₃BH_£ → N₃B₃H₆ + 6H₂ Therefore using the equation of products-reactants the overall energy change is: (6(3046)+635355)-(3(217810)=201kJ/mol. This is a favoured reaction and is why ammonium borane is so good at evolving hydrogen and therefore a good source of it for fuel. D-space borazine - http://hdl.handle.net/10042/to-1319

Borane leads the way to alternative fuels http://www.rsc.org/Publishing/ChemScience/Volume/2008/08/Borane_fuels.asp
Frances H. Stephens, Vincent Pons and R. Tom Baker, Royal Soc. Chem., 2007, 2613–2626DOI:10.1039/b703053c

BCl3 Molecule

Small Molecule(H2O)

BH3 Molecule