Rep:Mod:taa063

Module 3: Experiment 3: The Transition States

Introduction

In the first part of this experiment the Cope rearrangement of 1, 5-hexadiene will be studied using computational methods. It is thought that the mechanism proceeds via a chair or boat transition state. The low-energy minima and transition structures of the 1, 5 – hexadiene will be calculated and used to determine the reaction mechanism.In the next part of the experiment the Diels Alder reaction will be studied.

Optimizing the Reactants and Products:

Anti-Conformer

A molecule of 1-5 hexadiene was drawn in which the central four carbons were organized in an anti-periplanar arrangement, that being the dihedral angle of the central four carbons was modified to 180 degrees This molecule was then optimized using the HF/3-21G method and the point group was determined by the Gaussian symmetrize function.

Gauche Conformer

1, 5 -hexadiene was also drawn so that the central four carbons were organized in a gauche arrangement , that being the dihedral angle of the central four carbons was modified to 60 degrees.The molecule was also optimized using the HF/3-21G method and the point group was determined. It is expected that the gauche structure will be higher in energy due to the fact that there is more steric repulsion between alkyl groups in this conformation.The results can be seen below:

Anti Calculation Summary	Anti Optimized Structure	Gauche Calculation Summary	Gauche Optimized Structure

As you can see above the point group of the optimized anti structure is C_i and the energy of the structure is -231.69254 hartrees.Comparison to the appendix suggests that this is the lowest energy conformation as, the data corresponds to that of the anti-2 conformer .As for the optimized gauche structure, the point group is C1 and the energy of the structure is -231.6266 hartrees and corresponds to the gauche 3 conformer in the appendix. These results are not what is expected as the gauche structure is lower in energy by 0.000126 hartrees. One can only stipulate that this is can be attributed to the fact that this basis set does not provide the accuracy required to differentiate effectively between the conformers and thus these conformers were then further optimized by the B3LYP/6-31G(d) method to yield the following results:

B3LYP Anti Calculation Summary	B3LYP Gauche Calculation Summary

As you can see from above, the anti conformer as expected is now the more stable molecule. This hightlights the need for the use of a more accurate basis set and method when optimizing similar molecules. In order to see how the overall geometry of the molecule changes when the B3LYP/6-31G(d) is used opposed to the HF/3-21G method, the bond angles and bond lengths of the 1, 5-hexadiene were compared:

Method	HF /3-21G	B3LYP/6-31G(d)
Anti-Structure
Bond length (C 1-C2)/Angstroms	1.32	1.33
Bond length (C 2-C3)/Angstroms	1.51	1.50
Bond length(C 3-C4)/Angstroms	1.55	1.55
Bond length(C 4-C5)/Angstroms	1.51	1.50
Bond length(C 5-C6)/Angstroms	1.32	1.33
Dihedral Angle 1( C1-C2-C3-C4)	114.66	118.48
Dihedral Angle 2(C2-C3-C4-C5)	180.00	180.00
Dihedral Angle 3( C3-C4-C5-C6)	114.66	118.48
Energy/Hartrees	-231.69254	-234.61170

As seen above there are noticeable differences between the two optimized structures. The bond lengths differ by up to 0.01 angstroms but perhaps the most notable difference is that of the dihedral angles 1 and 3 which are some 3.82 degrees larger in the B3LYP/6-31G(d) optimized structure. These difference highlight again the need for the use of a more accurate basis set and method when optimizing molecules. As the final energy of the molecule outputted is only the bare potential energy surface, a frequency calculation needs to be carried out in order to compare the results with experimental values. The result of the frequency calculation of the anti-2 conformer can be seen below in the form of an IR spectrum:

As you can see from above there are no imaginary frequencies and further analaysis of the vibrations confirms this as there are 42 positive vibrational frequencies.

This calculation also outputted the following thermochemical energies:

Sum of electronic and zero-point Energies=           -234.469219
Sum of electronic and thermal Energies=              -234.461867
Sum of electronic and thermal Enthalpies=            -234.460922
Sum of electronic and thermal Free Energies=         -234.500817

Optimizing the "Chair" and "Boat" Transition Structures :

The transition states for the Cope rearrangement can either have a boat or chair conformation which consists of two ally fragments that are 2.2 Å apart.

Berny Transition State Optimisation of Chair Conformer

An allyl fragment was drawn and then optimized using the HF/3-21G method. A copy of this optimized molecule was then made and both fragments were then positioned so that the terminal ends were 2.2 Å apart and orientated such that they looked like the chair transition state seen in the appendix. This transition state was then optimized(Opt+Freq) to a TS(Berny) and the results can be seen below:

Berny Transition State Calculation Summary	Bermy Transition State Structure	IR spectrum

1) Length of bond forming 1/Angstroms	2) Length of bond forming /Angstroms	Imaginary vibration / cm-1
2.02	2.02	-817.977

As you can see from above in the IR spectrum there is an imaginary vibration at -817.977 cm^-1 which can be seen below.This vibrations corresponds to the Cope rearrangement.

Imaginary Vibrations

Optimization of Chair Conformer using the frozen coordinate method

The same input guess chair structure was now optimized by the frozen coordinate method. Initially the redundant coordinate editor was used to freeze the bond distances (2.2 Å) and the structure was then optimized to a minimum using the HF/3-21G method. Next, using this optimized structure, the redundant coordinate editor was used again but the coordinate parameters were changed to ‘bond/derivative’ . The transition state was now optimized as above except the force constants were not calculated.This yielded the following results:

Frozen Coordinate Method Calculation Summary	Frozen Coordinate Method Structure	IR spectrum

1) Length of bond forming /Angstroms	2)Length of bond forming/Angstroms	Imaginary vibration / cm-1
2.02	2.02	-817.936

Comparison between the two methods show how they both output very similar results and thus both methods are reasonable. However it must be noted that the first method(Berny Transition Optimization) is only effective if the guess structure for the transition structure is relatively close to the exact structure.

QST2 method

The QST2 method, which optimisizes to a QTS2 transition state, was used in order to optimize the boat transition structure as it interpolates between the below specified reactant and product structures whose dihedral angles were modified to 0 degrees and 100 degrees respectively so it resembled the boat transition structure:

Specified Reactant and Product

This yielded the following results:

QST2 Calculation Summary	QST2 State Structure	IR spectrum

1) Length of bond forming 1/Angstroms	2) Length of bond forming /Angstroms	Imaginary vibration / cm-1
2.14	2.14	-840.126

As you can see above there is one imaginary vibration at -840.126 and cm^-1 which again corresponds to the Cope rearrangement.

Intrinisic Reaction Coordinate method

The IRC method was used to study the reaction path of the optimized chair transition structure. The calculation was only run in the forward directions, the force constant= once and the number of points was set to 50. It was found that after 50 points the geometry was still not at a minimum therefore the following action was taken (i) Minimization of the transition structure after the 50 points (ii) The IRC was run again except the number of points was increased to 150 (iii) The IRC was run again with 50 steps except the Force Constant= always. Below are the results:

Graph(i): IRC for 50 points, force=once	Graph(ii):IRC for 150 points, force =once	Graph(iii):IRC for 50 points, force=always

As you can see above in graph i), the transition state has not reached a minimum geometry however in graph ii) and iii it appears the structure has been fully optimized as indicated by the RMS gradient which is close to zero.

Comparison of Theories

The chair and boat transition states were both optimized used using the B3LYP/6-31G(d) method. The geometries and energies of the optimized molecule was then compared to that of the molecule optimized using the HF/3-2G method. The results can be seen below:

Method	HF/3-21G Optimization of Chair TS	B3LYP/6-31G(d)Optimization of Chair TS	HF/3-21G Optimization of Boat TS	B3LYP/6-31G(d)Optimization of Boat TS
Bond length of bond forming/Angstroms	2.02	1.97	2.14	2.21
Angles(C1-C2-C3/C4-C5-C6)	120.49°	119.96°	121.86°,	122.27°
Energy/Hartrees	-231.61932	-234.55698	-231.60280	-234.54309
Imaginary Vibration (cm-1)	-817.997	-565.533	-840.126	-530.641

The table shows how there is very little difference in the geometry between the two levels however the energies differ quite significantly as well as the imaginary vibrations. The lower level theory is thus useful in getting a quick idea of the structure of the molecule.

Activation Energies

In order to calculate the activation energies of the transition states one needs to calculate the thermochemical energies of the transitions states as seen below. The activation energy of the transition states at 0K was calculated using the sum of electronic and zero point energies of the transition structures ( boat and chair) and the anti-2 reactant(c.f.-234.469219 at 0K):

Thermochemistry Data at 0K:

	Chair TS (B3LYP/6-31G(d))	Boat TS (B3LYP/6-31G(d))
Sum of electronic and zero-point Energies	-234.414929	-234.402342
Sum of electronic and thermal Energies	-234.409008	-234.396008
Sum of electronic and thermal Enthalpies	-234.408063	-234.395063
Sum of electronic and thermal Free Energies	-234.443815	-234.431097

From these values the activation energies of the two transition structures were calculated:

	Chair Activation Energies/kcal mol-1 at 0K	Boat Activation Energies/kcal mol-1 at 0K
Computed	34.0674	41.966
Experimental	33.5 ±0.5	44.7±2.0

As you can see from above, the easily, computed activations energies are a very good estimate of the experimental results.

Diels Alder Cycloaddition:

Optimization of Products and Reactants

In this part of the experiment the Diels Alder reaction between cis-butadiene and ethene will be studied. In order to determine the symmetry of the reactants and products they were first optimized using the semi-empirical AM1 method and then the orbitals were visualized to yield the following:

HOMO of cis-butadiene	Symmetry and Qualatative MO of HOMO	LUMO of cis-butadiene	Symmetry and Qualitative MO of LUMO
	HOMO is antisymmetric with respect to the plane		LUMO is symmetric with respect to the plane

HOMO of ethene	Symmetry and Qualitative MO of HOMO	LUMO of ethene	Symmetry and Qualitative MO of LUMO
	HOMO is symmetric with respect to the plane		LUMO is antisymmetric with respect to the plane

As you can see above, there is a good match between the calculated molecular orbitals and the qualitative molecular orbtials. You can also see from the symmetries of the orbtials that the HOMO-LUMO overlap of butadiene and ethene which is necessary for the reaction between reactants is possible.

Transition State

The transition state was drawn, by firstly optimizing using the HF/3-21G method a cyclohexene with a -CH2-CH2- fragment group bridged from the cyclohexne carbons 2 to 5. This was subsequently removed and the distance between terminal carbons was then set to 2.2 Å.This guess transition state was then optimized(Opt+Freq) to TS Berny by the HF/3-21G method and the resultant structure can be seen below:

Transition State Structure

The molecular orbitals were also visualized as seen below:

HOMO of transition state	Symmetry of HOMO	LUMO of transition state	Symmetry of LUMO
	HOMO is symmetric with respect to the plane		LUMO is symmetric with respect to the plane

The results of the calculated MOs show how both HOMO and LUMO transition states are symmetric about the plane. This is what we would expect as the transition state should resemble the overlap of the reactant HOMO-LUMO orbitals. As you can see above, both combinations of the reactant HOMO-LUMO orbital result in a symmetric product as the the overlap of the anitsymmetric ethene LUMO with the antisymmetric butadiene HOMO results in a symmetric structure as well as the overlap of the symmetric ethene HOMO with the symmetric butadiene.The geometry of the optimized transition state structure was then analyzed and compared to literature values.

Method	HF /3-21G
Transition State Structure
Bond length (C1 -C2/C3-C4)/Angstroms	1.37
Bond length (C4-C5/C1-C6)/Angstroms	2.21
Bond length(C5-C6)/Angstroms	1.38
Bond length(C2-C3)/Angstroms	1.39
Energy/Hartrees	-231.6032

From above you can see the results are what one would expect as the length of the sp³ carbons in the optimized transition structure are slightly larger than the typical sp³ bond length(1.54) implying that the bonds are not completely formed yet. In saying that we know that there is some interaction of orbitals present as the bond length is shorter than twice the value of twice the van der waals radius( ~3.4 angstroms). Furthemore the expected sp² carbons have a longer bond length than expected again highlighting the fact that in the transition state the bond have not properely been formed yet.

The frequency was also calculated and there was again one imaginary vibration at -818.366 cm^-1. The negative vibration was visualized as seen below:

Imaginary Vibration

The negative vibrations show that for the two single bonds that form a bond, the length between the two atoms forming a bond is decreasing. It also shows how these bonds are being formed at the same time.

Regioselectivity of the Diels Alder Reaction

For this part of the experiment, the diels alder reaction of 1,3-hexadiene and maleic anhydride will be investigated. The product of this reaction can either have an endo or exo form, with the endo form being the preferred product. In order to confirm this the two possible products were drawn and then optimized using the AM1 semi-empirical method. They were then disconnected to form the reactant structures and optimized(Opt+Freq) to Berny as before which resulted in the following results:

	Endo Transition State	Exo Transition State
Structure
Bond length of bond forming/Angstroms	2.16237	2.17040
Energy/Hartrees	-0.05159427	-0.05050317
Imaginary Vibration (cm-1)	-805.656	-811.376

As you can see above the exo transition state is higher in energy by 0.685 kcal/mol and to provide a reasoning for this the molecular orbitals for the two structures was visualized:

HOMO of Endo Transition State	LUMO of Endo Transition State

HOMO of Exo Transition State	LUMO of Exo Transition State

The reasoning for the stability of the endo product is said to be due to secondary orbital overlap between the HOMO of the dienophile cyclopentaidene and the LUMO of the diene such as that witnessed in the diagram below:

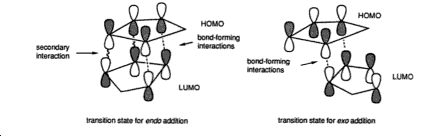
However by looking at the HOMO and LUMO molecular orbitals of the endo product it appears that the only electron density between the diene and the dienophile is the primary overlaps, that being sigma bond.Furthermore when comparing the endo and exo frontier orbitals it must be noted that they look remarkable similar and that the endo form when compared does not have any extra electron density in the frontier orbitals that would results in secondary overlap.Thus this computated molecular orbital’s have refuted this hypothesis however in saying this if one was to compute more molecular orbital’s that being HOMO-1 or the LUMO+1 one might be able to find an orbital overlap which does in fact stablise the structure.