Rep:Mod:taa062

Module 2: Bonding(Ab initio and density functional molecular orbital)

Introduction

In this lab we will use computational methods such as DFT and MP2 in order to analyse structure and bonding in inorganic complexes. As seen in this lab, these methods allow us to calculate the energy and location of transition states. Furthermore these computational methods can be used to generate IR and NMR spectrums and other useful information about complexes and molecules such as their dipole moments.

BCl₃

Using the B3LYp method and the basis set LANL2MB, the optimised structure of BCl₃ was calculated which yielded the following results:

Results Summary	Optimization Graphs

Optimised B-Cl bond distanc(A o)	Optimised Cl-B-Cl bond angle (o)
1.87	120.0

Discussion:

As you can see from above the computer generated results which we would expect for BCl₃.It describes the point group of the molecule to be D_3h which we know is the case from group theory.It also describes the fact that the molecule has no net dipole which is obvious due to the fact that the molecule is highly symmetrical, thus individual dipoles cancel each other out. The optimization time was extremely fast as it took only 11 seconds and as seen in the above graph it occurred in 2 optimization steps.

NH₃

Using the B3LYp method and now the basis set 3-21G , the optimised structure of NH₃ was calculated which yielded the following results:

Results Summary	Optimization Graphs

DOI:10042/to-1980

Optimised B-Cl bond distanc(A o)	Optimised Cl-B-Cl bond angle (o)
1.22	110.2

---

Center     Atomic     Atomic              Coordinates (Angstroms)
Number     Number      Type              X           Y           Z
---------------------------------------------------------------------
   1          7             0        0.000000    0.000000    0.098313
   2          1             0        0.000000    0.968498   -0.229397
   3          1             0       -0.838744   -0.484249   -0.229397
   4          1             0        0.838744   -0.484249   -0.229397
---------------------------------------------------------------------

Discussion As you can see from above the computer generated results which we would expect again for NH₃.It describes the point group of the molecule to be C_3v which we know is the case from group theory.It also describes the fact that the molecule has a net dipole(1.8681) which is to be expected as the molecule is not highly symmetrical and thus individual dipoles are not cancelled.The optimization time was extremely fast as it took only 19 seconds and as seen in the above graph it occurred in 3 optimization steps.

BH₃

Vibration Frequencies

The vibrational frequencies of BH₃ were calculated and then animated in Gaussian. The results can be seen in the table below and also the symmetry that was assinged for each vibration:

No.	Form of the Vibration	Frequency/ cm-1	Intensity	Symmetry D3h point symmetry
1		1145.71	92.70	A2
2		1204.66	12.37	E'
3		1204.66	12.38	E'
4		2592.79	0	A1'
5		2731.31	103.83	E'
6		2731.31	103.83	E'

IR spectrum

The IR spectrum was then outputted in Gaussian as seen below. As one can see there are only 3 peaks in the spectrum whereas as shown above there are clearly six vibrational frequencies. This can be attributed to the fact that vibration number 4 has an intensity of 0 and thus will not appear on the spectrum. Also it can be seen above that vibrations 2 + 3 have the same frequency and thus will only appear as one single peak in the IR spectrum. This is also the case for vibrations 5 + 6.

Molecular Orbitals

Gaussian was used in order to obtain molecular orbitals of the BH₃ optimised molecule. These computed MOs were then compared to the MOs in the MO diagram for BH₃as seen below.As you can see from the table there is a good correlation between the qualitative MOs and the computed MOs however as seen below there are significant differences between them. For the qualitative MOs, the atomic orbitals appear separately whereas for the quantitative MOs, adjacent atomic orbitals which have the same phase overlap and appear as single lobe. Another noticeable difference is that in the quantative MOs, adjacent orbitals which are out of phase appear separately however unlike the qualitative MOs, they are clearly divided by nodes.These results indicate that qualitative MO theory is an effective and useful way of predicting accurately MOs as they can be easily generated without the need for time consuming calculations and computer modelling software.

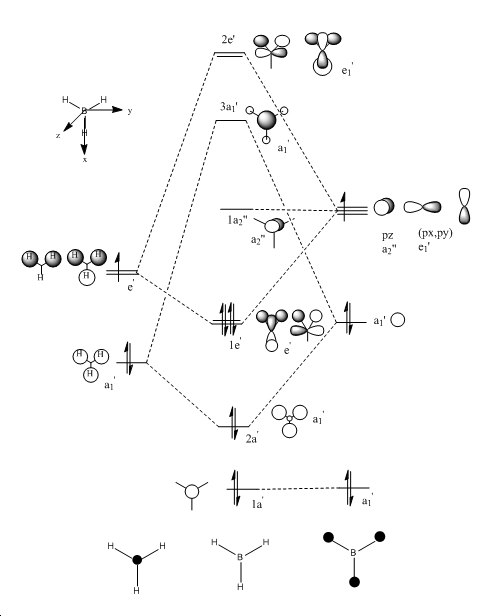
No.	Computed MO diagram	Qualitative MO diagram	Energy
1			-6.730
2			-0.517
3			-0.356
4			-0.356
5			-0.074
6			0.188
7			0.188
8			0.191

Cis and Trans isomerisation of Mo(CO)₄(PPh₃)₂

The complex Mo(CO)₄(PPh₃)₂ can exist in two forms that being the trans isomer and the cis isomer. Using two different optimization methods these isomers were optimized and then the vibrational spectrums of the two isomers were calculated. The cis and trans isomers were firstly optimized using the B3LYP/LANL2MB method and then further optimized using the B3LYP/ LANL2DZ. The optimized bond lengths and angles can be seen in the table below along with the literature values for the trans isomer and the cis isomer

Isomer	Mo-P bond length/Å	lit Mo-P bond length/Å	Mo-C bond length(cis to PMe3) / Å	lit Mo-C bond length(cis to PMe3) / Å	Mo-C bond length(trans to PMe3 / Å	lit Mo-C bond length(trans to PMe3)/ Å	Angle (P-Mo-P)o	lit Angle(P-Mo-P)o
cis-Mo(CO)4(PMe3)2 DOI:10042/to-1981	2.651/2.647	2.522	1.981, 1982	1.966, 1.975	2.032	2.042, 2.022	95.33	97.54
trans-Mo(CO)4(PMe3)2 DOI:10042/to-1982	2.572	2.500	N/A	N/A	2.028	2.005, 2.0161	179.992	180.000

As you can see from above the isomer which has the best correlation between the calculated and literature values is the trans isomer despite being compared to a slightly different complex (Mo(CO)₄(PPh₃)>)₂)).For the trans isomer, the calculated Mo-P bond deviates from the literature value by only 2.88% and the maximum deviation of the calculated Mo-C bond from literature is again only 1.15%. The best correlation though is the P-Mo-P angle which is within 0.55% of the literature values. As for the cis isomer the calculated Mo-P bond deviates from the literature by 5.11% yet the maximum deviations of the Mo-C from the literature is 0.76%. The P-Mo-P deviates by only 2.26%. In light of these results one could suggest that this model is a very good approximation of the experimental values however it has its limitations.

In both the cis and trans isomers the Mo-C bond length correlates better than the Mo-P to the literature. This can be attributed to the fact that the LANL2DZ method does not account for the dAOs on phosphorus and therefore does not account for the back bonding of the metal d orbitals to the phosphorous atom, which results in the shortening of the Mo-P bond. Therefore, the calculated Mo-P bond length is longer than the literature value. Comparing the two isomers, it can be seen that the Mo-P is 0.079 Å longer than the trans isomer. This is to be expected as in the cis isomer, the phosphorus groups are close together and thus the longer the Mo-P bond length, the smaller the steric clash and destabilisation of the complex. Furthermore by comparing the isomers it can be seen that for the cis isomer there are two Mo-C bonds. The Mo-C bond which is trans to the P(Me₃) group is shorter than the Mo-C bond which is cis to the(PMe₃) by 0.67 Å. This can be attributed to the fact that C=O is a strong trans influencing ligand compared to the phosphine group. Therefore there is more back donation from the metal to the C=O group when the phosphine group is trans to it however when the C=O group is trans to it ( cis to (PMe₃) , they effectively cancel each other out as they are of equal strength and thus comparatively these Mo-C bonds are longer.

IR spectra

The vibrational spectrum of the two complexes was then calculated to yield the following results:

Cis Isomer	Trans Isomer

Isomer	v(CO)/ cm-1	Intensity	v(CO)/ cm-1	Intensity	v(CO)/ cm-1	Intensity	v(CO)/ cm-1	Intensity
cis-Mo(CO)4(PMe3)2DOI:10042/to-1984	1848.41	1068.79	1850.68	1960.95	1869.91	666.097	1960.41	321.71
trans-Mo(CO)4(PMe3)2 DOI:10042/to-1983	1839.14	2000.08	1839.33	2008.03	1882.75	0.0005	1954.59	0.0001
lit cis-Mo(CO)4(PMe3)2	2012.4	-	1913.7	-	1898.5	-	1866.7	-
lit trans-Mo(CO)4(PMe3)2	1866.1	-	1885.4	-	1933.9	-	2050.4	-

In the IR spectrum for the cis isomer there are 4 peaks which is expected because as seen above, there are four vibrational frequencies with relatively high intensities. Although there are also four vibrational frequencies for the trans isomer, only one peak is observed in the IR spectrum. This can be attributed to the fact that two of the vibrational frequencies have intensities of zero and the other two frequencies have very similar absorptions and thus appear as one peak. This pattern also appears in the literature spectrums and thus this method and basis set provide an effective way of distinguishing between the two isomers. However this method is limited as the computer vibrational frequencies are significantly lower than the literature values.

Relative Energies of the cis and trans isomers

	Cis Isomer	Trans isomer
Energy/kJ mol-1	-2030456	-2030449

As seen above these results conflict with the literature as the literature states that the trans isomer is more stable as in this configuration steric repulsion is minimized. However the computed energy values show how the cis isomer is more stable by 7 kJ/mol. The method therefore can not accurately predict the most stable isomer and perhaps in order to improve it, the d orbtials of phosphorus need to be considered in the calculations.

We can alter the stability of the cis and trans isomers by changing the ligands, for example having an electron donating ligand instead of an electron withdrawing ligand. The stability can also be changed by adding a bulkier ligand for example.

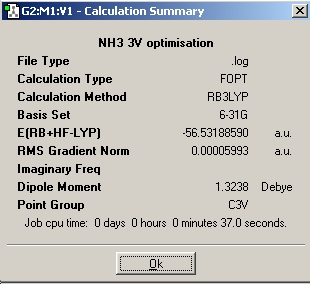
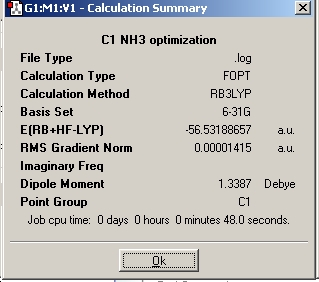
Ammonia

In the part of the experiment one will look at different isomers of NH₃ in order to analyse the effect of symmetry on structures, energies and optimisation time. Using the, 6-31G basis set and the B3LYP method the following isomers of NH₃ were optimized.

C3v	C1	D3h

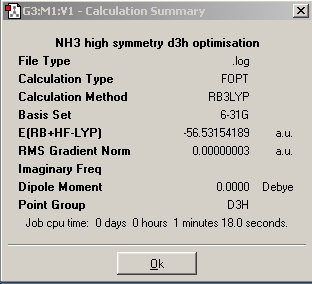As seen above, the higher the symmetry the quicker the molecule is optimized as the C₁ isomer takes 48 seconds to optimize whereas the high symmetry D_3h isomer takes 18 seconds to optimize. The high symmetry D_3h took the shortest time as the more symmetrical a molecule is, the fewer the possible arrangements of the molecule (fewer optimisation steps). This general trend is seen because the isomers in this experiment retained their geometry during the optimisation. The molecule with the lowest energy is the C₁ isomer and the molecule with the highest energy is the D_3h isomer and the energy difference between the two is 0.908 kJ/mol. The energy difference between D_3h and C_3v is calculated as 0.903 kJ/mol This suggest that the inversion between isomers can occur relatively easily and at room temperature ( RT=2.48 kJ/mol)

Effect of using different methods

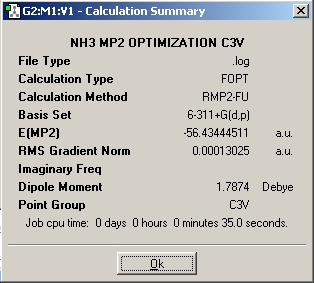
In order to determine how changing the basis set affects the results, the same C₁ and D_3h isomer were optimized however instead of using the B3LYP/ 6-31G method, the MP2/6-311+(d, p) method was used. The results are shown below:

C3v	D3h

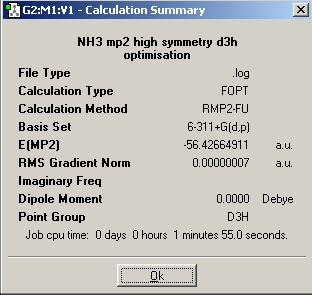As seen above the MP2 method has longer optimization times compared to the B3LYP/ 6-31G method however the former is significantly more accurate. The energy difference between the two isomers is 20.47 kJ/mol which is a good estimate of the literature value which is 24.3 kJ/mol .This can be compared to the 0.9 kJ/mol energy difference that was calculated using the B3YLP method.According to the results of the MP2 method, the conversion between isomers would not occur at room temperature as the energy required for this transition is far greater than the thermal energy at room temperature. However as suggested in the literature this can be attributed to the fact that the cause of this inversion is now thought to be quantum tunnelling and and as a result inversion can occur as the particles go through a potential barrier higher than the kinetic energy of the particle.

Inversion Mechanism

A scan was taken, in order to show the reaction pathway between the C_3v isomer and the D_3h and the results can be seen below:

Vibration

The vibrational spectrum was then calculated, the results are tabulated below:

No.	Form of the Vibration of C3V isomer	Frequency/ cm-1	Form of the Vibration of D3h isomer	Frequency/ cm-1
1		452.30		-318.05
2		1680.47		1640.59
3		1680.47		1640.59
4		3575.43		3635.71
5		3775.76		3854.27
6		3775.76		3854.27

Number	Experimental frequency for C3V isomer/cm-1	Calculated frequency for C3V isomer cm-1
1	950	452
2	1627	1680
3	3337	3576
4	3444	3776

IR spectrum for C3V isomer

As seen above the vibrations are very similar to that observed for the BH₃ molecule. However as seen above there is a key difference in that one of the frequencies for D _3h vibrations is negative(-318.05). From this we can conclude that this structure is the transition state. The vibration that follows the reaction pathway is the 452.30 vibration of the C _3v isomer and the (-318.05) vibration of the D _3h structure.

Although the IR spectrums shows the same number peaks as the literature IR spectrum, one can see that the calculated frequencies deviate significantly from the results.

Mini Project: Fuels of the future

Recently a significant amount of research has gone into the use of ammonia borane (NH₃BH₃ ) as a hydrogen fuel source due to the fact that this compound has a high content of realisable hydrogen and is solid at room temperature and thus allows for easy storage. In this experiment the structure of ammonia borane was analyzed and compared to the organic analogue ethane.

Ammonia borane can either adopt a staggered or eclipsed conformation and in order to determine which conformation is more stable the two conformations were optimized as seen below. In light of the results of the other parts of this project the decision was made to use, the most accurate method encountered thus far, that being the MP2//6-311+g(d,p)method. The results can be seen below:

Eclipsed Structure of AB DOI:10042/to-1937	Optimization Summary	Staggered Structure of AB DOI:10042/to-1938	Optimization Summary

From above you can see that he staggered conformation is the most stable conformation and this by 10.34kJ/mol.In order to provide a reasoning for this the bond distances in the structures was measured:

	Average H-H bond distances/A	B-N bond distances/A
Staggered Conformation	2.57	1.65
Eclipsed Conformation	2.37	1.68

As you can see from above the B-N bond distance is shorter in the staggered conformation, suggesting that the B-N bond is stronger and that the overlap of orbitals is better in this conformation.Furthermore, the H-H bond distances are longer in the staggered conformation compared to the eclipsed conformation and this stablizes the molecule as there would be less steric repulsion betweeen the hydrogen groups.

The same calculations were carried out on the organic analogue ethane for comparison:

Eclipsed Structure of Ethane	Optimization Summary	Staggered Structure of Ethane	Optimization Summary

As you can see above ethane is more stable than the ammonia borane. In order to get an idea of the reasoning for this, the MO's of the staggered conformers are both species were investigated. The results can be seen below:

HOMO for ethane	HOMO for ammonia - borane

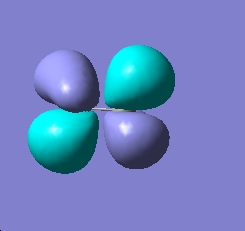From the MOs seen above it is fair for one to suggest that the stability of the ethane molecule compared to the ammonia borane molecule is due to the fact that there is a better overlap between orbitals, hence stablizing the structure.The better overlap is a results of the fact that the orbitals sizes are relatively close however in ammonia borane, there is a bigger mismatch in sizes. The bonding in ammonia borane is said to be dative as a results of the lone pair donation from nitrogen to the boron which is said to be a lewis acid. This can be seen in the MO's for ammonia borane as arguably the lone pair is donated into the large (B-H) antibonding orbtials seen on borane.Another noticeable difference between the results for ethane and ammonia borane is that the ammonia borane has a dipole moment whereas the ethane moelcule does not. This dipole which arises due to the differing electronegatives of boron and nitrogen, cause there to be a interaction between the boron hydrogens and the nitrogen hydrogens which greatly increases the melting point of the ammonia borane relative to the ethane.

Relative Stabilities of Reactants and Products

In order to calculate the stability of the products relative to the reactants, they were optimized using the same method and the results can be seen below:

Reactant NaBH4	Reactant NH4Cl	Total Energy/Hartrees
		-705. 57

Product NaCl	Product NH3BH3	Product H2	Total Energy/Hartrees
			-705.63

As you can see above the products are more stable than the reactants by 157.5 kJ/mol which is to be to be expected as the formation of ammonia borane also results in the production of H₂ gas which of course is entropically favourable.