Rep:Mod:taa061

Module 1: Structure and spectroscopy (Molecular mechanics and molecular orbital)

Introduction

In this experiment,Molecular Mechanics was used in order to predict the geometry and regioselectivity of a range of chemical reactions. In order to do this ChemBio3D using MM2 was used which calculates the energy minimum by optimizing molecular geometry.

This optimized total energy consists of contributions from stretching, bending, torsion, van der Waals and hydrogen bonding terms. Comparison of these terms in two different isomers provides reasoning for why one isomer is more stable. It must however be noted that Molecular Mechanics is limited in that it can not model ‘kinetic control’ of a reaction.

Dimerisation of Cyclopentadiene

Cyclopentadiene dimerises in a Diels Alder reaction to give preferentially the endo dimer(2) rather than the exo dimer( 1) as shown below:

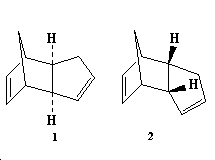
In order to compare the relativie stabilities of these two dimeris their geometries were optimized using the MM2 force field option in Chem 3D and these can be seen in the table below:

Energy component (kcal/mol)	Exo Dimer 1	Endo Dimer 2
Stretch	1.2923	1.2515
Bend	20.5870	20.8441
Stretch-bend	-0.8413	-0.8315
Torsion	7.6715	9.5062
Non-1,4 VDW	-1.4358	-1.5105
1,4 VDW	4.2320	4.3065
Dipole-dipole	0.3778	0.4455
TOTAL	31.8834	34.0117

From the above table it can be seen that the exo dimer(1) is thermodynamically more stable than the endo dimer ( 2) by an energy difference of 2.1283 kcal/mol. By analysis of the table above it can be seen that that the largest contribution of this energy difference can be attributed to the increase in the torsion energy term in the endo dimer by 1.8347 kcal/mol. This increase in torsion energy was rationalized by calculating the torsion/dihedral angles in the two isomers as seen below:

Endo Torsion Angle 1	Endo Torsion Angle 2	Exo Torsion Angle 1	Exo Torsion Angle 2
50.3o	46.7o	179o	177.5o.

As you see above the C-C bonds in the exo isomer are virtually antiperiplanar( c.f. 180^o) whereas in the endo isomer they are almost gauche ( c.f. 60^o ) . As the dihedral angle is more favourable in the exo isomer as there is less Pauli repulsion, this molecule has a lower energy associated with it and thus is more stable.

However as mentioned above cyclopentadiene dimerises to give preferentially the endo dimer(2) and thus this must be due to kinetic control. This can be attributed to the fact that in the transition state of the endo isomer is stable due to secondary overlap of the homo and lumo orbital’s which is not possible in the exo isomer as seen below:

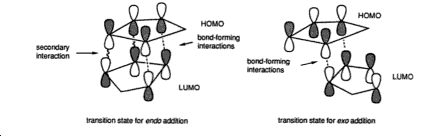
The Hydrogenation of Cyclopentadiene Dimer

Hydrogenation of the cyclopentadiene dimer can either occur on the double bond on the 5 membered ring (3) or 6 membered ring(4) as seen below:

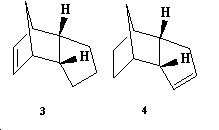
In order to determine which hydrogenation products are more stable, MM2 energies were calculated as seen below:

Energy component (kcal/mol)	Product 3	Product 4
Stretch	1.2324	1.1034
Bend	18.8651	14.5151
Stretch-bend	-0.7625	-0.5464
Torsion	12.2469	12.5123
Non-1,4 VDW	-1.5627	-1.0470
1,4 VDW	5.7523	4.4985
Dipole-dipole	0.1631	0.1408
TOTAL	35.9337	31.1767

From the above table you can see that product 4 is thermodynamically more stable than product 3. Furthermore from the table it can also be seen that this can largely be attributed to an increase in bend energy contribution in product 3 of 4.35 kcal/mol. Thus the deviations of the bond angles from their ideal value was analyzed in order to explain this increase in bend contribution in product 3:

Product	Bond angle: C=C-C	Bond angle: C=C-C
3	107.6o	107.4o
4	112.4o	112.7o

As you can see from above, the bond angles in product 3 deviate more from ideality than product 4 and thus this product is more stable. The C=C-C bond angle in product 3 deviates significantly from ideal sp²geometry( c.f 120^o ).Whereas in product 4 the C=C-C bond angle is closer to the ideal angle.Furthermore the deviations from ideality of the sp3 centres are larger in product 3.

These results are consistent with what one would expect to see as the formation of product 4 involves the release of ring strain in the 6 membered ring and would allow the bridged carbons to occupy angles closer to their preferred values. Arguably however under kinetic control, product 3 would form due to the steric hindrance of the bridged carbons.

Stereochemistry of Nucleophilic additions to a pyridinium ring ( NAD+ analogue)

The first reaction that was investigated was the reaction of the optically active derivative of prolinol with methyl magnesium iodide which alkylates position 4 of the pyridine ring with the absolute stereochemistry as shown below:

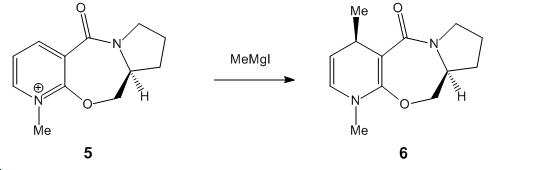
In order to explain this absolute stereochemistry, the prolinol derivative starting material was modeled using ChemBio3D and minimized using the MM2 force field. Below are the results for the lowest energy conformation:

Energy component (kcal/mol)	Prolinol Derivative 5
Stretch	0.8756
Bend	6.7310
Stretch-bend	0.1122
Torsion	9.5524
Non-1,4 VDW	-2.7159
1,4 VDW	11.4845
Charge/Dipole	3.2618
Dipole-dipole	-3.7834
TOTAL	25.5182

However, the total energy of the prolinol derivative starting material provides little information on why it has this absolute stereochemistry. An attempt was then made to model the prolinol derivative with the added MeMgI component however this resulted in an error, most probably due to the presence of the inorganic magnesium atom. Therefore, in order to understand the reason for this , and thus the reaction mechanism, the 3D model of the prolinol derivative was studied:

Compound5

As you can see above, the carbonyl group points up above the plane whereas the pyridine part of the molecule is relatively flat. This observation was confirmed in ChemBio 3D, where the dihedral angle of the carbonyl group was found to be 43^o . As mentioned previously product 6 has the above absolute stereochemistry, a result suggesting that the methyl group always adds to the prolinol derivative from top face. In light of these observations the below mechanism can be suggested which involves the coordination of the magnesium of the Grignard reagent to the carbonyl oxygen which causes the methyl to attack in the same face:

In the next example the pyridium ring of 7 is derivitised by a reaction with aniline to form 8 which in a reverse reaction transfers the NH Phenyl group to electrophiles as seen below:

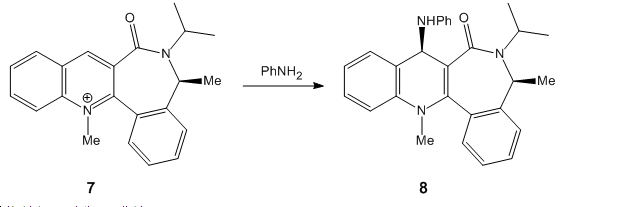
Below are the results for the lowest energy conformation of the starting material 7:

Energy component (kcal/mol)	Pyridium ring 7
Stretch	1.5354
Bend	6.6854
Stretch-bend	0.3343
Torsion	-6.0226
Non-1,4 VDW	-2.5932
1,4 VDW	17.6908
Charge/Dipole	2.3290
Dipole-dipole	-4.8189
TOTAL	15.1403

Again in order to get an idea of the reaction mechanism the 3D model shown below was analyzed:

Compound7

As seen above the carbonyl group points downwards which is confirmed by Chemi Bio3D which shows it to have a dihedral angle of -45.1 ^o .This is due to the fact that the , up facing bulky isopropyl substituent forces the adjacent methyl group downwards in order to avoid a steric clash which in effect forces the carbonyl group downwards. Unlike the Grignard reagent used in the previous example, the aniline does not contain a metal that can coordinate with the carbonyl oxygen and thus the aniline nucleophie additions is controlled by sterics and thus will add directly to the pyridinium ring of 7 on the opposite , less hindered face, in this case the top face.

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

As seen in structures 10 and 11, a key intermediate in the total synthesis of taxol can either have a carbonyl group pointing up or down.

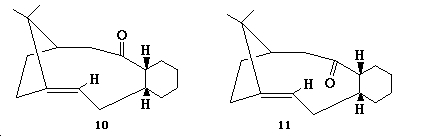
These two structures are atropisomers and in order to determine which structure is more stable, MM2 calculations were carried out on the intermediates to give the below results:

Energy component (kcal/mol)	Taxol Intermediate 10	Taxol Intermediate 11
Stretch	2.6788	2.5465
Bend	15.8374	10.6609
Stretch-bend	0.3947	0.3198
Torsion	18.2132	19.6969
Non-1,4 VDW	-1.0448	-1.3227
1,4 VDW	12.6481	12.5450
Dipole-dipole	0.1476	-0.1813
TOTAL	48.8749	44.2651

It was must be noted however that the above MM2 energies were obtained by manually forcing the six membered ring from a twist boat conformation into a chair conformation which significantly lowered the energy of the molecule.

As you can see above, intermediate 11, the atropisomer where the carbonyl groups points down has a lower energy. Analysis of the table shows how this can largely be attributed to the fact that intermediate 10 has a larger bend energy contribution that intermediate 11 by 5.17 kcal/mol. Thus again the deviations of the bond angles from their ideal value was analyzed in order to explain this increase in bend contribution in 10. Results are shown in the table below:

Intermediate	Bond angles around carbonyl	3D STRUCTURE
10	118.1o, 115.3 o	Taxolup
11	120.0o, 119.8 o	Taxoldown

As you can see from above, the bond angles in intermediate 10 deviate to a greater extent from the ideal sp² bond angles. As the deviations from ideality are greater in intermediate 10 it results in this isomer suffering from more bond strain thus accounting for why it is less stable than intermediate 11.

It has been noted that the alkene react slowly and this can be attributed to the fact that the alkene is this molecule is hyperstable , that being the alkene is more stable than the corresponding alkane. This can be attributed to the fact that upon functionalisation of the alkene, there is an increase in ring strain as molecule adopts its new geometry. As a result the transition state energy of the molecule is extremely high and thus the reaction proceeds at an extremely slow rate. This is typical for alkenes that are contained in a ring and results in a negative olefin strain energy.

How one might induce room temperature hydrolysis of a peptide

In this example, simple conformational analysis is used to rationalize kinetic behavior. In the below reaction, two isomers of a peptide-like molecule are hydrolyzed, one isomer reacts significantly faster than the other:

In order to establish the relative stabilities of the isomers and their conformers, MM2 calculations were carried out on the structures to yield the following results:

Energy component (kcal/mol)	13 ,amide axial	13, amide equatorial	14, amide axial	14, amide equatorial
Stretch	1.5771	1.6869	1.5224	1.5431
Bend	8.2688	5.1545	5.0736	3.2074
Stretch-bend	0.6380	0.5273	0.5446	0.4881
Torsion	12.2883	9.4263	8.8060	7.2987
Non-1,4 VDW	-7.3250	-7.4292	-7.0929	-8.1595
1,4 VDW	10.3901	10.0688	9.6343	9.8116
Dipole-dipole	-6.3522	-6.3296	-6.5306	-5.1946
TOTAL	19.3851	13.1050	11.9574	8.9948

As seen above, the most stable conformations of the two isomers are ones where the amide group is equatorial. This can be attributed to that fact that there is less 1, 3 di-axial interactions is these conformations. Furthermore as seen above, the trans decalin isomer is more energetically stable than cis decalin as the OH group is axial in cis decalin. In order to provide reasoning for the different rates of hydroylsis of the two isomers the 3D- structures of the isomers were analyzed. As the hydroylsis of a peptide bond involves the attack of the lone pair oxygen( alcohol group) on the carbonyl carbon, the distance between these atoms was measured and then the angle between them was measured:

	13 ,amide axial	13, amide equatorial	14, amide axial	14, amide equatorial
Angle of approach(o)	65.7	74.3	66.9	59.5
Distance(Ao)	2.98	2.80	2.94	3.07

Ideally one would expect that the angle of approach of the OH nucleophile to the C=O would be close to the Burgi-Dunitz angle ( 107^o) as this would lead to the greatest overlap between the sp³lone pair oxygen and the C=O π* orbital.

Isomer 13 By analysis of the 3D structure of the amide equatorial conformer of 13 it can be seen that the C=O group requires less rotation than the amide axial conformer to allow for the OH group to attack at the Burgi-Dunitz angle(107 o). In this isomer this rotation is possible due to the fact that the cis junction between rings make the isomer more flexible. As a result, the major conformer of 13 is also the most reactive and thus accounts for the fast reaction rate.

Isomer 14 For isomer 14, analysis of the 3D structure shows how the amide axial conformer of 14 allows for the OH group to attack at an angle closest to the Burgi-Dunitz angle and in fact, as confirmed in literature, this conformer is the only conformer which can react. This can be attributed to the fact that the trans junction between the rings make the structure extremely rigid therefore rotation in the molecule and ring flipping between conformers is also not easily possible. As the reactive conformer is the minor conformer this results in a slower reaction rate

Regioselective addition of Dichlorocarbene

In order to illustrate orbital control of reactivity, the reaction of the below compound with the electrophilic reagents dichlorocarbene was studied:

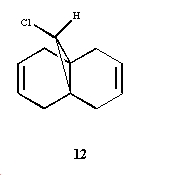
In order to predict the geometry of the above it was first optimized using the MM2 method and then further optimized using the HF/STO-3G MO method and lastly the B3LYP/6-31G(d) approach and the results are reported below:

MM2	HF/STO-3G	B3LYP/6-31G(d)
Compound5	Compound5	Compound5

As you can see above that the difference in the 3 models is the orientations of the cyclohexene rings The MM2 method outputs a geometry where the two cyclohexene rings have identical geometries whereas in the HF/STO-3G the cyclohexene ring endo to the C-Cl bond is flattened slightly and in the B3LYP/6-31G9(d) this endo ring is flattened even more. These differences in the calculation methods were quantified by looking at the angle of the C-Cl bond to the plane of the triclycic ring as seen below:

Method	Bond Angle(C-Cl to tricyclic ring)
MM2	107.4o
HF/STO-3G	110.8o
B3LYP/6-31G(d)	111.9o

These differences can be attributed to the fact that the MM2 method only considers the non-bonding lone pair electrons whereas the other two methods considers all electrons.

In order to predict the site of addition of dichlorocarbene, the molecular surfaces of molecule 12 were analyzed. These molecular surfaces were calculated using both the HF/STO-3G method as well as the B3LYP/6-31G9(d) however as the latter is a more accurate depiction these molecular surfaces were analyzed as seen below:

HOMO-1	HOMO	LUMO	LUMO+1	LUMO+2

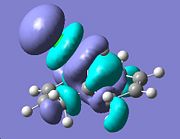The orbital presumed to be involved in electrophilic attack is said to be the HOMO and as seen above as most of the electron density is concentrated on the endo alkene. Furthermore, although this cannot be clearly observed above, as stated in the literature, there is said to be an overlap between the HOMO-1 ( C=C π exo) and the LUMO+2(C-Cl σ* orbital) which would result in the strengthening of the exo cyclohexene bond. As a result of the two findings one would thus expect the endo cyclohexene to be the site of addition of the dichlorocarbene.

Vibrational Spectrum of Diene and Hydrogenated Compound

Structure 12 and the hydrogenated version of 12 ( exo C=C bond) were optimized using the B3LYP/6-31G(d) method again and then their vibrational frequencies were calculated to yield the following results :

Product	v C=C(cm-1)(endo)	v C=C(cm-1)(exo)	v C-Cl(cm-1)
Compound 12	1761.01	1740.9	772.54
Hydrogenated Compound 12	1761.67	N/A	776.88

As seen above the exo C=C stretching frequency is lower than the endo stretching frequency which can be attributed to as mentioned previously the donation of electron density from the exo C=C orbital to the C-Cl σ* orbital. This reasoning also accounts for why there is an increase in the frequency of the C-Cl stretching frequency as in the hydrogenation product as this overlap no longer exists.

Mini Project- Click Chemistry

This experiment involves the 1,3-diploar cycloaddition between an azide and an alkyne which yields two possible regioisomeric products as seen below:

In order to distinguish between the two isomers, they were first minimized by MM2 and then the DFT method to yield the following optimized geometries.

Isomer A	Isomer B
Click A	Click B

The DFT method was then used to calculate the NMR of these isomers to yield the following results:

Isomer A NMR Spectrum	Isomer A Peak List

Isomer B NMR Spectrum	Isomer B Peak List

Difference between experimental and calculated δ(Isomer A)	Difference between experimental and calculated δ(Isomer B)

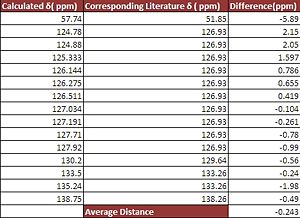
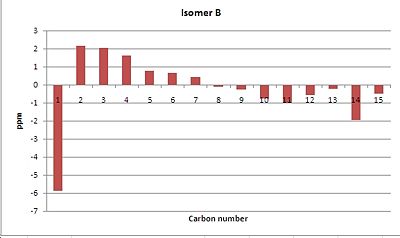
As you can see from above the predicted peaks in the ¹³C NMR are extremely close to the experimental values as seen in literature. From the above the tables and graphs you can see that for isomer A the average difference between the experiment and calculated chemical shift is 0.491ppm with the maximum difference being 2.958ppm. For isomer B this average difference is -0.243ppm with again the maximum difference being -5.89ppm. Furthermore from analysis of the table you can see that there are significantly more calculated peaks than experimental peaks. This can be attributed to the fact that this method distinguishes between each atom unlike the experimental values where carbons in the same environment appear as one peak. Another noticeable difference between the two structures is that the calculated spectrum does not show splitting unlike the experimental spectrum.

The key difference in the spectrums for Isomer A and Isomer B is the chemical shift of the C-H group on the five membered ring structure as in Isomer A, the aromatic groups are in the same plane whereas in Isomer B they are not planar and thus Isomer B is less de-shielded. The corresponding chemical shifts are for Isomer A (145.042, lit 138.26) and Isomer B (138.75,lit,148 ) and thus this model provides an effective way or distinguishing between two isomers.