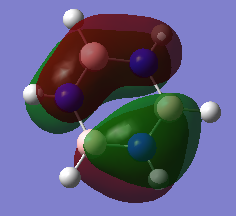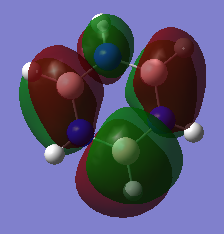Rep:Mod:t3gy216
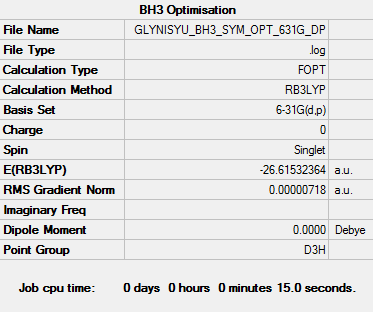
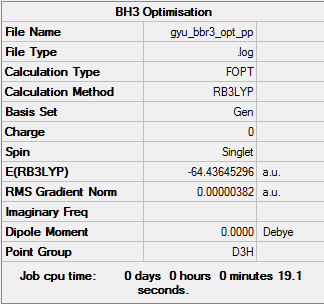
BH3
Calculation Method and Basis Set: B3LYP/6-31G(d,p)
Item Value Threshold Converged? Maximum Force 0.000014 0.000450 YES RMS Force 0.000009 0.000300 YES Maximum Displacement 0.000057 0.001800 YES RMS Displacement 0.000037 0.001200 YES
Frequency Analysis
Frequency analysis log file here
Low frequencies --- -10.0419 -2.9960 -0.0054 0.4925 2.1764 3.7030 Low frequencies --- 1162.9539 1213.1540 1213.1567
Optimised BH3 molecule |
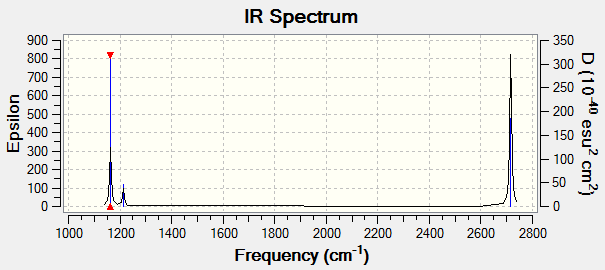
Vibrational spectrum for BH3
| Wavenumber (cm-1) | Intensity (arbitrary units) | Symmetry | IR Active? | Type |
| 1163 | 93 | A2 | Yes | Out-of-plane bend |
| 1213 | 14 | E' | Very slight | Bend |
| 1213 | 14 | E' | Very slight | Bend |
| 2582 | 0 | A1' | No | Symmetric stretch |
| 2716 | 126 | E' | Yes | Asymmetric stretch |
| 2716 | 126 | E' | Yes | Asymmetric stretch |
Although there are 6 vibrations, only 3 show up in the IR spectrum. One of the visible peaks is due to the a2 bend. The a1 stretch is not IR active as there is no change in dipole moment. The last two peaks are due to the e' bends and stretches. As both e' bends and both e' stretches are degenerate, only one peak arises for each set of degenerate bends/stretches.
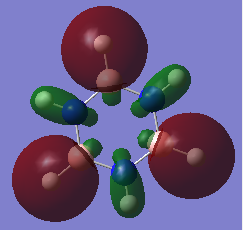
Molecular Orbital Diagram for BH3
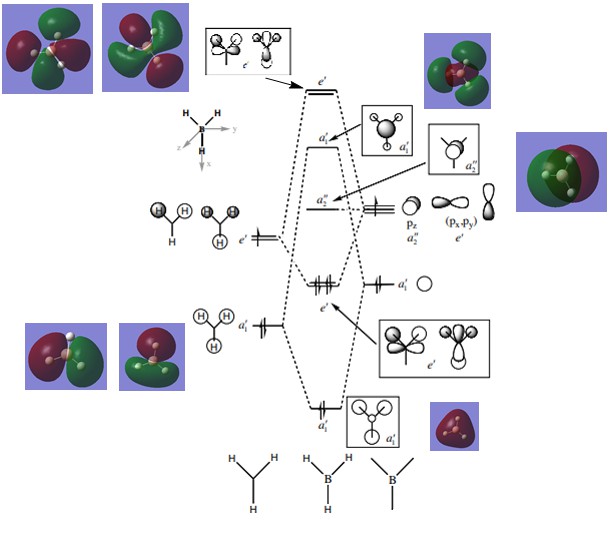[1]
Looking at the diagram shown above, there is resemblance between the real MOs and predicted MOs by LCAO. The predicted MOs accurately depict the shape and phase of the electron distribution shown in the computationally analysed orbitals. This shows that using qualitative MO theory is a useful and accurate way of predicting molecular orbitals.
Ng611 (talk) 18:57, 6 June 2018 (BST) Good MO analysis. Are there any differences at all that you can see?
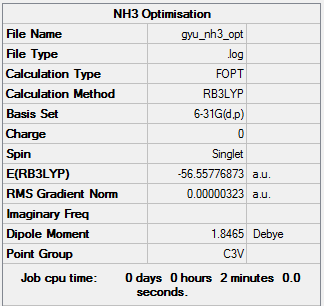
NH3
Calculation method and basis set: B3LYP/6-31G(d,p)
Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000012 0.001800 YES RMS Displacement 0.000008 0.001200 YES
Frequency Analysis
Frequency analysis log file here
Low frequencies --- -8.5646 -8.5588 -0.0041 0.0455 0.1784 26.4183 Low frequencies --- 1089.7603 1694.1865 1694.1865
Optimised NH3 molecule |
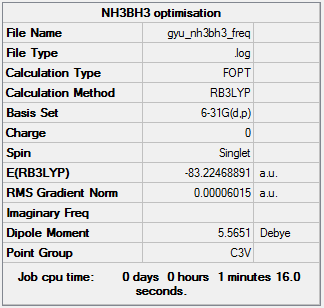
NH3BH3
Calculation method and basis set: B3LYP/6-31G(d,p)
Item Value Threshold Converged? Maximum Force 0.000122 0.000450 YES RMS Force 0.000058 0.000300 YES Maximum Displacement 0.000540 0.001800 YES RMS Displacement 0.000297 0.001200 YES
Frequency Analysis
Frequency analysis log file here
Low frequencies --- -0.0571 -0.0499 -0.0075 21.7150 21.7251 40.6257 Low frequencies --- 266.0444 632.3706 640.1455
Optimised NH3BH3 molecule |
Calculations
| Molecule | Energy (au) |
|---|---|
| BH3 | -26.61532 |
| NH3 | -56.55777 |
| NH3BH3 | -83.22469 |
The bond association energy can be calculated using ΔE=E(NH3BH3)-[E(NH3)+E(BH3)].
ΔE = -83.22469-(-26.61532+-56.55777) = -0.0516 au
In kJmol-1, the bond association energy comes out to be -135 kJmol-1
The calculated bond dissociation energy for the B-N dative bond is 135 kJmol-1. Comparison to the bond dissociation energy of a Br-Br bond (192 kJmol-1) indicates that the B-N bond is weak, as the dissociation energy is even smaller than that for Br-Br[1].
Ng611 (talk) 18:58, 6 June 2018 (BST) Good calculation. Wikipedia is not a good reference however. Ideally, cite something peer reviewed.
BBr3
Calculation method and basis set: B3LYP/6-31G(d,p)
Item Value Threshold Converged? Maximum Force 0.000008 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.000036 0.001800 YES RMS Displacement 0.000023 0.001200 YES
Frequency Analysis
Frequency Analysis log file here
Low frequencies --- -0.0137 -0.0064 -0.0046 2.4315 2.4315 4.8421 Low frequencies --- 155.9631 155.9651 267.7052
Optimised BBr3 molecule |
Link to Dspace: http://hdl.handle.net/10042/202448
Project Section: Aromaticity
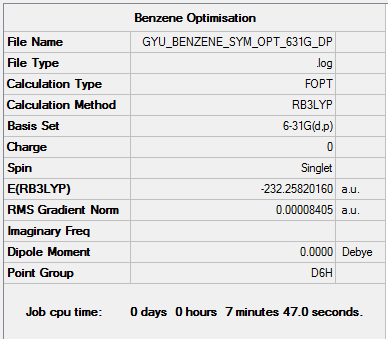
Benzene
Calculation method and basis set: B3LYP/6-31G(d,p)
Item Value Threshold Converged? Maximum Force 0.000194 0.000450 YES RMS Force 0.000077 0.000300 YES Maximum Displacement 0.000824 0.001800 YES RMS Displacement 0.000289 0.001200 YES
Frequency Analysis
Frequency Analysis log file here
Low frequencies --- -2.1456 -2.1456 -0.0087 -0.0042 -0.0041 10.4835 Low frequencies --- 413.9768 413.9768 621.1390
Optimised Benzene molecule |
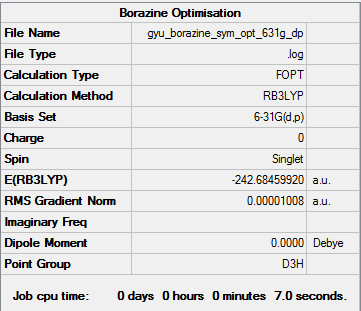
Borazine
Calculation method and basis set: B3LYP/6-31G(d,p)
Item Value Threshold Converged? Maximum Force 0.000011 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.000065 0.001800 YES RMS Displacement 0.000021 0.001200 YES
Frequency Analysis
Frequency analysis log file here
Low frequencies --- -13.9554 -13.7954 -10.4509 -0.0104 -0.0091 0.0726 Low frequencies --- 289.0422 289.0509 403.8550
Optimised Borazine molecule |
Benzene vs. Borazine
Charge Distribution
| Benzene | Borazine |
|---|---|
 |
|
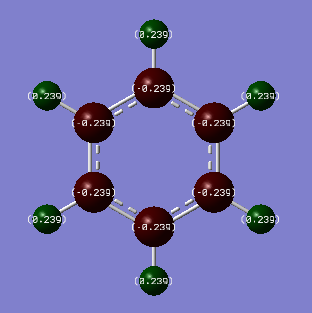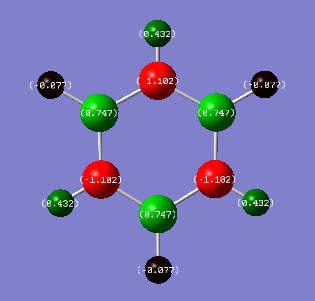
| Carbon Charge: -0.239 | Boron Charge: 0.747 |
| Hydrogen Charge: 0.239 | Nitrogen Charge: -1.102 |
| - | Hydrogen Charge (bonded to B): -0.077 |
| - | Hydrogen Charge (bonded to N): 0.432 |
In benzene, more electron density is located around the carbon atoms (-0.239) than the hydrogen atoms (0.239). This can be reasoned by comparing their relative electronegativities. Using the Pauling scale, carbon has a higher electronegativity (2.55) than hydrogen (2.20) and the values for the charge distribution of benzene reflects this; carbon has a negative charge distribution whilst hydrogen has a positive one. As benzene is symmetrical, all of the carbon atoms have the same electron distribution around them, as do the hydrogen atoms.
Unlike in benzene, the charge distribution around borazine is not symmetrical. (Ng611 (talk) 19:00, 6 June 2018 (BST) It's still symmetric -- just 3-fold symmetric instead of 6-fold.) The same argument of electronegativites can be used to explain this. From the elements in borazine, nitrogen has the largest electronegativity (3.04). When looking at the charge distribution of borazine above, the nitrogen atoms have the most negative values (-1.102), and so have the most electron density surrounding them. Boron has an electronegativity of 2.04. These boron atoms are located in between nitrogen atoms, therefore the charge distribution around boron is 0.747 as nitrogen is more electronegative, drawing electron density away from the boron atoms. The hydrogen atoms have different electron density around them, which depends on whether they are bonded to nitrogen or boron. The H atoms attached to boron have a negative value for charge distribution because hydrogen has a larger electronegativity than boron (2.20 to 2.04). The hydrogens attached to nitrogen have a positive charge distribution as nitrogen has a much greater electronegativity than hydrogen (3.04 to 2.20).
Ng611 (talk) 19:00, 6 June 2018 (BST) Good discussion of the effects of electronegativity on the overall charge distribution. What do the partial charges sum to, and is there any difference in partial charge for atoms related by symmetry?
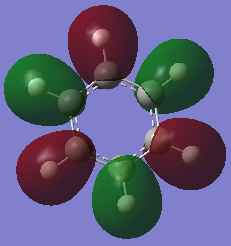
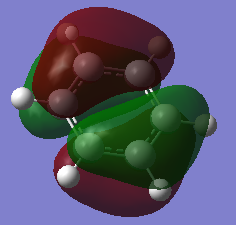
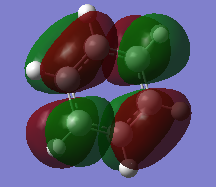
Molecular Orbital Comparison
| Benzene MO | Borazine MO | Description |
|---|---|---|
 |
 |
Benzene MO13, Borazine MO16: These orbitals are similar in that they are both σ-antibonding MOs however, they differ in that they have different contributions from atoms. As benzene has D6h symmetry, the orbital contributions of each carbon and hydrogen is symmetric. However, in borazine the boron atoms have larger lobes since they have a lower electronegativity, contributing more to the antibonding orbitals than the nitrogen atoms (smaller lobes). |
 |
 |
HOMO MO 21: The HOMO of benzene and borazine are very similar and are both π-bonding MOs with a node running through the middle. The main difference being that the benzene HOMO is entirely symmetric, whereas the borazine HOMO is skewed due to the difference in electronegativities of boron and nitrogen. Nitrogen has a higher electronegativity so there is a more concentrated area at the nitrogen atom, as it contributes more to the bonding orbital. |
 |
 |
LUMO MO 22: Both of the LUMOs are π-antibonding MOs. Benzene has an equal orbital distribution across the molecule as it's symmetric however, borazine has a larger contribution to the antibonding orbital from the boron atoms due to having a lower electronegativity and therefore a higher energy. |
Ng611 (talk) 19:01, 6 June 2018 (BST) Well done for comparing the correct MOs by shape and not energtic ordering (which is not necessarily reliable). I would include a brief discussion of the overall symmetry of the molecule to improve this section further. Perhaps also consider dicussing the constituent AOs that form the MOs and the overall symmetry/character of the MO.
Aromaticity
The term aromaticity is typically used to describe organic molecules which are cyclic, planar and have unusual stability due to resonance compared to molecules with the same set of atoms and arrangement.[1]
Typically, Huckel's Rules can be used to determine whether a molecule would be aromatic or not. The rules are as followed:
1. they must be planar
2. they must form a ring (i.e. are cyclic)
3. they have a continuous ring of p-orbitals
4. they have 4n+2 π-electrons, where n is an integer
Aromaticity was first associated with benzene however, since then it has been found that Huckel's Rules are not always obeyed for molecules to exhibit aromaticity. For example, pyrenophanes have aromatic behaviour however, are non-planar[2]. Likewise, benzene at 20K in its crystalline state adopts a chair conformation, deviating away from its typical planar state[2]. This becomes an issue when associating molecules being planar and the overlapping of pz orbitals, with aromatic behaviour.
Real MOs can be related to the concept of aromaticity as the electrons are described as existing within the molecular orbitals, enabling delocalisation across all the atoms rather than existing as electron pairs on individual atoms. In benzene, the electron distribution across the molecule is spread out evenly due to its symmetry however, the electron distribution of borazine would be skewed as the different atoms have different electronegativies and thus energies, meaning they contribute differently towards the molecular orbitals.
When looking at the real MOs calculated for benzene, we observe that not all of the MOs are made up from π-orbitals, there is contribution from σ-orbitals towards the special properties of aromatics as well. Looking into the importance of these σ-electrons has recently been a topic of discussion among researchers. For example, H6 when constrained to D6h symmetry shows benzene-like aromatic characteristics which cannot be explained by the overlapping of p-atomic orbitals, as hydrogen does not have accessible p-atomic orbitals. Instead, the behaviour of H6 can be attributed to the delocalisation of the 6-electrons (4n + 2) in σ-orbitals[3]. This is known as σ-aromaticity.
Ng611 (talk) 19:04, 6 June 2018 (BST) Interesting second paragraph. σ-aromaticity is a good example of a more modern and informed approach to aromaticity, what other modern aromatic phenomena are there? Overall this is a good section, but you should expand on the points you made.
Ng611 (talk) 19:05, 6 June 2018 (BST) A very good report. Remember to take your time and be as thorough with your answers as possible!
- ↑ https://en.wikipedia.org/wiki/Aromaticity
- ↑ 2.0 2.1 Palusiak, M, Krygowski, T.M., Chem. Eur. J. 2007, 13, 7996 – 8006
- ↑ Li, Z.H., Moran, D, Fan, K.N., von Rafue Schleyer, P, J. Phys. Chem. A 2005, 109, 3711-3716