Rep:Mod:szd2810
introduction
In this study Gaussview is used to simulate a varitey of inorganic molecules and to the then probe them using a variety of basis sets and methods. the NBO's and MO's of the molecules where also investigated. Gaussview would then give predicted information on the molecules bonds and its IR's, along with any bonding interactions.
BH3
optimistation of the bond lengths in BH3
The bond lengths of the intial generated molecule where changed to 1.500A from the intal value of 1.18A
basis set 3-21G
The BH3 molecule was then optimized using the following method illustrated
| method | ground state | DFT | default spin | B3LYP |
|---|---|---|---|---|
| basis set | 3-21G | -- | -- | -- |
| charge | 0 | spin | singlet | -- |
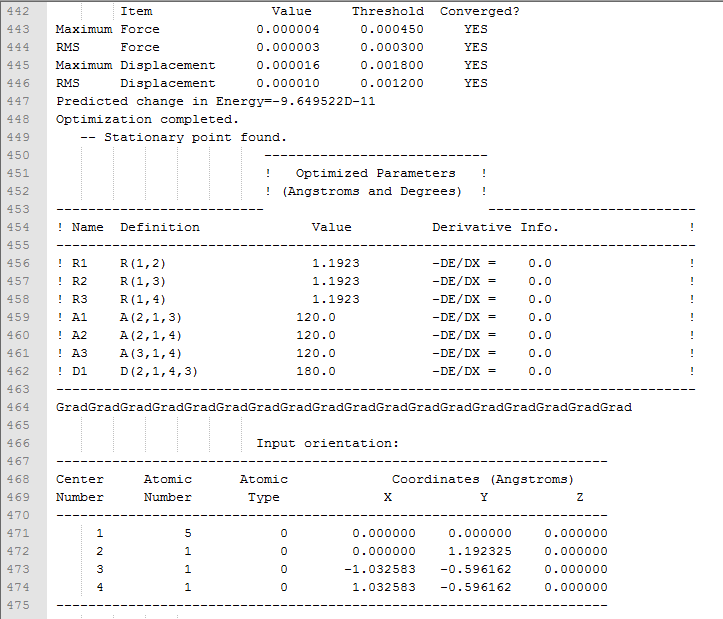
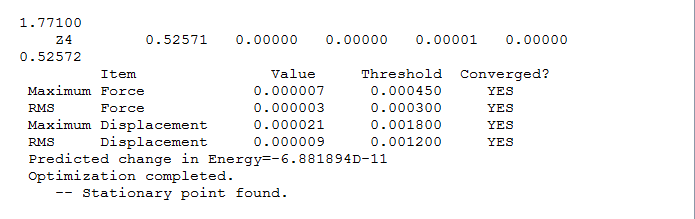
B-H bond distance before the optimization = 1.500A B-H distance after optimization method = 1.194539A the bond angle remained constant throughout the optimization = 120.0000
| file name | BH3_optimisation |
| file type | .chk |
| calculation type | FOPT |
| calculation method | RB3LYP |
| basis set | 3-21G |
| charge | 0 |
| spin | singlet |
| total energy | -26.46226433 a.u. |
| rms gradient | 0.00004507 a.u. |
| imaginary freq | |
| dipole moment | 0.000 debye |
| point group | -- |
File:BH3 summary.txt - this is a link to the above table

File:BH3 optimisation note pad.txt - link to the original convergence document
basis set 6-31G
The molecule was further optimized via the 6-31G basis as this is a higher level basis and hence a better overall basis
| method | Ground state | DFT | default spin | B3LYP |
|---|---|---|---|---|
| basis set | 6-31G | d | p | |
| charge | 0 | spin | singlet |
B-H bond distance before the optimization = 1.19453A B-H bond distance after the 6-31G optimization method = 1.19231A
the bond angle renamed constant throughout the optimization
| File name | BH3 optimisation 6-31G |
|---|---|
| file type | .chk |
| calculation type | FOPT |
| file type | FOPT |
| calculation method | RB3LYP |
| basis set | 6-31G (d,p) |
| charge | 0 |
| spin | singlet |
| total energy | -26.61532225 a.u. |
| RMS gradient norm | 0.00024090 a.u. |
| imaginary frequency | -- |
| dipole moment | 0.0000 debye |
| point group | D3h |
| Job cpu time | 0 days 0 hours 0 minutes 4.0 seconds. |
File:BH3 optimisation 6-31g summary.txt - link to the above table
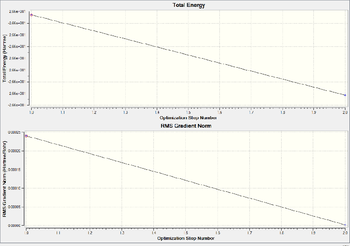
frequency analysis of BH3
| orbital number | visulisation |
|---|---|
| 1 | 
|
| 2 | 
|
| 3 | 
|
| 4 | 
|
| 5 | 
|
| 6 | 
|
| 7 | 
|
| 8 | 
|
virational modes of BH3
TlBr3
TlBr3 optimisation
the TlBr3 molecule was simulated on Gaussview with tight symmetry restrictions of a tolerance of 0.0001 then optimisied under these restrictions using a LanL2DZ basis
| method | ground state | DFT | default spin | B3LYP |
|---|---|---|---|---|
| basis set | LanL2DZ | |||
| charge | 0 | spin | singlet |
| file name | BH3_optimisation |
| file type | .chk |
| calculation type | FOPT |
| calculation method | RB3LYP |
| basis set | LANL2DZ |
| charge | 0 |
| spin | singlet |
| total energy | -91.21812851 a.u. |
| rms gradient | 0.00000090 a.u. |
| imaginary freq | |
| dipole moment | 0.000 debye |
| point group | -- |
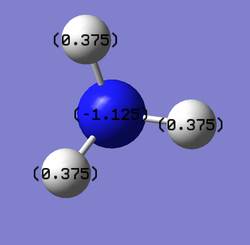
Tl-Br bond distance before the optimization = xxxxx Tl-Br bond distance after the optimization = 2.65095A
the bond angle remained constant throughout the optimization
TlBr3 frequency analysis
https://spectradspace.lib.imperial.ac.uk:8443/dspace/handle/10042/23582 - this is the link to the completed BBr3 optimization file
TlBr3 vibrational analysis
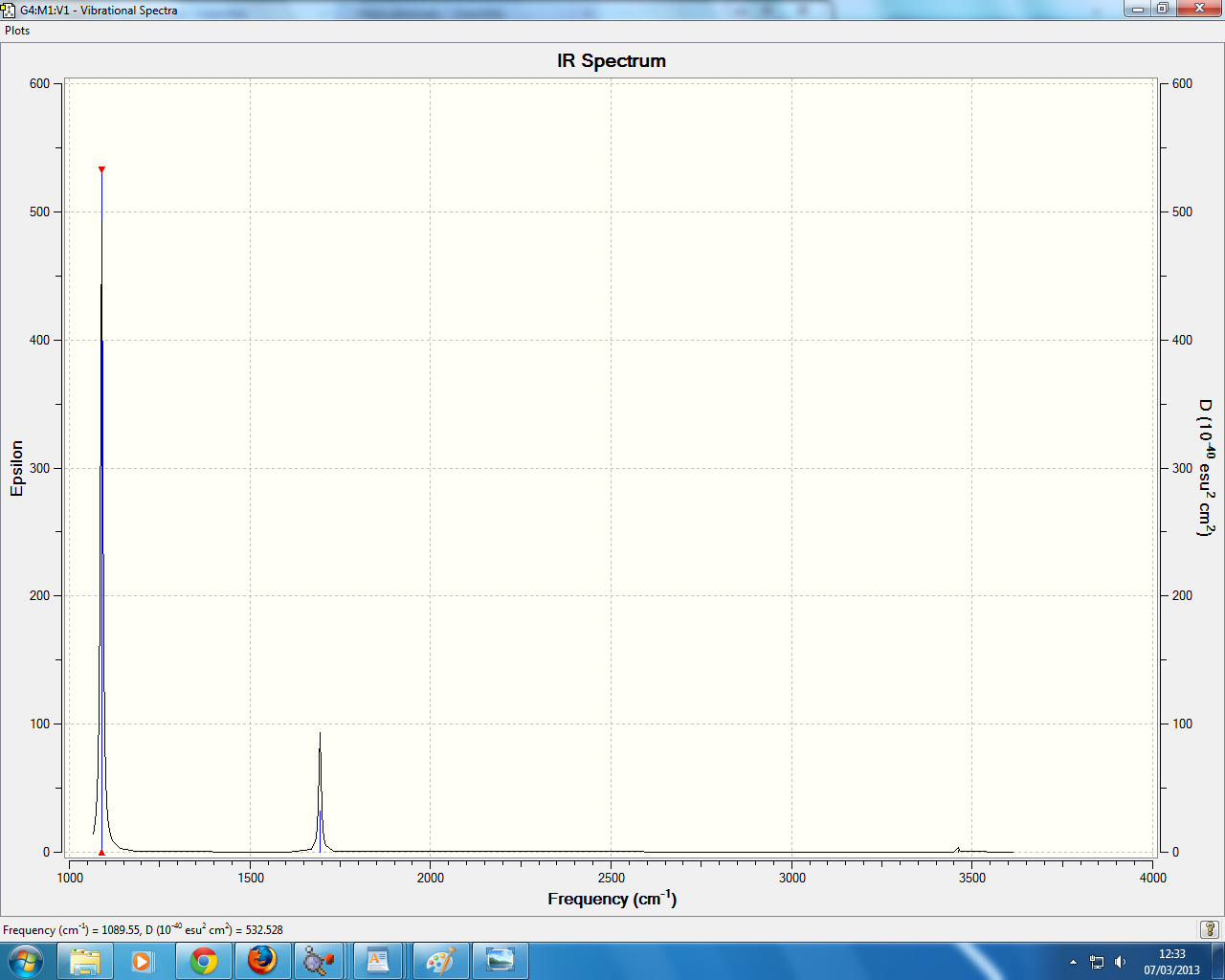
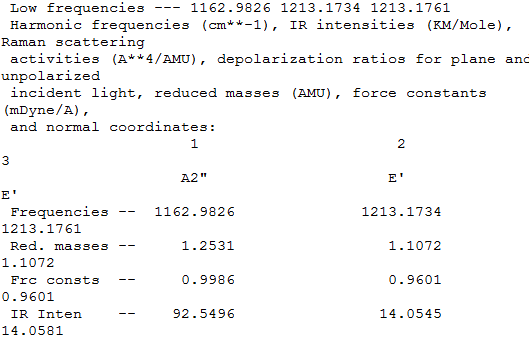
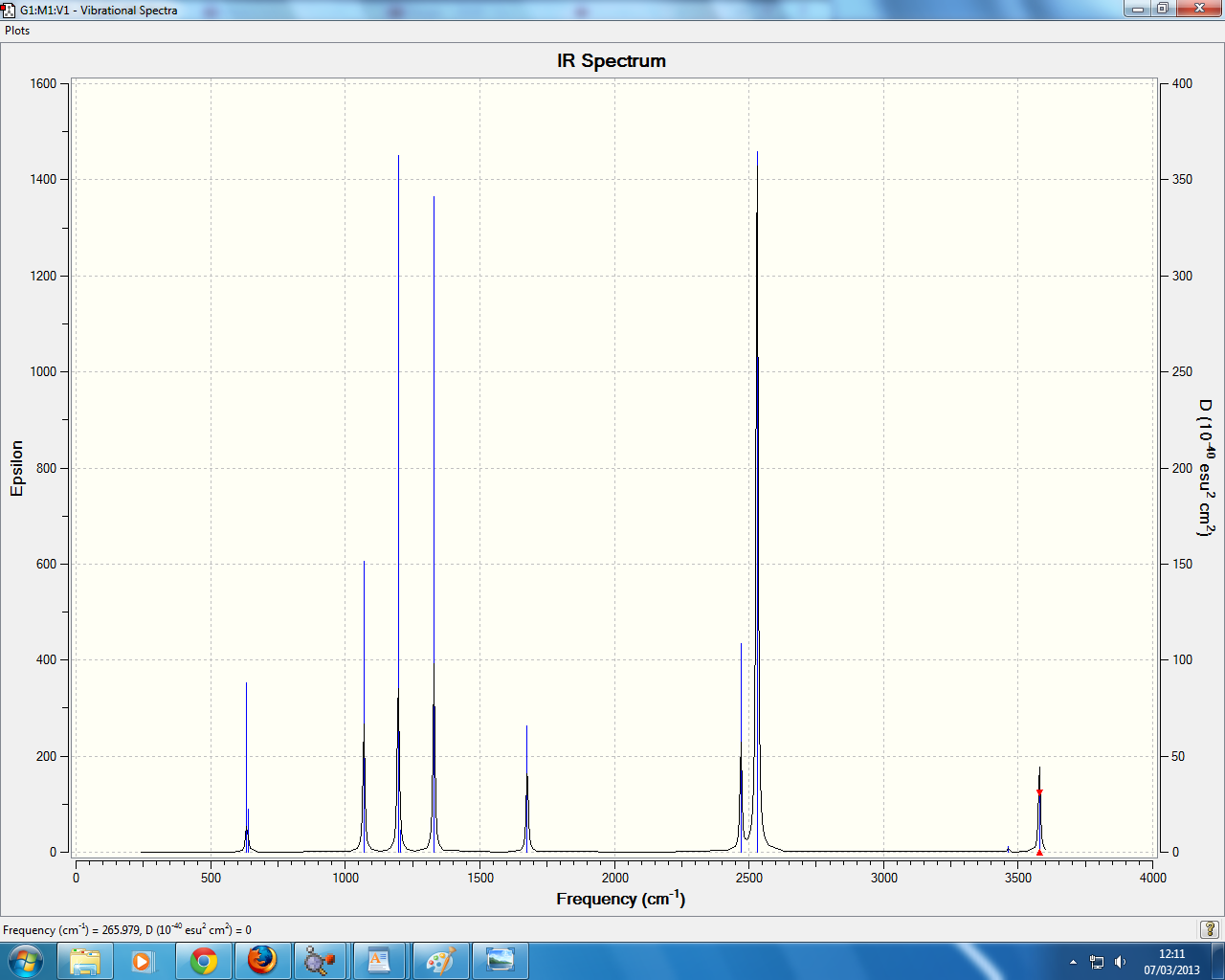
3 peaks are seen since only 5 are ir active with 4 being degenerate. mode 4 isnt active since it has no dipole moment
BBr3
bond length before optimisation = 2.0000A
bond length after optimisation = 1.93396A
BBr3 optimisation
to determine if the optimisation of the BBr3 molecule was correct a frequency analysis of the molecule must be undertaken
B-Br bond length = 1.19231 bond angle remained constant throughout analysis at 1200
| file type | .log |
| calculation type | FOPT |
| calculation method | RB3LYP |
| basis set | Gen |
| charge | 0 |
| spin | singlet -64.43645296 a.u. |
| total energy | 0.00000382 a.u. |
| RMS gradient norm | |
| dipole moment | 0.0000 Debye |
| point group | D3H |
| job cpu time | 0 days 0 hours 0 minutes 10.0 seconds. |
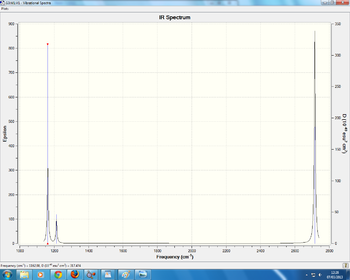
this was taken from the frequency analysis and shows that the molecule was correctly optimized since the low frequency is XXXX. it is also seen that the molecule has been optimized to a minimum due to the presence of a energy minima.
BBr3 frequency analysis
in the IR spectrum 3 peaks are visible, though there are predicted 6 peaks. the reason for this is only 5 of the modes are IR active with the with the other 2 modes being degenerate. the mode NUMBER is also inactive since is doesnt have a dipole moment, with the final modes NUMBERS having the same symmetry (E') and hence seen as one peak due to them being degenerate.
https://spectradspace.lib.imperial.ac.uk:8443/dspace/handle/10042/23582 - this is the link to the completed BBr3 optimization file
comparison of BH3 BBr3 and TlBr3
comparison of BH3 BBr3 and TlBr3 bondlengths
| molecule | bond length (A) |
|---|---|
| BH3 | 1.19231 |
| BBr3 | 1.93396 |
| TlBr3 | 2.65095 |
the bond length orders are then seen (with decreasing value) TlBr3,BBr3,BH3 BH3 is smaller than BBr3 due to the smaller atomic radii of the H atom compared to Br, with a value of 53ppm compared to 120ppm. this means a larger molecule since the central Boron atom doesn't change in atomic radii. both molecules are bonded covalently, though the presence of the lone pairs on bromine allows for donation into the orthogonal P orbital of the boron atom. this would consequently shorten the B-Br bond since there is better overlap between the orbitals, however this decrease in bond length is relatively small compared to the increased size due to the bromine being a larger atom.
the increased size of the TlBr3 atom compared to the BBr3 molecule is due to the increased size of the central atom (since in this case it is the bromine atoms that stay constant in atomic radii length B=90ppm Tl=190ppm). it is the increase in size of the Tl orbitals (S and P) that result in a poorer overlap in the Tl-Br bond compared to the B-Br bond. as with before both bonds are also covalent.
The gaussview program however will form bonds between 2 atoms if the bond distance is small enough for orbital interactions. this will sometimes result in the formation of bonds in gaussview that wouldn't be expected, since bonds are the interaction between two (or more is relevant)atoms and their filled bonding orbitals. however gaussviews definition of bonds are the interaction between electrons and atoms, not filled bonding orbital interactions.
BH3 BBr3 and TlBr3 vibrational modes comparison
the use of the 6-31G basis gives a more accurate potential energy of the molecules surface. This is due to the basis being a larger set. since different energy potentials of the molecules surfaces mean that a comparison cannot be undertaken, and give respectable and fair results, different methods of optimizations will give different potentials. This will mean the energy minima will be nonequivalent for the two differing optimized molecules. this is why frequency analysis is used, since it will allow us to see whether or not the molecule was correctly optimized.
the reason that the BBR3 AND TLBr3 molecule have much lower values is since they are much more massive than the BH3 molecule and this means that their reduced mass will much greater in turn lowering the wavenumbers. the poorer overlap of orbitals between the B-Br bond and Tl-Br bonds also accounts for them being weaker than the B-H bond, and this is seen by the Tl-Br bond being much longer than the others, with the B-H bond being much shorter.
all the molecules have 3 IR peaks with 5 peaks being IR active, with 2 degenerate E' modes 1 inactive A' mode and one A2" mode, with the E' and A' mode being relatively simular in energy.
inserts.
both the molecules have D3h symetry labels and hence are triagonal plance, so using the 3N-6 rule this gives 6 modes of vibration. since the energies of the symmerteies are the same (this is seen by the equal intesities and frequencyts for the symmerty) the modes of vibration are equal. the molecules all have 3 peaks as explained by the 5 modes being active with the symmetry labels of E,A'1 and A"2. since the B-H bonds are shorter than the Tl-Br bonds due to better orbital overlap the BH3 molecule has a larger range of motions relative to the TlBr3 molecule since the B-H bonds are stronger.
since the B-H bonds are shorter, a larger energy is needed for the same vibrational energy to result in a equivelent motion. this is seen by the frequencts for the intensties of the same symmerty vibrations are of a higher value for the BH3, relative to TlBr3.
since the Tl and Br atoms have larger more diffuse electron clouds thhis means the intensites are much lower for the TlBr3 molecule with the peaks in the same place (relatively) for the two molecules.
the A'1 and E' are both strech motions and these are of a higher energy than the scissorting and wagging motions of the E and A"2. this explains why the A"2 and E' vibrations are similar and the E' and A'1 vibrations are close. the reason for the larger energy of the stretches is because they require a change of electron density.
as the mode number increases the frequency is also seen to increase for both molecules, though due to the increased mass difference between the Tl and Br relative to B and H this makes the A"2 labelled mode more energic reltive to the E', for the TlBr3 molecule. this accounts for the movement of the central atom in the molecule.
NH3 molecule
the ammonia molecule was optimised using gaussview to generate an optimised molecule with a changed bond lenth
N-H bond distance before the optimization = 1.0000A N-H bond distance after the 6-31G optimization method = 1.01797A
the bond angle renamed constant throughout the optimization

| File name | BH3 optimisation 6-31G |
|---|---|
| file type | .chk |
| calculation type | FOPT |
| file type | FOPT |
| calculation method | RB3LYP |
| basis set | 6-31G (d,p) |
| charge | 0 |
| spin | singlet |
| total energy | -56.55776856 a.u. |
| RMS gradient norm | 0.00000885 a.u. |
| imaginary frequency | -- |
| dipole moment | 1.8464 Debye |
| point group |
frequency analysis
vibrational analysis of NH3
Nh3_8.png
NH3 orbitals
| orbital number | visulisation |
|---|---|
| 1 | 
|
| 2 | 
|
| 3 | 
|
| 4 | 
|
| 5 | 
|
| 6 | 
|
NH3 charge distribution
NH3BH3
optimisation
| File name | NH3BH3_optimisation |
|---|---|
| file type | .chk |
| calculation type | FOPT |
| file type | FOPT |
| calculation method | RB3LYP |
| basis set | 6-31G (d,p) |
| charge | 0 |
| spin | singlet |
| total energy | -83.22468918 a.u. |
| RMS gradient norm | 0.00006806 a.u. |
| imaginary frequency | -- |
| dipole moment | 5.5655 Debye |
frequency analysis
| File name | NH3BH3_optimisation | ||
|---|---|---|---|
| 1 | 265.98 | 0.000 | A |
| 2 | 632.38 | 13.9923 | A |
| 3 | 639.08 | 3.5550 | A |
| 4 | 640.21 | 3.5556 | A |
| 5 | 1069.12 | 40.4878 | A |
| 6 | 1069.58 | 40.5609 | A |
| 7 | 1169.58 | 108.8541 | A |
| 8 | 1203.63 | 3.5164 | A |
| 9 | 1203.96 | 2.4878 | A |
| 10 | 1329.72 | 113.7031 | A |
| 11 | 1676.2 | 27.5551 | A |
| 12 | 1676.32 | 27.5393 | A |
| 13 | 2470.21 | 67.2475 | A |
| 14 | 2530.04 | 231.3619 | A |
| 15 | 2530.30 | 231.3495 | A |
| 16 | 3462.41 | 2.5098 | A |
| 17 | 3579.19 | 27.9254 | A |
| 18 | 3579.27 | 27.9208 | A |
energy of association of NH3 and BH3 molecule
E of BH3 = -26.4623 E of NH3 = -56.5578 E of NH3BH3 = -83.2247
change in energy = E of NH3BH3 - [(E OF NH3) +E of BH3)] = -0.02439a.u since 1 a.u = 2625.5 kjmol-1 enthalpy of formation = 64.035945
aromacity
this was futher investigatied using aromatic cmpaunds as a basis
benzene
| File name | benzene_optimisation |
|---|---|
| file type | .chk |
| calculation type | FOPT |
| file type | FOPT |
| calculation method | RB3LYP |
| basis set | 6-31G (d,p) |
| charge | 0 |
| spin | singlet |
| total energy | -232.25820551 a.u. |
| RMS gradient norm | 0.00009549 a.u. |
| imaginary frequency | -- |
| dipole moment | 0.0001 Debye |
| Point Group | C1 |
| Job cpu time | 0 days 0 hours 1 minutes 7.0 seconds. |
frequency analysis
IR analysis
| File name | benzene_optimization | |
|---|---|---|
| 1 | 0.0000 | 2 opposite H pairs wagging in and out of the plane alternating |
| 2 | 0.0000 | 2 opposite H pairs wagging in and out of the plane alternating |
| 3 | 0.0000 | c-c bond bending into the plane |
| 4 | 0.0000 | c-c bond bending into the plane |
| 5 | 74.2532 | c-h wagging in and out of the plane |
| 6 | 0.0000 | 2 opposite H pairs wagging in and out of the plane alternating |
| 7 | 0.0000 | 2 opposite H pairs wagging in and out of the plane alternating |
| 8 | 0.0000 | 2 opposite H pairs wagging in and out of the plane alternating |
| 9 | 0.0000 | 2 opposite H pairs wagging in and out of the plane alternating |
| 10 | 0.0000 | 2 opposite H pairs wagging in and out of the plane alternating |
| 11 | 0.0000 | c-h wagging in and out of the plane |
| 12 | 0.0000 | c-c bond stretching into the plane (asymmetric and alternating) |
| 13 | 0.0000 | c-c bond stretching into the plane (asymmetric) |
| 14 | 3.3878 | c-c bond stretching into the plane (asymmetric) |
| 15 | 3.3878 | c-c bond stretching into the plane (asymmetric) |
| 16 | 0.0000 | c-c bond bending into the plane (asymmetric) |
| 17 | 0.0000 | 2 opposite H pairs wagging in and out of the plane alternating (asymmetric) |
| 18 | 0.0000 | c-c bond bending into the plane (asymmetric) |
| 19 | 0.0000 | c-c bond stretching into the plane (asymmetric) |
| 20 | 0.0000 | c-c bond bending into the plane (asymmetric) |
| 21 | 6.6362 | c-c and c-h bond stretching into the plane (alternating) |
| 22 | 6.6274 | c-c and c-h bond stretching into the plane (alternating) |
| 23 | 0.0000 | c-c stretching into the plane (asymmetric alternating) |
| 24 | 0.0000 | c-c stretching into the plane (asymmetric alternating) |
| 25 | 0.0030 | c-h stretching into the plane |
| 26 | 0.0001 | 2 opposite H pairs stretching into the plane (asymmetric) |
| 27 | 0.0001 | 2 opposite H pairs stretching into the plane (asymmetric alternating) |
| 28 | 46.6015 | 2 opposite H pairs stretching (asymmetric alternating) |
| 29 | 46.5711 | 3 C-H stretching (half of the ring) into the plane |
| 30 | 0.0003 | All 6 C-H stretching (symmetrically) |
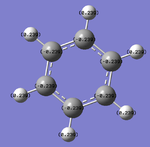
charge distribution
orbital analysis
| orbital number | visulisation |
|---|---|
| 1 | 
|
| 2 | 
|
| 3 | 
|
| 4 | 
|
| 5 | 
|
| 6 | 
|
| 7 | 
|
| 8 | 
|
| 9 | 
|
| 10 | 
|
| 11 | 
|
| 12 | 
|
| 13 | 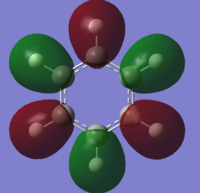
|
| 14 | 
|
| 15 | 
|
| 16 | 
|
| 17 | 
|
| 18 | 
|
| 19 | 
|
| 20 | 
|
| 21 | 
|
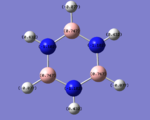
boratabenzene
optimisation
| File name | benzene_optimisation |
|---|---|
| file type | .chk |
| calculation type | FOPT |
| file type | FOPT |
| calculation method | RB3LYP |
| basis set | 6-31G (d,p) |
| charge | -1 |
| spin | singlet |
| total energy | -219.02052962 a.u |
| RMS gradient norm | 0.00016251 a.u. |
| imaginary frequency | -- |
| dipole moment | 2.8446 Debye |
| Point Group | C1 |
| Job cpu time | 0 days 0 hours 1 minutes 7.0 seconds. |
frequency analysis
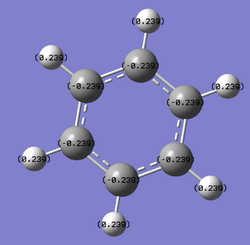
charge distribution
orbital analysis
| orbital number | visulisation |
|---|---|
| 7 | 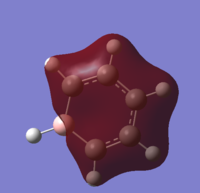
|
| 8 | 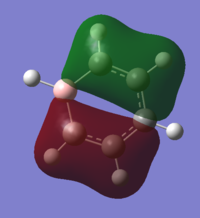
|
| 9 | 
|
| 10 | 
|
| 11 | 
|
| 12 | 
|
| 13 | 
|
| 14 | 
|
| 15 | 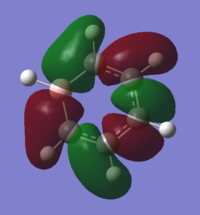
|
| 16 | 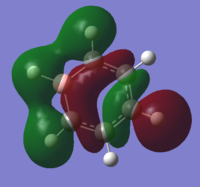
|
| 17 | 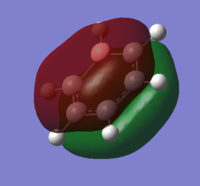
|
| 18 | 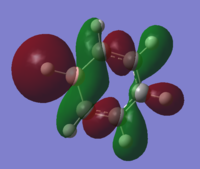
|
| 19 | 
|
| 20 | 
|
| 21 | 
|
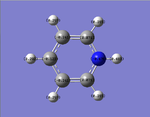
pyridinium
optimisation
| File name | benzene_optimisation |
|---|---|
| file type | .chk |
| calculation type | FOPT |
| file type | FOPT |
| calculation method | UB3LYP |
| basis set | 6-31G (d,p) |
| charge | 1 |
| spin | singlet |
| total energy | -248.66807401 a.u. |
| RMS gradient norm | 0.00002449 a.u. |
| imaginary frequency | -- |
| dipole moment | 1.8724 Debye |
| Point Group | C1 |
| Job cpu time | 0 days 0 hours 13 minutes 12.0 seconds. |
frequency analysis
charge distribution
orbitals analysis
| orbital number | visulisation |
|---|---|
| 7 | 
|
| 8 | 
|
| 9 | 
|
| 10 | 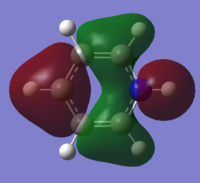
|
| 11 | 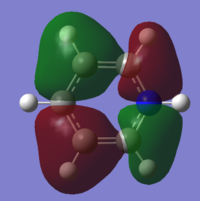
|
| 12 | 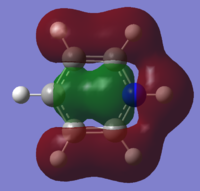
|
| 13 | 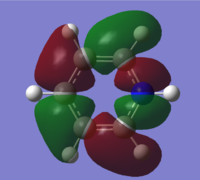
|
| 14 | 
|
| 15 | 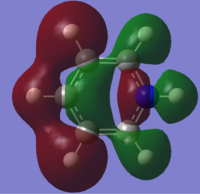
|
| 16 | 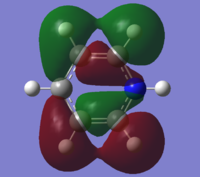
|
| 17 | 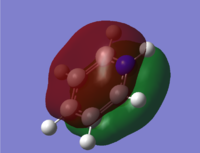
|
| 18 | 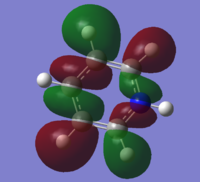
|
| 19 | 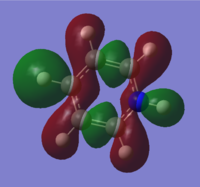
|
| 20 | 
|
| 21 | 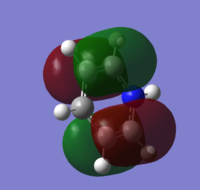
|
borazine
optimisation
| File name | benzene_optimisation |
|---|---|
| file type | .chk |
| calculation type | FOPT |
| file type | FOPT |
| calculation method | RB3LYP |
| basis set | 6-31G (d,p) |
| charge | 1 |
| spin | singlet |
| total energy | -242.68459789 a.u. |
| RMS gradient norm | 0.00007128 a.u. |
| imaginary frequency | -- |
| dipole moment | 0.0003 Debye |
| Point Group | C1 |
| Job cpu time | 0 days 0 hours 2 minutes 37.0 seconds. |
the borazines N-B bond length is longer than a B=N bond yet shorter than a B-N bond indicating delocalisation across the bond
frequency analysis
charge distribution
orbital analysis
| orbital number | visulisation |
|---|---|
| 7 | 
|
| 8 | 
|
| 9 | 
|
| 10 | 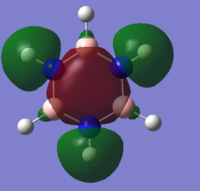
|
| 11 | 
|
| 12 | 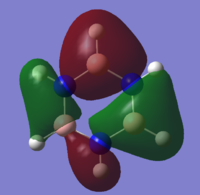
|
| 13 | 
|
| 14 | 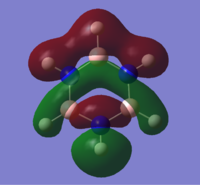
|
| 15 | 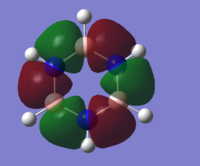
|
| 16 | 
|
| 17 | 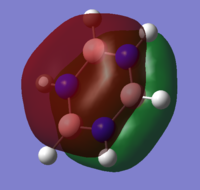
|
| 18 | 
|
| 19 | 
|
| 20 | 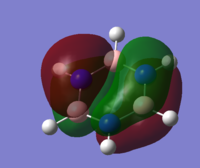
|
| 21 | 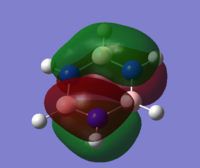
|
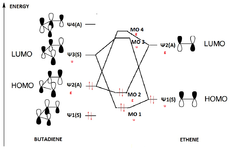
MO diagram of borazine

comparison of the molecular orbitals of benzene, boratabenzene, pyrdine and borazine
| benzene charge | boratabenzene charge | pyridium charge | borazine charge |
|---|---|---|---|
 |
 |
 |
|
 |
 |
 |

|
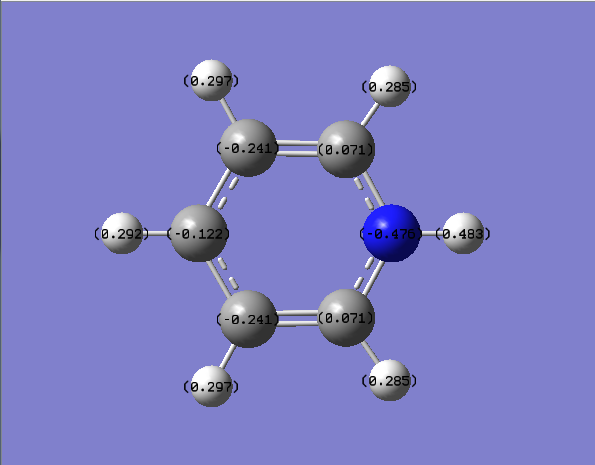
all the four molecules have a delocalised pi bond with a nodal plane through the plane of the molecule. the filled Pz orbital in the boratabenzene molecule allows for a full delcocalised electron ring. in pyrdine the lone pair on the nitrogen isnt participating in the electron overlap.
pyrdinium is the lowest energy orbitsl. this is expected since the nitrogen is much more electronegative comapared to the carbon and boron, and this lowers the energy of all the pyrdinium orbtals. conversly the boratabenzene molecule is the hghest energy due to the boron being highly electropostive. the intermedate energy region for the borazine and benzene is due to benzene being composed solely of carbon and hydrogen, wheras the electrongatvity of the nirogens is offset by the electoposvty of the boron in borazine
pyridium's non contributiing nitrogen orbital therefore has a stabilising affect compared to benzene since it is a antibonding orbital, and since it is playing no part in the bonding this makes it more stable, the boron however contributes to the antibonding significantly so is a higher energy than the benzene.
the molecules HOMO's and HOMO-1 have nodal planes into the ring and a nodal plane perpendicular to the ring. the benzene molecule has a double degenerate HOMO as does the borazine since they both have the same symmetry. since the symmetry changed with boratabenzene and pryidium this becomes no longer true since the boron atom subsitution raises the moecules energy in boratabenzene and the subsiution of nitrogen in pyridum lowers the enrgy.
boratabenzene's HOMO-1 orbital is higher in energy than the HOMO since it has a node in the boron atom and electron density across the boron atom in the HOMO, this makes it destabiised since boron is an electropostive atom. the negative charge assigned to the boratabenzene means that there is a high electron density near the boron atom in the HOMO. the reasoning behind the negative charges on the carbon atoms in the ring are due to borons electron donating ability, meaning the carbons closest to the boron will have a greater electron density giving a asymetric distrubtion of elecron density.
for pyridium the HOMO-1 is lower in enrgy than the HOMO since there is a high amount of electron denisty at the nitrogen atom and the nitrogen is electronegative. the nitrogen will then draw electron density from the carbons closest to it (opposite of the boratabenzene) and this is seen the LCAO
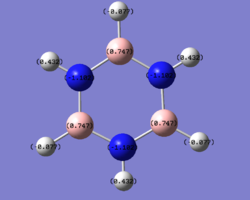
borazines electrongeative nitrogens mean that the orbital with the largest nitrogen contribution will be larger (seen in the HOMO as illistrated) and vice versa with the orbital with 2 boron atoms and 1 nitrogen being smaller.
this is all totally rationalised by comapring the electronegativites of the atoms on the molecule. since the boratabenzene has a electropostive atom it is destabilised and so is higher in energy. the pyridium nitrogen stabilises the molecule since it is electronegatie.