Rep:Mod:syc2013
Bonding and Molecular Orbitals in Main group Chemistry
Shuk Yi Chan
Introduction
Computational chemistry is a division of chemistry which allows chemical problems to be solved through the incorporation of computer science. Through results collected from theoretical chemistry, computational chemistry can be used to simulate chemical processes and investigate chemical properties. It is an important approach t as it could be used to investigate experiments which are too time consuming, costly and unstable to be completed conventionally or to a greater degree of accuracy.
‘Paraphrasing Mike Colvin of Sandia National Laboratory: It is now generally possible to obtain molecular structures (with ~1% accuracy), reaction enthalpies (~1 kcal/mol), dipole moments and infrared intensities, vibrational frequencies (~5%), reaction free energies (~2 kcal/mol), relative acid constants (~2 pKa units), and reaction rates (for certain types of reactions) without doing any laboratory experiments, i.e. at reduced cost. There is also increased safety and faster turnaround when toxic or explosive compounds are involved. There is the prospect of an improved understanding especially when we have both an experimental and theoretical perspective on a problem.’[1]
One popular method for computational chemistry is As Initio, meaning that it comes from first principle. This methods is based upon quantum mechanics (including the Schrödinger equation), with no experimental parameters contributing towards the calculations. Generally, Ab Initio provides a high level of qualitative readings; with very accurate quantitative results for small molecules. Density functional theory (DFT) is a type of Ab Initio calculations which is based upon total electron density (opposed to Wavefunctions (Hartree-Fock), which requires a very high demand in computer power).
Optimization
Through solving the schrödinger equation, the energy of a molecule could be obtained; this energy is dependent upon the position of the nucleus. As a result, a change in nuclei coordinates would lead to the corresponding change in energy. One simple example is the disassociation curve of a diatomic, in which E is dependent upon R. As the nuclei become closer together, they will repel each other and the energy of the system would increase. If the nuclei become further apart, the electrons would no longer form a bond and the electron-nuclear attraction would decrease, the energy would go up and the molecules dissociates. Between the two extremes, the electrons and nuclei are able to rearrange themselves so that the system is in equilibrium, result in there is zero net force acting upon the molecule. Whereas, if the system is not in equilibrium, the mutual interactions are not stable, causing forces to be exerted on the nuclei and electrons forcing them to shift into better conditions. Similarly, in optimization, the most stables point is found through solving the schröndinger equation for the necleaus positions and find the energy, E. through a step-wise process of solving the schrödinger equation each time the atoms are moved apart slightly, until it converges to the most stablest form. (the R point in which the potential energy is the lowest.)Therefore it is the the point when the gradient is zero (or very close to zero) at the first derivatives.
Basis Set
As mentioned previously, the Schrödinger equation needs to be solved in order to obtain the electronic energy of the molecule. In order to solve the Schrödinger equation for more than two particles (a nucleus and electron) approximations are made. Basis sets are used to approximate the wave function, with bigger and more complex basis set providing a closer representation of the wave function. Often, one or more Gaussian function are used to represent each atomic orbital in molecule. Larger and more complex basis functions are formed by increasing the base functions,; the split valence basis set allows for more than one function per valence atomic orbital. 2 basis function per valence atomic orbitals is called a valence double zeta basis set (i.e. 3.21G and 6.3G basis set).
Through the name of the basis set, it is possible to understand the calculation. 3-21G means that each of the core AO (atomic orbitals) in the molecule will be represented by a single contracted Gaussian base function, with a degree of contraction being 3. The two digits after the hyphen implies that it is a valence double-zeta bsis set. The first valence basis function would be a contracted Gaussian basis function, this time with the degree of contraction being 2.The second valence basis function is a primitive Gaussian.
Pseudo Potential
In order to gain a more simplified description of complex molecules, Pseudo-potential can be used as an approximation. In a molecule, there are core electrons which are bounds tightly to the nucleus and valence electrons which are further away. It is proposed that the valence electrons are accountable for most of the properties of the molecule, meaning that the core electrons only have a very small contribution. As a result, in the Pseudo-potential structure only the valence electrons would be considered. The valence electrons are no longer required to be orthogonal to the core state.
Analysis of BH3;BBr3 and TlBr3
BH3
BH3 molecule was optimized at a basis set of 3-21G. Link
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 3.12G |
| Final Energy (au) | -26.46226338 |
| Gradient (au) | 0.00020672 |
| Dipole Moment (Debye) | 0.0000 |
| Point Group | D3h |
| Calculation Time | 70 seconds |
the optimized bond length and bond angle obtained was 1.19349Å and 120o respectively. therefore through considering the level of errors in the system, the final bond length is 1.19Å and 120o bond angle.
<pre|right>
Item Value Threshold Converged?
Maximum Force 0.000413 0.000450 YES
RMS Force 0.000271 0.000300 YES
Maximum Displacement 0.001610 0.001800 YES
RMS Displacement 0.001054 0.001200 YES
Predicted change in Energy=-1.071764D-06
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1935 -DE/DX = 0.0004 !
! R2 R(1,3) 1.1935 -DE/DX = 0.0004 !
! R3 R(1,4) 1.1935 -DE/DX = 0.0004 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
BH3 molecule was optimized at a basis set of 6-31G(d,p) by using a better basis set; a more accurate bond length could be obtained. Link
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy (au) | -26.61532363 |
| Gradient (au) | 0.00000235 |
| Dipole Moment (Debye) | 0.0000 |
| Point Group | D3h |
| Calculation Time | 39 seconds |
Item Value Threshold Converged?
Maximum Force 0.000005 0.000450 YES
RMS Force 0.000003 0.000300 YES
Maximum Displacement 0.000019 0.001800 YES
RMS Displacement 0.000012 0.001200 YES
Predicted change in Energy=-1.304899D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1923 -DE/DX = 0.0 !
! R2 R(1,3) 1.1923 -DE/DX = 0.0 !
! R3 R(1,4) 1.1923 -DE/DX = 0.0 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
the calculated bond length was 1.9232Å, with a bond length of 120o; which leads to a final answer of 1.92Å and 120o.
There is a 0.00206Å difference between the basis set 3.21G and 6.31G(d,p). the bond length of 1.9232Å is expected to be a closer representation of the true value, as p-type functions has been added to the H atom and d-type function to the atoms with Z>2. The addition of polarization lead to additional flexibility to the basis set, allowing the hydrogen molecular orbitals to become more asymmetric. This provides a more accurate representation of bending between atoms as the bond atoms are able to influence the energetic environment of the electrons.
furthermore, different energy were reported for the basis sets, with -26.4622au(±0.00381au) for 3.21G and -26.6153au(±0.00381au) for 6.31G(d,p).
TlBr3
TlBr3 molecule was optimized at a LanL2DZ basis set Link [1]
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | LANL2DZ |
| Final Energy (au) | -91.21812851 |
| Gradient (au) | 0.00000235 |
| Dipole Moment (Debye) | 0.00000090 |
| Point Group | D3h |
| Calculation Time | 24.7 seconds |
Item Value Threshold Converged?
Maximum Force 0.000002 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000022 0.001800 YES
RMS Displacement 0.000014 0.001200 YES
Predicted change in Energy=-6.084017D-11
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 2.651 -DE/DX = 0.0 !
! R2 R(1,3) 2.651 -DE/DX = 0.0 !
! R3 R(1,4) 2.651 -DE/DX = 0.0 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
The optimised bond length calculated is 2.65095Å with a bond angle of 120o; resulting in a final bond length of 2.65Å. The dipole moment will be considered to be 0.00Debye.
X-ray diffraction of TlBr3 found the Tl-Br bond length to be 2.5122Å[2]; as a result the calculated results has overestimated the bond length. As mentioned previously, DFT could only provide qualitative data for large molecules; therefore a very accurate result should not have been expected. Furthermore, in the experimental bond length, it was predicted that two water molecules are bonded tightly to the TlBr3, leading to a trigonal-bipyramidal. This would lead to a change in bond length and orientation, which was not considered in the Gaussian calculation
BBr3
BBr3 molecule was optimized at a basis set of GEN. Link DOI:10042/22703
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | GEN |
| Final Energy (au) | -64.43645296 |
| Gradient (au) | 0.00000382 |
| Dipole Moment (Debye) | 0.00000090 |
| Point Group | D3h |
| Calculation Time | 39.2 seconds |
Item Value Threshold Converged?
Maximum Force 0.000008 0.000450 YES
RMS Force 0.000005 0.000300 YES
Maximum Displacement 0.000036 0.001800 YES
RMS Displacement 0.000023 0.001200 YES
Predicted change in Energy=-4.026779D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.934 -DE/DX = 0.0 !
! R2 R(1,3) 1.934 -DE/DX = 0.0 !
! R3 R(1,4) 1.934 -DE/DX = 0.0 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
The optimised bond length calculated is 1.93396Å with a bond angle of 120o; after considering the error involved in the calculation the final bond length is 1.93Å. the dipole moment would be considered to be 0.00Debye.
Analysis
| Molecule | Bond Length (Å) |
|---|---|
| BH3 | 1.92 |
| TlBr3 | 2.65 |
| BBr3 | 1.93 |
All three molecules has a trigonal planar structure with a bond angle of 120o; BH3 has the shortest bond length and TlBr3 has the longest. Long bonds generally weaker in strength than shorter ones and therefore less energy is required to break the bond apart. Bond length is effected by atomic size, electronegativity and orbital overlap.
The change in bond length between BH3 and BBr3 suggest that the change in ligands has had an effect on the structure. Two ligands has been used within the calculations; hydrogen and bromine atom, with the main difference between the two being atomic size. Firstly, bond length is the distance between the centres for two covalently bonded atoms, with the length being approximately the sum of the covalent radii of the two atoms. (Both H and Br bond form covalent bonds with the B atom.) When comparing the difference in bond length in BH3 and BBr3; Br has a larger atomic radii compared to the hydrogen atom leading to a larger B-Br bond length. Both H and Br are similar because they both require one more electron in order to form a full outer shell, which were achieved by covalently bonding with the B centre. Theese valence electrons are on different shells (H atom: 1S1 compared to 4p5); with the boron atom (2p1 valence shell) forming a better overlap with the hydrogen 1S orbital due to smaller size. Whereas, the bromine atom’s orbital significantly larger and more diffuse than the boron atom leading to a poorer overlap.
The change in central atom had also led to a change in bond length, with the Tl atom being significantly larger than the B atom. A similarity between the two atoms is that they are both in group 13 of the periodic table, therefore their valence shells are ns2, np1. Similarly to the above explanation, the increase in atomic size leads to a greater bond length. Furthermore, for the TlBr3, there is a greater mismatch between orbital size between the Tl and Br atoms, leading to a lower degree of overlap and weaker bond. Whereas boron orbitals are much less diffuse as they are closer to the nucleus resulting in a stronger overlap between the orbitals. Generally, atomic orbitals which would lead to the greatest stabilisation energy are those with similar energies and to some extent electronegativity. The electronegativity of the B, Br and Tl atoms are 2.04, 2.96 and 1.62; with a smaller difference in electronegativity between B-Br than Tl-Br bond.
Gaussview
Pictorially a chemical bond is shown by a line which is drawn between two bonds; in Gaussview, a bond is formed when the inter-nuclear distance between the two atoms are in sufficient proximity in an area of high electron density. If this distance is beyond the Gaussian’s internal list of bond lengths, Gaussview would fail to recognise that a bond is present and therefore fails to draw a bond. Gaussview are able to recognise most bonds in organic molecules as they are generally relatively short in length; however it would frequently struggle with inorganic molecules with typically longer bond lengths.
A simplified view of a bond is an attraction between atoms which leads to the formation of chemical molecules with multiple atoms and bonds. This bond is caused by the electrostatic force between the opposite charges, for example, between the electrons and nuclei. With it leading to a region of high electron density between two bonds and a lowering in energy (than if the two atoms were not interacting).
Frequency Analysis
In order to verify whether the obtained configuration obtained by the optimization calculation is correct; frequency is used to verify that it is the minimum energy point through secondary derivative. Within the vibration analysis, there is a 10% error present within the calculation.
BH3 Analysis
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6.31G (d,p) |
| Final Energy (au) | -26.615322363 |
| Gradient (au) | 0.00000237 |
| Dipole Moment (Debye) | 0.0000 |
| Point Group | D3h |
| Calculation Time | 23 seconds |
Low frequencies --- -0.9033 -0.7343 -0.0054 6.7375 12.2491 12.2824 Low frequencies --- 1163.0003 1213.1853 1213.1880
The frequencies are centred around zero and have a range within 15cm-1; confirming that the lowest energy configuration had been obtained.
| no. | Form of Vibrations | Frequency(cm-1) | Intensity | Symmetry(D3h) | Symmetry (D3h) |
|---|---|---|---|---|---|
| 1 |
|
1163.00 | 92.5478 | A2" | Out-of-plane wagging. The hydrogen atoms are moving above and below the boron atom in an ‘umbrella-opening’ motion; with the boron atom being displaced from its equilibrium position by each movement. |
| 2 |  |
1213.19 | 14.0553 | E' | Symmetric wagging. Two of the B-H bonds are scissoring, with the bond length remain unchanged through the motion. |
| 3 |  |
1213.19 | 14.0589 | E' | Two bonds are rocking in the same direction, with their bond length unchanged. Whereas,the last bond is wagging, with the bond length changing continuously. |
| 4 |  |
2582.26 | 0.0000 | A1' | Symmetric stretch. All through of the B-H bonds are simultaneously stretching and compressing. The dipole moment of the molecule does not changed, resulting in this vibration being IR inactive. |
| 5 |  |
2715.43 | 126.3307 | E' | Asymmetric stretch. Two bonds are stretching asymmetrically with respect to one another; whilst the last bond remain stationary. |
| 6 | |
2715.43 | 126.3211 | E' | Two of the B-H bonds are rocking in the same direction with respect to each other. Whilst the last bond is wagging, whilst being stretched and compressed. |
The infrared Spectrum of BH3h):
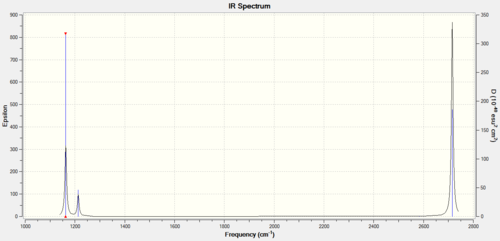
The literature values for the molecule are (cm-1 1225, 1305 and 2693. (value of 2813 was calculated but not observed in literature.)[3] Which corresponds relatively well with the calculated data.
Although 6 vibrations were calculated; only three peaks are present in the IR spectrum. the two pairs of vibrations with the symmetry label of E’ are degenerate, and would never for result in overall 2 bonds instead of the maximum number of 4. A2’’ would be the third peak to be present in the spectrum. The stretch with the symmetry of A1’ would not produce a peak as there was not a change in dipole moment.
TlBr3 Analysis
To ensure that the proposed structure of TlBr3 is correct; frequency analysis is performed upon the optimized structure. Link DOI:10042/22614
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | LANL2DZ |
| Final Energy (au) | -91.21812851 |
| Gradient (au) | 0.00000088 |
| Dipole Moment (Debye) | 0.0000 |
| Point Group | D3h |
| Calculation Time | 30.5 |
Low frequencies --- -3.4213 -0.0026 -0.0004 0.0015 3.9367 3.9367
Low frequencies --- 46.4289 46.4292 52.1449
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
E' E' A2"
Frequencies -- 46.4289 46.4292 52.1449
Red. masses -- 88.4613 88.4613 117.7209
Frc consts -- 0.1124 0.1124 0.1886
IR Inten -- 3.6867 3.6867 5.8466
Atom AN X Y Z X Y Z X Y Z
1 81 0.00 0.28 0.00 -0.28 0.00 0.00 0.00 0.00 0.55
2 35 0.00 0.26 0.00 0.74 0.00 0.00 0.00 0.00 -0.48
3 35 0.43 -0.49 0.00 -0.01 -0.43 0.00 0.00 0.00 -0.48
4 35 -0.43 -0.49 0.00 -0.01 0.43 0.00 0.00 0.00 -0.48
4 5 6
A1' E' E'
Frequencies -- 165.2685 210.6948 210.6948
Red. masses -- 78.9183 101.4032 101.4032
Frc consts -- 1.2700 2.6522 2.6522
IR Inten -- 0.0000 25.4830 25.4797
Atom AN X Y Z X Y Z X Y Z
1 81 0.00 0.00 0.00 0.42 0.00 0.00 0.00 0.42 0.00
2 35 0.00 -0.58 0.00 0.01 0.00 0.00 0.00 -0.74 0.00
3 35 0.50 0.29 0.00 -0.55 -0.32 0.00 -0.32 -0.18 0.00
4 35 -0.50 0.29 0.00 -0.55 0.32 0.00 0.32 -0.18 0.00
| no. | Form of Vibrations | Frequency | Intensity | Symmetry (D3h) | Description |
|---|---|---|---|---|---|
| 1 |  |
46.43 | 3.6867 | E' | Scissoring. Two Tl-Br bonds are scissoring without a change in bond length. |
| 2 |  |
46.43 | 3.6867 | E' | Two of the Tl-Br bonds are rocking up and down without a change in bond length. The last bond is stretching and compressing whilst it is wagging in a horizontal direction |
| 3 |  |
52.14 | 5.8466 | A2" | Out-of-plane wagging. The bromine atoms are moving in an ‘umbrella-opening’ motion above and below the thallium atom. The Tl-Br bonds length remain constant in the vibration |
| 4 |  |
165.27 | 0.0000 | A1' | Symmetric stretch. The Tl-Br bonds are compressing and stretching simultaneously, leading to an IR inactive stretch as there are no change in dipole moment. |
| 5 |  |
210.69 | 25.4830 | E' | Asymmetric stretch. One bromine atom remain stationary, whilst the other two bonds are asymmetrically stretching and compressing with respect to one another. |
| 6 |  |
210.69 | 25.4797 | E' | Asymmetric stretch. Two of the Tl-Br bonds would stretch symmetrically; whilst the last bond would be compressing. And vice versa. |
the infrared Spectrum of TlBr3
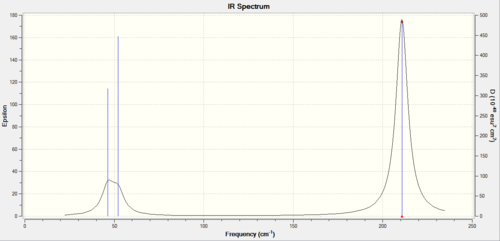
In the infrared, three peaks are present. Similarly to BH3; a pair of E' are degenerate and would only give a single peak.
comparisons
| BBr3 | TlBr3 | |||||
|---|---|---|---|---|---|---|
| Freq(cm-1) | Intensity | symmetry | Freq(cm-1) | Intensity | symmetry | |
| 1163.00 | 92.5478 | A2" | 46.43 | 3.6867 | E' | |
| 1213.19 | 14.0553 | E' | 46.43 | 3.6867 | E' | |
| 1213.19 | 14.0553 | E' | 46.43 | 3.6867 | E' | |
| 2582.26 | 14.0589 | E' | 52.14 | 5.8466 | A2" | |
| 2582.26 | 0.0000 | A1' | 165.27 | 0.0000 | A1' | |
| 2715.43 | 126.3307 | E' | 210.69 | 25.4830 | E' | |
| 2715.43 | 126.3211 | E' | 210.69 | 25.4797 | E' |
There is a large difference in frequency, with the BBr3 being significantly higher than those of TlBr3. This is due to the large difference in mass between the sentral atom, with thallium being significantly larger and heavier. The vibrational frequency of the a molecule could be defined as
v = (1/2πC)(k/µ)0.5
With C being the speed of light, µ is the reduced mass and k is the spring constant (linked to bond strength). The equation shows that the frequency is inversely proportional to the square root of the reduced mass of the system; therefore an increased mass would lead to a decrease in the frequency. TlBr3 has a greater reduced mass compared to BBr3; therefore TlBr3 would have lower vibrational frequency values. With the large difference in frequency values between the two molecules being due to their big difference in size and mass.
A reordering of modes has occurred between BBr3 and TlBr3, although the same number of modes are present in both systems. A2’’ mode is the lowest mode in BBr3; whereas it is the E’ mode for the TlBr3 molecule. As a result, the spectra are relatively similar, with three peaks present in each spectrum; in a relatively similar pattern. (With 2 peaks positioned at a low frequency and a single strong peak at a significantly higher frequency.) The low frequency at BBr3 exhibit to clear peaks, whereas TlBr3’s peaks has overlapped. For both spectra, the vibrational mode A2’’ and E’ lie very closely together but at a higher energy; this is because these modes are bending motion of similar energy (the higher frequency peak is high energy stretching modes).
Frequency Calculations
It is important that the same method and basis set are used for both optimisation and the frequency analysis, as it would lead to possibly less accurate results with a higher degree of errors. Complex basis sets are able to provide a relatively accurate representation of the atomic orbitals; therefore if a simpler basis set is used after. The degree of errors would have increased in magnitude. As a result, the same method and basis set should be used for optimisation, frequency and any other subsequent calculations.
A frequency calculation is very important as it ensures that the optimization was completed successfully. In the optimisation, the lowest energy molecule is calculated through convergence to a structure in which the first derivative is zero (zero gradients). This could either be the desired lowest energy conformation or the transition state; therefore through the second derivatives, it is possible to accurately distinguish between the two. The frequency analysis calculates the second derivative; if the second derivatives are positive this means that the minimum energy conformation has been obtained. Whereas, negative values would suggest that the transition state has been obtained.
Low frequency are found in the .log files of the frequency analysis, these provide information about the degree of convergence of the obtained optimised molecular structure. These frequencies for rotation and translational modes should be as close to zero as possible. Therefore, if a transition state or higher order saddle point has been obtained; negative frequencies would be listed before the ‘zero frequency’ modes. Frequencies for rotations are often relatively large, for DFT calculations, the frequencies are normally less than a few tens of wavenumbers (such as 50).
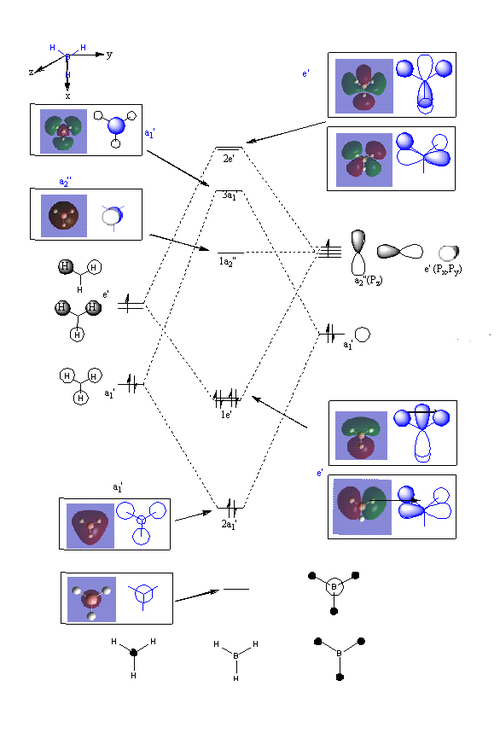
Molecular Orbitals of BH3
Through the Gaussian software, the molecular orbitals of the molecule could be obtained. link DOI:10042/22704
| File Type | .log |
| Calculation Type | SP |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G (d,p) |
| Final Energy (au) | -26.61532363 |
| Dipole Moment (Debye) | 0.0000 |
| Point Group | D3h |
| Calculation Time | 13.5 seconds |
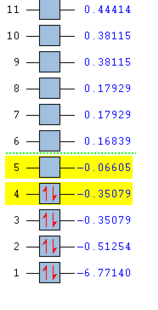
| HOMO-3 | HOMO-2 | HOMO-1 | HOMO |
|---|---|---|---|
 |
 |
 |
|
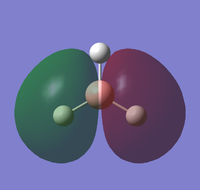| LUMO | LUMO+1 | LUMO+2 | LUMO+3 |
 |
 |
 |
|
The molecular orbitals can be compared with those predicted by Molecule Orbital theory and LCAO.
Alpha MO
Generally, the calculated molecular orbitals corresponded well to those predicted through the MO diagram. There does not appear to be any significant difference between the two, supporting the MO theory. This suggests that the basis of Mo theory is correct and that it is possible to predict the molecular orbitals through the linear combination of the atomic orbitals.
The difference between real and LCAO molecular orbital is the LCAO generally only consider the valence electrons. Whilst, the real MO would also consider 1s1 atomic molecule, and how they interact with the hydrogen atomic orbitals; which leads to an additional MO in the computed calculations. As a result, the real molecule considers all 8 electrons, whilst LCAO only focus on 6 electrons.
Analysis of NH3
Optimization
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy (au) | -56.55776873 |
| Gradient (au) | 0.00000323 |
| Dipole Moment (Debye) | 1.8465 |
| Point Group | C3v |
| Calculation Time | 43 seconds |
Item Value Threshold Converged?
Maximum Force 0.000006 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000012 0.001800 YES
RMS Displacement 0.000008 0.001200 YES
Predicted change in Energy=-9.844576D-11
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7446 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7446 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7446 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8637 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
the optimised bond length calculated is 1.01798Å with a bond angle of 37.128o; leading to a final answer of 1.02Å and 37.1o. With a dipole moment of 1.8 Debye.
Frequency
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy (au) | -56.55776873 |
| Gradient (au) | 0.00000332 |
| Dipole Moment (Debye) | 1.8465 |
| Point Group | C3 |
| Calculation Time | 26.0 seconds |
Low frequencies --- -0.0130 -0.0013 0.0017 7.0759 8.0928 8.0931 Low frequencies --- 1089.3840 1693.9368 1693.9368
The frequencies are within the range of 15cm-1; suggesting that the optimised molecule is the molecule at its most stablest form.
Molecular Orbitals
| File Type | .chk |
| Calculation Type | SP |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy (au) | -56.55776873 |
| Gradient (au) | 0.00000332 |
| Dipole Moment (Debye) | 1.8465 |
| Point Group | C3v |
| Calculation Time | 10 seconds |
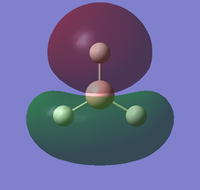
the molecular orbitals of the NH3 molecule was obtained. The first 8 are:
| HOMO-4 | HOMO-3 | HOMO-2 | HOMO-1 |
|---|---|---|---|
 |
 |
 |
|
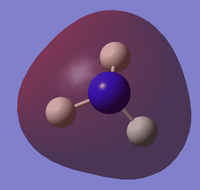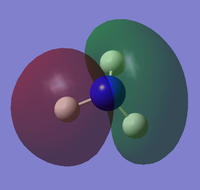| HOMO | LUMO | LUMO+1 | LUMO+2 |
 |
 |
 |
|
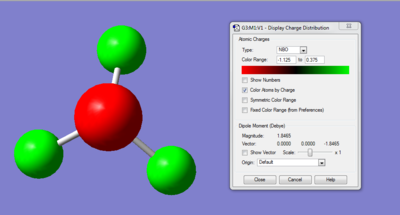
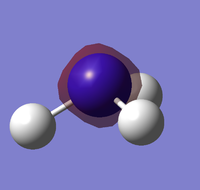
NBO analysis on NH3
The charge distribution of the molecule can be shown through Natural Bond Orbital Analysis. Bright green indicates highly positive charge and bright red highly negative charge. With the charge range being from -1.125 (red) to 0.375 (green).
This indicates that the hydrogen atoms has relatively high positive charge and the negative has a high negative charge. This corresponds well to electronegativity difference between the two atoms. Compared to hydrogen, the nitrogen atom is very electronegative and would therefore pull electron density away from the hydrogen, resulting in a polar molecule.
By viewing the charge by number, it is clear that the nitrogen atom is withdrawing electron density equally from all three hydrogen. As the three positive charges on the hydrogen cancels out the negative charge on nitrogen. Resulting in an overall neutral molecule.
Association energies: Ammonia-Borane
Optimization
the molecule is optimised with a basis set of 6.31G(d,p) in order to obtain the most stablest form. link
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6.31G(d,p) |
| Final Energy (au) | -83.22468893 |
| Gradient (au) | 0.00005976 |
| Dipole Moment (Debye) | 5.5651 |
| Point Group | C1 |
| Calculation Time | 7 minutes 7.0 seconds |
Item Value Threshold Converged?
Maximum Force 0.000122 0.000450 YES
RMS Force 0.000058 0.000300 YES
Maximum Displacement 0.000513 0.001800 YES
RMS Displacement 0.000296 0.001200 YES
Predicted change in Energy=-1.631256D-07
Optimization completed.
-- Stationary point found.
the obtained bond length for the N-H, N-B and B-H bonds are 1.01861Å, 1.66803Å and 1.21008Å respectively. After considering the errors, the obtained bond lengths are 1.02Å, 1.67Å and 1.21Å respectively. the molecule would have a calculated dipole moment of 5.57Debye.
Frequency
To ensure that the optimised molecule is correct; the frequency of the molecule is obtained. Link
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6.31G(d,p) |
| Final Energy (au) | -83.22468909 |
| Gradient (au) | 0.00000108 |
| Dipole Moment (debye) | 5.5646 |
| Point Group | C1 |
| Calculation Time | 2 minute 24.0 seconds |
Low frequencies --- -3.2361 -0.0010 0.0002 0.0006 1.4238 4.4117 Low frequencies --- 263.4409 632.9551 638.4299
Energy Comparisons
E(NH3)=--26.61532363au
E(BH3)=-56.55776873au
E(NH3BH3)=-83.22468893au
ΔE=E(NH3BH3)-[E(NH3)+E(BH3)]
ΔE=(-83.22468893)-[-56.55776873+-26.46226338]
ΔE= -0.05159657
1a.u. = 2625.50KJ mol-1
Therefore: ΔE= -135.4667945KJmol-1 (±10Kj mol-1)
This is the association (and dissociation energy) for combining a molecule of NH3 and a molecule of BH3 together. There is an error of ±10Kj mol-1 for this calculation, which is equivalent to 0.00381au.
A literature value for this association energy is 27.6Kcal mol-1)[4] which is equivalent to 115.48Kj mol-1). As this is calculated using a different method and basis set, only a very qualitative comparison can be made between the two results. The association energy are relatively similar in value, indicating that the calculation was done relatively accurately.
Conclusion
Through this investigation, it is understand that through computational chemistry it is possible to acuurately calculate the bond length, vibrations, energy and molecule orbitals of a simple molecule.
Reference
- ↑ www.wellesley.edu/.../Lab07/07Chem105LComputationPrelab.doc
- ↑ Glase, J. Johansson; On the Structure of the Hydrated Thallium (lll) Ion and its Bromide Complexes in Aqueous Solution. Acta Chemica Scandinavica (1982) 125-135
- ↑ Kawaguchi, K; Butler, J.E.; Yamada, C.; Bauer, S.H; Minowa, T. Observation of the gasphase infrared spectrum of BH3. J. Chem. Phys. 87, 2438 (1987); doi: 10.1063/1.453135
- ↑ Zirz, C; Ahlrichs, R. Theoretical computation of the binding energy of BH3NH3, a difficult case. : J. Chem. Phys. 75, 4980 (1981); doi: 10.1063/1.441886