Rep:Mod:swphys3

Module 3 - Transition states and reactivity

Scot Wheeler

Year 3 computational lab module 3

The Cope Rearrangement

The Cope rearrangement, a [3,3]-sigmatropic shift rearrangement, of 1,5-hexadiene is generally accepted to occur via a concerted mechanism via either a chair or boat transition structure. The Cope rearrangement is shown below with the two possible transition structures.

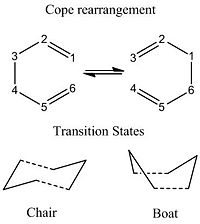
Using computational methods it's possible to model the reactants, products and transition state structures to locate the low energy minima and transition states on the potential energy surface, using this information to determine the mechanism.

Optimisation of 1,5-hexadiene

Firstly 1,5-hexadiene was drawn in GaussView with an anti linkage for the central 4 atoms. The structure was optimised at the HF/3-21G level and the final energy and symmetry noted. It was noticed that there are numerous conformations of the anti as well as with the central 4 atoms in a gauche conformation. A couple of each were also modelled with the results and structures recorded in the table below.

Reactant optimisation

				Gauche 3
Energy (a.u.)	-231.6926	-231.6925	-231.6917	-231.6925
Point Group	C2	Ci	C2	C1

Generally it is expected that the anti conformers have a lower energy because the carbon atoms are kept as far away from each other as possible, resulting in the least steric hindrance; this is seen above as the anti conformers have a more negative energy. However the conformer which is found to have the lowest energy is a gauche conformer (gauche 3 in reference table) with energy -231.69266 a.u. and C₁ symmetry. This is thought to be because of favourable Van der Waals interactions between Hydrogen atoms at certain distances, also C-H σ* - C-C π overlap is also possible. The conformers found above have been labelled in comparison to this in the reference table.

The anti 2 conformation was modelled and optimised at the HF/3-21G level, then reoptimised at the higher B3LYP/6-31G(d) level and the structures have been compared in the table below. The final energy was reported as -234.6117 a.u. but it's not possible to compare energies as the method has changed.

Comparison of angles and bond lengths in optimised structures of the anti2 conformer

Property	1st Opt (HF/3-21G)	2nd Opt (B3LYP/6-31G*)
Dihedral Angle (o): C1-C2-C3-C4	114.7	118.6
Bond Angle (o): C1-C2-C3	124.8	125.3
Bond Angle (o): C2-C3-C4	111.3	112.7
Bond length (Å): C1=C2	1.32	1.33
Bond Length (Å): C2-C3	1.51	1.50
Bond Length (Å): C3-C4	1.55	1.55

The structure remains very similar between the two optimisation methods. Bond lengths are almost identical and compare well to 1.34 Å and 1.54 Å expected for C=C and C-C bonds respectively. The largest difference is with some of the angles, generally showing a slight increase in angle for second method.

Frequency calculation

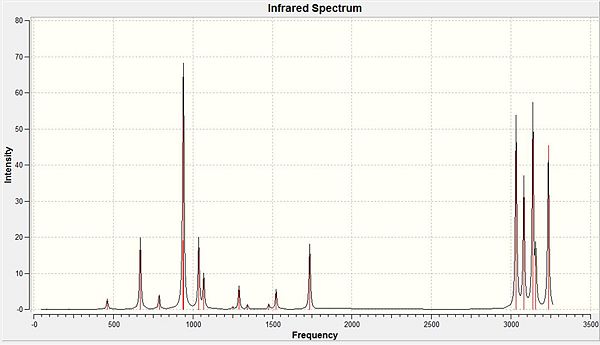
To confirm the geometry minimum is in fact a minimum a frequency calculation was carried out and the output checked to ensure all frequencies were positive. This was the case and some of the frequencies as well as the IR spectrum are located in the table below. DOI:10042/to-7194

Vibrations of the anti2 conformer

Frequency (cm-1)	Animated Vibration	Description	Intensity
1734		C=C stretch	18.13
3032		alkane C-H stretch	53.60
3081		alkane C-H stretch	35.91
3137		C-H stretch	56.01
3156		alkene C-H stretch	14.70
3234		alkene C-H stretch	45.48

There is an error associated with these calculated frequencies due to the harmonic potential approximation used instead of an anharmonic potential. This tends to lead to frequency values higher than that seen experimentally, with an error up to 10%. To improve these frequencies a higher basis set would be required.

From the output file, under the heading thermochemistry there are numerous vibrational temperatures which are recorded in the table below.

Energy	Value (a. u.)
Sum of electronic and zero-point Energies	-234.469183
Sum of electronic and thermal Energies	-234.461843
Sum of electronic and thermal Enthalpies	-234.460898
Sum of electronic and thermal Free Energies	-234.500743

The 'sum of electronic and zero-point energies' is the potential energy at 0 K including the zero-point energy (E = E_elec + ZPE).

The 'sum of electronic and thermal energies' is the energy at 298 K and 1 atm including translational, rotational and vibrational energy modes (E = E + E_vib + E_rot + E_trans).

The 'sum of electronic and thermal enthalpies' contains a correction for RT (H = E + RT).

The 'sum of electronic and thermal free energies' includes the entropic contribution to free energy (G = H - TS).

Optimising the 'Chair' and 'Boat' transition structures

Following the optimisation of the reactants, next the transition states were optimised. There are two possible transition state geometries, chair and boat. Firstly a CH₂CHCH₂ fragment was drawn in GaussView and optimised at the HF/3-21G level. This was then copied and pasted twice into a new window and arranged into a chair conformation with the terminal carbon atoms ~2.2 Å apart. This was then optimised in two different ways: The first was to calculate the force constant matrix (the Hessian) as the first step, which was then recalculated throughout the optimisation. The initial guess has to be accurate to that of the transition state as the method is very sensitive to the input geometry. The second method involves freezing the reaction coordinate and minimising the rest of the molecule. The molecule is then unfrozen and the transition state is optimised again. The advantage is that it's not necessary to calculate the whole Hessian.

TS(Berny) method

An opt+freq calculation was set up, with 'Optimise to a TS (Berny)' and 'calculate force constants once' selected. The additional keywords 'Opt=NoEigen' were added to stop the calculation crashing if more than one imaginary frequency is detected. The calculation completed and one imaginary frequency was found with the expected magnitude of 818 cm^-1. This vibration corresponds to the connection/disconnection of appropriate bonds in the cope rearrangement and can been seen below. TS(Berny) log file

Frozen coordinate method

The second method used the 'redundant coordinate editor' to restrict the distance between the terminal carbons to 2.2 Å, the rest of the molecule was optimised. The second step was to 'unfreeze' this distance, and the molecule optimised again. It resulted in the same outcome as the previous method, with an imaginary frequency found at 818 cm^-1. The final distance between the terminal carbons of the two segments for method 1 and method 2 were 2.0206 Å and 2.0205 Å indicating both methods are consistent but this is because the initial guess was close to that of the actual transition state. Both methods have their limitations, the first one requires the input to be very similar to that of the transition structure in question; while the second method requires a close estimation of the terminal distance.

Optimisation of boat transition state

A different method (QST2) was used for the boat transition structure; for the QST2 method the reactants and products are specified for a reaction and the calculation will attempt to find the transition state. The optimised anti 1,5 hexadiene molecule from earlier was introduced twice into GaussView as part of a 'MolGroup'. The product structure atom labels were edited to ensure they match the reactant. The molecules need to be drawn so that they are close to the transition state, this was seen when the calculation was attempted and failed while the structures were that of the anti conformer. The geometries were altered so the central 4 carbon atoms had dihedral angle of 0^o and the inside C-C-C angle was 100^o.

The resulting structure from the QTS2 method had an energy of -231.603 a.u. There was one imaginary frequency, indicating the successful location of a transition state. The vibration had a frequency of -840 cm^-1. Boat TS QST2 optimisation log file

Intrinsic Reaction Coordinate Method

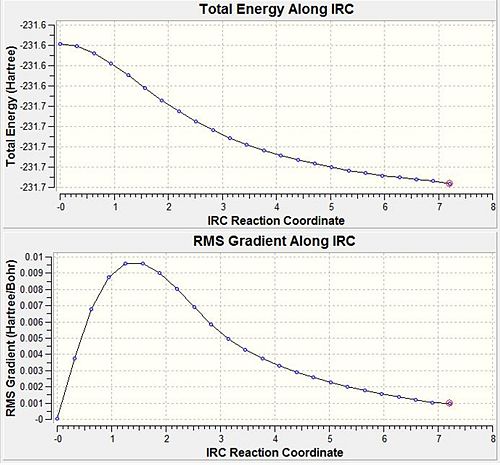
A method in Gaussian makes it possible to follow the minimum energy pathway from a transition structure down to the local minimum on a potential energy surface. A series of points are obtained by taking small changes in geometries in the direction where the gradient of the energy surface is steepest. From this analysis it is possible to determine which 1,5-hexadiene conformer the TS is associated with. The HF/3-21G optimised chair transition state found earlier was used, with 50 points on the IRC pathway with the force constant computed at the start. The resulting geometry after 25 points is shown below with an energy of -231.688 a.u. however it has not reached a minimum, although is similar in structure to the gauche2 conformer. DOI:10042/to-7196

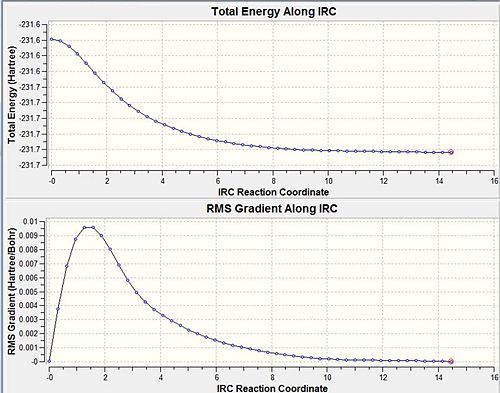
In an attempt to find a better minimum, the calculation was re-run, but the method was changed so that the force constant was calculated at every step. This is more reliable and allows the calculation to ensure it's travelling down the minimum energy pathway. It can be seen from the graphs below that a definite minimum has been located after 47 steps and has a final energy of -231.692 a.u. corresponding to the gauche2 conformer.DOI:10042/to-7197

Activation energies for transition state

To calculate the activation energies the transition structures need to be optimised using the B3LYP/6-31G(d) level of theory, the HF/3-21G optimised structures were used as the starting structures. The energies of the two transition state structures are listed in the table below, with the energies at 0 K and 298 K found from the Thermochemistry section of the log file.

Chair TS activation energy DOI:10042/to-7198

Boat TS activation energy DOI:10042/to-7199

Summery of energies (in Hartree)

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.619	-231.467	-231.461	-234.557	-234.415	-234.409
Boat TS	-231.603	-231.451	-231.445	-234.543	-234.402	-234.396
Reactant (anti2)	-231.693	-231.540	-231.533	-234.612	-234.469	-234.462

We can see there is a difference in energy between the two methods, but this is due to the fact that different methods have been used and it's not possible to compare these energies. We can now calculate the activation energy for the two transition structures by comparing the energies in the table above with the energies calculated for the optimised reactant.

Summary of activation energies (in kcal/mol)

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.81	45.18	33.89	33.26	33.5 ± 0.5
ΔE (Boat)	55.85	55.22	42.04	41.42	44.7 ± 2.0

From the data above we can see that the activation energies determined by the B3LYP level of theory are in very close agreement with the reported experimental values. Those predicted from the first HF/3-21G optimisation are not as comparable with experiment as this is a lower level calculation. We can also confirm that the chair transition state has a lower activation energy compared to the boat transition state which could be due to less steric hindrance in the chair TS. As we have calculated the chair transition state to have the lower activation we would expect this to be the transition state expected for the Cope rearrangement of 1,5-hexadiene.

Diels Alder Cycloaddition

The Diels-Alder is a [4π + 2π] pericyclic cycloaddition reaction between a conjugated diene and an alkene (referred to as the dienophile). The HOMO/LUMO of one reacts with the HOMO/LUMO of the other to form two new bonding/antibonding MOs via a single transition state which is partially stabilised by it's aromatic character. The most simple Diels-Alder reaction is between that of ethylene and cis-butadiene which is investigated first. Later the regioselectivity of the Diels-Alder reaction is studied with cyclohexa-1,3-diene and maleic anhydride.

cis-Butadiene and Ethylene

Cis-Butadiene and Ethylene react together in a Diels-Alder reaction shown below.

Reactants

Firstly the two reactants, cis-butadiene and ethylene, were optimised using the semi-empirical AM1 method, and the HOMO and LUMO generated for each.

Reactant	Molecular Orbital		Symmetry
cis-Butadiene	LUMO		Symmetric
	HOMO		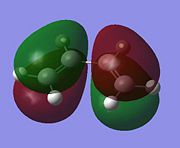Anti-symmetric
Ethylene	LUMO		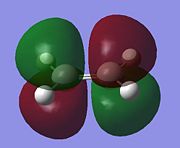Anti-symmetric
	HOMO		Symmetric

The LUMO of butadiene and the HOMO of ethylene are both symmetric with respect to the reflection plane, while the HOMO of butadiene and the LUMO of ethylene are anti-symmetric. As orbital symmetry is very important in Diels-Alder, determining whether a reaction will occur or not, and the stereo outcome of the reaction. The HOMO of ethylene will react with the LUMO of butadiene and the HOMO of butadiene will react with the LUMO of ethylene .

cis-butadiene DOI:10042/to-7179

ethylene DOI:10042/to-7180

Transition State

To calculate the transition state, the 'frozen coordinate method' was used as described above. Firstly the optimised reactants were arranged into a similar geometry to that predicted, an envelope type structure which maximises orbital overlap. Then it was optimised using the semi-empirical AM1 method with the forming C-C bond frozen at 2.2 . The result was then optimised to a TS(Berny) and a frequency analysis completed using the semi-empirical AM1 method with the C-C bond distances unfrozen. One imaginary frequency was found indicating the successful location of a transition state. Finally a higher level DFT/B3LYP/6-31G(d)opt+freq calculation was completed. When a frequency calculation was run, the additional keywords opt=NoEigen were included.

Properties	semi-empirical/AM1	DFT/B3LYP/6-31G(d)
Energy (a.u.)	0.112	-234.544
Imaginary Frequency (cm-1)	-957	-525
Vibration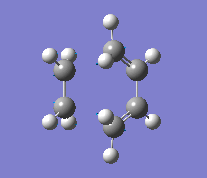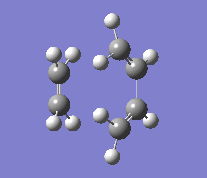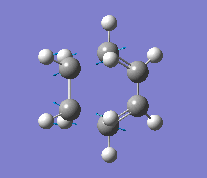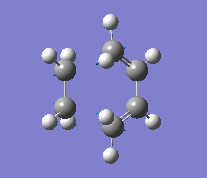
C-C Bond Forming Length (Å)	2.12	2.27

Although it's not possible to compare the energy of the two methods, the C-C forming bond lengths do differ. The more accurate B3LYP method reports a bond length 0.15 Å longer than that of the AM1 method. The frequencies reported also appear very different in value, but this is only due to the method used. As they are imaginary frequencies, their actual value is irrelevant. More importantly is the vibration seen, it shows that the bond forming is synchronous, evidence that the reaction does occur with a concerted mechanism.

TS (semi-empirical AM1) DOI:10042/to-7181

TS (DFT/B3LYP/6-31G(d)) DOI:10042/to-7182

From the calculated transition states, the C=C bond lengths are measured at 1.38 Å and the C-C bond length 1.40 Å. These values lie between literature values for C=C and C-C bond lengths: 1.30 Å and 1.54 Å respectively. This shows that what were previously π bonds are donating the electron density to σ bonds, the double bonds are becoming single bonds while the single bonds are becoming double bonds. This confirms the aromatic character of the transition state.

The HOMO and LUMO of the transition state have been plotted and can be seen in the table below.

Transition state frontier molecular orbitals

Molecular Orbital		Energy (a.u.)	Symmetry
LUMO		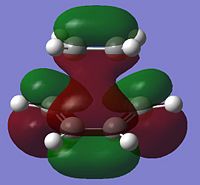0.023	Symmetric
HOMO		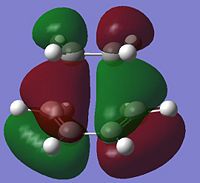-0.323	Anti-symmetric

The LUMO of the TS is formed from the symmetric LUMO of cis-butadiene and the symmetric HOMO of ethylene, and is symmetric itself. The HOMO of the TS is formed from the anti-symmetric HOMO of cis-butadiene and the anti-symmetric LUMO of ethylene, and is anti-symmetric itself. This analysis is in agreement with the conservation of orbital symmetry; where two orbitals must have the same symmetry to interact, and the resultant orbital must have the same symmetry. From looking at the HOMO there is a lot of electron density between the butadiene and ethylene where the new bonds are forming as expected. The transition state involves 6 electrons and will occur suprafacialy if under thermal conditions; it must have a Huckel transition state where the new bonds form from the same side of the molecule. The molecular orbitals generated here are only for this basis set, if another level of theory was used, the ordering of orbitals could change.

Activation Energy

The reactants were optimised using the B3LYP level of theory in order to make comparisons to the transition state energies. The optimised energy of ethylene and cis-butadiene was -78.523 a.u. and -155.996 a.u. respectively, the sum of which is -234.499 a.u. The difference in energy between the reactants and the transition state calculated earlier (-234.544 a.u.), the activation energy is 0.045 a.u. or 118.88 kJ mol^-1. This is in very good agreement with the literature value of 115 kJ mol^-1.

Cycloaddition of Cyclohexa-1,3-diene and Maleic Anhydride

Another very common example of the Diels-Alder reaction is between that of cyclohexa-1,3-diene and Maleic anhydride shown in the scheme below.

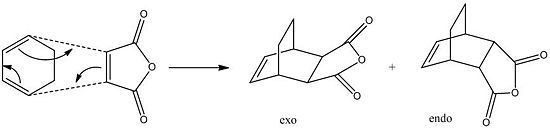
In this example there are two possible products, that being exo and endo, compared to the one seen before. The stereo outcome is dependant on the direction of attack by the dienophile, and the endo product is by far the major product. The observation that the endo product is formed is explained by the endo rule, which suggests that the transition state leading to the endo product is expected to be lower in energy than the exo transition state due to seconday orbital overlap.

Optimisation of exo and endo transition states

The transition states were optimised in the same way as the previous Diels-Alder example above. Both reactants were optimised using the AM1 method, then copied into the same window and arranged in a similar geometry to that expected for the transition states. The transition states were optimised at the semi-empirical AM1 level first with the distance between the two reaction centres frozen at 2.2 Å. Then it was optimised again with the distances unfrozen and the resulting conformation for the exo and endo transtion states are linked below. Finally the transition state was optimised at the higher B3LYP/6-31G(d) level of theory.

Comparison of Endo and Exo TS

Properties	endo		exo
	Semi-empirical/AM1	DFT/B3LYP/6-31G(d)	Semi-empirical/AM1	DFT/B3LYP/6-31G(d)
Energy (a.u.)	-0.0515	-612.683	-0.0504	-612.679
Imaginary Frequency (cm-1)	-806	-447	-813	-448
C-C Bond Forming Length (Å)	2.16	2.27	2.17	2.29

From the frequency analysis there is only one imaginary frequency comfirming the succesful location of the transition states. The vibration shows the synchronous formation of the two C-C bonds as seen in the previous example, which is what is expected for the concerted cycloaddition that is the Diels-Alder reaction. One might expect the exo product to be the most thermodynamically stable due to the least steric hinderance, however the Diels-Alder reaction is kinetically controlled and so the lowest energy transition state will determine the product. From the data above, the endo transition state has the most negative energy (endo-exo TS energy difference = 2.51 kcal/mol) meaning this transition state will be summounted fastest leading to the formation of the endo product, as observed experimentally. This difference in stability can be explained by secondary orbital overlap between the (O=C)-O-(C=O) fragment and the newly forming C=C double bond which isn't present in the exo product. The bond lengths are very similar between the two transition states, a small difference is seen for the C-C forming bond, the endo transition state having a smaller C-C bond by 0.02 Å which could be due to the secondary orbital interaction bringing the reactants slightly closer together compared to the exo. The output files are linked below.

Exo TS (semi-empirical AM1): DOI:10042/to-7200

Exo TS (DFT/B3LYP/6-31G(d)) DOI:10042/to-7202

Endo TS (semi-empirical AM1): DOI:10042/to-7201

Endo TS (DFT/B3LYP/6-31G(d)) DOI:10042/to-7203

The HOMO and LUMO orbitals were generated for both exo and endo transition states in an attempt to see the seconday orbital interaction, these could change based on the optimisation method used.

Molecular Orbital	endo			exo
		Energy (a.u.)	Symmetry		Energy (a.u.)	Symmetry
LUMO		-0.067	Anti-Symmetric		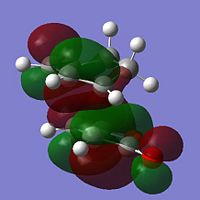-0.078	Anti-Symmetric
HOMO		-0.242	Anti-symmetric		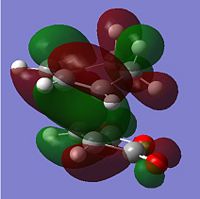-0.242	Anti-symmetric

It can be seen that the HOMO describes the forming σ bonds between the two reactants, seen by the large amount of electron density found between the relevant atoms whereas in the LUMO the orbitals between reactants are out of phase. The HOMO is formed from the interaction between the HOMO of the diene and the LUMO of the dienophile as seen before.

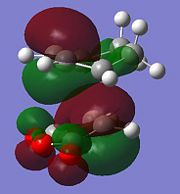
The observed outcome of the Diels-Alder reaction, that the endo isomer is almost exclusively formed, is commonly explained by secondary orbital overlap. This is a stabilising interaction between the (C=O)-O-(C=O) fragment orbitals and the newly forming C=C bond from what was the diene. The diagram below shows how this interaction is possible in the endo isomer but not possible in the exo isomer. These secondary orbital interactions are only stabilising interactions, they are not actually bonds being formed.

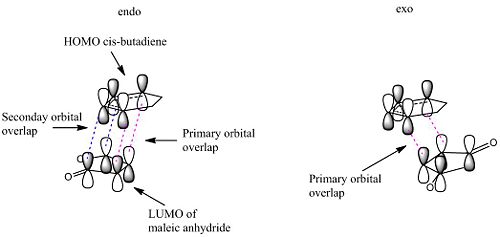
From this LCAO analysis we would expect to see a bonding type interaction between the newly forming C=C bond and the (C=O)-O-(C=O) fragment in the HOMO of the endo transition state, however this is not the case. In fact in the generated HOMO above we actually see a nodal plane. This could indicate inconsistencies with the theory on which this orbital interaction is based, however the more likely explanation is due to the level of theory being used to calculate the molecular orbitals. As the precise ordering of molecular orbitals can change depending on the method used, other molecular orbitals were looked at for evidence of the secondary orbital interaction this can be seen below. There are other reasons that may lead to the endo transition state having a lower energy, for example the exo transition state may have greater steric interactions as it points the same side as the bridge head.

This is the HOMO-1 which shows the new C=C bond forming on the diene and its possible to see signs of the secondary orbital overlap as the lobes are inphase with the (C=O)-O-(C=O) fragment

Conclusion

In this lab, computational techniques have successfully been used to model transition states and calculate properties, vibrations and orbitals for these transition states. This has allowed for the prediction of reactions which are not determined just by the energy of the final products, for example the endo selectivity of the Diels-Alder reaction. As with all computational chemistry there is a trade off between accuracy (level of theory used) and the time and computing power required. Also due to the errors associated with calculations, different methods can produce slightly different results/energies. Limitations include the fact that the calculations can't tell if a reaction occurs under thermo of kinetic conditions, also its possible there are solvent effects, or effects seen in bulk solution which are not taken into account when computing for a single molecule.