Rep:Mod:swinorg2

Module 2: Bonding

Scot Wheeler

Year 3 computational lab module 2

Introduction

This lab will demonstrate the uses of computational chemistry in predicting the structure of a variety of compounds and distinguishing between possible isomers. The possible different levels of accuracy will be explored and molecular orbitals will be calculated as well as the possible vibrations of the molecule. As with any technique, there are errors associated and they will be discussed.

BH₃

Geometry Optimisation

A BH₃ molecule was modelled in GaussView and the geometry optimised using the B3LYP method (which determines the type of approximations used) and 3-21G basis set (which is the accuracy of the calculation). There are two parts to the optimisation: firstly the SCF part which assumes nuclei position are fixed and Schrodinger equation is solved for the electron density; secondly the OPT part which solves for the position of the nuclei by changing the nuclei position and repeating SCF to determine the lowest energy state. Some key results of the optimisation are reported in the table below: log file

optimisation data

Property	Value
B-H bond length (Å)	1.193
H-B-H bond angle (o)	120
Calculation method	B3LYP
Basis set	3-21G
Final energy (a.u.)	-26.462
Gradient (a.u.)	0.000207
Point group	D3h

Importantly, the value of the gradient allows us to confirm the optimisation has been successful. Ideally this value should be zero indicating the energy doesn't change for small displacements but any value less than 0.001 is sufficient. A graph of total energy vs optimisation step shows a plateau as the energy tends to a constant value.

A 'Natural bond orbital analysis' was carried out and the NBO charge distribution was determined as: B = 0.332 and H = -0.111. As expected from the symmetry of the molecule all three hydrogen atoms had the same value while the overall charge was 0. It is also possible to extract information on the make up of the bond (44.5% contributed from boron)as well as the hybridisation for example boron: 33.3% s character and 66.6% p character suggesting sp² hybridisation. Meanwhile each Hydrogen atom contributes 55.5% to each bond which comes from a H orbital with 100% s character as would be expected.

Vibrational analysis

A frequency analysis was carried out on the optimised BH3 structure to confirm that a minimum in the potential energy surface has been found rather than a transition state (maxima). The frequency analysis is calculating the second derivative (the curvature) of the potential energy surface. If all vibrations are positive a minimum has been found, if one of the values is negative then a transition state has been found. The 'low frequencies' are also calculated and although usually 0, the inaccuracy in the calculation means they are non-zero however they tend to be an order of magnitude smaller.

Vibrational analysis of BH3 log file

No.	Vibration	Frequency cm-1	Intensity	Symmetry label
1	Vibration	1144	93	A"2
2	Vibration	1204	12	E"
3	Vibration	1204	12	E"
4	Vibration	2598	0	A1'
5	Vibration	2737	104	E'
6	Vibration	2737	104	E'

All the values for vibrations are positive, meaning a minimum has successfully been found. Although there are 6 vibrations (3N-6) it's not possible to distinguish all 6 peaks as vibrations 2 and 3 (1204 cm^-1) as well as 5 and 6 (2737 cm^-1) are degenerate, having the same frequency and thus overlap. Also vibration 4 has an intensity of 0 due to it being IR inactive as there is no overall change in dipole moment.

Molecular orbitals of BH₃

The molecular orbitals for BH3 were calculated using the optimised geometry found previously. The method was energy rather than optimisation and the MO analysis was 'switched on'. The first 8 molecular orbitals were calculated DOI:10042/to-6552 and are displayed in the table below:

Computed molecular orbitals of BH₃

	1	2	3	4	5	6	7	8
Computed MO's
Qualitative LCAO approach
Symmetry labels	1a'1	2a'1	1e'	1e'	1a"2	2e'	2e'	3a'1

The qualitative molecular orbitals derived from the linear combination of atomic orbitals are also shown as a comparison to that calculated. We can see there is a very strong match between those calculated computationally and those derived from the LCAO method suggesting that as a qualitative approach, LCAO is a good approximation. Differences arise in the ordering of the higher energy unoccupied orbitals; 3a'₁ is calculated higher in energy than 2e' compared to the LCAO approach. However this kind of difference is expected because LCAO is a qualitative approach which is limited in predicting the relative energy of the generated orbitals. Also computing the molecular orbitals allows us to look at those above LUMO+3 which is the highest one looked at with LCAO. For this relatively simple molecule, the similarity compared to that predicted shows that the 3-21G basis set used was sufficient however one might expect for a more complex molecule a higher basis set would be needed.

The MO diagram for BH₃ built up from H₃ fragment orbitals and a Boron atom:

TlBr₃

The molecule TlBr3 was drawn in GaussView and the geometry optimised in a similar way to BH3, DFT-B3LYP method however this time the point group was restricted to D3h with the tolerance set very tight and the basis set was LanL2DZ, a medium level basis set. This higher level basis set is required due to the heavier elements having more complex electronic structure. To save calculation time pseudo-potentials are used which model the core electrons as an effective potential rather than calculating for each electron. The method assumes that only valence electrons are involved. Key results are recorded in the table below: TlBr3 optimisation log file

optimisation data

Property	Value
Tl-Br bond length (Å)	2.65
H-B-H bond angle (o)	120
Calculation method	B3LYP
Basis set	LanL2DZ
Final energy (a.u.)	-91.218
Gradient (a.u.)	0.00000009
Dipole moment (Debye)	0.00
Point group	D3h

As can be seen from the gradient almost equal to 0 the optimisation has proceeded to a minimum. The calculated Tl-Br bond length of 2.65 Å is longer than that seen for BrH₃ above simply due to them being larger atoms with larger covalent radii. The calculated result is in good agreement with the literature value of 2.52 Å. The difference is due to the approximations used in the calculations. To confirm the optimised geometry is a minimum a frequency analysis was calculated. The same method and basis set is used as the frequency analysis is taking the second derivative of the potential surface. If the method or basis set was changed the result would be for a different potential surface, thus the results would not be comparable. The results are displayed in the table below:

Vibrational frequencies for TlBr₃ log file

Low frequencies cm-1	Normal Frequencies cm-1
-3.4	46
0	46
0	52
0	165
3.9	211
3.9	211

Firstly the low frequencies are close to 0 and much smaller than the normal frequencies calculated. This suggests the method and basis set are of an appropriate level. Secondly all the normal modes are positive confirming we have found a minimum.

Occasionally GaussView does not draw all the bonds within a molecule; this is because within the program there are set parameters that describe a bond. If the calculated bond length is greater than these parameters it is not considered a bond, this does not mean there is not one there as shown from the presence of vibrational frequencies.

A bond is not a physical line in space but an electronic interaction between molecules that leads to a lower energy than the two separate fragments. It is hard to define a point where a bond no longer exists as it is dependant on the molecules involved.

Isomers of Mo(CO)₄L₂

Mo(CO)₄(PPh₃)₂ can exist as both cis and trans isomers. The geometries were optimised and a frequency analysis computed to investigate the difference in properties, especially the CO vibrational bands which are symmetry dependant. To shorten computing time the phenyl ligands were replaced with chlorine atoms which are known to have similar electronic properties and are quite sterically demanding. Therefore Mo(CO)₄(Cl₃)₂ was investigated.

Optimisation

Both cis and trans isomers were modelled in GaussView and then optimised. They were each optimised twice at different levels due to the more complex electronic nature of the molecule. Firstly they were optimised using the DFT-B3LYP method and the low level basis set LANL2MB with the key words "opt=loose" to give a rough geometry that is generally known to give reasonable bond lengths and angles but less good with dihedral analysis. Secondly, the LANL2MB optimised geometries were optimised using the DFT-B3LYP method with the LANL2-DZ pseudo-potential and basis set with the key words "int=ultrafine scf=conv=9", after the structure had been edited to make sure one Cl atom from each PCl3 group was parallel with a CO axial bond. The optimised geometries and the output calculation files are here:

: DOI:10042/to-6621

: DOI:10042/to-6622

Key information regarding the optimised structures can be found in the table below:

Cis and Trans Mo(CO)₄(Cl₃)₂ LANL2-DZ optimisation summary

	Cis	Trans
File Type	.log	.log
Calculation Type	FOPT	FOPT
Calculation method	RB3LYP	RB3LYP
Basis set	LANL2DZ	LANL2DZ
E(RB3LYP) (a.u.) ±0.004	-623.577	-623.576
RMS Gradient Norm (a.u.)	0.00000496	0.00003074
Dipole Moment (Debye)	1.31	0.3052
Point Group	C1	C1
Mo-P distance	2.51	2.44
P-Mo-P angle	94.160	177.389

From the optimised structure, the reported Mo-P bond length for the cis isomer is 2.51 Å which is close to that reported in the literature 2.58 Å for the cis-Mo(CO)₄(PPh₃)₂. The calculated bond length for the trans isomer, 2.44 Å also relates well to 2.50 Å reported in the literature. Importantly, the bond length in the trans isomer is calculated to be shorter than the cis isomer as is observed experimentally. A possible reason for this is that elongation of the Mo-P bond in the cis isomer compared to trans arises to minimise steric interactions between the bulky Cl substituents.

The P-Mo-P bond angle in the cis isomer was calculated to be 94.2^o which is smaller than the experimental value of 104.6^o reported in the literature. This difference suggests that the optimised geometry calculated, although a minimum (see below), maybe a local minimum and not the lowest energy state of the molecule which would have been observed experimentally.

The trans P-Mo-P bond angle is expected to be 180.0^o but has been calculated at 177.4^o. Although different from experiment it is closer in value compared to the cis isomer maybe suggesting the optimised geometry is closer to that of the its true geometry.

The calculated energies of the cis and trans isomer are -623.577 au and -623.576 au respectively. This calculation says that the cis is lower in energy by 2.625 ±10 kJ mol^-1, a difference which is smaller than the error associated with the calculation method (~10 kJ mol^-1). Therefore these results are not reliable enough to conclusively say which isomer is lower in energy. The literature suggests that the trans isomer is likely to be lower in energy because of the higher steric clash between substituents present in the cis isomer. The optimisation completed here does not take into account the low lying d orbitals of the Phosphorous atoms which allow P to be hypervalent.

Frequency analysis

In order to confirm that the optimised geometry is a minimum, a frequency analysis was carried out. The result produced no negative frequencies therefore the location of a minimum was successful. Not all frequencies are reported here, just those corresponding to CO stretches and any low frequencies.

Low frequencies

Cis isomer DOI:10042/to-6665				Trans isomer DOI:10042/to-6666
Vibration	Frequency cm-1	Intensity	description	Vibration	Frequency cm-1	Intensity	Description
Vibration	11	0.0264	Conrotation of both PCl3 groups	Vibration	5	0.0941	Rotation of PCl3 in same direction, opposite to rest of molecule
Vibration	18	0.0074	Disrotation of PCl3 groups	Vibration	6	0.0000	Rotation of PCl3 groups in opposite directions

These low frequencies above are rotations of the PCl₃ groups, and the low frequency they occur at means they are likely to be occurring at room temperature k_BT=2.5 kJ mol^-1 = 207 cm^-1 with a large amplitude; when molecular collisions occur the translational energy to gets converted to vibrational energy.

The carbonyl stretching frequencies for both isomers are now reported and compared to that reported in the literature. There is a known error of 10% associated with the frequencies calculated due to the harmonic approximation used for bond oscillations instead of the more realistic anharmonic potentials.

CO stretching frequencies

Cis isomer					Trans isomer
Frequency cm-1	Intensity	Lit. frequency Mo(CO)4PCl3	Lit. frequency Mo(CO)4PPh3	Symmetry	Frequency cm-1	Intensity	Lit. frequency Mo(CO)4PCl3	Lit. frequency Mo(CO)4PPh3	Symmetry
1945	762.9	1986	1897	B2	1950	1475.4	1896	1902	EU
1949	1498.4	1994	1908	B1	1951	1466.8	1896	1908	EU
1958	632.8	2004	1927	A1	1977	0.6	-	-	B1g
2023	597.8	2072	2023	A1	2031	3.8	-	-	A1g

Firstly, from symmetry the cis isomer should have C_2v symmetry with the irreducible representation 2A₁ + B₁ + B₂, all of which are IR active. While the trans isomer with D_4h symmetry has irriducible representation A_1g + B_1g + E_u of which only E_u is expected to be IR active. Therefore we would expect to see 4 vibrations for the cis isomer and 1 vibration for the trans isomer. We see exactly as expected for the cis isomer, with 4 calculated peaks corresponding to CO stretches. While for the trans isomer, due to relaxed symmetry (reported as C₂) we also see four; however the two that occur at 1950 cm^-1 and 1951 cm^-1 are infact degenerate and appear as one absorption band. In the case of 1977 cm^-1 and 2031 cm^-1 these are expected to be IR inactive and only appear with a very small intensity due to the optimised geometry not having strict D_4h symmetry. In comparison to the literature there is a large difference. This is due to the systematic error of 10% associated with the calculation which is obviously more pronounced at higher frequencies.

Mini Project

Introduction

The presence of carbonyl ligands in a metal complex allows for easy analysis, not only of the structure as shown above but also the electronic properties. The complex Mo(CO)₃(PX₃)₃ was investigated with different X groups that will have an effect on the electronic properties of the PX₃ ligand. Computational chemistry has been used to verify the results seen in the literature which suggest that as the electron donor properties of X increase the CO stretching frequencies decrease. This type of computational analysis could be used in predicting the possible success of a ligand in 'fine tuning' the electronic properties of metal complex. Three PX₃ ligands have been investigated: PCl₃, PF₃ and PH₃

Optimisation

A similar method was employed to that above, the molecules were drawn in GaussView prior to the first optimisation using the DFT/B3LYP method and low level pseudo-potential LANL2MB basis set; with the "opt=loose" keywords to reduce the precision of the first optimisation. The log files were checked that the jobs had converged successfully and then the second optimisation was carried out. Firstly the dihedral angles were modified in the hope of finding a minimum as the dihedral angles calculated with the LANL2MB basis set tend not to be accurate. It was decided to treat two of the PX₃ ligands in the same way as the cis isomer example above, where one group had a Cl orientated parallel up with an axial CO and the second had one orientated parallel down. The third PX₃ group was rotated to a position that seemed sensible in terms of sterics. Then the second optimisation was completed with the same DFT/B3LYP method but now with the medium level LANL2DZ basis set. As before the convergence criteria was tightened by adding keywords "int=ultrafine scf=conver=9". Results from the second optimisation are displayed in the table below.

	Mo(CO)3(PCl3)3	Mo(CO)3(PF3)3	Mo(CO)3(PH3)3
	DOI:10042/to-6743	DOI:10042/to-6744	DOI:10042/to-6745
File Type	.log	.log	.log
Calculation Type	FOPT	FOPT	FOPT
Calculation method	RB3LYP	RB3LYP	RB3LYP
Basis set	LANL2DZ	LANL2DZ	LANL2DZ
E(RB3LYP) (a.u.) ±0.004	-561.605	-1325.825	-432.39
RMS Gradient Norm (a.u.)	0.00000733	0.00005113	0.00000913
Dipole Moment (Debye)	0.9183	2.9743	9.1924
Point Group	C1	C1	C1
Mo-P distance	2.53	2.48	2.62
Mo-C distance	2.01	2.02	1.97

Due to the change in atoms it's not possible to compare relative energies of the three molecules. When looking at the bond lengths, we see a general increase in the Mo-P bond as the electronegativity of the X substituent decreases: H > Cl > F. This is because the more electropositive the X substituent, more of the electron density is pushed onto the metal atom and away from the Mo-P bond. However it is surprising that the molecule with the smallest substituents has the longest bond, This goes against steric arguments. This is opposite for the Mo-C bond, which sees a decrease in the Mo-C bond length with decreasing electronegativity. This makes sense with our prediction as we expect that electron density is being increased between metal and carbonyl ligand (increased backbonding) which would have the effect to increase the bond order of Mo-C.

Frequency analysis

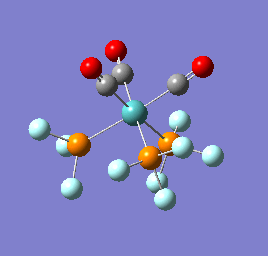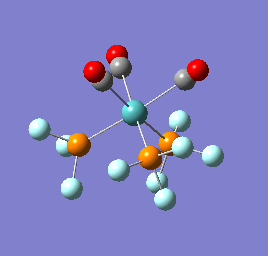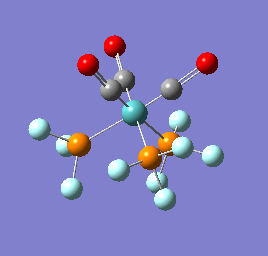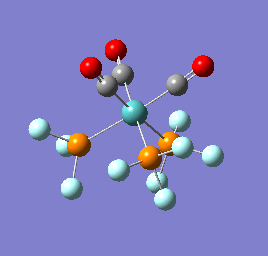
To confirm a minimum has been found and to investigate the stretching frequencies of the CO ligands a frequency analysis was completed on the optimised structures. The frequencies calculated for all three complexes were positive indicating that a geometry minimum has been found. The method was consistent with that used for the optimisations above, DFT/B3LYP with the LANL2DZ basis set. The point group of the molecule is C_3v and there are two peaks predicted for the stretching frequencies of each of the molecules

The three vibrations: E, E and A₁ are: , ,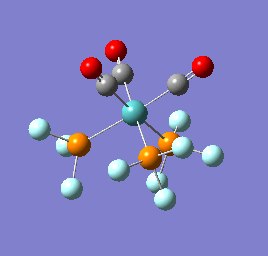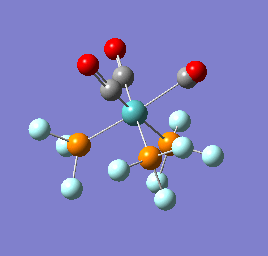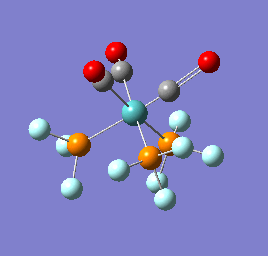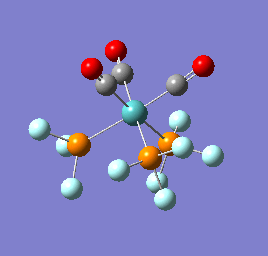

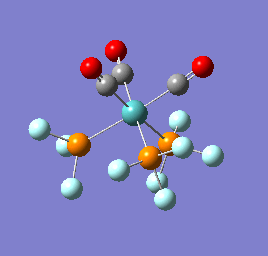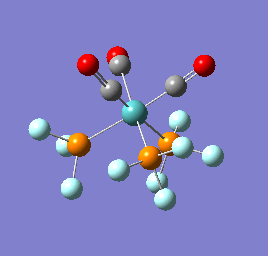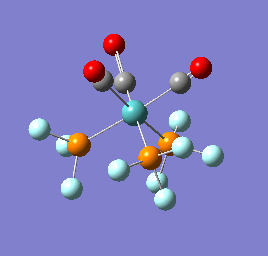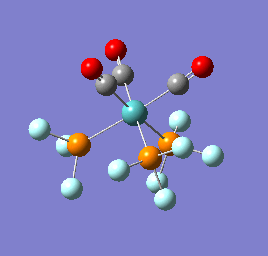CO stretching frequencies

Mo(CO)3(PCl3)3 DOI:10042/to-6888				Mo(CO)3(PF3)3 DOI:10042/to-6887				Mo(CO)3(PH3)3 DOI:10042/to-6886
Frequency cm-1	Intensity	Lit. frequency Mo(CO)3(PCl3)3	Symmetry	Frequency cm-1	Intensity	Lit. frequency Mo(CO)3(PF3)3	Symmetry	Frequency cm-1	Intensity	Lit. frequency Mo(CO)3(PH3)3	Symmetry
1947	658.08	1991	E	1968	766.86	2055	E	1835	1138.65	1892	E
1947	658.19	-	E	1968	767.35	-	E	1835	1138.61	-	E
1995	1124.09	2040	A1	2020	899.47	2090	A1	1915	941.34	1971	A1

It was predicted earlier that the stretching frequency of the CO ligands would decrease in wavenumbers as the electronegativity of the PX3 substituents decreased. It can be seen from the results of the frequency calculations above that, as the electronegativity decreases F (3.98) > Cl (3.16) > H (2.20) the carbonyl stretching frequencies decrease (eg vibrational symmetry E): F(2020 cm^-1) > Cl(1990 cm^-1) > H(1915 cm^-1). This observation is due to the donor properties of the phosphorus group. When the X atoms are highly electronegative, Fluorine, the PF3 group is a bad electron donor. Therefore there is a low amount of electron density located on the metal centre and consequently the ability to backbond with the carbonyl ligand is low. When the X atoms are exchanged for more electropositive, Hydrogen, the electron donor ability of PX3 is increased. Electron density is pushed onto the metal centre which means it is available for backbonding between the metal d-orbitals and the antibonding C=O bond. As electron density is pushed into the carbonyl antibonding orbital, the bond order is reduced and hence the strength of the bond is also reduced. This is observed by a decrease in the energy of the bond vibrations.

In comparison to the literature, the trends observed are in good agreement however due to the 10% error associated with the calculated values, there is a difference between the values calculated and that observed experimentally. This is due to the harmonic approximation employed as oppose to using an anharmonic potential. As the first two vibrations for each molecule occur at the same frequency, only two peaks are observed which is what is expected.

The above optimisation and frequency analysis was completed with the LANL2DZ basis set, this does not take into account the possible use of d orbitals for the P atom. To investigate the difference this has, the optimisations and frequency analysis was re-run just for Mo(CO)₃(PCl₃)₃ this time with the added keyword "extrabasis" and the input file edited to instruct the program to add d functions to the P atoms. As the method has been changed it's not possible to compare energies, however the CO stretching frequencies are almost identical to that for the previous method: 1940 cm-1, 1940 cm-1 and 1991 cm-1, differences of 7, 7 and 4 respectively. This shows that the inclusion of the d orbitals on P has very little effect on the CO stretching frequencies which are of interest here. The calculated bond lengths are also very similar, the largest difference being that of Mo-P which shows a decrease from 2.53 Å to 2.49 Å when the d orbitals are included. This is possibly due to an interaction with the metal d orbitals. The Mo-C bond is very similar at 2.02 Å. The optimisation and frequency output files are located DOI:10042/to-6905 and DOI:10042/to-6904 respectively.

It was realised that the LANL2DZ basis set was not needed for all the atoms within the molecule as the basis set is for heavy atoms. Therefore the optimisation and frequency analysis was computed again with a mixed basis set, LANL2DZ for Mo and 6-311G(d,p) for the other atoms.

Output files:

Mo(CO)₃(PCl₃)₃: Optimisation DOI:10042/to-6952 , Frequency DOI:10042/to-6950

Mo(CO)₃(PF₃)₃: Optimisation DOI:10042/to-6953 , Frequency DOI:10042/to-6949

Mo(CO)₃(PH₃)₃: Optimisation DOI:10042/to-6951 , Frequency DOI:10042/to-6948

CO stretching frequencies mixed basis set

Mo(CO)3(PCl3)3 frequencies cm-1	Mo(CO)3(PF3)3 frequencies cm-1	Mo(CO)3(PH3)3 frequencies cm-1
2074	2091	1992
2074	2091	1992
2119	2139	2057

We do see a difference between those calculated with the mixed basis set compared to those above which were calculated using LANL2DZ on all the atoms, but this difference is within the error associated with frequency calculations. The same trend is observed; the largest CO frequencies (least backbonding) are when PF₃ co-ligands are present whereas the lowest frequencies (most backbonding) are when the PH₃ co-ligands are present for the same reasons as discussed above. The literature value are fairly well placed between the two methods so no real indication can be made as to what method was more accurate.

MO analysis

The molecular orbitals of the Mo(CO)₃(PCl₃)₃ were calculated from the optimised structure above employing an energy calculation with the added keywords pop=full.

HOMO and HOMO-1 molecular orbitals

Mo(CO)3(PCl3)3 DOI:10042/to-6936	Mo(CO)3(PF3)3 DOI:10042/to-6937	Mo(CO)3(PH3)3DOI:10042/to-6938
HOMO
HOMO - 1

Firstly we can see that the CO antibonding orbitals contribute to the HOMO and HOMO-1 orbitals of the three molecules investigated. This demonstrates that backbonding between the metal and the carbonyl ligands occurs, due to them being part of the molecular orbitals which are filled with electrons. Secondly and most importantly is the trend that is seen, especially in the HOMO. For Mo(CO)₃(PF₃)₃ we see electron density located on the P atom as expected due to the high electronegativity of the F atoms, pulling electron density away from the metal center. Now looking at Mo(CO)₃(PCl₃)₃, we would expect to see less electron density on the P atom and more on the metal centre compared to F due to Cl having a smaller electronegativity. This is exactly what is seen, the P atoms (yellow) are now visible behind the MO surface. Lastly, for Mo(CO)₃(PH₃)₃, the most electropositive PX₃ ligand, we see the least electron density located on the P atom. A decrease in electron density on the P ligands means increased electron density on the metal centre, thus more backbonding with CO, weaker CO bonds and lower frequencies which is exactly what is seen above. Therefore the MO analysis is in good agreement with the other data already presented and gives a nice visual representation of the effects the different ligands have.

Further investigations

NBO analysis from the MO output files would maybe give a more numerical view to the exact bonding within the molecule in the same way as it was used in the BH₃ section. Possible further investigations could include looking at the effect that the metal centre has on the backbonding, likely to be dependant on the size of the metal d orbitals and the electron density found on it which could be effected by a possible charged species.

Conclusion

In this lab module it has been demonstrated how computational chemistry can be used to model numerous compounds, optimise them with numerous levels of accuracy to find a minimum energy geometry and use frequency analysis to confirm a true minimum has been found. The molecular orbitals have been generated and natural bond orbital analysis has been used to give quantitative results of the bonding within a molecule. Two isomers were investigated but it was found that the energy difference was smaller than the error associated with the calculation, but the carbonyl stretching frequencies were in agreement with those found in the literature. For the miniproject, the electronic properties of Mo(CO)₃(PX₃)₃, X = H, Cl, F, were investigated by analysis of the backbonding present between the Mo centre and the CO ligands from the CO stretching frequencies. The results were in agreement with literature values and the trend that as the electronegativity of the PX₃ ligands decrease, the amount electron density on the metal centre increases, backbonding increases and it is observed as a decrease in the CO stretching frequencies.