Rep:Mod:swheeler1

Module 1: The basic techniques of molecular mechanics and semi-empirical molecular orbital methods for structural and spectroscopic evaluations

Scot Wheeler

Year 3 computational lab module 1

Introduction and Aims

It is possible to use numerous computer techniques to model aspects of structure and reactivity of a variety of organic compounds, allowing the rationalisation of observed reactions and prediction of new reactions. This module is focused on the technique of molecular modelling, a simple yet powerful technique that allows the prediction of certain molecular properties through the summation of individual bond properties rather than the need to solve explicit wave equations quantum mechanically. It is assumed that the energy of a molecule comprises of: the sum of all diatomic bond stretches, triatomic bond angle deformations, tetra-atomic bond torsions, non-bonded Van der Waals repulsions and electrostatic attractions of individual bond dipoles.

Essentially it is an interpolative technique which relies on well characterised data and known molecules, meaning it becomes less accurate when knowledge of electron density within a molecule is a needed.

Modelling using Molecular Mechanics

The Hydrogenation of Cyclopentadiene Dimer

Dimerisation

At room temperature cyclopentadiene dimerises via a [π4s+π2s] cycloaddition Diels-Alder reaction, producing either the exo (1) or endo (2) products. :

Cyclopentadiene [4+2] Diels-Alder

The relative stabilities of the products can be determined by modelling them and optimising the geometries to give the lowest energy. The product with the lowest energy is thermodynamically the more stable. The procedure was carried out in Chem3D using the MM2 force field option. The results are shown below:

Molecule	Energy kcal/mol
exo (1)	31.88
endo (2)	34.00

These calculations show that the exo product is lower in energy than the corresponding endo product by 8.87 kJ mol^-1, the exo product is therefore the most thermodynamically stable and would be the product expected if the reaction was under thermodynamic conditions. However, because the Diels-Alder reaction is under kinetic control this is not the case, it was observed that the endo product is always formed. This is explained by the endo rule and arises due to the transition state for the endo product being lower in energy than that of the exo product, therefore it is formed faster. The lower transition state for the endo product is due to a stabilising secondary orbital interaction between the p_z orbitals of the inactive double bond and the forming double bond. As molecular mechanics is unable to account for such interactions due to an inability to investigate transition states that involve bond breaking/forming we see a limitation of such a technique.

Hydrogenation

hydrogenation of endo isomer

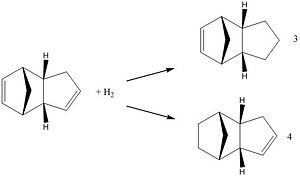
The endo product can be hydrogenated at either of the two alkene bonds to give the two products to the right. Further hydrogenation leads to the tetrahydro product.

Again using Chem3D the products were modelled and their geometries optimised to give the lowest energy, which on comparison of the two will allow us to determine the most (thermodynamically) stable product. The relative energies of the two hydrogenated products are shown in the table to the right:

From this data it is clear that molecule 4 is the most thermodynamically stable, a difference in energy of 19 kJ mol^-1 compared to molecule 3. Hydrogenation of the double bond that leads to molecule 4 indicates the molecule becomes more stable than the endo dimer. The energy calculated for the endo dimer was 34.00 kcal mol^-1 which is reduced to 31.16 kcal mol^-1 upon hydrogenation while the hydrogenation of the other double bond leads to an increase in energy to 35.70 kcal mol^-1 which is thermodynamically unfavourable; therefore we would expect molecule 4 to be easier to form. To achieve the tetrahydro product, extended reaction times would be expected.

Hydrogenation products of the endo isomer

	Molecule Energy kcal/mol
Energy Contribution	Molecule 3	Molecule 4
Stretch	1.27	1.10
Bend	19.81	14.56
Stretch-Bend	-0.83	-0.55
Torsion	10.87	12.50
Non-1, 4 VDW	-1.22	-1.10
1, 4 VDW	5.64	4.50
Dipole/Dipole	0.16	0.14
Total Energy	35.70	31.16

A breakdown of the contributions to the total energy is also displayed, from which it is possible to see where the difference in energy originates from. The largest difference comes from the bending energy: 19.81 kcal mol^-1 for molecule 3 compared to 14.56 kcal mol^-1 for molecule 4. The lower bend energy in molecule 4 is due to the relief of ring strain through hydrogenation of the double bond in the norborene unit. The ring strain is still present in molecule 3 as the norborene double bond forces the bond angle to be unfavourable. These results are in agreement with the observed experimental result.

Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD⁺ analogue).

Molecule 5 is an optically active derivative of proline, it reacts with methyl magnesium iodide with absolute stereochemistry forming the alkylated product 6:

The starting material can be modelled using molecular mechanics and by starting from a variety of slightly different geometries it is possible to find the most stable reactant. The geometries were altered by changing the position of the atoms, or building the molecule in different ways whilst minimising the energy at each step (eg building up from either pyridine or from pyrollidine ends). The geometry of the carbonyl group is likely to be an important factor so the dihedral angle relative to the plane of the pyridinum ring has been measured.

Energy against carbonyl group-pyridinium ring dihedral angle - Molecule 5

Dihedral angle	Total Energy kcal/mol
11o	43.13
23o	35.69
8o	43.16
33o	280.97

As can be seen from the data, the dihedral angle between carbonyl groups and ring has a large effect on the overall energy, importantly the carbonyl group is always found to be above the plane of the ring, no stable conformations are found with the carbonyl group below the plane. The reaction is likely to proceed via coordination of the magnesium in the Grignard reagent with the carbonyl oxygen followed by the nucloephilic attack of the methyl group at the 4-position which must occur on the same face as the magnesium is coordinated.

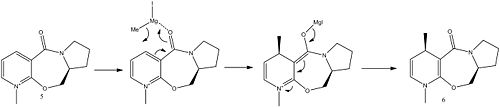
From the structure of the lowest energy geometry found, dihedral angle of 23^o it is clear the least sterically hindered side is the top face despite the carbonyl being angled toward the top face, therefore coordination of the Grignard reagent, via the magnesium atom, will occur on the top face leading to the attack of the nucleophilic methyl group from the same face, and therefore to the absolute stereochemistry observed.

Molecule 5
Molecule 5

It is not possible to include the MeMgI component in the calculation because when the program performs a force field calculation it takes into account the 'atom type' and uses known properties, for example a carboxyl carbon is treated different to an alkyl carbon. When the calculation is attempted with MeMgI, an error message appears stating the 'atom type' for Mg is not defined.

A closely related reaction of a pyridinium ring with aniline is shown below:

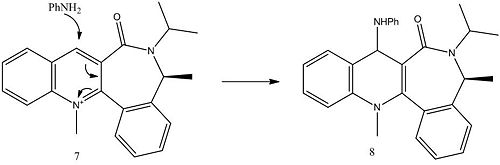
The molecule was modelled in the same was as before, optimising from numerous starting points, the results are shown in the table below.

Energy against carbonyl group-pyridinium ring dihedral angle - Molecule 7

Dihedral angle	Total Energy kcal/mol
25o	83.95
-20o	62.64
-24o	64.04
-65o	232.90

The lowest energy geometry now has the carbonyl group angled below the plane of the ring at an angle of -20^o and energy of 62.64 kcal mol^-1 and is shown in the link below.

The nitrogen with a lone pair is acting as the nucleophile in this reaction, and we would expect attack on the least hindered face of the ring to be favoured as coordination with the oxygen does not occur. As the lowest energy conformation has the carbonyl group 20^o below the plane of the ring, the attack is expected from the opposite (top) face and thus the stereochemistry shown above is expected. This is the opposite to that seen for molecule 5 as the Grignard reagent coordinated to the oxygen atom. The carbonyl group has the largest effect out of all the substituents as it's located closest to the C4 reaction centre. This result is in agreement with the literature which shows that the product is formed as a single diastereomer controlled by the geometry of the lactam carbonyl group.

One way to improve the model would be to use a modelling technique other than molecular mechanics where more than one molecule can be taken into account. The MOPAC molecular orbital method, which will be used later, takes into account the electronic properties ie. molecular orbitals of the molecules giving a far greater accuracy.

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

Molecules 9 and 10 are intermediates in the synthesis of Taxol and are synthesised as two isomers with the carbonyl either up or down. Over time, 9 isomerises to 10 but due to a high energy barrier for rotation of a particular bond, the isomers can be isolated. This is an example of atropoisomerisation, which usually arises due to high steric demand which stops free rotation.

Intermediates in the synthesis of taxol

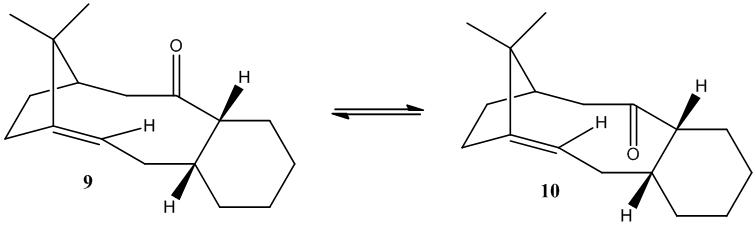
The lowest energy atropisomer was calculated using both MM2 and MMFF94 and the results are shown in the table below. The cyclohexane ring was modelled in the chair conformation which gave the lowest energy. On attempting to rearrange to other known conformations (eg. twist boat) the molecule always returned to the chair conformation.

Relative energy of taxol intermediate isomers

	Molecule Energy kcal/mol
Energy Contribution	Molecule 9	Molecule 10
Structures
Stretch	2.67	2.55
Bend	15.85	9.82
Stretch-Bend	0.39	0.27
Torsion	18.30	19.47
Non-1, 4 VDW	-1.15	-1.44
1, 4 VDW	12.69	12.62
Dipole/Dipole	0.15	-0.19
Total Energy MM2	48.91	43.12
Total Energy MMFF94	70.54	61.20

As can be seen from the data above, molecule 10 has the lowest energy for both MM2 and MMFF94 force-fields. The difference between methods is because the energies generated are relative, so direct comparison is not possible between force-fields although the general result that molecule 10 is lower in energy than molecule 9 still holds true.

Whilst the different cyclohexane conformers have a large effect on the energy of the molecule, both of the above geometries have the chair conformations. The greatest difference in the constituent parts of the total energy is the bending energy, 15.85 kcal mol^-1 for molecule 9 compared to 9.82 kcal mol^-1 for 10. This difference can be attributed to the angles of the carbonyl sp² carbon. The angles between the two R groups are:

	Molecule 9	Molecule 10
Bond angle	126o	118o
Bend Energy kcal mol-1	15.85	9.82

The ideal angle for an sp² carbon is 120^o hence why molecule 10 has a much lower bending energy than that of molecule 9 as the angle in 10 is much closer to ideal. Also from looking at the structures linked above, one would expect more steric clash in molecule 9 between the carbonyl group and the ring bridge. Due to these interactions, molecule 10 has the lowest energy and thus is the thermodynamic product which you would expect molecule 9 to isomerise to.

One might expect that the functioanlisation of the alkene would be a favoured reaction due to it being a strained alkene, however it is reported to be abnormally slow. The reason for this is due to it being a hyperstable alkene, these are defined as an alkene which has a lower energy (less strained) than the corresponding hydrogenated single bond form and thus show abnormally low reactivity. The hyperstable alkene arises due to the particular ring size it is part of, and the position of the bridgehead causes a twisting of the alkene double bond, reducing the π overlap, thus reducing the HOMO - LUMO gap .

Modelling using Semi-empirical Molecular Orbital Theory

Some of the limitation of molecular mechanics have been discussed above, these mainly revolve around the fact that the approach cannot handle problems that require the consideration of electrons within a molecule, for example the secondary orbital overlap which explains the endo selectivity in the Diels Alder reaction. Semi-empirical Molecular Orbital Theory allows for these electronic properties to be taken into account.

Regioselective addition of Dichlorocarbene

Part 1: Orbital control of reactivity

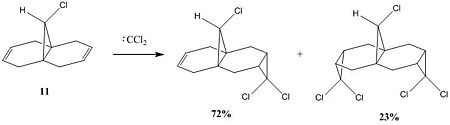
The addition of dichlorocarbene to compound 11 proceeds to give two products, the regiospecific mono-adduct and the di-adduct shown in the reaction scheme below.

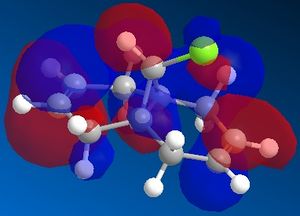
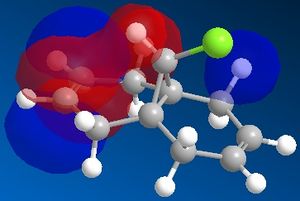
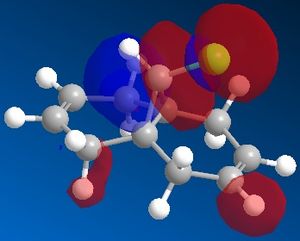
The reactivity of a molecule tends to be based on the frontier molecular orbitals, it's HOMO and LUMO. Using the electronic method MOPAC/PM6 in ChemBio3D, the approximate molecular orbitals have been modelled to describe the regioselectivity seen above.

Molecular Orbitals for compound 11

HOMO-1	HOMO	LUMO	LUMO+1	LUMO+2 !

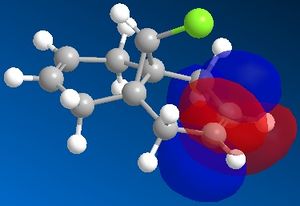The reaction of molecule 11 with an electrophilic dichlorocarbene would be expected to involve the most nucleophilic molecular orbital, the HOMO of the diene. As can be seen from the above molecular orbital pictures, the HOMO is located on the syn-alkene, hence the majority of the electron density is located on the syn alkene making it much more susceptible to electrophilic attack by the dichlorocarbene. This is in agreement with the observation that the only mono-adduct produced is the syn substituted product.

It it also possible to explain it from the opposite viewpoint,that the stability of the anti-alkene is due to a stabilising interaction between the LUMO+1, which represents the empty C-Cl σ* bond and the HOMO-1, which represents the filled anti C-C π bond. This mixing leads to a decrease in the HOMO-1 energy, stabilising the double bond further. Any electrophile will always react first with the syn alkene.

Part 2: Vibrational Frequencies

To investigate the vibrational frequencies within molecule 11 (dialkene), which has the double bond anti to the C-Cl bond, and a second molecule (monoalkene) with the anti-double bond hydrogenated to the single bond, a density functional approach is undertaken. This involves using a B3LYP/6-31G(d,p) Gaussian geometry optimization and frequency calculation and the results for the C=C and C-Cl stretches are shown below:

C=C and C-Cl stretching frequency data for molecule 11, 12 and derivatives

	Stretching frequency cm-1
syn-C=C	1757.37	1758.06	1757.65	1754.91
anti-C=C	1737.13	N/A	1797.55	1633.84
C-Cl	770.92	774.96	758.82	769.94

The vibrational frequencies observed in the IR spectrum and tabulated above are very similar between the molecules as expected, except for the lack of the anti C=C stretch in the hydrogented product. They are also in good agreement with accepted IR ranges of 600-800 cm^-1 for C-Cl, but higher than that expected for C=C: 1620-1680 cm^-1. The differences are likely due to the accuracy of the procedure and could be improved with larger basis sets and full quantum analysis, but this requires greater computing power and time.

The frequencies for both C-Cl and syn-C=C are shifted to higher wavenumbers with the removal of the anti alkene bond: 771 cm^-1 to 775 cm^-1 for C-Cl and 1757 cm^-1 to 1758 cm^-1. The difference is greater for the C-Cl bond because it is involved in the stabilising interaction of the LUMO+2 and HOMO-1 which is not present in the hydrogenated product. This means less electron density in the σ* C-Cl, thus a stronger bond, higher frequency. This provides proof of the stabilising interaction described above. Altering the anti-C=C bond in the ways above has little effect on the syn-alkene.

Taking this further, the substituents on the anti-alkene were modified and replaced by OH and SiH3; and the stretching frequencies calculated again with the results displayed above. There is very little difference between the stretching frequency for the syn C=C between molecules, but there is a large difference seen for the anti C=C to which the substituents are attached. The addition of the OH group acts to strengthen the C=C bond, seen by a higher stretching frequency, due to the resonance donation capability of the oxygen atom. The silyl group has the opposite effect, weakening the bond due to it's ability to accept electron density from the alkene. The effect on the C-Cl bond is smaller, the hydroxy group acts to weaken the bond slightly maybe due to increased electron density on the anti C=C bond available for interaction with the C-Cl σ*.

Structural based mini project using DFT-based molecular orbital methods

The claisen rearrangement was the first sigmatropic rearrangement to be discovered and occurred when an aryl allyl ether was heated without solvent to produce an ortho-allyl phenol. The first step is a [3,3]-sigmatropic rearrangement followed by proton transfer to restore aromaticity. It can be particularly challenging to predict the regioselectivity of the claisen rearrangement for a meta substituted aryl allyl ether and this paper is interested in improving the predictions possible through NMR analysis to determine the conformational preference of the reactant:

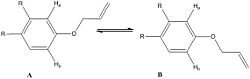
It is claimed within the paper that the reaction below shows 100% regioselectivity in favour of product C and reports the ¹³C NMR spectrum which show differences between the two. Using the methods above the geometries of both regioisomers were minimised at the mpw1pw91/6-31(d,p) level, after which the ¹³C NMR was calculated and compared to that reported in the literature. The ¹³C NMR was then calculated for the other isomer (D), and compared to that of the first to determine whether ¹³C NMR is a viable technique for distinguishing between the two regioisomers.

¹³C NMR

Calculated and reported experimental ¹³C NMR data for the two regioisomers C and D

Carbon atom	Molecule C calculated (ppm)	Lit 1 (ppm)	Lit 2 (ppm)	Lit 3 (ppm)	Molecule D calculated (ppm)	Carbon assignments
12	33.5	21.1	29.3	29.2	36.0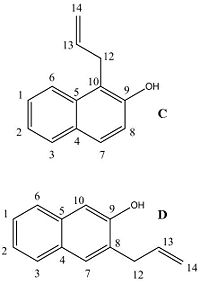
10	112.8	34.4	116.8	116.9	105.0
8	115.7	109.3	117.9	117.9	126.2
14	116.4	113.5	116.0	115.8	117.3
6	119.0	116.5	123.2	123.1	122.3
2	119.3	123.4	123.0	123.0	119.7
1	123.2	130.6	126.5	126.4	122.7
4	124.3	136.2	129.4	129.4	124.0
3	126.1	149.9	128.6	128.5	124.7
7	126.6	154.7	128.3	128.3	126.0
5	128.5	170.0	133.2	133.2	128.7
13	136.2		135.7	135.8	133.5
9	151.3		151.2	151.1	148.2
	DOI:10042/to-6483				DOI:10042/to-6484

The calculated ¹³C NMR data for isomer C as displayed in the table above was compared to the original literature . On comparison it was realised that: firstly not all the carbon atom shifts have been reported, possibly due to signals being very close in their ppm values; secondly the shifts have not been reported with the corresponding carbon atom that gives rise to the peak, which doesn't allow for the direct comparison of the calculated values; and thirdly although the solvents used for ¹³C NMR are reported as either CDCl₃ or d₅-pyridine it is not explicitly indicated which this particular ¹³C NMR was run in, although it's likely to be CDCl₃ as the ¹H NMR was in CDCl₃. In general it can be seen that the experimental literature spectrum differs from that calculated. Two peaks are reported below 40 ppm (21 and 34 ppm) whereas in that calculated here only one peak at 33.5 ppm is expected. Also a peak is reported at 170 ppm, which seemingly has no corresponding peak in the calculated data.

To determine whether the calculated NMR is wrong, or the literature NMR is incorrectly reported other literature which reported the ¹³C NMR of molecule C were investigated. Two examples of this are shown in the next two columns of the table above: lit 2 and lit 3 . These gave the solvent as CDCl₃ and comparing them to each other show a very strong correlation hopefully meaning they a reliable source as to what the experimental ¹³C NMR of the molecule is. Comparing these to the calculated ¹³C NMR it can be seen that there is a much closer match to that of the original piece of literature. This result would suggest that actually the calculated NMR data is correct and gives with reasonable accuracy a good prediction of the ¹³C NMR. Whilst the original literature (lit 1), which is already poorly characterised in terms of solvent used and the carbons responsible for the shifts, has been reported wrong or incorrectly acquired.

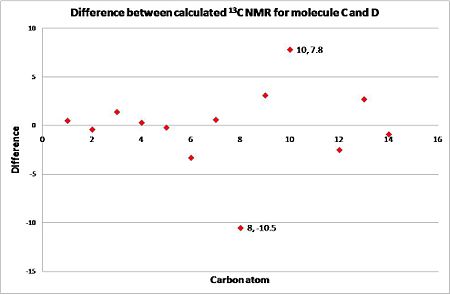
To show that ¹³C NMR is a viable technique for distinguishing between the regioisomers, the NMR for the second isomer (molecule D) was calculated in the same way as before, first applying a mpw1pw91/6-31(d,p)energy/geometry minimisation followed by calculation of the ¹³C NMR. The resulting data is displayed in the table above, the key differences are highlighted in the yellow cells. When the allyl group is attached it cause a higher ppm than when it is not: firstly a difference of 7.8 ppm is observed for carbon atom 10, to which the allyl group is attached in molecule C (112.8 ppm) and not in D (105.0 ppm), and secondly a difference of 10.5 ppm for carbon atom 8, to which the allyl group isn't attached in isomer C (115.7 ppm) but is in isomer D (126.2 ppm). These variations will allow for the identification of the isomer, therefore ¹³C NMR can be used to distinguish between the two possible isomers. It should also be noted that the position of the allyl group has an indirect effect on the chemical shift of carbon labelled 6, which shows a smaller chemical shift (119.0 ppm) when the allyl group close by (attached to C-10) and a higher chemical shift (122.3 ppm) when the allyl group is on the opposite side (attached at C-8).

IR

The IR spectra were calculated and as expected appeared very similar, showing that in this case the technique cannot be used to distinguish between the two regioisomers.

Regioisomer C
Regioisomer D

Regioselectivity

The literature is concerned with the difficulty in predicting the outcome of the Claisen rearrangement, especially relating to the effects of substituents. It reports that isomer C is formed in 100% yield over isomer D and that there is a link between the ratio of the reactant conformation (A and B, A -> C, B -> D) above and the observed regioisomer. For example, for the napthaline reaction above, the ratio of A to B is 11:1 and as mentioned before C is observed in 100% yield. To investigate the preferred conformation of the reactant geometries they were modelled and their energies calculated via MM2 and are reported in the table below:

Relative energy of reactant conformers A and B

	Molecule Energy kcal/mol
Calculation method	Reactant A	Reactant B
Total Energy MM2	2.6178	2.6258

As can be seen from the data, conformer A, that leads to the formation of the observed product C, has a slightly lower energy than that of B which supports the fact that A is the favoured geometry seen by the 3:1 ratio quoted in the literature.

The energies of the regioisomer products where also determined from the optimised mpw1pw91/6-31 (d,p) calculation that was used for the ¹³C NMR data. The Energy of product C was reported as -577.70942 au, while isomer D energy was reported as -577.71171 au. This gives an energy difference of -2.29 x 10^-3 au = -1.45 kcal mol^-1 in favour of product C. These results are in agreement with that observed in the literature, that A is the thermodynamically more stable reactant and forms isomer C which is the thermodynamically more stable product. The reported reaction is exothermic, and according to Hammond's postulate the transition state resembles that of the reactant. Although a very basic assumption, it could be assumed that the transition state between A and C is lower in energy than that between B and D, however the exact computational calculations for transition states forms the basis of the third part of this computational lab.

Conclusion

In conclusion this module has demonstrated the use of both molecular mechanics and semi-empirical molecular orbital theory as relatively quick and simple ways to accurately explain both reactivity and stereoselectivity. ¹³C NMR and IR spectra have been calculated and results have been shown to agree closely with that observed experimentally and therefore demonstrates how computational techniques can be used in predicting and verifying experimental results.