Rep:Mod:svp

Introduction

The aim of this experiment was to characterise transition states for the Diels Alder cycloaddition and Cope rearrangement, computationally using the GaussView program. By doing so transition structures and the preferred reaction mechanism could be elucidated for both.

The Cope Rearrangement Tutorial

Cope Rearrangement

The following tutorial analysed the reactivity of 1,5-hexadiene in the Cope rearrangement. The Cope rearrangemnet belongs to a class of reactions called pericylcic reactions. The mechanism by which the diene rearranges has previously been a topic of debate, owing to many computational and experimental studies. 1,5-hexadiene undergoes a [3,3]-sigmatropic shift in a concerted fashion. The diene passes through either a chair or boat transition structure, the latter lying several kcal mol^-1 higher in energy . Computational studies before have been ambiguous, making an agreement upon the mechanism difficult due to the flatness of potential energy surfaces belonging to the boat and chair transition states.In the following experiment activation energies were calculated at the HF/ 3-321G and the more sophisticated B3LYP/6-31G* level of theory. The latter uses the more accurate density functional theory (DFT) method. This method/basis set produces energies that comply with experimental data.

Nf710 (talk) 22:59, 18 November 2015 (UTC)It would have been nice here if you could have shown some understanding of the different methods. such as the fact that HF uses a mean field to describe the electron-electron repulsion which after over estimates this etc.

Optimising the Reactants

The “Anti2” conformation of 1,5- hexadiene

In Gaussview an “anti2” 1, 5- hexadiene molecule was built in an anti-peri-planar conformation. The molecule was cleaned before an optimisation was run at the Hartree Fock, 3-21G level of theory. This optimisation is run often as a pre-requisite to the more computationally expensive DFT (6-31G*) method. Cleaning before optimization adjusts the geometry of the molecule in accordance with a set of parameters designed to produce a molecule that would be expected chemically .Once the optimization was finished and all of the calculations had converged, the structure was symmetrized and the point group was found to be Ci. The energy of the molecule was found to be -231.69 a.u; this is in accordance with the energy provided in lab script appendix.

Structure	Point group	Energy/ Hartrees HF/3-21G
	Ci	-231.69253522

The “Gauche3” conformation of 1,5- hexadiene

Similarly to the anti-conformation the “gauche3” conformation was built and optimized at the Hartree Fock, 3-21G level of theory. The resultant energy was found to be less than the anti conformation and the given point group was C1 after symmetrising the molecule. The energy was again in agreement with the lab script value.

Structure	Point Group	Energy/ Hartrees HF/3-21G
	C1	-231.69266122

When calculating activation energies the lowest energy conformer of the reactant is used as a starting point. Intuition would indicate that the “anti 2” conformation of 1,5- hexadiene would be the lowest in energy, due to steric effects, this conformation leads to the least steric repulsion due to the dihedral angle. Studies however, and the results above, have found the “gauche 3” conformation to be the most stable. It has been suggested that this is due to an interaction between the vinyl proton and the c-c π electrons; the bonding interaction accounts for the extra stability of the gauche conformation. This effect is termed as the “CH-π” interaction .

Nf710 (talk) 23:03, 18 November 2015 (UTC) this is good use of literature. You could have shown this yourself however if you would have looked in the .chk file to show the orbitals and there is clearly favorable secondary orbital interactions between the two pi systems.

DFT Optimisation of Reactants

The "Anti 2" 1,5- hexadiene molecule was re-optimised using the B3LYP/6-31G(d) level of theory using the DFT method. This is a higher level of theory than the Hartree fock 3-21G method; which is often done as a prerequisite to reduce the computational expense associated with the higher level of theory. After the second optimisation the point group of the molecule remained Ci. The energy was found to be -234. 61 a.u. in agreement with the value provided in the lab script appendix.

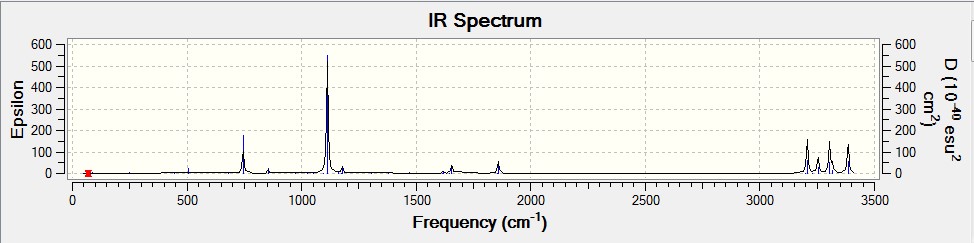
In order for the computed energies of the hexadiene molecules to be comparable with experimental data, a frequency calculation was completed. After-which it was then possible to identify the critical point (a point at which all vibrational frequencies are real and positive). A frequency calculation was conducted on the 6-31G(d) optimised anti- hexadiene at the same level of theory. Once run, the vibrational frequencies of the molecule were checked to be all positive and real, and the infrared spectrum was generated.

A note of the following energies were taken from the the output file:

• The sum of electronic and zero-point energies (-234.416255 a.u.)
• The sum of electronic and thermal energies (-234.408963 a.u.)
• The sum of electronic and thermal enthalpies (-234.408019 a.u.)
• The sum of electronic and thermal free energies (-234.447872 a.u.)

The summed zero-point energies and the summed thermal energies were used later to calculate the activation energies for the boat and chair transition states as opposed to the electrical energies of the structures, that do not take into account zero-point energy at 0 K or any additional translational, vibrational or rotational effects at higher temperatures.

Structure	Point Group	Energy/ Hartrees DFT/631G(d)	IR spectrum
	Ci	-234.61171166

Nf710 (talk) 23:13, 18 November 2015 (UTC) You have done the frequency claculation correctly and your theormochemistry is correct. But your havent compared the geometries of the two levels of theory.

Optimizing the "Chair" and "Boat" Transition States

The Chair

In the following section the transition structures for the Cope rearrangement in question were built and optimised using a variety of methods:

(i)Computing the force constants at the start of the calculation.

(ii)Using the redundant coordinate editor.

(iii)Using the QST2 method.

Following optimization the intrinsic reaction coordinate (IRC) was run. This allows a path of minimum energy to be followed from a transition state structure down to the local minimum of the potential energy surface .

The chair transition state was composed of 2 allyl fragments, that were first optimized individually using the HF/3-21G level of theory before making each transition state in GaussView. The terminal carbon atoms of the allyl fragments were set to be 2.2 Å apart and were arranged into a chair like orientation. This guess transition state was then optimized using 2 different methods, both of which using Hartree Fock and the 3-21G basis set. It is necessary to use alternative methods to a typical minimization when optimizing a transition state as the program needs to be aware of the direction of negative curvature. Such calculations can often be more computationally expensive than finding normal minima.

(i)The first method used was the TS (Berny) method; when optimizing using this method a good knowledge of the transition structure geometry is required. If the geometry is far from the true transition state geometry the optimization fails. The force constants in the this case were calculated once.

After the optimization had completed, one imaginary frequency at -818.81 cm^-1 was found, indicating a transition structure had been reached. An imaginary frequency is produced at a transition state as a result of the resultant force constant being negative. As the frequency of the motion is proportional to the square root of the force constant, an imaginary number is produced as a result.

Nf710 (talk) 23:50, 18 November 2015 (UTC) good understanding of how the second derivative of the PES (force constant) and quantum harmonic oscilator are linked!

Transition State	Structure	Energy/ Hartrees TS(Berny)	Point Group
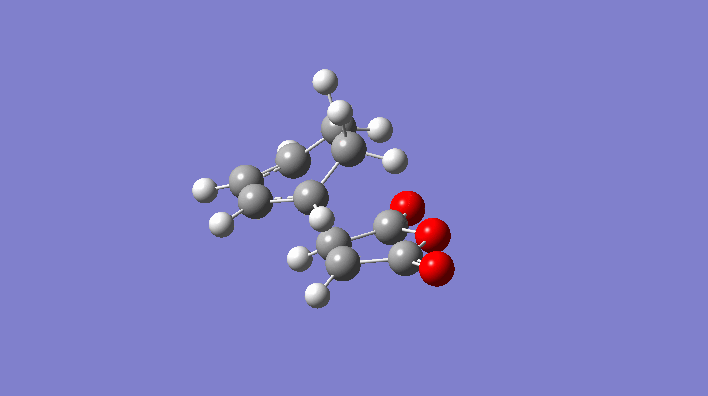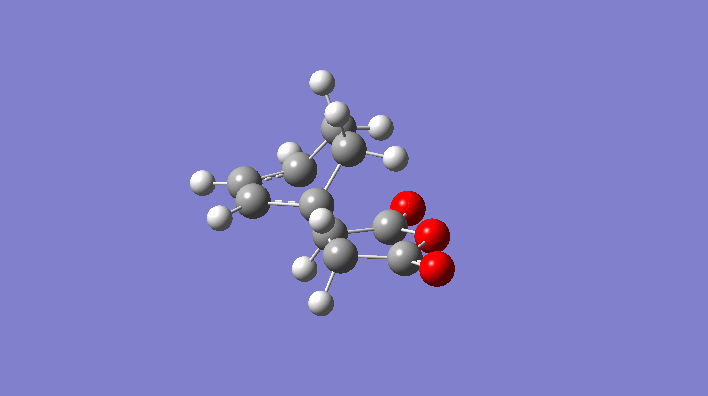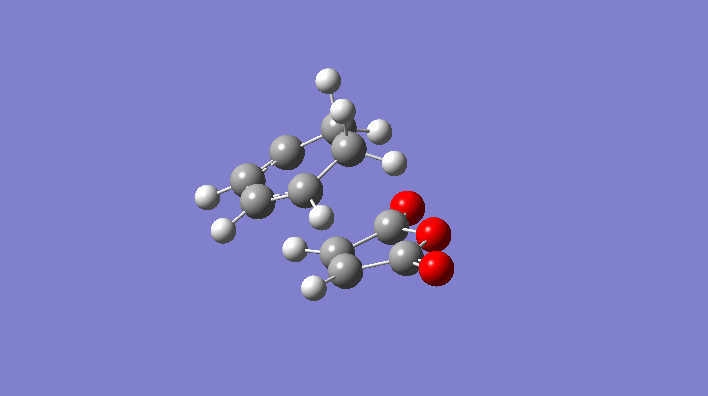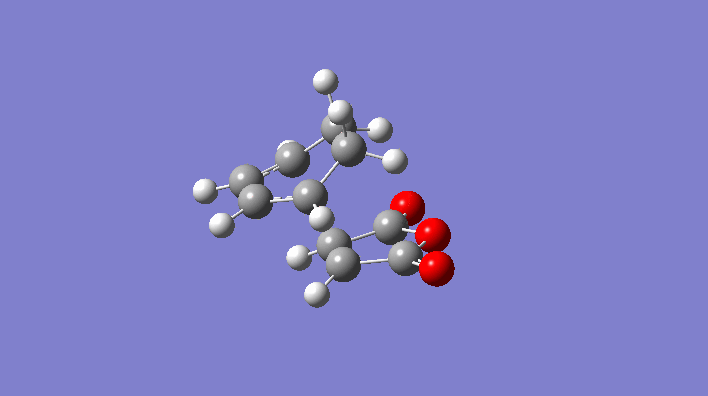
		-231.6172118	C2h

Nf710 (talk) 10:16, 19 November 2015 (UTC) Your chair energy looks to be a bit out here.

(ii) Secondly the frozen coordinate method was used; this method can be used before running a TS (Berny) calculation. This is a suitable choice when the predicted transition state structure is not close to the real structure. The redundant coordinator editor was used to freeze the terminal c-c bond distances to 2.2 Å for the first optimization. Once the rest of the molecule had been optimized to a minimum the distances were "unfrozen" and a TS (Berny) calculation was run in a similar fashion as above except the force constants in this case did not need to be recalculated.

Structure	Point Group	Energy/ Hartrees Frozen Coordinate	Transition State (Animation)
	C2h	-231.61521115

Comparatively the two methods provide very similar results. The first, although being quicker and less computationally expensive would not suffice in situations where the transition state geometry deviated far from reality. The resultant geometry of the two chair transition states was similar, both belonging to the C₂h point group. The bond forming/bond breaking lengths were 2.02047 Å after optimizing using the TS (Berny) alone and slightly longer after using the frozen coordinate method at 2.19939 Å.

The Boat

(iii) The boat transition structure was then optimized using the QST2 method. This method requires the input of the two minimum structures that lie either side of the transition state. The method then locates the transition structure that connects the reactants and products. Such a method can be useful if the structure of the transition state is not known precisely.

Two of the previously optimized "Anti2", Ci 1,5- hexadiene molecules were arranged and numbered in a specific order, as shown below, an optimization was then run. As can be seen the optimization failed, the structure produced was highly dissociated and clearly does not show the expected boat transition structure.

Starting Structure	Structure after Optimization

The optimization above failed as the QST2 method requires that the reactants and products be in a chemically realistic geometry.

A second optimization was then run, this time the dihedral angle was changed to 0° and the molecules were manipulated until the geometry below was reached. The optimization was run again. This time it converged to the transition structure and one imaginary frequency (-839.86 cm^-1) was produced.

Starting Structure	Transition Structure	Point group	Energy/ Hartrees QST2	Transition State (Animation)
		C2V	-231.60280239

It is not possible at this stage to decipher which of the conformers of 1,5- hexadiene corresponds to which transition state. It it however possible using an IRC to follow the minimum energy path of a transition structure down to its local minimum. It does so by travelling along the steepest part of the potential energy surface. Running an IRC can confirm that the transition state has been reached, and that it connects the reactants and products.

IRC Calculation

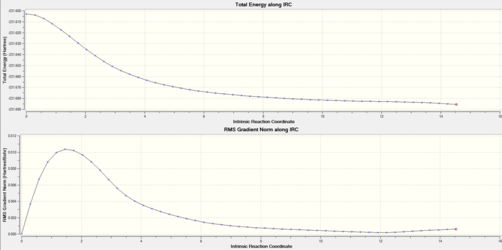
An IRC was conducted on the chair transition state structure previously optimized using the frozen coordinate method. The number of steps within an IRC calculation may be set; in this case an IRC was run in the forward direction due to the symmetrical nature of the reaction coordinate. The number of steps was set to 50.

IRC plot	Final Geometry after IRC Calculation

It can be seen from the plot that once the calculation had finished, the structure had not reached a minimum geometry. From the IRC you can see the energy plateau, however it had not reached a minimum. The final structure resembled the "gauche3" conformer, indicating that a minimum was nearly reached, this can also be seen from the plot. This suggests there were too few steps in the calculation. It can however be difficult to know the correct number of steps to use for an IRC calculation, if too many are used the coordinate may veer off and an alternative energy path may be followed. In order to obtain the minimum, a normal minimization was then run on the final IRC structure, using the Hartree Fock method and the 3-21G basis set. The final structure was that of the "gauche 3" conformer, and the energy was found to be -231.692239 a.u. This was similar to both of the "gauche2" and "gauche3" conformers of 1,5 -hexadiene energies, but geometrically it could be seen to resemble the "gauche3" conformer, belonging to the C1 point group.

Nf710 (talk) 23:58, 18 November 2015 (UTC)Good use of energies and conformation to deduce correct structure, your IRC looks a little strange like it over shot he minimum.

Activation Energies

Lastly the activation energies for the reaction via both transition states were calculated. Both transition structures were re-optimized using the DFT/ B3LYP/6-31G(d) level of theory. Frequency calculations were conducted on the structures previously optimized at the Hartree Fock 3-21G level.

Structure	Energy 3-21G/ Hartrees	Energy 6-31G(d)/ Hartrees	Energy + Zero Point Energy 3-21G/ Hartrees (at 0 K)	Sum of Electronic and Thermal Energies 3-21G (at 298.15 K)	Energy + Zero Point Energy 6-31G(d)/ Hartrees (at 0 K)	Sum of Electronicand Thermal Energies 6-31G(d) (at 298.15 K)	Point Group 3-21G , 631G(d)
"Anti2" conformer	-231.69253522	-234.61171166	-231.539611	-231.532567	-234.468755	-234.461963	Ci , Ci
Boat TS	-231.60280239	-234.54307876	-231.450924	-231.445294	-234.402360	-234.396016	C2v , C2v
Chair TS	-231.61721180	-234.55692628	-231.466701	-231.461341	-234.416255	-234.408999	C2v , C2v

The activation energies at 0 K were calculated by finding the difference between the and zero- point energies of the reactant and the transition states. The activation energies were also calculated at 298.15K, these are shown below in Kcal mol^-1.

	HF/ 3-21G at 0 K	B3LYP/ 6-31G(d) at 0 K	HF/ 3-21G at 298.15 K	B3LYP/ 6-31G(d) at 298.15 K	Experiment / Kcal mol-1at 0 K
ΔE (Chair) / Kcal mol-1	45.75	32.57	44.72	33.24	33.5 ± 0.5
ΔE (Boat) / Kcal mol-1	55.65	41.66	54.84	41.38	44.7 ± 2.0

Overall the results match the expected computed values reasonably well . It can be seen that the geometry remains similar for both basis sets; whilst the energies differ considerably. It is clear that either basis set is an adequate tool for examining the geometry of molecules; however when comparing energies the higher level of theory proves to be more accurate. It can be seen that the lower level of theory has produced a significant overestimation of the activation energy, whilst the higher level of theory has produced slightly underestimated results. This deviation from experimental results may reflect the approximations the program makes. In particular the computation of just one molecule introduces error, as inter-molecular forces are not taken into account. There are also calculations that may be run at a higher level of theory that would improve the accuracy of the results. It is too clear that accuracy of all of the results is also an outcome of the initial input guess geometry of the transition structures.

Nf710 (talk) 09:53, 19 November 2015 (UTC) good comparison of the energies and hypothesises of why the energy is not exact. You could have compared the geoms abit more but you have come to correct conclusion that a lower basis set still good at getting the geoms but not the energies. you could have compared the frequencies of the DFT molecules also.

Nf710 (talk) 09:53, 19 November 2015 (UTC) In general this is a good report. you have done most things asked of you, you showed good understanding of how transition states are found. however you could have shown more understanding of the theories used here.

The Diels-Alder Cycloaddition

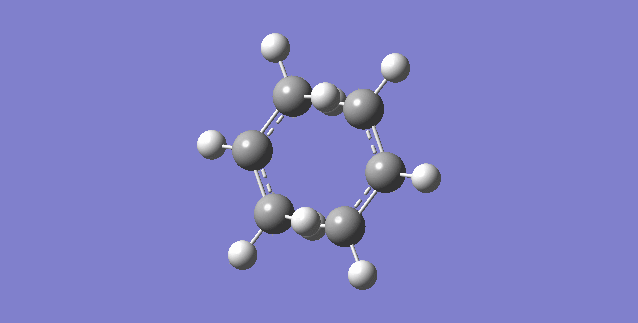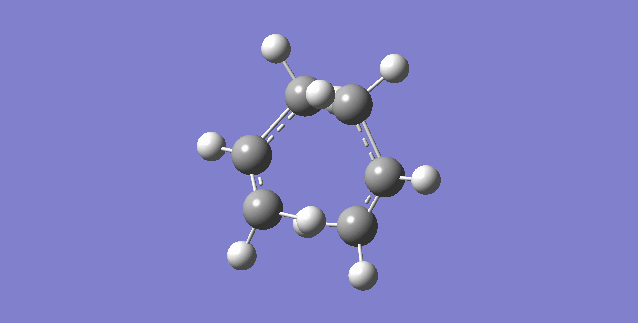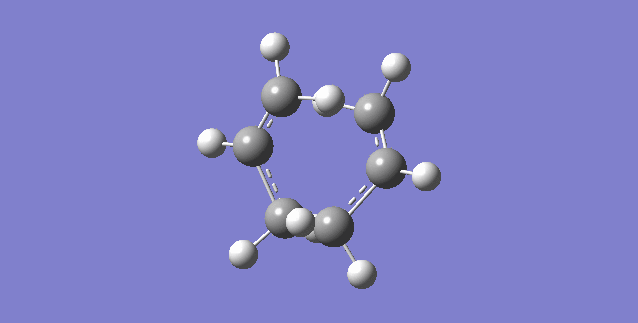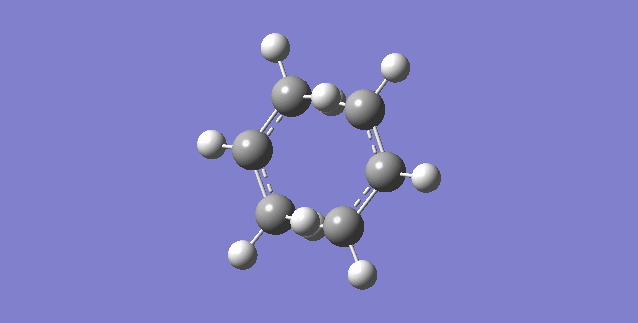
The following part of the experiment explored the Diels-Alder cycloaddition by investigating the transition state structures and analyzing the molecular orbitals. The Diels-Alder cycloaddition is a [4+2] pericyclic addition, in which two conjugated π systems add to form a ring. This occurs in a concerted fashion via a cyclic transition state. Heat is not necessarily required to drive the reaction as the formation of two new sigma bonds over the loss of two π bonds is favored, however heat is often used to drive the reaction. The prototypical example of ethene (the dienophile) and cis-butadiene (the diene) is shown below.

Diels-Alder cycloadditons may be termed normal electron demand additions, in which the diene is electron rich and the dienophile is electron deficient; or as inverse electron demand additions if the reverse is the case. The electronic properties dictate the interactions between the HOMO's and LUMO's of a given reaction. For an allowed reaction the HOMO of one of the reactants must interact with the LUMO of the other. In more complex cases in which the reactants carry substituents, secondary orbital effects are possible. These topics were explored during the experiment.

Prototypical Reaction

Firstly the HOMO and LUMO of cis-butadiene was visualized after optimization using the AM1 semi-empirical molecular orbital method. The HOMO is anti-symmetric with respect to the plane of symmetry through the molecule, and the LUMO is anti-symmetric.

Cis-butadiene LUMO	Cis-butadiene HOMO

Next an approximate transition structure was built using the optimized cis-butadiene and an optimized ethene molecule. The transition state structure was drawn so as to maximize the orbital overlap between the HOMO of cis-butadiene and the LUMO of ethene. The inter-fragment distances were set to be 2.2 Å and the point group to Cs. The structure was then optimized using the TS (Berny) method and the 3-21G basis set. This method was selected as for the prototypical reaction it was not necessary to use the frozen coordinate method, since the transition state geometry was a reasonably close guess. The calculation completed producing one imaginary frequency was obtained at -818.31 cm^-1, indicating a transition state was reached. The point group was Cs. Afterwards an IRC calculation was also run in both directions, to check that the singular transition state had been located, the plot is shown below.

(A bit pedantic here: you've mentioned that you're using AM1, but now saying you're using a 3-21G basis set. Many methods use 3-21G but from your results I can see you used HF, so it's best to explicitly state HF/3-21G Tam10 (talk) 18:18, 10 November 2015 (UTC))

Structure	IRC Plot	Transition Structure

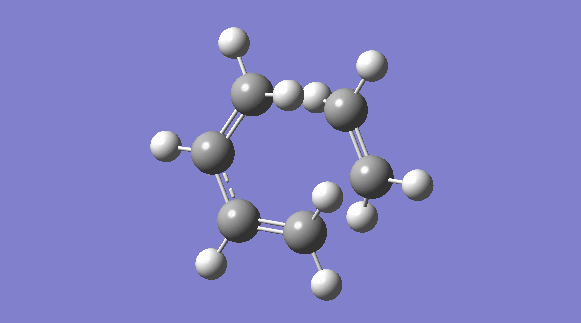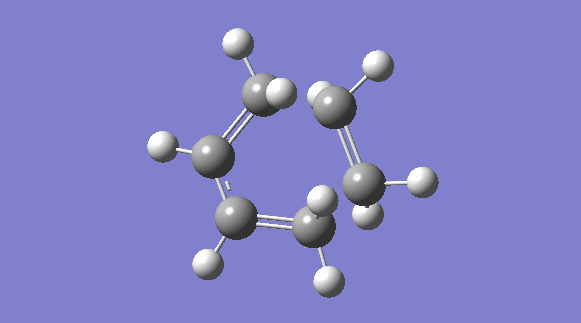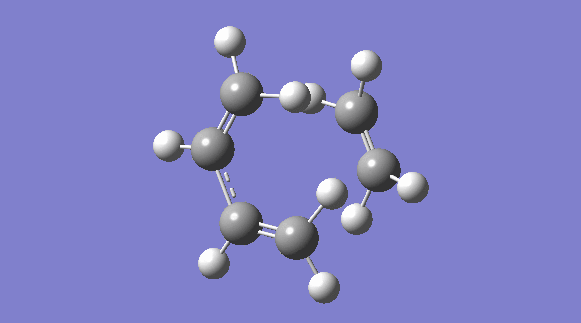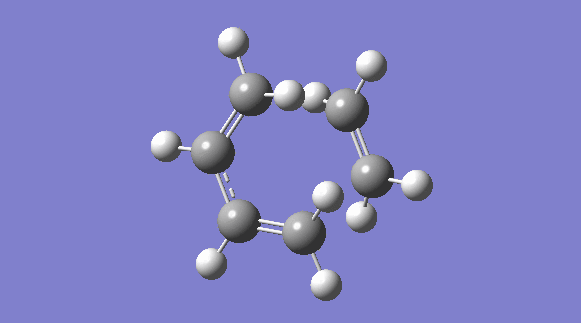
The imaginary frequency representing the transition state, shown above, indicates that the reaction proceeds in a concerted fashion, where the bonds are made and broken synchronously.The partly formed c-c bond lengths were 2.20940 Å and 2.20975. The partially formed bonds are less than the sum of the carbon Van der Waals' radii and therefore indicate a definite bonding interaction. The other c-c bond lengths lied in between the typical sp³- sp³ bond lengths and sp²-sp³ bond lengths, this is due to the conjugated, aromatic nature of the transition state.

The lowest positive frequency is shown below. Conversely here bond formation is not favoured, and seems to be happening in an asynchronous fashion.

(You almost fell into the trap here, but recovered. Be careful using the word "asynchronous", which, in this context, refers to one bond being formed after another Tam10 (talk) 18:18, 10 November 2015 (UTC))

The HOMO and LUMO of the transition structure was then evaluated. The symmetrical LUMO and the anti-symmetrical HOMO are shown below.

Anti-symmetrical HOMO	Symmetrical LUMO

It can be seen that the LUMO of the electron deficient ethene interacts with the HOMO of the butadiene to form the the HOMO above. This is the case for normal electron demand additions; as the energy gap between the LUMO of the diene and the HOMO of the dienophile is smaller than the converse gap between the LUMO of the dieneophile and the HOMO of the diene. Despite the fact that this reaction is allowed, it is a poor reaction, resulting in poor yields experimentally, due to the absence of substituents on the fragments.

(Include the MOs for ethene to help explain this to the reader Tam10 (talk) 18:18, 10 November 2015 (UTC))

(It would be good to expand on this last statement. You have pointed out that an electronically allowed reaction doesn't necessarily mean the reaction will happen quickly Tam10 (talk) 18:18, 10 November 2015 (UTC))

Maleic anhydride and Cyclohexa-1,3-diene Diels-Alder

(A little confused. It seems like all of these are exo? Tam10 (talk) 18:18, 10 November 2015 (UTC))

The selectivity of the Diels-Alder reaction was then studied by evaluating the 2 possible transition states (endo and exo) that are possible in the reaction between maleic anhydride and cyclohexa-1,3-diene. The kinetically controlled reaction proceeds primarily via the endo transition state to give the kinetically favored endo diasteroisomer (this preference is also referred to as the endo rule). The two products can be seen below.(SOURCE 6)

Firstly a maleic anhydride and a cyclohexa-1,3-diene molecule were optimized individually before making the transition structures. The endo guess transition structure was built first in GaussView, so that the π orbitals belonging to the carbonyl groups of the maleic anhydride were lying directly underneath the π orbitals of the cyclohexa-1,3-diene. The partial bonds between two fragments were set to be 2.2 Å again and the point group to Cs. Secondly optimizations were run, using two different basis sets for comparison: The Hartree Fock/ 3-21G level of theory and the AM1 semi-empirical molecular orbital method. In both cases an initial optimization was run using the frozen coordinate method, as it was likely that the transition structures were too dissimilar from reality to run a TS (Berny) calculation first. For both transition structures the partial c-c sp³ - sp³ bond lengths were frozen to 2.2 Å and optimized, the bonds were then "unfrozen" as before and re-optimized using the TS (Berny) method. The point group remained Cs. One imaginary frequency was found at -605.60 cm^-1; the corresponding frequency is shown below.

Hartree Fock Method

Endo Structure	Transition State	Energy/ Hartrees HF/3-21G	HOMO	LUMO
		-605.64958804

It can be seen that the LUMO is symmetrical with respect to the plane of symmetry, and the HOMO anti-symmetrical, with a nodal plane through the centre of the structure. From this it can be seen that there is bonding interaction between the carbonyl π orbitals of the anhydride and the newly forming π orbital at the back of the diene. These secondary orbital interactions result in a stabilised transition state, these are only possible due to how the anhydride was arranged to be directly underneath the diene. The transition state animation also shows the synchronicity of the bond formation.

Next the exo transition structure was made, this time ensuring the that the carbonyl groups of the anyhydride were pointing away from the the diene π bonds. The treatment was applied as above. Again the point group was Cs and an imaginary frequency was found at -647.53 cm^-1.

Exo Structure	Transition State	Energy/ Hartrees HF/3-21G	HOMO	LUMO
		-605.60359125

Similarly here the bond forming is synchronous and facile. Both the HOMO and LUMO are anti-symmetrical with respect to the plane. Here the secondary orbital effects observed above are absent. Resulting in the exo transition state being less stable; however despite the stabilised bonding interaction of the endo product above, it should be noticed that there is not a large difference between the energies of the two.

(This isn't really enough. You should calculate the activation energies using the reactant energies and compare them (for example, in KJ/mol or Kcal/mol) to see which is the kinetically preferred structure Tam10 (talk) 18:18, 10 November 2015 (UTC))

AM1 Semi-empirical Molecular Orbital Method

The same process as above was followed, however this time using the semi-empirical method. The results are summarized below. Single imaginary frequencies were found for the endo and exo transition states, they were 806.99 cm^-1 and -810.88 cm^-1 respectively. The point groups for both were as before Cs.

Structure	Transition State	Energy / Hartrees Semi-empirical AM1	HOMO	LUMO
EXO		-0.05042001
ENDO		-0.05119821

By comparison of the two methods,it is again clear that using different methods and basis sets does not have a great effect on the outcome of the geometry, but does however with regards to the energy. The AM1 method was much quicker to run, suggesting it may be a less computationally expensive method.

A sketch was produced of both transition structures (AM1 method), and the bond lengths compared. By looking at the extent of bonding in each it is possible to evaluate the bonding interactions between the molecules further.

Exo sketch	C10-C2 / Å	C14 -15 / Å	C10-C15 / Å	C13-C14 / Å
	2.26065	1.39758	1.37003	1.37003

Endo sketch	C4 - C16/ Å	C4 - C5 / Å	C5-C6/ Å	C6-C1 / Å
	2.17057	1.39436	1.39679	1.39436

The majority of bond lengths in the table are in between that of a single sp³–sp³ c-c bond length (1.52 Å) and the sp³–sp² c-c bond length (~134 Å for multiple bonds), these bond lengths correspond to the double bonds that are either being broken or formed during the reaction and are this length due to the aromatic character of the transition state, as mentioned above. The endo transition state is more stable, as a result of this there is more bonding character between the two fragments. This information does also show that the endo structure is infact more strained and sterically hindered, however the secondary orbital effects result in a stabilizing reaction that overrides sterics in this case. This reaction again is normal electron demand. The anhydride LUMO is lower in energy than that of ethene due to the electron withdrawing substituents, similarly the diene is more electron rich as a result of the electron donating alkyl substituents. Therefore this reaction is allowed and more facile than the example above.

Conclusion

Overall the experiment showed the wealth of information that could be elucidated about reaction mechanisms and in particular transition states by computational means. Many methods and basis sets were used throughout the experiment; it was found that when interested in geometry any of the basis sets used would suffice as they produced similar answers, however when looking t energies the results were markedly different. The 6-31G(d) level of theory provided activation energies that were in good agreement with experiment, more so than the lower level of theory. The program was also used to visualise molecular orbitals and look at bonding interactions of the transition states,enabling the comparison of sterics and bonding interactions. This proved to be significant when looking at the preference of the endo disateroisomer formation.The reaction was found to go via a concerted mechanism in this study, however some ab initio studies have led to opposite conclusions according to literature, some finding that the mechanism goes via a two-step or asynchronous mechanism. For the methods used above however the conclusion reached agrees with literature.