Leena Rantala: Module 3

The Cope Rearrangement

The Cope rearrangement is an organic reaction named after Artur C. Cope who was the first to report it^[1] It involves a [3,3]-sigmatropic rearrangement of 1,5-dienes. The reaction is pericyclic, meaning all bonds are broken and formed in a concerted manner^[2]. The aim of this report is to use molecular orbital-based computational methods to investigate the different conformers of 1,5-hexadiene and to model the transition state of the rearrangement.

Optimising the reactants and products

The Hartree-Fock method and 3-21G basis set are used for the initial optimisation of the different conformers. The HF method is simple and the 3-21G basis set is a low level basis set, but they are accurate enough to provide a good starting point for further optimisation as they are relatively quick and have low computational cost. The higher level DFT/B3LYP method and 6-31G* basis set are more complex and are used for further optimisation of the lowest energy conformers.

HF method and 3-21G basis set

The optimised structures are shown below along with their corresponding energies and symmetries.

Table 1: The HF/3-21G optimised structures and energies of the different 1,5-hexadiene conformers.

Conformer	Structure	Point Group	Energy (a.u.) HF/3-21G	Relative Energy (kcal/mol)	.log file
Gauche 1		C₂	-231.69153	0.71	Gauche 1
Gauche 2		C₂	-231.69167	0.62	Gauche 2
Gauche 3		C₁	-231.69266	0.00	Gauche 3
Gauche 4		C₂	-231.68772	3.10	Gauche 4
Gauche 5		C₁	-231.68962	1.91	Gauche 5
Gauche 6		C₁	-231.68916	2.20	Gauche 6
Anti 1		C₂	-231.69260	0.04	Anti 1
Anti 2		C_i	-231.69254	0.08	Anti 2
Anti 3		C_2h	-231.68907	2.25	Anti 3
Anti 4		C₁	-231.69097	1.06	Anti 4

File:Butane conformers.svg

Figure 2: The variation of relative energy with dihedral angle in butane. Taken from the 'alkane stereochemistry' article in Wikipedia.

When considering the variation in relative energy of conformer with the dihedral angle (butane is a classic example, see Figure 2), two types of conformations are generally minima: antiperiplanar and gauche. The antiperiplanar conformations (shortened to anti in discussion and tables) are the lowest energy conformers due to their favourable alignment of atoms, minimising steric clashes of terminal groups and allowing hyperconjugation. Gauche conformers are only slightly higher in energy, as although they suffer from increased steric repulsion, the close alignment of these groups results in increased Van der Waals interactions between them, lowering the energy.^[3]

The results in Table 1 above show that according to our calculation, the Gauche 3 conformer is the most stable, although the Anti 1 and Anti 2 conformers showed only a small difference in energy. This does not agree with expectations and may be due to the primitive nature of the HF/3-21G method and basis set. Further optimisation at a higher level of accuracy was carried out on these three conformers to confirm their relative stability.

The DFT/B3LYP method and 6-31G* basis set

The three lowest energy conformers - Gauche 3, Anti 1 and Anti 2 - were further optimised. The real output files for each of the three conformers were checked and they had all converged.

Table 2: The B3LYP/6-31G optimised structures and energies of the three most stable conformers.

Point group	Energy (a.u.)	Relative energy (kcal mol^-1)	.log file
C₂	-234.61133	0.29	Gauche 3
C_i	-234.61180	0.00	Anti 1
C₁	-234.61170	0.06	Anti 2

The optimised structures are very similar to those obtained with the HF/3-21G method, with respect to dihedral angles and bond lengths. All conformers showed a lower total electronic energy compared to that obtained with HF/3-21G (albeit direct comparison is impossible between two distinct methods), but the relative ordering of the conformers is different. The Anti conformers were both more stable than the Gauche 3 conformer, as is predicted. As the molecule is a diene, the increased stability of the Anti conformers may also be attributed to the possibility of hyperconjugation due to ideal alignment of molecular orbitals.

These results show that HF/3-21G is relatively good at providing optimised structures, but perhaps fails to take into account all contributions to the total energy of the system. The B3LYP/6-31G method and basis set is indeed more accurate, as it succeeded in predicting the correct energy order.

Frequency analysis

A frequency analysis was run on the three conformers with the same method and basis set. No imaginary frequencies were observed, confirming that the structures were indeed minima. The input files for the frequency analysis were manually edited for another frequency analysis at 0 K and 1 atm.

All thermochemistry results are shown below in Table 3.

Table 3: Thermochemistry results for the three most stable conformers at 298.15 K and 0 K.

Temperature (K)	0	298.15			0
	Sum of electronic and zero-point energies (a.u.)	Sum of electronic and thermal energies at (a.u.)	Sum of electronic and thermal enthalpies at (a.u.)	Sum of electronic and thermal free energies at (a.u.)	Sum of electronic and zero-point energies (a.u.)	Sum of electronic and thermal energies at (a.u.)	Sum of electronic and thermal enthalpies at (a.u.)	Sum of electronic and thermal free energies at (a.u.)
Gauche 3	-234.46869	-234.46146	-234.46052	-234.50011	-234.46869	-234.46869	-234.46869	-234.46869
Anti 1	-234.46929	-234.46197	-234.46102	-234.50016	-234.46929	-234.46929	-234.46929	-234.46920
Anti 2	-234.46921	-234.46186	-234.46091	-234.50082	-234.46669	-234.46669	-234.46669	-234.46669

We see that at 0 K, the sum of electronic and zero-point energies is the same as the sum of electronic and thermal energies, the sum of electronic and thermal enthalpies and the sum of electronic and thermal free energies. This is as expected, as at zero-point temperature the molecule should only have zero-point energy.

Optimising the Chair and Boat Conformers

The HF method and 3-21G basis set were used to optimise the CH₂CHCH₂ allyl fragment, which was then used to construct the 'boat' and 'chair' transition state structures.

Chair Conformer

Berny Transition State Optimisation

The chair conformer was optimised to a Berny transition state using HF/3-21G (.log file). One imaginary frequency was observed at -818 cm^-1 (animation). This corresponds to the elongation/contraction of the bonds being broken/formed during the Cope rearrangement. These bond lengths were 2.02 Å.

Frozen Coordinates

Using the Redundant Coordinate Editor, the key bond lengths were set to 2.20 Å and the structure optimised to a minimum. The structure was then further optimised to a Berny transition state (.log file). The optimised bond lengths for the forming bonds were 2.02 Å, i.e. identical to those obtained from the first Berny transition state optimisation. Looking at the optimised structure, it is nearly impossible to tell which conformers of 1,5-hexadiene it arises from. In order to investigate this, the Intrinsic Reaction Coordinate method is used in the following section.

IRC Method

The HF/3-21G optimised structure of the chair transition state was optimised with the IRC method and 50 points on the HPC server (D-space link:http://hdl.handle.net/10042/to-11228).

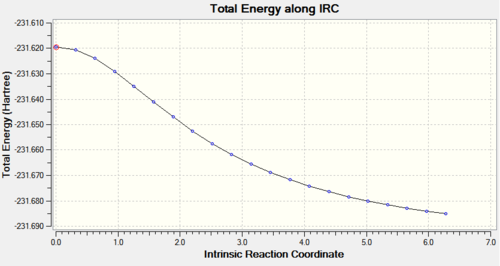
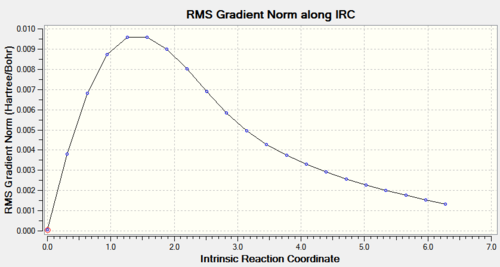
The calculation had not reached a minimum in the 21 steps it calculated, so it was repeated with force constants computed at every step (D-space link:http://hdl.handle.net/10042/to-11285). This time the calculation converged in 47 steps.

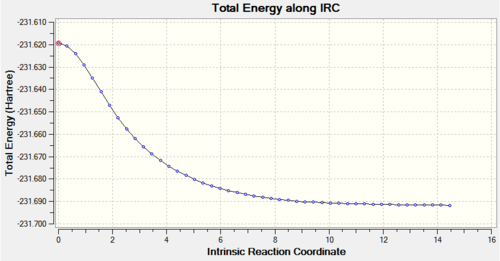
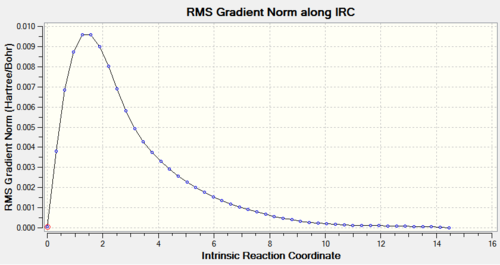
Boat Conformer

QST2 Method

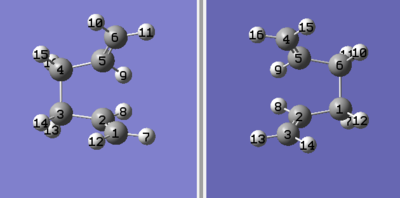
The Anti 2 molecule from the first part was used to 'draw' structures for the reactant and product, and the numbering of the atoms was altered to give the following:


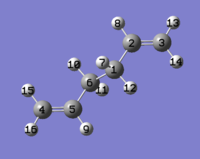
Figure 6: The numbering of the reactant (left) and product (right) used in the QST2 optimisation.

Initial optimisation using the QST2 method failed as it was unable to consider rotation about the central bonds (.log file). The starting structures are too far from the optimised structures for the QST2 method to locate the minima, so they must be altered.

The structures of the reactant and product were altered by setting the C2-C3-C4-C5 dihedral angle as 0° and the C2-C3-C4 and C3-C4-C4 bond angles to 100° (see below).

The optimisation was run again (.log file) and the real output file checked to see the calculations had converged. One imaginary frequency was predicted at -840 cm^-1, corresponding to the Cope rearrangement (animation). The optimised structure is shown below.

Intrinsic Coordinate Reaction (IRC) Method

The QST2 optimised boat transition state structure was further optimised with the IRC method and 50 points on the HPC server (D-space link: http://hdl.handle.net/10042/to-11289). The calculation converged in 47 steps.

Activation Energies

The HT/3-21G optimised structures were further optimised using the DFT method and B3LYP/6-31G* basis set (chair .log file boat .log file). Frequency analysis was carried out to get the thermochemistry results. The chair and boat conformers both showed one imaginary frequency at -566 cm^-1 and -531 cm^-1 respectively, the vibration corresponding to the Cope rearrangement.

The geometries of the transition state structures obtained at the two different levels of theory (HF/3-21G and B3LYP/6-31G*) are very similar. However, both transition states and the reactant (Anti 2) had lower energies as a result of the optimisation at a higher level (again, direct comparison is impossible between different methods). With HF/3-21G, the chair is 10.37 kcal mol^-1 lower in energy, and with B3LYP/6-31G*, it is 8.72 kcal mol^-1 lower. This corresponds with expectations.

Table 4: Thermochemistry results from the two levels of theory for the chair and boat conformers.

Method/basis set	HF/3-21G			B3LYP/6-31G*
Thermochemistry	Electronic energy (a.u.)	Sum of electronic and zero-point energies (a.u.)	Sum of electronic and thermal energies (a.u.)	Electronic energy (a.u.)	Sum of electronic and zero-point energies (a.u.)	Sum of electronic and thermal energies (a.u.)
Chair TS	-231.61932	-231.46670	-231.46134	-234.55698	-234.41493	-234.40901
Boat TS	-231.60280	-231.45093	-231.44530	-234.54309	-234.40234	-234.39601
Anti 2	-231.69254	-231.53954	-231.53257	-234.61170	-234.46921	-234.46186

Activation energies were calculated as the difference between the sum of electronic and thermal energies of the reactant (Anti 2) and the product (chair or boat TS), based on the results obtained at both levels of theory.

Table 5: Calculated activation energies for the chair and boat conformers.

Method/basis set	HF/3-21G		B3LYP/6-31G*		Literature^[4]
Temperature	0 K	298.15 K	0 K	298.15 K	0 K
ΔE_Chair (kcal mol^-1)	45.71	44.70	34.06	33.16	33.5 ± 0.5
ΔE_Boat (kcal mol^-1)	55.60	54.76	41.96	41.32	44.7 ± 2.0

With both levels of theory, the activation energies are lower for the chair transition state. For the chair conformer, the B3LYP/6-31G* level of theory gives a result that is very close to (and within error of) the experimental result previously reported in literature. Similarly for the boat, the higher level of theory result has better agreement with literature, but the difference is slightly larger than that of the chair.

Conclusion

The different conformers were successfully optimised and modeled using two levels of theory: HF/3-21G and B3LYP/6-31G*. Both gave very similar structures, but the higher level B3LYP/6-31G* method and basis set proved more accurate in predicting the relative stability of the lowest energy Gauche and Anti conformers. Thermochemical data was studied to compare the activation energies, which again showed the greater accuracy of B3LYP/6-31G* as it produced results that agreed better with literature.

The Diels-Alder Cycloaddition

The Diels-Alder reaction is an ideal example of a [π_4s+π_2s] cycloaddition reaction between a diene and a dienophile. It was first reported by Otto Diels and Kurt Alder in 1928. In this report the transition state of the D-A reaction between cis-butadiene and ethene is studied to investigate the molecular orbitals and gain a better understanding of the reaction mechanism.

Consequently, the reaction between 1,3-cyclohexadiene and maleic anhydride is investigated. As the dienophile (maleic anhydride) is substituted, the reaction has two possible outcomes: an endo- and exo-product, depending on the alignment of the reactants. The endo-product generally predominates. By exploring the transition states, their energies and secondary orbital interactions, we can determine the kinetic and thermodynamic product of the reaction, and thus explain the selectivity.

Reactant Optimisation

Cis-butadiene was optimised with the semi-empirical AM1 method, and the real output file checked to see the files had converged (Diene .log file and ethene .log file).

The HOMO and LUMO were visualised for both cis-butadiene and ethene. The cis-butadiene LUMO and the ethene HOMO were both deemed symmetric as they have a plane of reflection (in the images below it is vertical and perpendicular to the plane of the page). The cis-butadiene HOMO and ethene LUMO were both antisymmetric, without planes of reflection.

Cis-butadiene HOMO	Cis-butadiene LUMO	Ethene HOMO	Ethene LUMO

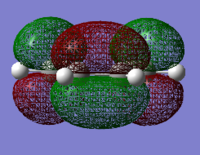Antisymmetric	Symmetric	Symmetric	Antisymmetric

Transition State Optimisation

The optimised cis-butadiene and ethene fragments were combined and oriented in a manner reflecting the possible structure of the transition state. Bond breaking/forming distances were set to 2.2 Å by freezing the coordinates and the structure optimised to a minimum using the AM1 method (.log file). The bonds were then derived and the structure optimised to a Berny transition state with the same method (.log file). The angle of approach of ethene isn't directly from above, but 99.4°. The bond length of the partially formed σ C-C bonds was 2.12 Å.

The double C-C bond length in the optimised structure of cis-butadiene is 1.38 Å and the single C-C bond is 1.40 Å. Typical sp³ and sp² C-C bonds are 1.53 Å and 1.32 Å respectively^[5]. The similarity lengths of single and double bonds in the optimised structure suggests they are also similar in nature; the double bonds are in fact becoming more like single bonds and the single bond is gaining double bond character (due to movement of π-electrons around the system, from a double bond to form a new σ C-C bond or the new п-bond).

The length of the partially formed bonds at 2.12 Å is much longer than a single bond, so it is not yet fully bonding in the optimised transition state.

One imaginary frequency was observed at -956 cm^-1. This corresponds to the formation of the new σ C-C bonds, and is a synchronous process. The distance between the terminal carbons of cis-butadiene and ethene shortens, showing the bond formation. In addition, the double C-C bond distances in cis-butadiene and ethene are seen to elongate, and the single C-C bond in cis-butadiene shortens, representing the changes in bond character (from double to single and single to double).

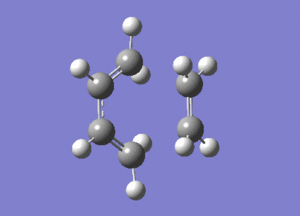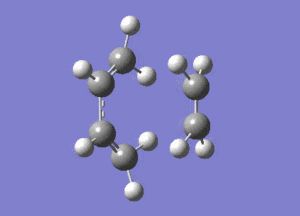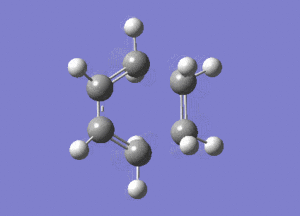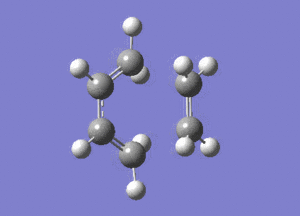
The lowest positive frequency occurs at 147 cm^-1. This corresponds to an asynchronous twisting of the ethene fragment planar to the cis-butadiene. If this were to correspond to the transition state bond formation/breakage, the reaction would not be concerted.

The HOMO and LUMO have been visualised below. We see that the transition state's antisymmetric HOMO is a combination of cis-butadiene's antisymmetric HOMO and ethene's antisymmetric LUMO. There is preservation of symmetry, suggesting the reaction is allowed.

HOMO (AM1)	LUMO (AM1)

Antisymmetric	Symmetric

A Study of the Regioselectivity

NOTE: At 7 pm on Thursday I noticed I had in fact the wrong structure for maleic anhydride (I had replaced the C-O-C with a C-CH₂-C). The following work is what I did with the incorrect structure (up to about 7 pm on Thursday).

Reactant Optimisation

1,3-cyclohexadiene and maleic anhydride were optimised separately using the semi-empirical AM1 method. Frequency analysis showed no imaginary frequencies, confirming the structures were minima.

1,3-cyclohexadiene	maleic anhydride

1,3-cyclohexadiene HOMO	1,3-cyclohexadiene LUMO	maleic anhydride HOMO	maleic anhydride LUMO

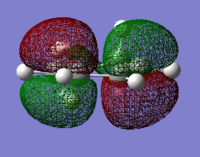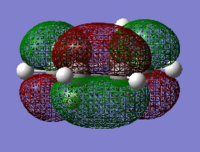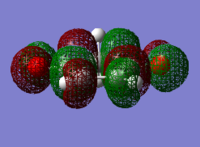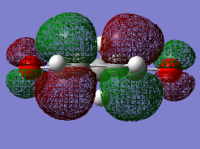
Optimisation of the Transition State

The optimised diene and dienophile fragments were combined and first optimised to a minimum with the distance between the terminal carbons involved in the bond formation set to 2.20 Å. The resulting exo- and endo-structures were then optimised to a Berny transition state.

The resulting exo-transition state structure showed one imaginary frequency at -835 cm^-1. The endo-transition state structure showed one imaginary frequency at -826 cm^-1. Both imaginary vibrations represented the formation of the new σ C-C bonds.

	Exo-product	Endo-product
Structure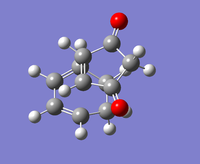
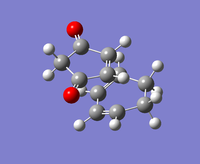
Jmol
Relative energy (kcal mol^-1)	1.05 (5.760990008604)	0.00 (4.70826106501)

Compound	HOMO		LUMO
exo-product
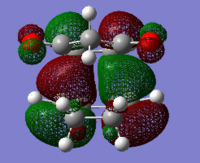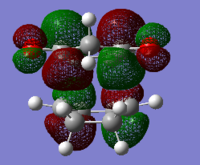
endo-product

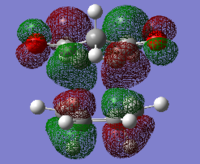
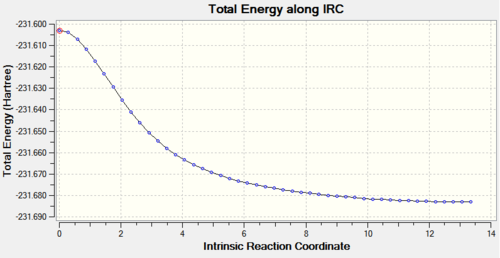
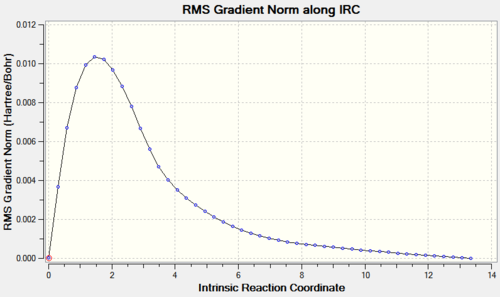
IRC Study

Both endo and exo products were further optimised with the IRC method on the HPC server, with 100 points, following the IRC in both directions and calculation force costants always (D-space links: Exo and Endo). The results have been summarised below.

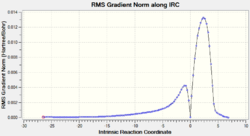
Compound	TS structure	C-C bond forming length (Å)	RMS vs IRC	Total energy vs IRC
		2.15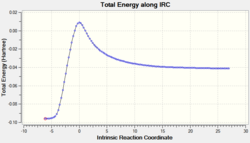
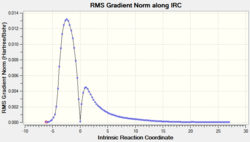
		2.15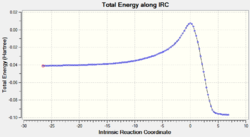

The relative energies of the reactants (1,3-cyclohexadiene and maleic anhydride), transition states, and products were determined from the graphs of total energy vs IRC.

Product	Reactants (kcal mol^-1)	TS (kcal mol^-1)	Product (kcal mol^-1)
Exo	-25.87 (0.00)	5.76 (1.05)	-60.14 (0.53)
Endo	-25.80 (0.07)	4.71 (0.00)	-60.67 (0.00)

From the graphs of total energy vs IRC and the relative energies listed in the table above, we see that the reactants for the exo-reaction are initially lower in energy, but the exo-transition state and product are higher in energy. As the endo-mechanism has both the lower energy transition state and product, it is both the kinetic and thermodynamic product.

A Study of the Regioselectivity (CORRECTED)

NOTE: At 7 pm on Thursday I noticed I had in fact the wrong structure for maleic anhydride (I had replaced the C-O-C with a C-CH₂-C). This the work I had time to complete with the corrected structure.

Reactant Optimisation (CORRECTED)

1,3-cyclohexadiene and maleic anhydride were optimised separately using the semi-empirical AM1 method and convergence checked (1,2-cyclohexadiene .log file and maleic anhydride .log file). Frequency analysis showed no imaginary frequencies, confirming the structures were minima. The optimised structures and jmols are shown below.

1,3-cyclohexadiene	maleic anhydride

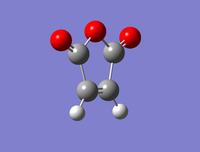
The HOMO and LUMO were visualised for both reactant molecules. The 1,3-cyclohexadiene LUMO and maleic anhydride HOMO were deemed symmetric as they have a plane of reflection (in the images below it is vertical and perpendicular to the plane of the page).

1,3-cyclohexadiene HOMO	1,3-cyclohexadiene LUMO	maleic anhydride HOMO	maleic anhydride LUMO

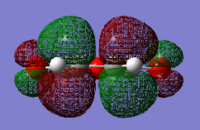
Antisymmetric	Symmetric	Symmetric	Antisymmetric

Optimisation of the Transition State (CORRECTED)

The optimised diene and dienophile fragments were combined and first optimised to a minimum with the distance between the terminal carbons involved in the bond formation set to 2.20 Å. The resulting exo- and endo-structures were then optimised to a Berny transition state. The forming bond lengths came out as 2.17 Å for both products.

The resulting exo-transition state structure showed one imaginary frequency at -813 cm^-1 (animation). The endo-transition state structure showed one imaginary frequency at -807 cm^-1 (animation). Both imaginary vibrations represented the formation of the new σ C-C bonds.

Table 6: Optimised structures and relative energies of the exo- and endo-transition states.

	Exo-product	Endo-product
Structure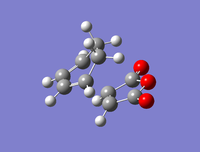
Jmol
Relative energy (kcal mol^-1)	0.68	0.00
.log files	minimum Berny TS	minimum Berny TS

The HOMO's and LUMO's for both exo and endo structures were visualised and have been tabulated below (there are two pictures for each MO from different angles). All the visualised HOMO's and LUMO's are antisymmetric. From the images we see that the HOMO for both transition state structures is a combination of the antisymmetric HOMO of 1,3-cyclohexadiene and the antisymmetric LUMO of maleic anhydride (as a reaction is only allowed when molecular orbitals of the same symmetry or antisymmetry combine, and there is preservation of symmetry).

The symmetric LUMO+1's show secondary orbital interactions between the π_C=O orbital of maleic anhydride and the π_C=C of 1,3-cyclohexadiene. The HOMO and LUMO show significant nodes around the oxygens, pushing electron density into the ring system and aiding the secondary orbital interactions^[6].

Table 7: Visualisation of the HOMO's and LUMO's of the exo- and endo-transition states.

	HOMO		LUMO		LUMO+1
exo-product
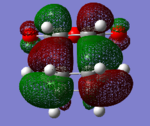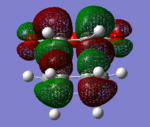endo-product

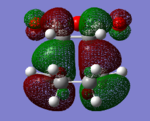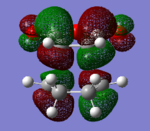IRC Study (CORRECTED)

Both endo and exo products were further optimised with the IRC method on the HPC server, with 100 points, following the IRC in both directions and calculation force costants always (D-space links: Exo and Endo). The results have been summarised below.

Table 8: Results from the IRC optimisation of the exo- and endo-transition states.

Compound	TS structure	C-C bond forming length (Å)	RMS vs IRC	Total energy vs IRC
		2.17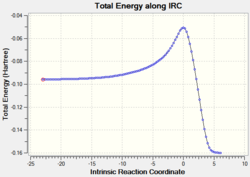
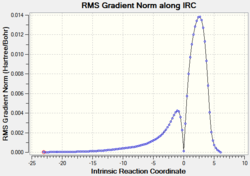
		2.16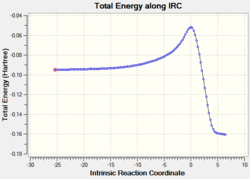

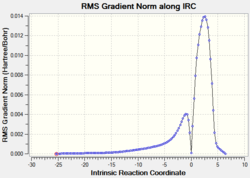
The relative energies of the reactants (1,3-cyclohexadiene and maleic anhydride), transition states, and products were determined from the graphs of total energy vs IRC.

Table 9: Activation energy and relative energies of the exo and endo reactants, transition states and products. Total energies and shown in brackets.

Product	Reactants (kcal mol^-1)	Transition State (kcal mol^-1)	Product (kcal mol^-1)	Activation energy (kcal mol^-1)
Exo	0.00 (-60.11)	0.68 (-31.64)	0.17 (-100.34)	28.47
Endo	0.67 (-59.44)	0.00 (-32.32)	0.00 (-100.51)	27.12

From the graphs of total energy vs IRC and the relative energies listed in the table above, we see that the reactants for the exo-reaction are initially lower in energy, but the exo-transition state and product are higher in energy. The endo-product shows a lower activation energy by 1.35 kcal mol^-1.

Conclusion

The semi-empirical AM1 method was used to model the transition states of both exo- and endo-products for the reaction between 1,3-cyclohexadiene and maleic anhydride. The Intrinsic Reaction Coordinate method was also used to examine the variation in energy and RMS gradient with reaction coordinate. The endo-transition state was shown to be lower in energy, resulting in a lower activation energy. The endo-product was also lower in energy, making it both the kinetic and thermodynamic product of the reaction, explaining its dominance.

The symmetry of MO's was determined and reactions identified as allowed. Analysis of MO's also showed secondary orbital interactions, aiding the stabilisation of transition states.

It would be interesting to carry out these calculations on a higher level of theory (for example B3LYP/6-31G*), although AM1 proved to be quite reliable.

↑ A. C. Cope, E. M. Hardy, J. Am. Chem. Soc., 1940, 62, 441.
↑ H. Rzepa, Pericyclic Reactions' http://www.ch.ic.ac.uk/local/organic/pericyclic/
↑ H. Rzepa, Conformational Analysishttp://www.ch.ic.ac.uk/local/organic/conf/
↑ M.J. Goldstein, M. S. Benzon, J. Am. Chem. Soc., 1972, 94, 7147
↑ F. H. Allen, O. Kennard, D. G. Watson, L. Brammer, A. G. Orpen and R. Taylor, J. Chem. Soc., Perkin Trans. 2, 1987, S1DOI:10.1039/P298700000S1
↑ I Fleming, Frontier orbitals and organic chemical reactions, John Wiley & Sons, 2006, 106-107

[1] A. C. Cope, E. M. Hardy, J. Am. Chem. Soc., 1940, 62, 441.

[2] H. Rzepa, Pericyclic Reactions' http://www.ch.ic.ac.uk/local/organic/pericyclic/

[3] H. Rzepa, Conformational Analysishttp://www.ch.ic.ac.uk/local/organic/conf/

[4] M.J. Goldstein, M. S. Benzon, J. Am. Chem. Soc., 1972, 94, 7147

[5] F. H. Allen, O. Kennard, D. G. Watson, L. Brammer, A. G. Orpen and R. Taylor, J. Chem. Soc., Perkin Trans. 2, 1987, S1DOI:10.1039/P298700000S1

[6] I Fleming, Frontier orbitals and organic chemical reactions, John Wiley & Sons, 2006, 106-107

[1]

[2]

[3]

[4]

[5]

[6]