Rep:Mod:stm

This computational experiment focused on characterising transition structures, reaction paths and activation barrier heights for the Cope rearrangement as well the Diels Alder Cycloaddition reaction. This is achieved using the Gaussian program which utilises MO based methods to numerically solve the Schrodinger equation.

Cope Rearrangement Tutorial

The Cope Rearrangement

The tutorial material centered around the Cope Rearrangement which is a pericyclic [3,3]-sigmatropic rearrangement of 1-5 Hexadiene. The mechanism by which the reaction proceeds has generated some controversy in the past, however it is now widely believed to proceed via a concerted mechanism with a boat/chair transition state. [1] Calculations will be carried out to determine the energy of these transition states from which we can infer which TS is more likely to exist in reality. The results from the computational experiment should also correspond to a concerted mechanism.

The free rotation about the sp3 hybridised C-C single bonds gives rise to a large array of conformations that 1-5 Hexadiene can adopt. [2] One of the anti, as well as one of the gauche conformers were drawn on Gaussview and optimised using the Hartree Fock method (321G) as well as using Density Functional Theory (631G*). The final energies of the structures were compared to the energies provided in Appendix 1 [1] to ensure we had acquired the lowest energy gauche conformation.

1,5 Hexadiene (Anti1 Conformation)

Log file link

A molecule of 1,5 Hexadiene was drawn on GaussView in an antiperiplanar conformation (180° dihedral angle). The structure was first 'cleaned' using the Clean function which modifies the geometry of the molecule in question based on a set of rules in order to present a structure that more closely represents what you would expect from chemical intuition. The final structure given using the clean function is only an approximation and the results would not be accurate enough to use in detailed calculations.

The structure was then optimised using the Hartree Fock/3-21G pople basis set in order to obtain the energy of the molecule. It was ensured that all forces and displacements had converged in the log file of the optimisation. The energy was found to be -231.69260235 a.u. The 'symmetrise' function was then used to ascertain the point group, which turned out to be C2.

Summary Data	GaussView Structure	Point Group
		C2

1,5 Hexadiene (Gauche1 Conformation)

Log file link

The gauche conformer was then drawn with a dihedral angle of 60° and optimised using the same level of theory as detailed above (HF/321G). The energy calculated was -231.68771610 a.u and the point group remained as C2. The energy of this Gauche conformer was found to be higher than that of the anti1 conformer as there is a steric clash between the terminal unsaturated bonds.

Summary Data	GaussView Structure	Point Group
		C2

1,5 Hexadiene (Gauche3 Conformation)

Log file link

The same calculation as outlined above (HF/3-21G) was carried out for the Gauche conformation (62.75° dihedral angle) of 1,5 Hexadiene and returned an energy of -231.68772 Hartree units. The point group transpired to be C1. The results that were acquired were quite curious as they suggest the Gauche conformation lies lower in energy than the previously calculated antiperiplanar conformation despite the gauche conformation having more steric strain. Rationale for this observation can be found by computing the MO's for the Gauche conformation which has been done below, and it can clearly be seen that there is an extra favorable electronic bonding stabilisation interaction in the gauche conformation between the terminal π orbitals of the molecule.

Summary Data	GaussView Structure	Point Group
		C1

Nf710 (talk) 18:45, 4 November 2015 (UTC) This is an excellent example of how we use guassian/gview to solve these problems. You have clearly shown graphically why we get the gauche 3 conf at a lower energy. well done as you have clearly gone beyond the script and independently thought how to visualise this, Clearly the MOs here show second order interactions which lead to a lower energy. your calculation of energy and point group are also correct.

1,5 Hexadiene (Anti 2 Conformation)

Log file link

HF/3-21G energy: -231.6925 Hartree units. Point Group Ci. In order to more easily find the correctly optimised conformer, the symmetrise function was used with relaxed tightness and the molecule was allowed to adopt the Ci point group before the optimisation was run.

Summary Data	GaussView Structure	Point Group
		Ci

1,5 Hexadiene (Anti 2 Conformation Optimised using DFT)

Log file link

The structure above was reoptimised using a higher level of theory, namely DFT/B3LYP/6-31G* (Density Functional Theory). In addition, a frequency calculation was also carried out in order to confirm we have located an energy minimum by ensuring all vibrational frequencies in the molecule are positive and real numbers. This basis set is more precise as it employs a function of another function, namely spatially dependent electron density and electron correlation effects. [3] The energy was found to be -234.61171166 a.u. This value cannot be directly compared to the energy computed using the HF 321G basis set as it is meaningless to compare energies from different basis sets.

Nf710 (talk) 18:52, 4 November 2015 (UTC)DFT is generally more precise and cheaper. here however they have used a more expansive basis set of 6 orbitals which can better 'mould' the electron around the molecule to its true energy. DFT can be better than HF because it takes into account spin and pairing energy (correlation effects) and it doesn't try and solve the whole many electron shrodinger equation with a single slater determinant. This can become very expensive with larger basis sets. further more HF treats the electronic repulsion as a function of a mean field which typically over estimates this term because its a function of all the electrons when it should be all of the electrons minus one because it is the repulsion on each electron. DFT uses functional of the electron density which get around this problem.

Summary Data	GaussView Structure	Point Group
		Ci

A comparison between the final geometries using the two different basis sets is given below.

	Bond Length Å			Dihedral Angle °	Point Group
	Terminal C1-C2	C2-C3	Central C3-C4	C1-C2-C3-C4
HF, 321G	1.316	1.509	1.553	-114.67	Ci
DFT, B3LYP, 631Gd	1.334	1.504	1.548	-118.59	Ci

The table above shows that there is only a very slight discrepancy between the geometries of the molecule optimised with different basis sets. The point groups are also identical. This exercise shows that more precise basis sets have a greater computational cost, and that less precise basis sets will often give similar results.

Nf710 (talk) 18:58, 4 November 2015 (UTC) Good comparison of geometries

Frequency Calculations

A frequency calculation was carried out and enabled us to confirm that we have characterized the critical point by ensuring no imaginary frequencies exist and all frequencies are real, positive numbers. The IR spectra in Figure Y was acquired. No negative 'imaginary' frequencies on the IR spectra indicates that we have not found a transition state. The IR peaks are classified in the table below.

Bond Type	Frequency (cm-1)
CH2 Wag	900
sp2/sp3 C-C stretches	3000-3200

The Thermochemical data in Figure X was also obtained from the frequency calculation. The calculation for the first row (Sum of electronic and zero point energies) has been calculated at 0K, whilst the other calculations have been performed at 298.15K and 1atm. The zero point energy is the lowest possible energy a quantum mechanical system may have. As the bonds in hexadiene are modeled by the quantum harmonic oscillator, the zero point energy accounts for the residual vibrational energy. In contrast, the calculations performed at 298.15K will possess elements of translational, vibrational and rotational energy. [4]

The equation to obtain the thermal enthalpy at constant pressure is given by H=E+RT (H=enthalpy, E=energy, R=gas constant, T=temperature). Note that at 0K RT=0. therefore H=E. If T≠0K then H≠E. This relationship is reflected in the calculations.

Entropic contributions to the energy are taken into account in the sum of electronic and thermal free energies (H=G+TS) calculation. Note that this calculation is performed at constant pressure. As the temperature increases, the value of H will increase accordingly. Gaussian uses the following partition function to provide a value for the entropy.

Nf710 (talk) 19:04, 4 November 2015 (UTC) You have really well explained the theory behind the energies with elements of statistical mechanics and quantum mechanics. Also your computed frequencies and energies are correct.

Chair/Boat TS Optimisation

In this section we will optimise transition structures using 3 different methods, as well as running the Intrinsic Reaction Coordinate and calculating activation energies for the Cope rearrangement. Transition state structures can be found by searching the potential energy surface (PES) for saddle points.

(i) Computing Force Constants

Log file link

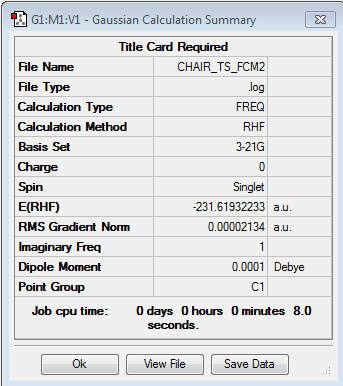
We set out to optimise the chair transition state using this 'local search' method which involves making an initial guess of the TS which must possess a corresponding Hessian matrix with one negative eigenvalue. We started by drawing and optimising an allyl fragment using the HF/321G basis set. This allyl fragment was then copied and pasted, and the resulting species was reoriented so the terminal carbons were 2.2Å apart and the final structure resembled a chair TS. It is imperative that the structure drawn on GaussView resembles the TS as closely as possible as if it does not, it is likely that the curvature of the potential surface will be significantly different at points that are far away from the TS.

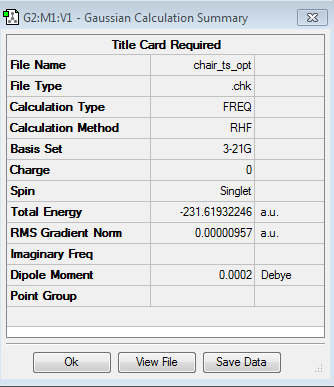
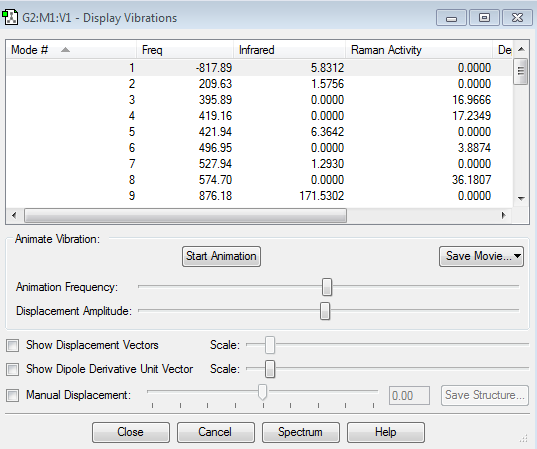
We then proceeded to set up a Gaussian optimisation for a TS using the TS(Berny) method with the force constants being chosen to be calculated once. Note that Opt=NoEigen was added in the keyword section in order to prevent the program from crashing in the event that more than one imaginary frequency is located. As the table below shows under the calculated frequencies column, we succeeded in locating only one imaginary frequency at -818.05 cm^-1 thus confirming we have found a TS.

The reason we call the TS negative frequency an imaginary frequency may be because when the force constant, k, gets calculated for a TS it turns out to be negative. At a transition state, the force constant will be negative as the force will be in the opposite direction to the displacement. The equation for finding the frequency as a function of the force constant involves square routing the force constant k. Square routing a negative number will give you an imaginary number, hence the term imaginary frequency.

Nf710 (talk) 19:08, 4 November 2015 (UTC) You have understood the theory here however you could have possible made the explaination better by saying the second differential of the gradient = the curevature of the PES at that point and possible the equations for how the energy levels are derived.

Summary Data	GaussView Structure	Calculated Frequencies	Transition State

(ii) Frozen Coordinate Method

Log file link

One more the aim was to optimise the chair transition state. There are 3N-6 degrees of freedom on a PES. [5] Some of these degrees of freedom can be eliminated from a TS Optimisation by 'freezing' the positions of certain aspects of the geometry such as bond angles and bond lengths. This is done using the Redundant Coordinate Editor on GaussView. The other atoms and geometries that have not been frozen will continue to be optimised as normal. The keyword Opt=ModRedundant is utilised in this calculation in order to ignore any redundant internal coordinates before the calculation is performed.

The distance between the carbon atoms in terminal positions were set at 2.1Å before running the HF/TS(Berny) calculation at the 321G basis set. Once again, we acquired only one imaginary frequency at -817.89cm^-1 thus confirming we have found a TS which corresponds to the TS found by computing force constants.

Summary Data	GaussView Structure	Calculated Frequencies	Transition State

COMPARISON OF TS METHOD 1 TO METHOD 2

(iii) QST2 Method

Log file link

The boat transition state is another feasible alternative to the chair transition state and we attempted to optimise the boat TS using the QST2 method. The Synchronous Transit-guided Quasi-Newton method (QST2) method is a chain of state method that located a TS based on the geometry of the starting reactant and the final product.

Before running the QST2 calculation, we had to ensure that both the reactant and the product had been labelled consistently to avoid any errors. The first time we ran the calculation using the linear molecules, the optimisation failed. So we edited the bond angles such that the structure represented the TS more closely before trying the optimisation again.

Labelled Optimised Boat Molecules	TS Vibration

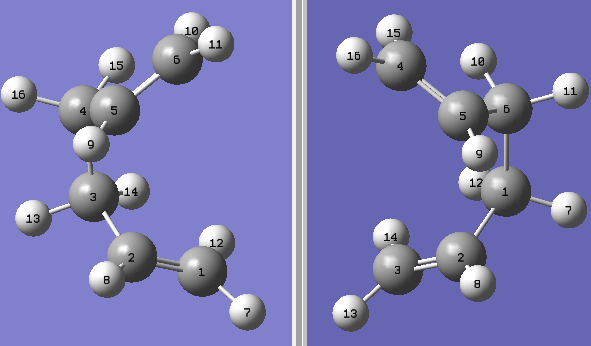
It is not possible to tell which of the many 1,5 Hexadiene conformers the TS we have located will lead to. The IRC method discussed in the next section helps answer this question.

(iv) Intrinsic Reaction Coordinate (IRC)

Log file link

IRC calculations start at the transition state and follow the line at which there is the steepest gradient on the PES in order to locate the adjacent local minimum. You can set the calculation to do this in either one direction or in both directions. This is useful as you will be able to determine whether the transition state that has been found successfully connects the reactant and the product as well as being able to locate any reaction intermediates. It should be noted that the number of steps in an IRC can be set manually, and if the number is not set high enough the minimum geometry will not be located. Conversely, if the number of steps is set too high it is possible for IRC to follow an alternative low energy path after a while. Another potential issue that must be considered is to be careful you do not confuse an intermediate with a product as both chemical species will have a gradient of zero on the IRC graph.

We first performed the IRC on the chair transition state conformation that we obtained using the Frozen Coordinate Method earlier on. The IRC was at first attempted with 50 steps and the results are shown below. Note that the IRC stopped after 44 steps and seemed to plateau out in energy. Another IRC with 70 steps was run in order to confirm that the IRC had indeed arrived at the correct structure. The energy of the structure obtained at the 44th point of the IRC is -231.692 a.u.. An optimisation ran at the HF/321G level on the 44th point of the IRC confirmed that the energy was -231.69166702 a.u. and the point group of C2 which corresponds to the Gauche2 conformer of Appendix 1. Within rounding errors, these energy values are identical to one another and confirm that the correct gauche2 conformer has been located.

Nf710 (talk) 19:12, 4 November 2015 (UTC) It is not necarcerry to do 70 steps if you look int he .log file you should see that the energy has converged. As the gradient will be zero.

IRC	Reaction Path

(iv) Activation Energies

The final task of the cope rearrangement tutorial involved calculating the activation energy for the Cope Rearrangement via both the chair and boat transition structures. Both of the TS were reoptimised and frequency calculations carried out using the DFT/B3LYP/6-31G* level of theory. The optimised transition structures using the HF/321G level of theory were used as input files in order to reduce the computational cost of the calculation. Upon initial inspection of the images for the transition structures, there seems to be little difference between the lower accuracy 321G HF method and the B3LYP 631G* method. The higher level of DFT theory has been compared to the lower level of HF theory below quantitatively in terms of energy and geometry. The separation between the allyl fragments have been tabulated for the different basis sets used above and it can be seen that the higher level of theory returns values very similar to the lower level of theory (2.50% and 3.03% percentage differences respectively). In contrast, a comparison of the energies acquired at both 0K and 298.15K shows that there are marked differences of approximately 3 a.u. in the values computed for the different basis sets. (N.B To obtain the electronic energy of the chemical species the zero point correction energy has been subtracted from the sum of electronic and zero point energies)

Method	Chair TS Seperation (Å)	Boat TS Seperation (Å)
HF/321G	2.020	2.140
DFT/B3LYP/631G*	1.970	2.207

	Electronic Energy (HF/321G)	Electronic + Zero Point Energy (0K) (HF/321G)	Electronic + Thermal Energy (298.15K) (HF/321G)	Electronic Energy (B3LYP/631G*)	Electronic + Zero Point Energy (0K) (B3LYP/631G*)	Electronic + Thermal Energy (298.15K) (B3LYP/631G*)
Chair TS	-231.619304	-231.466697	-231.461338	-234.556934	-234.414886	-234.408956
Boat TS	-231.602165	-231.450929	-231.445300	-234.543093	-234.402342	-234.396007
Anti2 Conformer	-231.692535	-231.539539	-231.532566	-234.611712	-234.469215	-234.461867

	HF/321G Activation Energy at 0K (kcal/mol)	HF/321G Activation Energy at 298.15K (kcal/mol)	B3LYP/631G* Activation Energy at 0K (kcal/mol)	B3LYP/631G* Activation Energy at 298.15K (kcal/mol)
Chair TS	45.709	44.696	34.092	33.202
Boat TS	55.604	54.760	41.963	41.328

The energies obtained were compared to literature values in order to see which of the basis sets aligns more closely with experimental data. In order to be able to do this the values provided in Gaussian in atomic units must be converted to kcal/mol using the conversion factor 1 a.u=627.51 kcal/mol. The experimental values for this reaction taken from the lab script at 0 K are 33.5 ± 0.5 kcal/mol for the Chair TS and 44.7 ± 2.0 kcal/mol for the Boat TS. The activation energy itself is defined as the minimum quantity of energy that the reacting species must possess in order to undergo a specified reaction. We can calculate the activation energy by taking the difference between the energy of the lower energy chair TS and the reactant at a particular temperature.

It can be concluded that the higher basis set makes a more discernible difference to the computed energies of the molecule rather than the computed geometries, thus it would suffice to use the HF/321G basis set if you are only interested in attaining an accurate geometry for a molecule and you are not interested in its energy as its computational cost it less. The higher basis set also agrees more closely with the provided experimental data. The differences between the experimental data and the computed data could be attributed to the many approximations gaussian makes in its calculations, as well as the fact that you are performing calculations on a single molecule when in reality intermolecular forces will come into play.

Nf710 (talk) 19:26, 4 November 2015 (UTC) In all this is a good piece of work. you have gone into a lot of detail with the work and written lots. perhaps at times you could have been more consise. and perhaps tabulated more of your data. your electronic energies seem to be slightly out but everything else seems ok. You have also compared the geometries and energies of the basis concluding that if you care about geometry a lower basiss can be fine, however energies need larger ones.

The Diels-Alder Cycloaddition

Diels Alder Cycloaddition

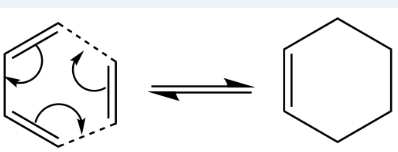
In this section of the computational exercise, the Diels Alder (DA) cycloaddition is investigated by characterisation of transition structures as well as analysis of molecular orbitals. The DA [4+2] cycloaddition falls under the category of pericyclic reactions and proceeds by a diene and a dienophile reacting with the formation of 2 sigma bonds and breaking of 2 pi bonds in a concerted manner via a cyclic TS. The formation of the sigma bonds is thermodynamically favorable and helps drive the reaction forward. The reaction is either described as normal electron demand or inverse electron demand. The difference lies in the relative energies of the HOMO and LUMO of the reactants. In the normal electron demand reaction, the diene contains EDG increasing the energy of the HOMO whlist the dienophile containing EWG lowering the energy of its LUMO. Reducing the difference in energy between the HOMO and LUMO facilitates the reaction. In an inverse electron demand reaction, the EDG and EWG are placed on the other reactant with the same end result of reducing the HOMO LUMO energy gap. If the HOMO and LUMO have the same orbital symmetries as well as having a non zero overlap integral then the reaction is said to be allowed. [6] Forbidden DA reactions do not fulfill either of these conditions. The Woodward Hoffman rules can also be used to determine whether the reaction is thermally allowed or forbidden.

Secondary orbital effects play an important role in these reactions. If the dienophile is subtituted with appropriate groups, extra orbital interactions occur that can stabilise the product and lead to regiochemistry. A mixture of products named the exo and endo products is formed due to this effect.

Throughout this exercise, the AM1 semi-empirical method has been employed as the basis set. This method has a smaller computational cost than other methods due to the two electron integral part of the Hamiltonian not being included.

Cis-butadiene + Ethene Reaction

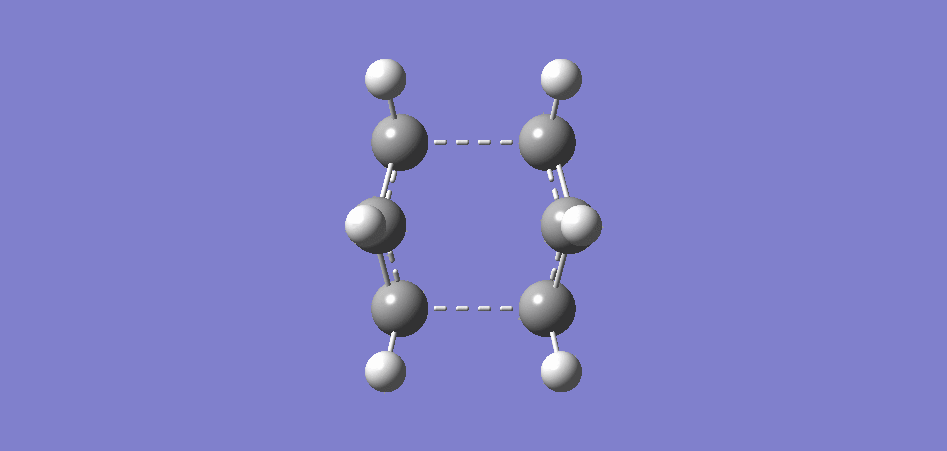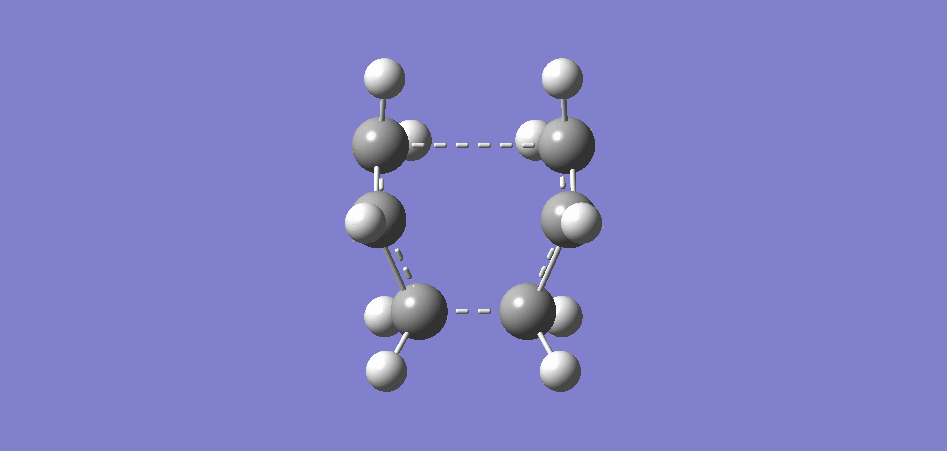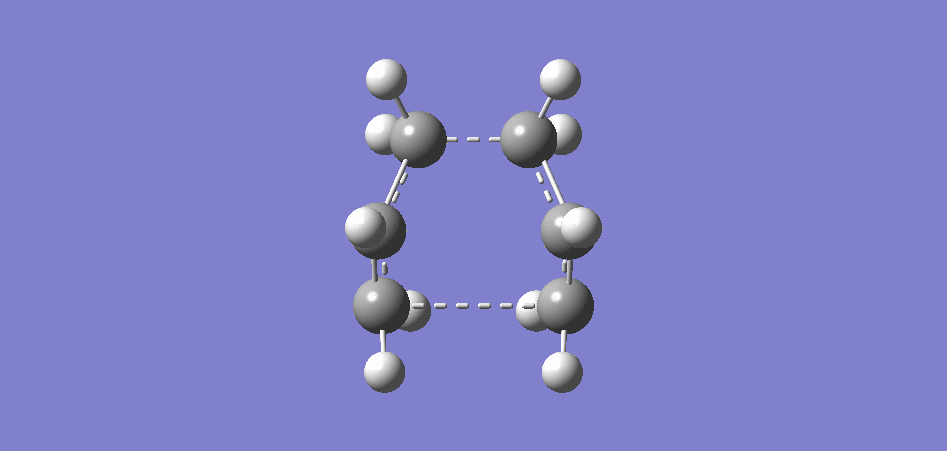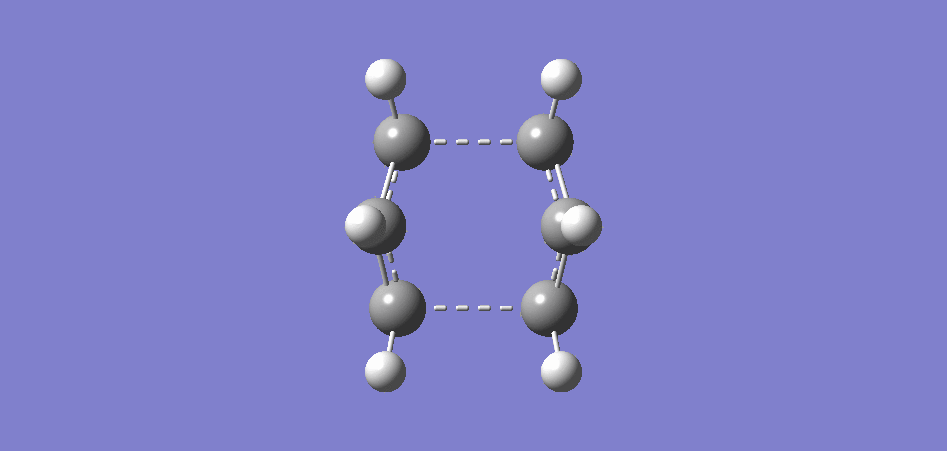
GaussView was used to draw a molecule of cis-butadiene with a dihedral angle of 0° and the point group was symmetrised to C2V. A picture of the symmetric LUMO as well as the antisymmetric HOMO is given below. The HOMO is antisymmetric with respect to a plane across the centre of the molecule that doesn't touch any orbitals.

Cisbutadiene LUMO	Cisbutadiene HOMO

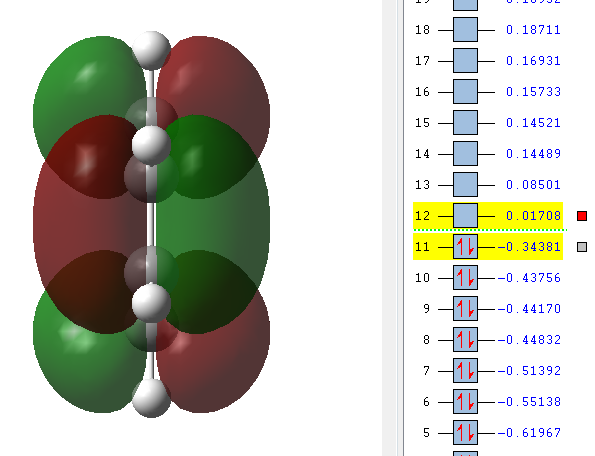
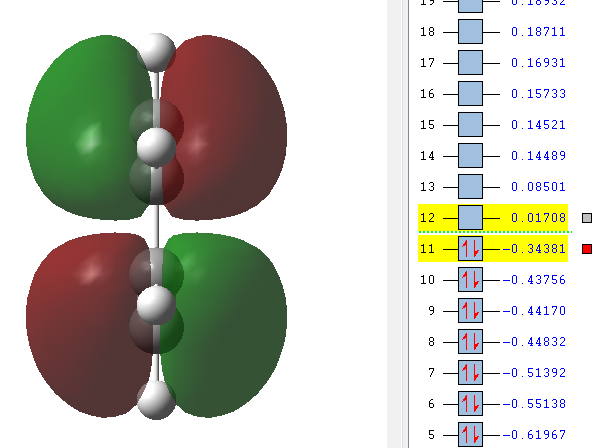
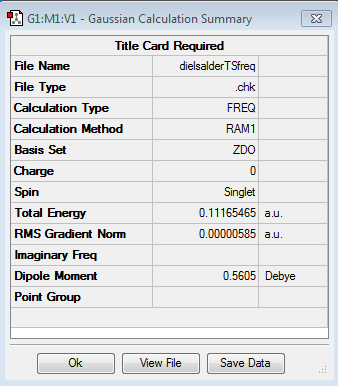
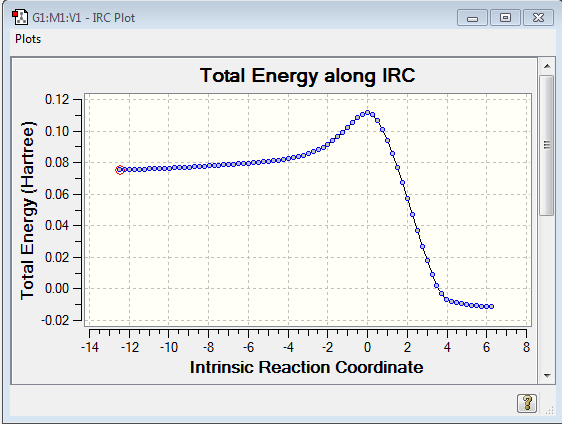
We then set about locating the transition structure for the reaction. The reactants were both optimised and were orientated in an envelope structure in order to maximise the overlap integral between the relevant orbitals. The point group was set as C_s , and an optimisation to TS State (Berny) was run. (Log file link). The calculation was successful as evidenced by the presence of only one imaginary frequency. (-956.09cm^-1) Energy: 0.11165465 a.u. An IRC was also run in both directions from the TS to determine that there is only one TS. If there is more than one peak on the IRC, that would indicate that there is an alternative TS or intermediate in the reaction pathway. From the animation showing the vibration of the TS it can also be seen that the reaction is concerted as the bonds appear to be being made/broken at the same time.

Summary Data	DA Transition Structure	TS Animation	Lowest Real Frequency

IRC	IRC Animation

The IRC shows that the energy of the TS is closer to the reactant than the product, thus defining the TS as an early TS. Hammond's Postulate tells us that this means the TS resembles the reactant more closely, which can also be seen in the TS animation.

We next attempted to identify the HOMO and LUMO's of the TS by visualising the MO's in order to distinguish whether this reaction in particular is normal electron demand or reverse electron demand. As the HOMO of butadiene is higher in energy than the HOMO of ethene we can classify this particular reaction as normal electron demand. Upon further inspection we can see that the HOMO and LUMO of the diene and dienophile respectively come together to give rise to the TS symmetric LUMO. The converse also holds true, with the LUMO of the diene and the HOMO of the dienophile coming together to form the TS antisymmetric HOMO.

LUMO of TS - symmetric

HOMO of TS - antisymmetric

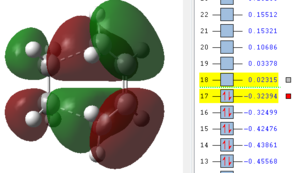
(A comparison of bond lengths to literature were asked for here, as well as commenting on whether the reaction proceeded synchronously or not. I can see you've put that in the next section Tam10 (talk) 10:23, 28 October 2015 (UTC))

Cyclohexa-1,3-diene + Maleic Anhydride Reaction

The next DA reaction that we analyse is the normal electron demand reaction between Cyclohexa-1,3-diene and Maleic Anhydride. The maleic anhydride is electron poor as a result of the carbonyl group substituents it possesses whilst the diene is electron rich as a result of the positive inductive effect of the R groups donating electron density in towards the pi bond. Secondary orbital effects play a significant role in this particular reaction and we will analyse both the endo and exo products that come about.

(i) Exo TS

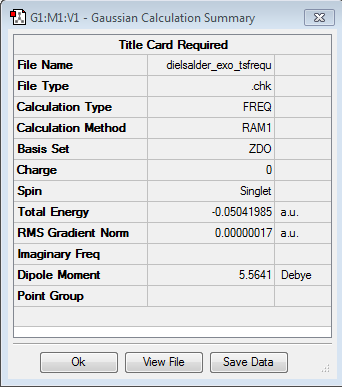
Once again, a TS estimate was drawn by drawing the two reactants, optimising them and orientating them into the guess positions before running a TS (Berny) optimisation using the same AM1 semi empirical method as before. (log file link). The guess position involved the fragments being placed 2Å apart. Point Group: C_s. The final energy of the TS transpired to be -0.05041985 a.u with the singular imaginary frequency coming in at -812.19 cm^-1

TS Data Summary	DA Exo TS	TS Animation

C1-C4 (Å)	C2-C3 (Å)	C3-C4 (Å)	C2-C21 (Å)	C18-C21 (Å)	C9-C11 (Å)	C2-C9 (Å)	Labelled Exo TS
1.39438	1.39438	1.39676	1.48976	1.52208	1.41011	2.17040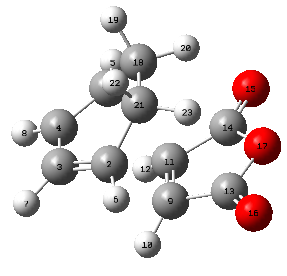

C1-C4, C2-C3, C3-C4 and C9-C11 all have bond lengths that are in between that of a sp3 (1.54Å) and sp2 (1.33Å) hybridised carbon. These are the bonds that are either breaking/forming a new bond in a synchronous manner. It should also be noted that C1-C11 and C9-C2 have separations smaller than the overall sum of two VDW radii indicating that there is some form of electronic interaction.

LUMO +2	LUMO +1	LUMO	HOMO	HOMO -1

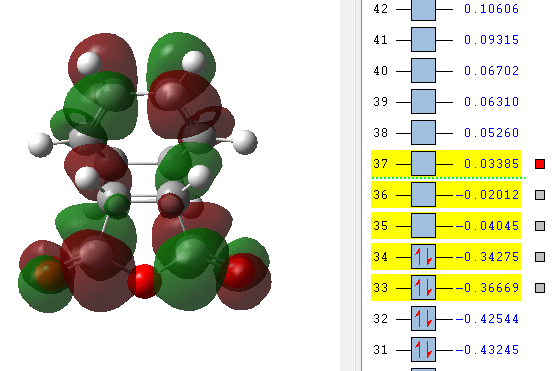
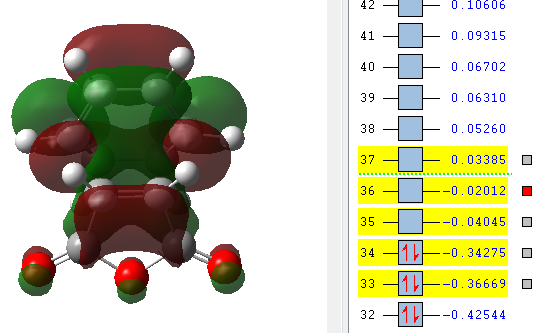
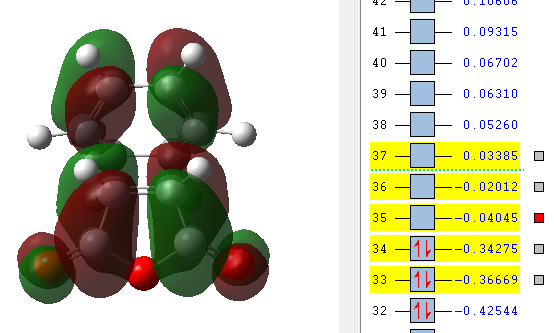
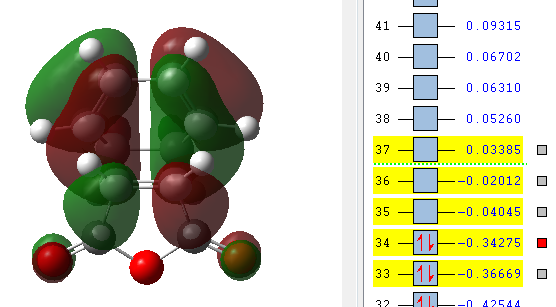
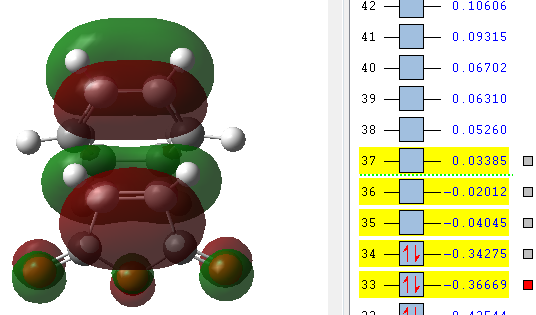
The orbitals that have been computed are shown above. The most important observation that can be made is the fact that ONLY primary and no secondary orbital interactions are occurring. This is simply due to the proximity of the C=O π^* and C=C π antisymmetric orbitals being too far apart to interact to any degree. The absence of secondary orbital interactions explains why the exo TS lies higher in energy than the endo TS. For the exo diastereomer, both the HOMO and LUMO are antisymmetric. Note that the more nodal planes there are between the atoms of the molecule, the higher the energy is raised.

An IRC was then run which provided an animation showing the concerted reaction involving syn addition.

IRC Animation

(ii) Endo TS

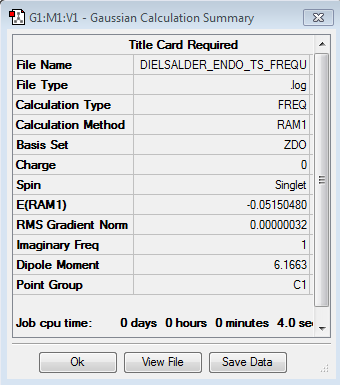
The same process as was used in locating the Exo TS was used once more. The optimised reactant fragments were orientated such that the C=C bonds in hexadiene were directly on top of the C=O bonds in Maleic anhydride.

Computed TS energy using AM1 Semi Empirical method (log file link): -0.05150480 a.u.

Imaginary Frequency: -806.39 cm^-1. Point Group: C_s

TS Data Summary	DA Endo TS	TS Animation

C1-C4 (Å)	C2-C3 (Å)	C3-C4 (Å)	C2-C21 (Å)	C18-C21 (Å)	C9-C11 (Å)	C2-C11 (Å)	Labelled Endo TS
1.39305	1.39724	1.39305	1.49053	1.52297	1.40849	2.16239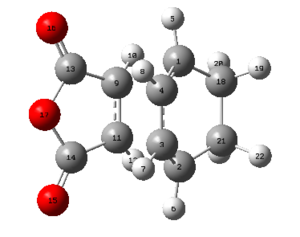

The bond lengths tabulated above once more show that delocalised bonds with bond lengths intermediate to that of a single C-C and a double C=C bond are present, as in the exo TS. The distance between C2 and C11 turns out to be less than the overall sum of the VDW radii of two carbon atoms, once more suggesting that there is some form of bonding interaction occurring.

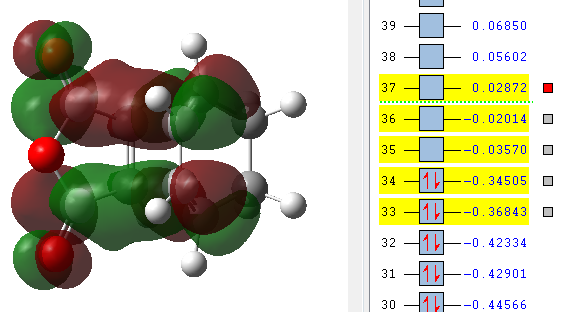
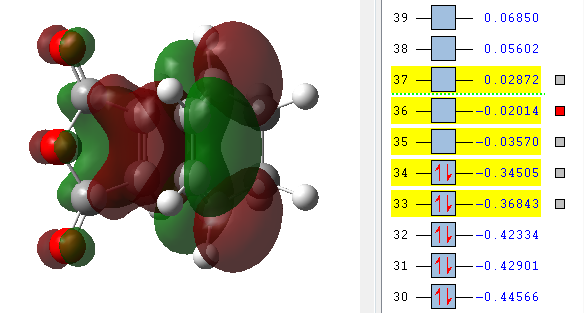
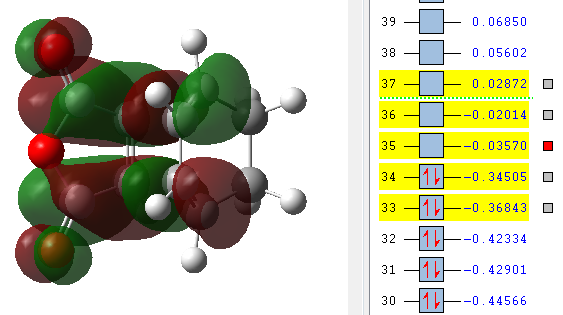
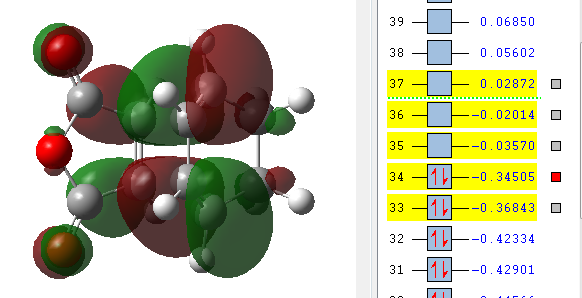
LUMO +2	LUMO +1	LUMO	HOMO	HOMO -1

The MO's above were computed and it can be seen that there is considerable levels of orbital overlap between the π* orbital of the C=O bond in the dienophile and the π orbitals in the C=C of the diene. This is a good illustration of the effect that was alluded to earlier, the secondary orbital overlap, which provides a stabilising effect so great that it kinetically overcomes the increased levels of steric repulsion that is felt due to the carbon backbone of the product being more compressed. Something else that can be seen in the MO visualisations is the differing bonding coefficients that come about due to the difference in electronegativity between Oxygen and Carbon atoms. For the endo diastereomer, both the HOMO and LUMO are antisymmetric.

An IRC was also run on the Endo DA TS to be able to visualise the concerted process taking place, implying the two new C-C sigma bonds formed synchronously.

IRC Animation	IRC

(iii) Activation Energies

The activation energies were calculated in the same manner they were calculated earlier on in the experiment. After optimising the reactants the activation energies are as given below...

	Maleic Anhydride	1,3 Cyclohexadiene	Exo TS	Endo TS	ΔE Exo	ΔE Endo
Energy a.u.	-0.121823	0.027711	-0.050420	-0.051505	0.043692	0.042610

(You should convert your units into something more relatable, like KJ/mol or Kcal/mol. Of course, this would only make sense for activation energies and reaction enthalpies Tam10 (talk) 10:23, 28 October 2015 (UTC))

Conclusion

It was found in the first section of this computational experiment that the chair TS in the Cope rearrangement is lower in energy than the boat TS, thus meaning that the activation energy for the reaction via a chair TS is lower meaning that this reaction pathway is kinetically favourable. In the latter portion of the experiment, the DA reaction was investigated and it was found that endo selectivity is favored, despite the exo product being more thermodynamically favorable. This comes about due to secondary orbital effects making the endo diastereomer kinetically favorable.

It should not be forgotten that computational calculations make a series of assumptions when coming to their final answers. One example of an effect that is neglected in these calculations is the Frontier Orbital approximation. [7] Reactive DA reactions like the ones we are studying are said to have early 'loose' transition states. Increases in reactivity correspond to smaller HOMO LUMO energy gaps, meaning that the reactants do not need to be as close to one another in order to successfully react. Consequently, the frontier overlap is small and can be neglected.

It would be interesting to study further Diels Alder reactions that use 4-Chloro-2(H)-pyran-2-one [8] as a reactant. The dienophile in this example is monosubstituted, is electron deficient and leads to a mixture of 4 products (2 endo, 2 exo) that are substituted bicyclic lactone cycloadducts. A future computational study could involve using DFT calculations to make sense of the selectivity in the reaction.

References

[1] Imperial College London, Computational Chemistry Wiki https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3#Appendix_1

[2] Wiest, Olaf, Kersey A. Black, and K. N. Houk. 'Density Functional Theory Isotope Effects And Activation Energies For The Cope And Claisen Rearrangements'. J. Am. Chem. Soc. 116.22 (1994): 10336-10337. Web. 23 Oct. 2015.

[3] Van Mourik, Tanja; Gdanitz, Robert J. (2002). "A critical note on density functional theory studies on rare-gas dimers".Journal of Chemical Physics 116 (22): 9620–9623. Bibcode:2002JChPh.116.9620V. doi:10.1063/1.1476010

[4] What is the 'zero-point energy' (or 'vacuum energy') in quantum physics? Is it really possible that we could harness this energy?". Scientific American. 18 August 1997.

[5] Reif, F. (2009). Fundamentals of Statistical and Thermal Physics. Long Grove, IL: Waveland Press, Inc. p. 51. ISBN 1-57766-612-7.

[6] Longuet-Higgins, H. C.; Abrahamson, E. W. (1965). Journal of the American Chemical Society 87 (9): 2045

[7] J. Pople and D. Beveridge, " Approximate Molecular Orbital Theory ", McGraw-Hill., 1970

[8] Kamyar Afarinkia ,* Michael J. Bearpark , andAlexis Ndibwami" " Computational and Experimental Investigation of the Diels−Alder Cycloadditions of 4-Chloro-2(H)-pyran-2-one " ", J. Org. Chem., 2003, 68, '19 ', 7158-7166.DOI:10.1021/jo0348827 10.1021/jo0348827