Rep:Mod:stl14

Introduction

By employing different basis set, a molecular geometry can be optimised to a minimum by solving the Schrodinger equation using Gaussian. A potential energy surface(PES) can be plotted from the energy gained from quantum chemistry as a function of the position of nuclei provided Born Oppenheimer approximation is valid. A minimum on the PES corresponds to the physically stable chemical species with a zero gradient and a positive secondary derivatives. On the other hand, a maximum on the PES, which is also called the saddle point is the transition state with a zero gradient and a negative secondary derivatives. A transition state has the highest energy on the reaction coordinate which connects a reactant to a product. The reactant must have sufficient energy to overcome the energy barrier for a reaction to occur. By running a frequency calculation, the minimum on the PES can also be determined. The vibrational modes of a global minimum will have all positive frequencies whereas transition state will have one imaginary frequency due to its negative secondary derivatives (maximum on PES).

In the exercises below, the methods employed to optimised the molecules are the semi-empirical (PM6) and DFT (B3LYP/6-31G(d) level). DFT produces more accurate results than semi-empirical method on Gaussian as it uses higher level basis set. However, PM6 takes shorter time to complete the calculation as it requires less computational effort. Hence, all the molecular geometries were optimised first with PM6 followed by B3LYP to obtain more reliable results.

Nf710 (talk) 20:57, 7 February 2017 (UTC) A TS only has 1 negative frequency and therefor only has 1 reaction co ordinated which is a maximum. it is not a global maximum on the PES like you have written.

Exercise 1: Reaction of Butadiene with Ethylene

Reaction Scheme

Figure 1. The Diel-Alders reaction of butadiene and ethene.

MO diagram for the formation of butadiene/ethene TS

Figure 2. The MO diagram for the formation of butadiene/ethene TS.

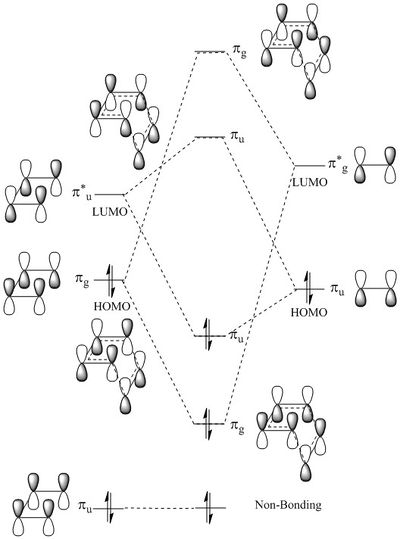
Nf710 (talk) 20:59, 7 February 2017 (UTC) This is a very nice MO diagram. But you have used u and g which suggests a center of inversion which is not true.

Molecular Orbitals

Name of compound	Orbital	Symmetry	Image of MOs (JSmol)
Butadiene	HOMO	g
Butadiene	LUMO	u
Ethene	HOMO	u
Ethene	LUMO	g
TS	HOMO	symmetric
TS	HOMO	unsymmetric
TS	LUMO	unsymmetric
TS	LUMO	symmetric

Figure 3. The MOs of reactants and TS.

The all-bonding orbitals (u) of butadiene remain non-bonding in the MO diagram as it lies too low in energy to react. The HOMO of the butadiene (g) reacts with the LUMO (g) of the ethene to form the secondary HOMO and LUMO of TS. On the other hand, the HOMO (u) of ethene reacts with the LUMO (u) of butadiene to form the primary HOMO and LUMO of TS. The MOs drawn in the MO diagram are in good agreement to the MOs generated by Gaussview. In order for a reaction to occur, the symmetry of the reactants must be the same. For example, gerade-gerade or ungerade-ungerade interaction is allowed whereas gerade-ungerade interaction is forbidden. Hence, the orbital overlap integral is non-zero for symmetric-symmetric and asymmetric-asymmetric interaction but zero for symmetric-asymmetric interaction.

Bond length measurement

Compound	Images	Bond Length (Å)
Butadiene		C1C2=C3C4= 1.335 C2C3= 1.468
Ethene		C1C2= 1.327
TS		C1C2=C3C4= 1.380 C2C3= 1.411
TS		C1C2= 2.116, C3C4= 2.113 C2C4= 1.382
Product		C1C2= C3C4= 1.500 C2C3= 1.338
Product		C1C2= 1.539, C3C4= 1.540 C1C3= 1.541

Figure 4. The measurement of different C-C bond lengths.

The bond distance between the terminal carbons of butadiene and carbons of ethene decreases as they approach each other to form single bonds. As a result of Diels-Alder reaction, the double bonds elongate to form single bonds whereas the single bond is shorten to form double bond. The typical sp³ and sp² C-C bond lengths are 1.544 Å and 1.337 Å respectively. The single (1.500-1.541 Å) and double (1.338 Å) C-C bonds formed in the product are comparable to the typical sp³ and sp² C-C bond lengths. The Van der Waals radius of the C atom is 1.700 Å . The bond length between the carbons of butadiene and ethene is shorter than the expected value (3.4 Å) in the TS due to the bond forming interaction.

Vibration

Figure 5. Illustration of the TS vibration.

The vibration of the TS at -949 cm^-1 is shown above. This is the imaginary frequency at which the butadiene and ethene approach each other to form single bonds. The formation of the two single bonds are synchronous as illustrated in figure 5. The stretching of the C=C double bonds and the compression of the single bonds compliment the trend of the bond distances as discussed above. On the other hand, the lowest positive frequency at 145 cm^-1 shows that this vibration mode does not bring the two reactants together in the TS and hence not contributing to the formation of product.

Good first section. The only thing that that was wrong was the symtry of the product orbitals in the MOs diagram, but it was correct in the table. Also it would have been nice if you could have shown some understanding of the theory behind the methods you are using.

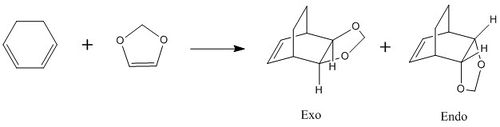
Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole

Reaction Scheme

Figure 6. The Diel-Alders reaction of cyclohexadiene and 1,3-dioxole.

Molecular Orbital

Transition state MOs	MO	Symmetry	Type of product
	HOMO	Symmetric	Exo
	Secondary HOMO	Antisymmetric	Exo
	LUMO	Symmetric	Exo
	Secondary LUMO	Antisymmetric	Exo
	HOMO	Symmetric	Endo
	Secondary HOMO	Antisymmetric	Endo
	LUMO	Symmetric	Endo
	Secondary LUMO	Antisymmetric	Endo

Figure 7. MOs of exo /endo TS (generated at B3LYP/6-31G(d) level)

MO diagram

Figure 8. The Diel-Alders reaction of butadiene and ethene.

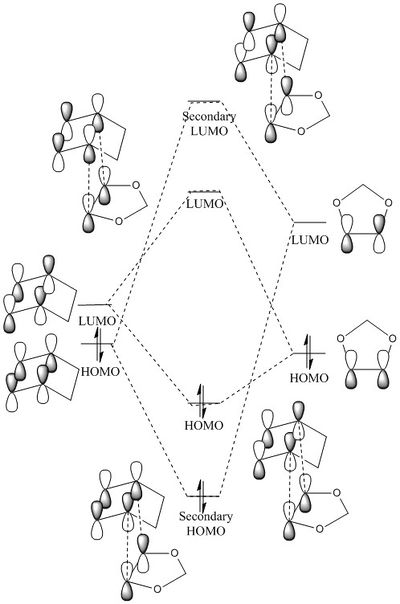
The HOMO and LUMO of the transition state are formed via the interaction between the HOMO of the 1,3-dioxole (dienophile) and the LUMO of the cyclohexadiene (diene) as shown in the MO diagram above. The interaction between the HOMO of diene and LUMO of dienenophile generates the secondary HOMO and LUMO in TS. The HOMOs and LUMOs of the dienophile and diene have the same symmetry to react. The orbitals in 1,3-dioxole dominates over the orbitals from cyclohexadiene in the HOMO of TS as observed in figure 7. The dienophile is electron rich which due to the presence of the electron donating group in 1,3-dioxole which increases its HOMO energy level. The diene LUMO and dieneophile HOMO are closer in energy and interact stronger than the HOMO of the diene and LUMO of the dienophile. Hence, this is an inverse electron demand DA reaction.

Energies

Sum of electronic and thermal free energies (Hartree)						Energy barrier (kJ/mol)	Reaction energies (kJ/mol)
	Cyclohexadiene	1,3-dioxole	Reactants	TS	Product
Exo	-233.321033	-267.068132	-500.389165	-500.329168	-500.417321	157.52	73.92
Endo	-233.321033	-267.068132	-500.389165	-500.332149	-500.418691	149.70	77.52
Table 1: Values of the sum of electronic and thermal Free Energies (calculation ran at B3LYP/6-31G(d) level)

The endo product has a lower energy compares to exo product and thus it is thermodynamically more stable. The energy barrier from the reactant to the endo product is lower than that of exo which causes it to be kinetically favourable. Therefore, endo product is both kinetically and thermodynamically favourable.

From figure 7, the HOMO of the endo TS shows secondary orbital interaction between the p-orbitals from the oxygen atoms on 1,3-dioxole and p-orbitals from diene. This will lowers the energy barrier which is kinetically favourable. The HOMO of the exo TS does not show any secondary orbital interaction. Besides that, there is no steric effect in the HOMO of endo TS as the sp³ carbon centres of both the diene and dienophile are pointing in opposite direction. On the other hand, steric effect is observed in exo TS as the sp³ carbon centres of both the diene and dienophile are pointing in the same direction which causes it to be kinetically and thermodynamically unfavourable.

Nf710 (talk) 21:10, 7 February 2017 (UTC) Excellent second section. very consise, your energies are pretty much correct and you have got the correct conclusion for the thermo and kenetic products. very nice used of jmols also. well done.

Exercise 3: Diels-Alder vs Cheletropic

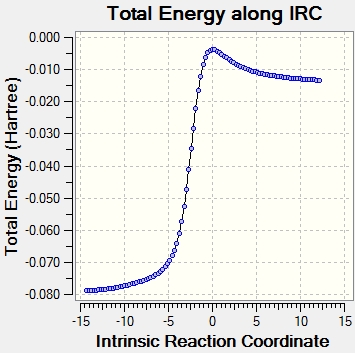
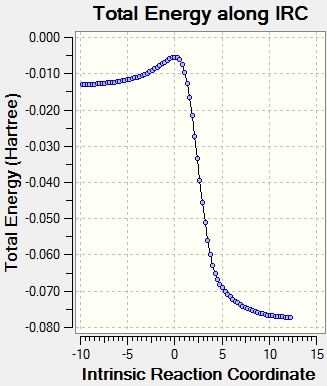
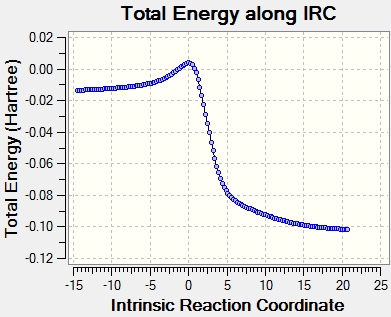
Intrinsic Reaction Coordinate

Reaction	Type of product	IRC	Total energy along IRC
Diels-Alder	Exo
Backward Diels-Alder Pathway of the formation of Exo product.
Diels-Alder	Endo
Forward Diels-Alder Pathway of the formation of Endo product.
Cheletropic
Forward cheletropic reaction.
Figure 9. The IRC and total energy along IRC of the DA and cheletropic reaction.

Energies

Sum of electronic and thermal free energies (Hartree)						Energy barrier (kJ/mol)	Reaction energies (kJ/mol)
	Xylylene	SO2	Reactants	TS	Product
Exo DA	0.178922	-0.119269	0.059653	0.092075	0.021452	85.12	-100.30
Endo DA	0.178922	-0.119269	0.059653	0.090557	0.021704	81.14	-99.64
Cheletropic	0.178922	-0.119269	0.059653	0.099062	0.000005	103.47	-156.61
Table 3: Values of the sum of electronic and thermal Free Energies (calculation ran at PM6)

For the DA reaction, the exo product is lower in energy than the endo product and makes it thermodynamically more stable. However, exo DA reaction has a higher energy barrier than endo DA reaction. Hence, endo DA reaction is kinetically favourable. The lowered energy barrier due to the secondary orbital interaction between the p-orbital of xylylene and p-orbitals from oxygen atoms on SO₂, and the slight difference of energy levels between exo and endo product suggest that endo DA reaction is the major pathway leading to the formation of product. In between the DA and cheletropic reaction, DA reaction is preferred at low temperature whereas cheletropic reaction is favourable at high temperature. At high temperature, cheletropic reactants gain enough thermal energy to overcome the higher energy barrier compares to DA reaction. Cheletropic product is much more stable than both the DA products due to its low energy level.

Xylylene is highly unstable due to its high Gibbs free energy. However, the energy level drops dramatically after the bonding of the 6-membered ring due to the delocalization of pi electrons around the aromatic system based on the IRC in figure 9.

Reaction profile

Figure 10. The reaction profile of the DA and cheletropic reaction.

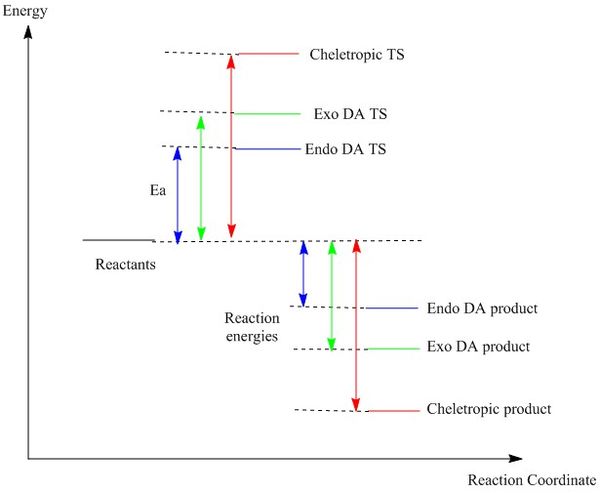
(It's useful to have values on the diagram for comparison Tam10 (talk) 13:00, 7 February 2017 (UTC))

Conclusion

By using Gaussview, the MOs of the HOMO and LUMO of different compounds can be generated. Both the HOMO and LUMO of a compound must have the same symmetry in order to react and hence has a non-zero overlap integral. In exercise 1, the bond lengths between the carbon atoms in reactants, TS and products were measured along the progress of DA reaction. The bond length of the carbon atoms between butadiene and ethene in TS is shorter than expected Van der Waals radius (3.4 Å) due to the approach of the reactants to each other which leads to the formation of two single bonds. In a classic DA reaction, 3 double bonds elongate to form single bonds and 1 single bond shortens to give double bond. The imaginary frequency in the vibration of TS shows the approach of both the reactants to undergo the pericyclic DA reaction.

From exercise 2, it is important to note that secondary orbital interaction and steric reasons can affect the kinetic and thermodynamic properties of the reaction, particularly the energies. Endo product is preferred in the reaction of Cyclohexadiene and 1,3-Dioxole based on the calculated energy barrrier and reaction energies. It is also an inverse electron demand reaction where the HOMO of dienophile is closer in energy with respect to the LUMO of diene than the HOMO of diene with LUMO of dienophile.

Xylylene and SO₂ can react via DA or cheletropic reaction. Based on the calculation of energy barrier and reaction energies, cheletropic reaction is preferred at high temperature where the reactants gain enough energy to overcome the high activation energy. Cheletropic product is much more stable than DA product once it is formed. For DA reaction, endo product is favoured over exo product after taking into consideration the secondary orbital interaction which lowers the energy barrier.