Optimisation

3-21G optimisation of BH₃ Molecule

Link to BH₃ 3-21G Optimisation .LOG file: click here

For JMol File:

Optimal Bond Distance: 1.19 Å

Optimal Bond Angle: 120.0°

BH₃ optimization results summary table:

Table 1
BH3 optimisation
File Name	bh3_opt
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	3-21G
Charge	0
Spin	Singlet
E(RB3LYP)	-26.46226338	a.u.
RMS Gradient Norm	0.00020672	a.u.
Imaginary Freq
Dipole Moment	0	Debye
Point Group	D3H
Job cpu time: 57.0 seconds

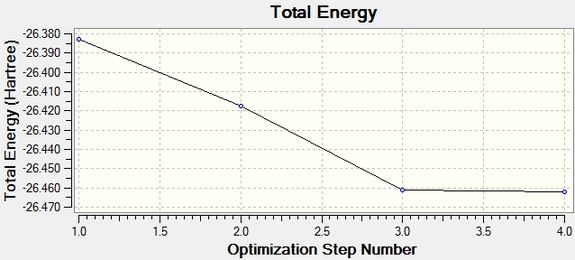
Calculation Log: 'Item' table of converged forces and distances for 3-21G BH₃ optimisation:

        Item               Value     Threshold  Converged?
 Maximum Force            0.000413     0.000450     YES
 RMS     Force            0.000271     0.000300     YES
 Maximum Displacement     0.001610     0.001800     YES
 RMS     Displacement     0.001054     0.001200     YES
 Predicted change in Energy=-1.071764D-06
 Optimization completed.
    -- Stationary point found.

Intermediate geometry optimisation plots:


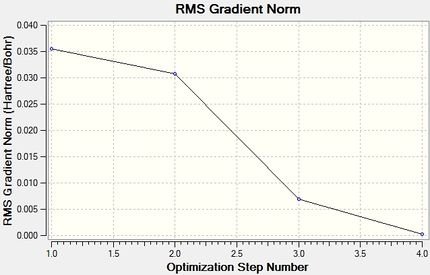Optimisation Plot: Total Energy	Optimisation Plot: RMS Gradient

Total Energy Minimum Value for 3-21G optimisation of BH₃ Molecule: -26.46226338 a.u.

631G(d,p) optimisation of BH₃ Molecule

Link to BH₃ 631G(d,p) optimisation .LOG file: click here

For JMol File:

Optimal Bond Distance: 1.19 Å

Optimal Bond Angle: 120.0°

BH₃ 631G(d,p) Optimization results summary table:

Table 2
BH3 optimisation
File Name	BH3_OPT_631G_DP
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-26.61532374	a.u.
RMS Gradient Norm	0.00000236	a.u.
Imaginary Freq
Dipole Moment	0	Debye
Point Group	CS
Job cpu time: 28.0 seconds

Calculation Log: 'Item' table of converged forces and distances for 6-31G(d,p) BH₃ optimisation:

         Item               Value     Threshold  Converged?
 Maximum Force            0.000005     0.000450     YES
 RMS     Force            0.000003     0.000300     YES
 Maximum Displacement     0.000020     0.001800     YES
 RMS     Displacement     0.000012     0.001200     YES
 Predicted change in Energy=-1.312911D-10
 Optimization completed.
    -- Stationary point found.

Intermediate geometry optimisation plots:


Optimisation Plot: Total Energy	Optimisation Plot: RMS Gradient

Total Energy Minimum Value for 631G(d,p) optimisation of BH₃ Molecule: -26.61532374 a.u.

LanL2DZ optimisation of TlBr₃ Molecule

Link to TlBr₃ LanL2DZ Optimisation Calculation on D-Space: DOI:10042/20468

Optimal Bond Distance: 2.65 Å

Literature value for TlBr bond distance: 2.481 Å ^[1]

Optimal Bond Angle: 120.0°

TlBr₃ LanL2DZ optimization results summary table:

Table 3
TlBr3 optimisation
File Name	TlBr3_OPT_LanL2DZ
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	LANL2DZ
Charge	0
Spin	Singlet
E(RB3LYP)	-91.21812851	a.u.
RMS Gradient Norm	0.0000009	a.u.
Imaginary Freq
Dipole Moment	0	Debye
Point Group	D3H
Job cpu time: 19.6 seconds

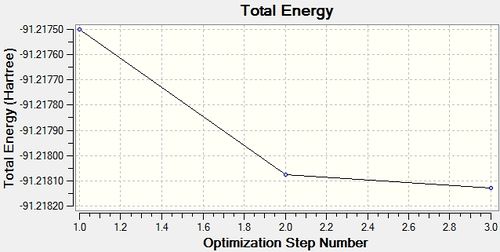
Calculation Log: 'Item' table of converged forces and distances for LanL2DZ TlBr₃ optimisation:

         Item               Value     Threshold  Converged?
 Maximum Force            0.000002     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000022     0.001800     YES
 RMS     Displacement     0.000014     0.001200     YES
 Predicted change in Energy=-6.084050D-11
 Optimization completed.
    -- Stationary point found.

Intermediate geometry optimisation plots:


Optimisation Plot: Total Energy	Optimisation Plot: RMS Gradient

Total Energy Minimum Value for LanL2DZ optimisation of TlBr₃ Molecule: -91.21812851 a.u.

GEN optimisation of BBr₃ Molecule

Link to BBr₃ GEN optimisation .LOG file: click here

Optimal Bond Distance: 1.93 Å

Optimal Bond Angle: 120.0°

BBr₃ optimization results summary table:

Table 4
BBr3 GEN Optimisation
File Name	BBR3_OPT_GEN
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	Gen
Charge	0
Spin	Singlet
E(RB3LYP)	-64.43645277	a.u.
RMS Gradient Norm	0.00000384	a.u.
Imaginary Freq
Dipole Moment	0.0002	Debye
Point Group	C2V
Job cpu time: 1 minutes 20.0 seconds

Calculation Log: 'Item' table of converged forces and distances for GEN BBr₃ optimisation:

          Item               Value     Threshold  Converged?
 Maximum Force            0.000008     0.000450     YES
 RMS     Force            0.000005     0.000300     YES
 Maximum Displacement     0.000036     0.001800     YES
 RMS     Displacement     0.000024     0.001200     YES
 Predicted change in Energy=-4.098477D-10
 Optimization completed.
    -- Stationary point found.

Intermediate geometry optimisation plots:


Optimisation Plot: Total Energy	Optimisation Plot: RMS Gradient

Total Energy Minimum Value for GEN optimisation of BBr₃ Molecule: -64.43645277 a.u.

Comparing and Contrasting the bond distances of BH₃, BBr₃ and TlBr₃

Table summarising the bond lengths of BH₃, BBr₃ and TlBr₃ calculated by Gaussian:

Table 5
Bond	Computated Bond Length (Å)
BH₃	1.19
BBr₃	1.93
TlBr₃	2.65

A chemical bond represents the build up of electron density between separate atoms to form a molecule. Depending on the size and shape of the orbitals, this interaction can be strong (leading to short bond lengths) or can be weak (leading to longer bond lengths).

As you can see the immediate trend is that moving from BH₃ to TlBr₃ the bond length is increasing. This trend can be understood by considering the relative sizes of the orbitals involved in bonding. If we first take BH₃ we see that Boron is in group 3 and row 2 meaning in size it has a comparatively small valence electron shell and thus a small electron radius. Now if we consider that the boron atom is bonding to Hydrogen we can understand why the bond length is so short, since hydrogen has one of the smallest electron radii being the first atom in the periodic table.

If we now consider BBr₃ we still have the boron atom but now have three Bromine atoms bonding to it. Bromine is in the fourth row of the periodic table and thus it's valence electrons extend out much further from the nucleus of the atom meaning it has a larger atomic radius than Hydrogen. In terms of bonding this results in a longer observed bond than in BH₃.

Finally if we consider TlBr₃ we can see that we have changed the central atom from Boron to Thallium. The bonding observed stays the same since Boron and Thallium are both in group three, however with Thallium in the sixth row of the periodic table, it's valence electrons are even further from the nucleus than in Bromine. This results in the longest bond length since the two orbitals interacting are the largest in size.

In some structures we sometimes observe a bond forming where we do not expect and this can also be explained by considering the orbital interactions of the atoms in the molecule. Unless sufficient electron density can build up between two atoms i.e. a strong orbital overlap, then a chemical bond will not form. Within Gaussian the output may show that a bond has not formed between two atoms, however this does not mean one does not exist. This is due to the fact that Gaussian only considers a bond to have formed when it conforms to a specific length criteria, however in inorganic bonding these lengths may exceed this value due to large orbital overlap.

Frequency Analysis

631G(d,p) frequency Analysis of BH₃ Molecule

Link to BH₃ 631G(d,p) frequency Analysis .LOG file: click here

Optimal Bond Distance: 1.19 Å

Optimal Bond Angle: 120.0

BH₃ 631G(d,p) Frequency analysis results summary table:

Table 6
BH3 Frequency
File Name	MICHAELSTANLEY_BH3_FREQ
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-26.61532374	a.u.
RMS Gradient Norm	0.00000237	a.u.
Imaginary Freq	0
Dipole Moment	0	Debye
Point Group	C2V
Job cpu time: 24.0 seconds

Calculation Log: 'Item' table of converged forces and distances for 631G(d,p) Frequency Analysis of BH₃:

         Item               Value     Threshold  Converged?
 Maximum Force            0.000005     0.000450     YES
 RMS     Force            0.000002     0.000300     YES
 Maximum Displacement     0.000020     0.001800     YES
 RMS     Displacement     0.000009     0.001200     YES
 Predicted change in Energy=-1.329322D-10
 Optimization completed.
    -- Stationary point found.

Low Frequencies:

Low frequencies ---  -18.6669   -0.0007   -0.0001    0.0008   12.5167   12.5631
 Low frequencies --- 1162.9785 1213.1756 1213.2363

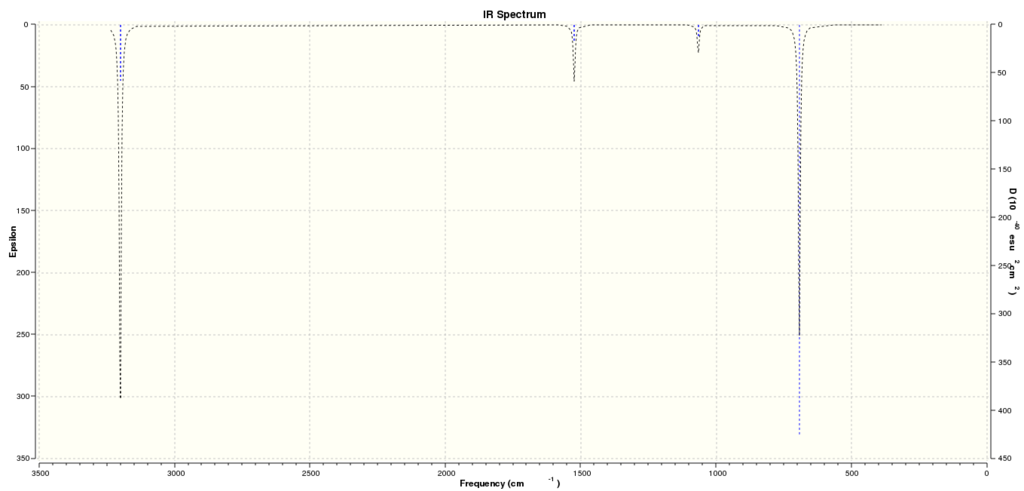
Table summarizing the computed vibrations of the BH3 molecule:

Computed IR SPectrum for BH₃:

Summary table of the vibrational frequencies of BH₃:

no.	Form of the vibration	Frequency	Intensity	Symmetry D_3h group
1	Wagging - All the hydrogen's move in and out of the plane of the molecule.	1162.98	92.55	A₂^"
2	Scissoring - Two of the hydrogen's move toward each other in a scissoring motion.	1213.18	14.06	E^'
3	Rocking - Two hydrogen's move in the same direction back and forth with the third moving in the opposite direction.	1213.24	14.06	E^'
4	Symmetric Stretch - All hydrogen's move back and forth in the plane of the molecule.	2582.26	0.00	A₁^'
5	Asymmetric Stretch - Two hydrogen's move back and forth out of time in the plane of the molecule.	2715.41	126.33	E^'
6	Asymmetric Stretch - All hydrogen's move back and forth in the plane of the molecule, two in time, one out of time.	2715.44	126.32	E^'

Question: Why are there less than six peaks in the spectrum, when there are obviously six vibrations?

Answer: Out of the six vibrations only five are IR active and thus observed. This is because the Symmetric stretch mode has no overall change in dipole moment. This can be confirmed by the calculated intensity value of 0.00 in the table above.

LanL2DZ frequency Analysis of TlBr₃ Molecule

For JMol File:

Link to TlBr₃ LanL2DZ Frequency Analysis on D-Space: DOI:10042/20504 Optimal Bond Distance: 2.65 Å

Optimal Bond Angle: 120°

TlBr₃ LanL2DZ Frequency analysis results summary table:

Table 7
TlBr3 Frequency
File Name	TlBr3_FREQ_LanL2DZ
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	LANL2DZ
Charge	0
Spin	Singlet
E(RB3LYP)	-91.21812851	a.u.
RMS Gradient Norm	0.00000088	a.u.
Imaginary Freq	0
Dipole Moment	0	Debye
Point Group	D3H
Job cpu time: 18.7 seconds

Calculation Log: 'Item' table of converged forces and distances for Frequency Analysis of TlBr₃:

         Item               Value     Threshold  Converged?
 Maximum Force            0.000002     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000022     0.001800     YES
 RMS     Displacement     0.000011     0.001200     YES
 Predicted change in Energy=-5.660901D-11
 Optimization completed.
    -- Stationary point found.

Low Frequencies:

 Low frequencies ---   -3.4213   -0.0026   -0.0004    0.0015    3.9367    3.9367
 Low frequencies ---   46.4289   46.4292   52.1449

Computed IR SPectrum for TlBr₃:

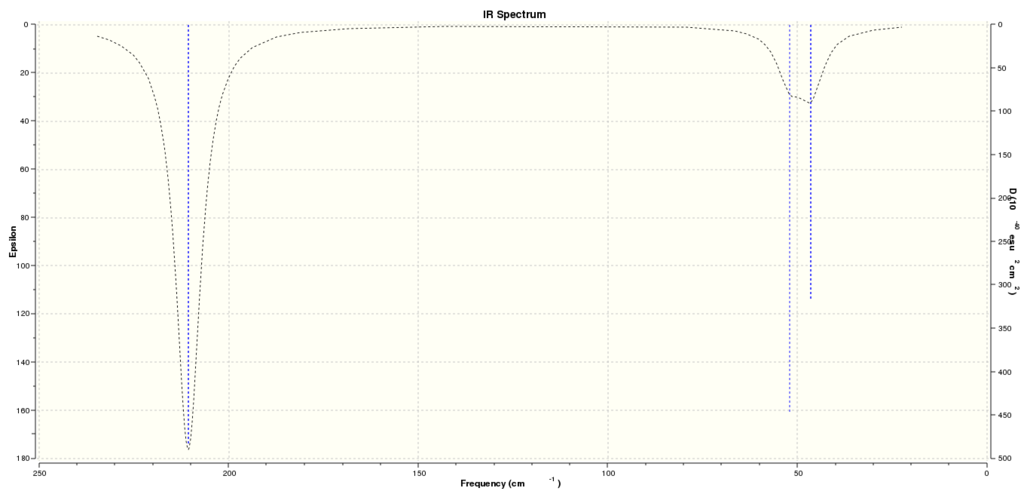
Summary table of the vibrational frequencies of TlBr₃:

no.	Form of the vibration	Frequency	Intensity	Symmetry D_3h group
1	Scissoring - Two of the H's move toward each other in a scissoring motion.	46.43	3.69	E^'
2	Rocking - Two H's move in the same direction back and forth with the third moving in the opposite direction.	46.43	3.69	E^'
3	Wagging - The Tl atom moves into the plane of the molecule and all the hydrogen's move out.	52.14	5.85	A₂^"
4	Symmetric Stretch - All H's move back and forth in the plane of the molecule.	165.27	0.00	A₁^'
5	Asymmetric Stretch - Two H's move back and forth out of time in the plane of the molecule while the Tl atom moves back and forth.	210.69	25.48	E^'
6	Asymmetric Stretch - All H's move in and out of the plane of the molecule, two in time, one out. Tl atom moves opposite to the one H atom.	210.69	25.48	E^'

Comparing the vibrational frequencies of BH₃ and Tl₃:

Using the 3N-6 rule we can confirm that both BH₃ and Tl₃ exhibit six vibrational modes as calculated. Looking at the frequencies of the vibrations we see that they are at a much lower frequency in Tl₃ than in BH₃. This implies that the Tl-Br bond is much weaker than the B-H bond. If we look at the Tl-Br bond length we see that it is longer than the B-H bond length thus suggesting that the bonds in Tl₃ are much weaker.

We can rationalise the observed bonding when we consider the relative orbitals involved. In BH₃ the bonds are 2s and 2p derived sp² hybridised orbitals bonding to 1s Hydrogen orbitals. In Tl₃ the bonding is derived from 6s and 6p orbitals and thus the orbitals are much more diffuse, thus resulting in poorer orbitals overlap and thus weaker bonds.

If we next consider the order of the vibrational modes for BH₃ and Tl₃ we see that in BH₃ the wagging mode is the lowest frequency mode whereas in Tl₃ this is the scissoring mode. This reordering of modes can be rationalised when we consider that the bond lengths in Tl₃ are much longer, thus requiring more energy to move the bromine atoms.

These spectra are similar in the sense that there are two signals at a low and two at a high frequency. The A₂^' and E' and the A₁^' and E' respectively. This reason for this observation becomes clear when we inspect the form of the vibrations for A₂^' and E' and A₁^' and E'. Both A₂^' and E' involve only a change in bond angle and not bond length, thus these are low energy and thus low frequency vibrations. When we consider A₁^' and E' we see that these modes involve a change in bond length which is a much higher energy process, thus occurs at a higher frequency.

When conducting a frequency analysis there are two operations being carried out by the computer. The first is the calculation of the second derivative of the potential energy surface which allows us to determine whether we are looking at a transition state or a minimum. The second is the calculation of the vibrational modes of the molecules and this the IR and Raman spectra. This allows us to check whether the results obtained match up with experimental values.

When running an optimisation and frequency analysis on a molecule, we must ensure that the same method and basis sets are used for both calculations. The reason for this is it allows us to make comparisons between the two outputs from the calculations since the same method and basis set have been employed. When we get the output from the calculation we always check to make sure that the low frequencies reported are as close to zero as possible. The reason for this is because these low frequencies represent the vibrations of the centre of mass of the molecule (the -6 value in the 3N-6 formula) and thus will be very small compared the the other vibrations.

Molecular Orbitals

Molecular orbitals of BH₃

Link to BH₃ MO analysis on D-space: DOI:10042/20527

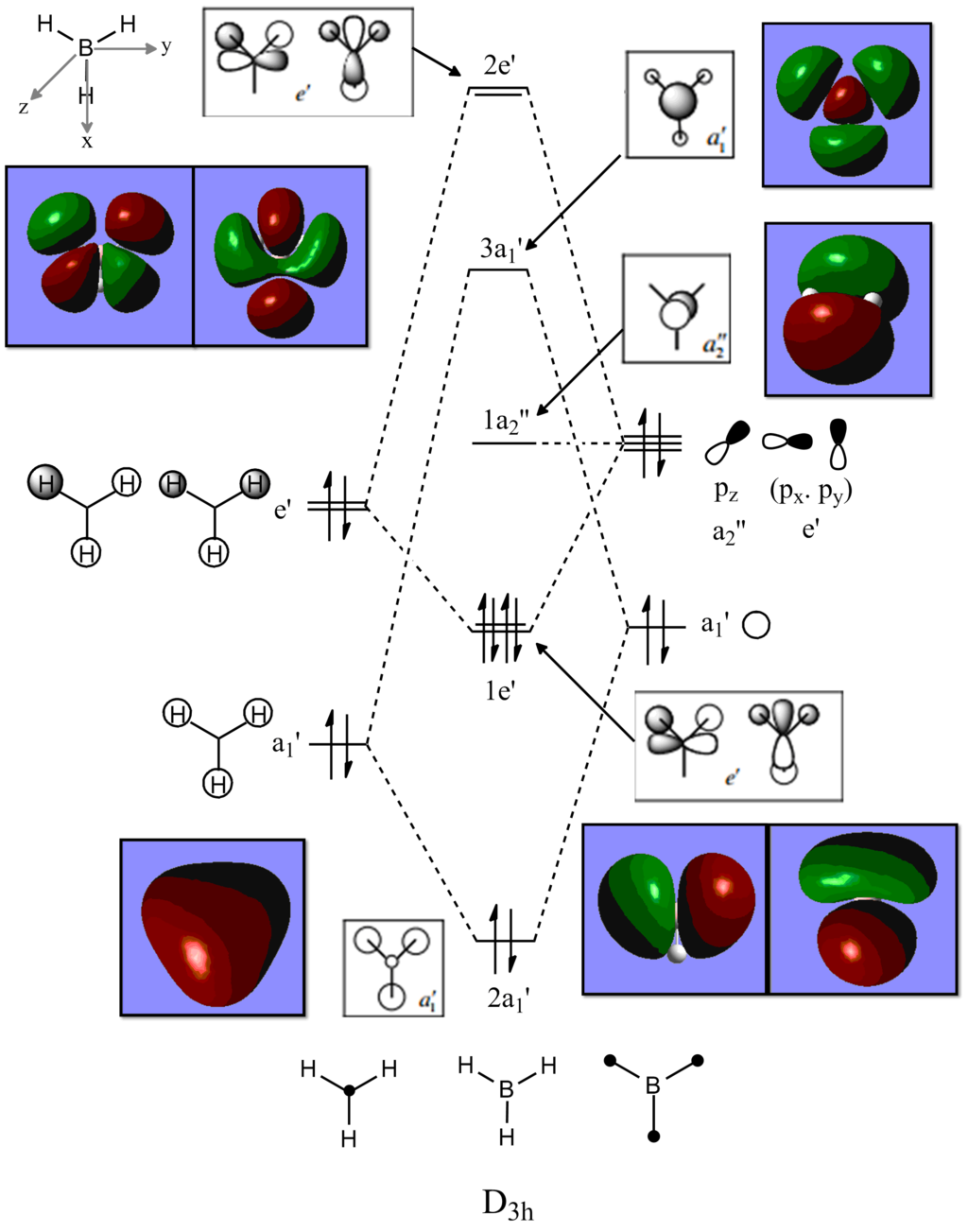
Black and White Molecular orbital diagrams obtained from: ^[2]

There are very little differences between the computed MO's and the real ones. This indicates that qualitative MO theory is very effective in predicting the energy levels and relative shapes of the molecular orbitals of simple molecules. This becomes very useful for predicting reactivity and HOMO-LUMO interactions.

NBO Analysis

631G(d,p) optimisation of NH₃

For JMol File:

Link to NH₃ 631G(d,p) optimisation on D-Space: DOI:10042/20526

Optimal Bond Distance: 1.02 Å

Optimal Bond Angle: 105.7°

NH₃ 631G(d,p) optimization results summary table:

Table 8
NH3 Optimisation
File Name	NH3_OPT_631G_dp
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-56.55776856	a.u.
RMS Gradient Norm	0.00000885	a.u.
Imaginary Freq
Dipole Moment	1.8464	Debye
Point Group	C1
Job cpu time: 20.9 seconds

Calculation Log: 'Item' table of converged forces and distances for 631G(d,p) optimisation of NH₃:

         Item               Value     Threshold  Converged?
 Maximum Force            0.000024     0.000450     YES
 RMS     Force            0.000012     0.000300     YES
 Maximum Displacement     0.000079     0.001800     YES
 RMS     Displacement     0.000053     0.001200     YES
 Predicted change in Energy=-1.629727D-09
 Optimization completed.
    -- Stationary point found.

Intermediate geometry optimisation plots:


Optimisation Plot: Total Energy	Optimisation Plot: RMS Gradient

Total Energy Minimum Value for 631G(d,p) optimisation of NH₃ Molecule: -56.55776856 a.u.

631G(d,p) frequency Analysis of NH₃

For JMol File:

Link to NH₃ 631G(d,p) frequency analysis on D-Space: DOI:10042/20528

Optimal Bond Distance: 1.02 Å

Optimal Bond Angle: 105.7°

NH3 631G(d,p) frequency analsyis results summary table:

Table 9
NH3 Freq
File Name	NH3_FREQ_631G_dp
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-56.55776856	a.u.
RMS Gradient Norm	0.00000878	a.u.
Imaginary Freq	0
Dipole Moment	1.8464	Debye
Point Group	C1
Job cpu time: 14.2 seconds

Calculation Log: 'Item' table of converged forces and distances for Frequency Analysis of NH₃:

         Item               Value     Threshold  Converged?
 Maximum Force            0.000021     0.000450     YES
 RMS     Force            0.000009     0.000300     YES
 Maximum Displacement     0.000077     0.001800     YES
 RMS     Displacement     0.000039     0.001200     YES
 Predicted change in Energy=-1.592773D-09
 Optimization completed.
    -- Stationary point found.

Low Frequencies:

Low frequencies ---  -30.8045   -0.0015   -0.0013    0.0008   20.2188   28.2150
 Low frequencies --- 1089.5530 1694.1235 1694.1861

Computed IR Spectrum for NH₃:

631G(d,p) NBO analysis of NH₃

Link to NH₃ 631G(d,p) energy calculation on D-space: DOI:10042/20529

Charge Distribution of NH₃ molecule:

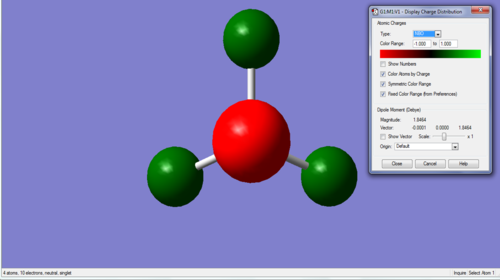
Charge range -1.0 - +1.0

Specific charges on atoms: N = -1.125, H = +0.375

Association energies: Ammonia-Borane

631G(d,p) optimisation of NH₃BH₃

For JMol File:

Link to NH₃BH₃ 631G(d,p) optimisation on D-Space: DOI:10042/20539

Optimal N-B Bond Distance: 1.67 Å

Optimal Bond Angle: N-B-H ≈ 104.6°, B-N-H ≈ 111.0°

NH₃BH₃ 631G(d,p) optimization results summary table:

Table 10
NH3BH3 Optimisation
File Name	NH3_BH3_OPT_631G_dp
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-83.22469002	a.u.
RMS Gradient Norm	0.00006847	a.u.
Imaginary Freq
Dipole Moment	5.5654	Debye
Point Group	C1
Job cpu time: 1 minutes 26.2 seconds

Calculation Log: 'Item' table of converged forces and distances for Frequency Analysis of NH₃BH₃:

         Item               Value     Threshold  Converged?
 Maximum Force            0.000139     0.000450     YES
 RMS     Force            0.000063     0.000300     YES
 Maximum Displacement     0.000761     0.001800     YES
 RMS     Displacement     0.000339     0.001200     YES
 Predicted change in Energy=-2.028975D-07
 Optimization completed.
    -- Stationary point found.

Intermediate geometry optimisation plots:


Optimisation Plot: Total Energy	Optimisation Plot: RMS Gradient

Total Energy Minimum Value for 631G(d,p) optimisation of NH₃BH₃ Molecule: -83.22469002 a.u.

631G(d,p) frequency analysis of NH₃BH₃

For JMol File:

Link to NH₃BH₃ 631G(d,p) frequency analysis on D-Space: DOI:10042/20541

Optimal Bond Distance: 1.67 Å

Optimal Bond Angle: N-B-H ≈ 104.6°, B-N-H ≈ 111.0°

NH₃BH₃ frequency analsyis results summary table:

Table 11
NH3BH3 Frequency
File Name	NH3_BH3_FREQ_631G_dp
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-83.22469006	a.u.
RMS Gradient Norm	0.00006851	a.u.
Imaginary Freq	0
Dipole Moment	5.5654	Debye
Point Group	C1
Job cpu time: 56.5 seconds

Calculation Log: 'Item' table of converged forces and distances for Frequency Analysis of NH₃BH₃:

         Item               Value     Threshold  Converged?
 Maximum Force            0.000127     0.000450     YES
 RMS     Force            0.000069     0.000300     YES
 Maximum Displacement     0.000801     0.001800     YES
 RMS     Displacement     0.000532     0.001200     YES
 Predicted change in Energy=-2.128467D-07
 Optimization completed.
    -- Stationary point found.

Low frequencies:

Low frequencies ---   -0.0012   -0.0010    0.0009   19.0734   23.7378   42.9981
 Low frequencies ---  266.5957  632.3884  639.5018

Computed IR Spectrum for NH₃BH₃:

Association Energies:

E(NH₃)= -56.55776856 a.u. E(BH₃)= -26.61532374 a.u. E(NH₃BH₃)= -83.22469006 a.u.

ΔE=E(NH3BH3)-[E(NH3)+E(BH3)]

ΔE= -83.22469006 - (-56.55776856-26.61532374)= -83.22469006 + 83.1730923 = -0.0515983 a.u.

ΔE= -0.0515983 a.u. x 2625.50 KJ.mol^-1.au^-1 ^[3] = -135.47 (+/-10) KJ.mol^-1

This is the value of the dissociation energy for the N-B bond and thus the association energy is simply: ΔE_{Association = +135.47 (+/-10) KJ.mol^-1}

This value is in very good agreement with the literature value of +130 KJ.mol^-1 ^[4].

Mini Project

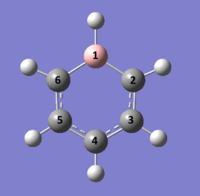
Benzene

631G(d,p) optimisation of Benzene

For JMol File:

Link to Benzene 631G(d,p) optimisation on D-Space: DOI:10042/20616

Optimal Bond Distance: 1.40 Å

Optimal Bond Angle: 120.0°

Benzene 631G(d,p) optimization results summary table:

Benzene Optimisation
File Name	MS_Benzene_OPT_631Gdp
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-232.2582055	a.u.
RMS Gradient Norm	0.00009549	a.u.
Imaginary Freq
Dipole Moment	0.0001	Debye
Point Group	C1
Job cpu time: 1 minutes 25.4 seconds

Calculation Log: 'Item' table of converged forces and distances for optimisation of Benzene:

         Item               Value     Threshold  Converged?
 Maximum Force            0.000212     0.000450     YES
 RMS     Force            0.000085     0.000300     YES
 Maximum Displacement     0.000991     0.001800     YES
 RMS     Displacement     0.000315     0.001200     YES
 Predicted change in Energy=-5.157405D-07
 Optimization completed.
    -- Stationary point found.

Intermediate geometry optimisation plots:


Optimisation plot of Benzene - Total energy	Optimisation plot of Benzene - RMS Gradient Norm

Total Energy Minimum Value for 631G(d,p) optimisation of Benzene Molecule: -232.2582055 a.u

631G(d,p) frequency analysis of Benzene

For JMol File:

Link to Benzene 631G(d,p) frequency analysis on D-Space: DOI:10042/20641

Optimal Bond Distance: 1.40 Å

Optimal Bond Angle: 120.0 °

Benzene 631G(d,p) frequency analsyis results summary table:

Benzene Optimisation
File Name	MS_Benzene_FREQ_631Gdp
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-232.25820533	a.u.
RMS Gradient Norm	0.00009549	a.u.
Imaginary Freq
Dipole Moment	0.0001	Debye
Point Group	C1
Job cpu time: 4 minutes 40.1 seconds

Calculation Log: 'Item' table of converged forces and distances for frequency analysis of Benzene:

         Item               Value     Threshold  Converged?
 Maximum Force            0.000195     0.000450     YES
 RMS     Force            0.000095     0.000300     YES
 Maximum Displacement     0.001065     0.001800     YES
 RMS     Displacement     0.000381     0.001200     YES
 Predicted change in Energy=-5.069198D-07
 Optimization completed.
    -- Stationary point found.

Low frequencies:

Low frequencies ---  -17.3954  -14.6988   -9.7872   -0.0003    0.0005    0.0006
 Low frequencies ---  413.7961  414.4656  620.8509

Computed IR Spectrum for Benzene:

MO analysis of Benzene

Link to MO and NBO analysis on D-Space: DOI:10042/20649

MO Diagram for Benzene: Pi Orbitals Only:

Black and White Molecular orbital diagrams obtained from: ^[5]

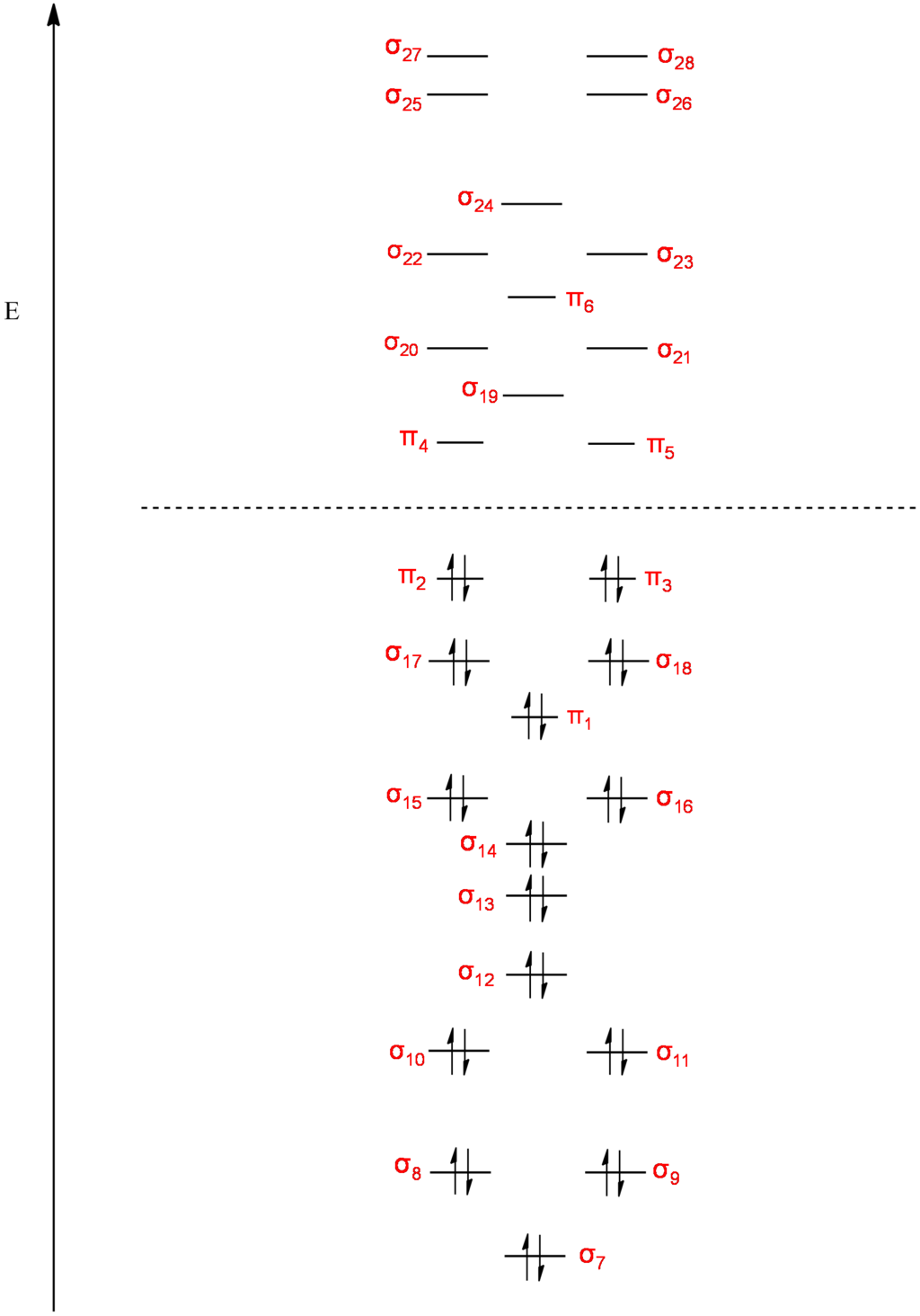
MO Diagram for Benzene: Sigma and Pi orbitals (Orbital pictures follow):

Molecular Orbitals of Benzene: Pi and Sigma:

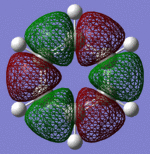
Sigma Orbital 7	Sigma Orbital 8	Sigma Orbital 9	Sigma Orbital 10

Sigma Orbital 11	Sigma Orbital 12	Sigma Orbital 13	Sigma Orbital 14

Sigma Orbital 15	Sigma Orbital 16	Pi Orbital 17	Sigma Orbital 18

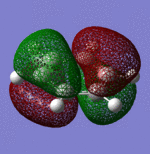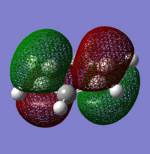Sigma Orbital 19	Pi Orbital 20	Pi Orbital 21	Pi Orbital 22

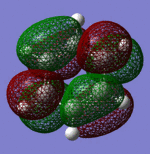Pi Orbital 23	Sigma Orbital 24	Sigma Orbital 25	Sigma Orbital 26

Pi Orbital 27	Sigma Orbital 28	Sigma Orbital 29	Sigma Orbital 30

Sigma Orbital 31	Sigma Orbital 32	Sigma Orbital 33	Sigma Orbital 34

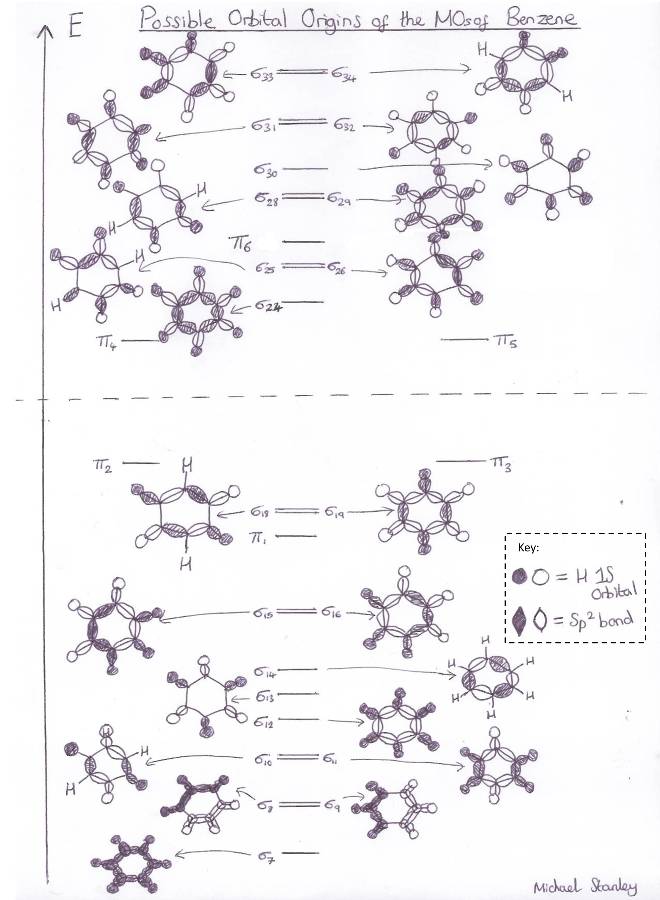
From inspection of the molecular orbitals calculated by Gaussian we can make a guess as to the AO's that were combined to make them. Obviously the Pi symmetry orbitals are Pi in origin however guessing as to the origin of the sigma orbitals becomes quite difficult. Below is an MO diagram I have constructed which displays what I believe to be the atomic orbitals responsible for the sigma MO's in Benzene:

NBO analysis of Benzene

Link to NBO analysis on D-Space: DOI:10042/20649

Charge Distribution of Benzene molecule:

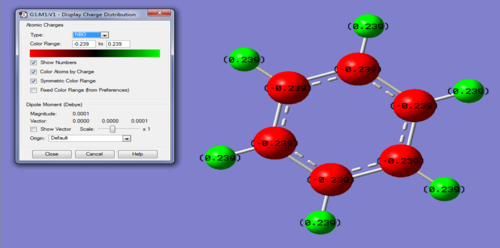
Charge range: -0.239 - 0.239

Specific charges on atoms: C = -0.239, H = 0.239

Boratabenzene

631G(d,p) optimisation of Boratabenzene

For JMol File:

Link to Boratabenzene 631G(d,p) optimisation on D-Space: DOI:10042/20800

Optimal Bond Distances: B1-C2 = 1.51 Å, C2-C3 = 1.40 Å, C3-C4 = 1.41 Å, C4-C5 = 1.41 Å, C5-C6 = 1.40 Å, C6-B1 = 1.51 Å.

Optimal Bond Angle: C6-B1-C1 = 115.11°

Boratabenzene 631G(d,p) optimization results summary table:

Boratabenzene_Optimisation
File Name	MS_Boratabenzene_OPT_631Gdp
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	-1
Spin	Singlet
E(RB3LYP)	-219.0205299	a.u.
RMS Gradient Norm	0.00015729	a.u.
Imaginary Freq
Dipole Moment	2.8465	Debye
Point Group	C1
Job cpu time: 3 minutes 2.4 seconds

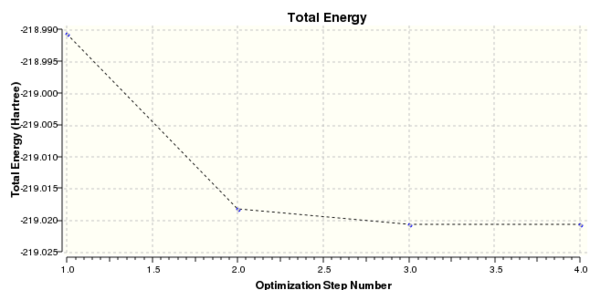
Calculation Log: 'Item' table of converged forces and distances for optimisation of Boratabenzene:

         Item               Value     Threshold  Converged?
 Maximum Force            0.000159     0.000450     YES
 RMS     Force            0.000068     0.000300     YES
 Maximum Displacement     0.000888     0.001800     YES
 RMS     Displacement     0.000326     0.001200     YES
 Predicted change in Energy=-6.533587D-07
 Optimization completed.
    -- Stationary point found.

Total Energy Minimum Value for 631G(d,p) optimisation of Boratabenzene Molecule: -219.0205299 a.u.

631G(d,p) frequency analysis of Boratabenzene

For JMol File:

Link to Boratabenzene 631G(d,p) frequency analysis on D-Space: DOI:10042/20642

Boratabenzene 631G(d,p) frequency analysis results summary table:

Boratabenzene_Frequency
File Name	MS_Boratabenzene_FREQ_631Gdp
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	-1
Spin	Singlet
E(RB3LYP)	-219.0205299	a.u.
RMS Gradient Norm	0.00015726	a.u.
Imaginary Freq	0
Dipole Moment	2.8465	Debye
Point Group	C1
Job cpu time: 4 minutes 22.8 seconds

Calculation Log: 'Item' table of converged forces and distances for frequency analysis of Boratabenzene:

         Item               Value     Threshold  Converged?
 Maximum Force            0.000432     0.000450     YES
 RMS     Force            0.000157     0.000300     YES
 Maximum Displacement     0.000889     0.001800     YES
 RMS     Displacement     0.000394     0.001200     YES
 Predicted change in Energy=-7.120649D-07
 Optimization completed.
    -- Stationary point found.

Low Frequencies:

Low frequencies ---  -13.1286   -0.0008   -0.0007    0.0005   15.0635   18.1734
 Low frequencies ---  371.3453  404.2332  565.2514

Computed IR Spectrum for Boratabenzene:

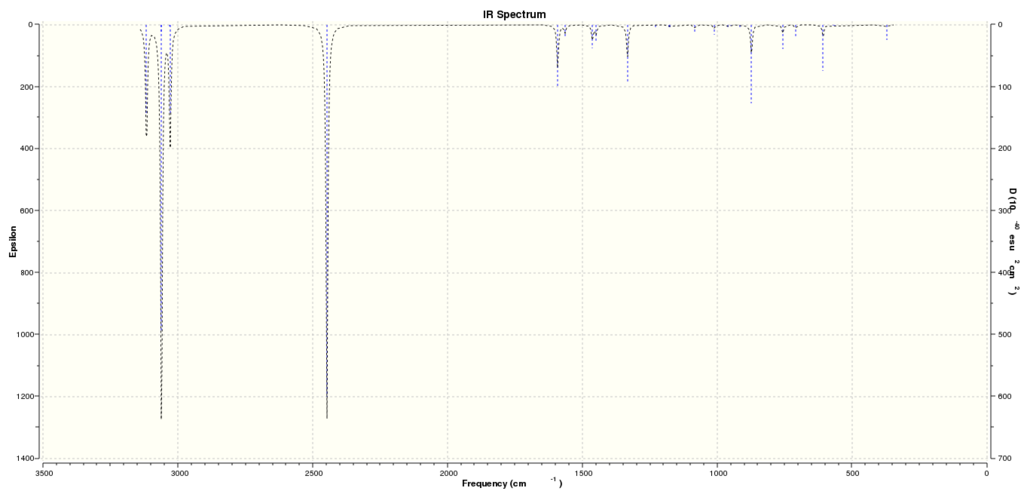
MO and NBO analysis of Boratabenzene

Link to Boratabenzene MO calculation on D-Space: DOI:10042/20876

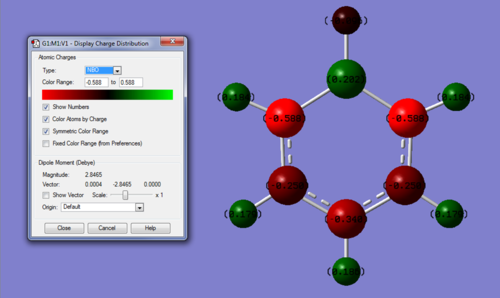
NBO analysis:

Charge range: -0.588 - +0.588

Specific charges on atoms: C(2,6) = -0.588, C(3,5) = -0.250, C(4) = -0.340, B = +0.202, H(1) = -0.096, H(2,6) = +0.184, H(3,5) = +0.179, H(4) = +0.186

Pyridinium

631G(d,p) optimisation of Pyridinium

For JMol File:

Link to Pyridinium 631G(d,p) optimisation on D-Space: DOI:10042/20801

Optimal Bond Distances: N1-C2 = 1.40 Å, C2-C3 = 1.39 Å, C3-C4 = 1.40 Å, C4-C5 = 1.39 Å, C5-C6 = 1.40 Å, C6-N1 = 1.39 Å.

Optimal Bond Angle: C6-N1-C1 = 120.0°

Pyridinium 631G(d,p) optimization results summary table:

Pyridinium_Optimisation
File Name	MS_Pyridinium_OPT_631Gdp
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	1
Spin	Singlet
E(RB3LYP)	-248.668074	a.u.
RMS Gradient Norm	0.0000391	a.u.
Imaginary Freq
Dipole Moment	1.8727	Debye
Point Group	C1
Job cpu time: 3 minutes 0.1 seconds

Calculation Log: 'Item' table of converged forces and distances for optimisation of Pyridinium:

         Item               Value     Threshold  Converged?
 Maximum Force            0.000064     0.000450     YES
 RMS     Force            0.000023     0.000300     YES
 Maximum Displacement     0.000822     0.001800     YES
 RMS     Displacement     0.000175     0.001200     YES
 Predicted change in Energy=-6.913998D-08
 Optimization completed.
    -- Stationary point found.

Intermediate geometry optimisation plots:


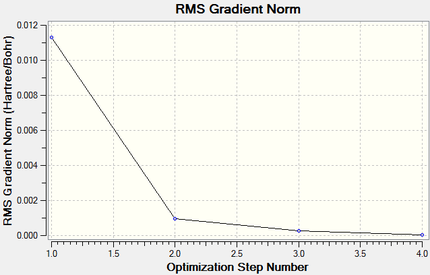Optimisation Plot: Total Energy	Optimisation Plot: RMS Gradient

Total Energy Minimum Value for 631G(d,p) optimisation of Pyridinium Molecule: -248.668074 a.u.

631G(d,p) frequency analysis of Pyridinium

For JMol File:

Link to Pyridinium 631G(d,p) frequency analysis on D-Space: DOI:10042/20802

Pyridinium 631G(d,p) frequency analysis results summary table:

Pyridinium_Frequency
File Name	MS_Pyridinium_FREQ_631Gdp
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	1
Spin	Singlet
E(RB3LYP)	-248.668074	a.u.
RMS Gradient Norm	0.00003905	a.u.
Imaginary Freq	0
Dipole Moment	1.8727	Debye
Point Group	C1
Job cpu time: 5 minutes 52.4 seconds

Calculation Log: 'Item' table of converged forces and distances for frequency analysis of Pyridinium:

         Item               Value     Threshold  Converged?
 Maximum Force            0.000155     0.000450     YES
 RMS     Force            0.000039     0.000300     YES
 Maximum Displacement     0.000775     0.001800     YES
 RMS     Displacement     0.000228     0.001200     YES
 Predicted change in Energy=-7.452539D-08
 Optimization completed.
    -- Stationary point found.

Low Frequencies:

Low frequencies ---   -7.2067   -0.0012   -0.0009   -0.0009   17.3396   18.5390
 Low frequencies ---  392.4558  404.0617  620.4714

Computed IR Spectrum for Pyridinium:

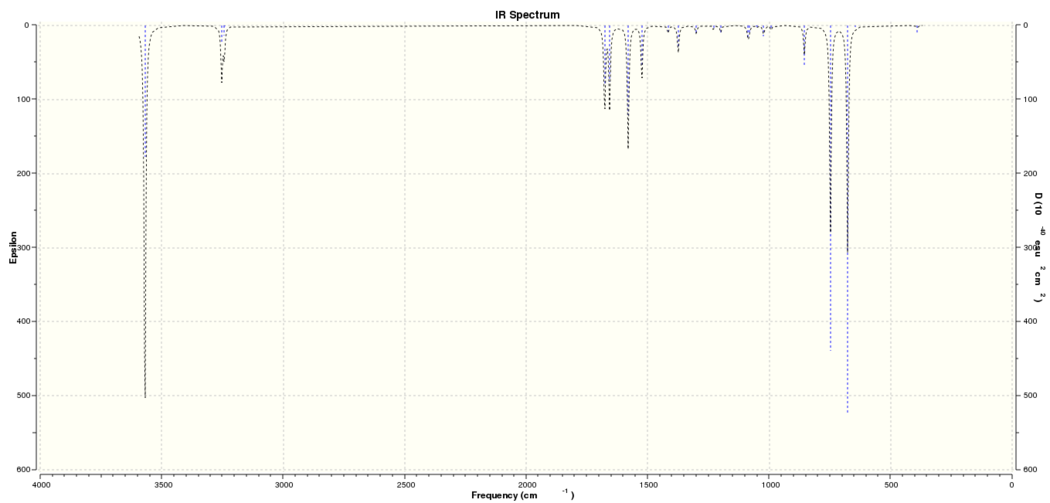
MO and NBO analysis of Pyridinium

Link to Pyridinium MO calculation on D-Space: DOI:10042/20878

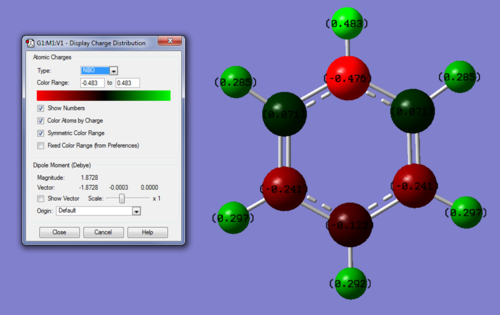
NBO anlaysis:

Charge range: -0.483 - +0.483

Specific charges on atoms: C(2,6) = +0.071, C(3,5) = -0.241, C(4) = -0.122, N = +0.202, H(1) = +0.483, H(2,6) = +0.285, H(3,5) = +0.297, H(4) = +0.292

Borazine

631G(d,p) optimisation of Borazine

For JMol File:

Link to Borazine 631G(d,p) optimisation on D-Space: DOI:10042/20827

Optimal Bond Distance: 1.39 Å

Optimal Bond Angle: 120.0°

Borazine 631G(d,p) optimization results summary table:

Borazine_Optimisation
File Name	MS_Borazine_OPT_631Gdp
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-242.6845975	a.u.
RMS Gradient Norm	0.00017356	a.u.
Imaginary Freq
Dipole Moment	0.0003	Debye
Point Group	C1
Job cpu time: 4 minutes 19.4 seconds

Calculation Log: 'Item' table of converged forces and distances for optimisation of Borazine:

         Item               Value     Threshold  Converged?
 Maximum Force            0.000176     0.000450     YES
 RMS     Force            0.000078     0.000300     YES
 Maximum Displacement     0.000758     0.001800     YES
 RMS     Displacement     0.000289     0.001200     YES
 Predicted change in Energy=-8.301264D-07
 Optimization completed.
    -- Stationary point found.

Intermediate geometry optimisation plots:


Optimisation Plot: Total Energy	Optimisation Plot: RMS Gradient

Total Energy Minimum Value for 631G(d,p) optimisation of Borazine Molecule: -242.6845975 a.u.

631G(d,p) frequency analysis of Borazine

For JMol File:

Link to Borazine 631G(d,p) frequency analysis on D-Space: DOI:10042/20828

Borazine 631G(d,p) frequency analysis results summary table:

Borazine_Frequency
File Name	MS_Borazine_FREQ_631Gdp
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-242.6845978	a.u.
RMS Gradient Norm	0.00017347	a.u.
Imaginary Freq	0
Dipole Moment	0.0003	Debye
Point Group	C1
Job cpu time: 5 minutes 38.8 seconds

Calculation Log: 'Item' table of converged forces and distances for frequency analysis of Borazine:

         Item               Value     Threshold  Converged?
 Maximum Force            0.000426     0.000450     YES
 RMS     Force            0.000173     0.000300     YES
 Maximum Displacement     0.000902     0.001800     YES
 RMS     Displacement     0.000402     0.001200     YES
 Predicted change in Energy=-9.360321D-07
 Optimization completed.
    -- Stationary point found.

Low Frequencies:

Low frequencies ---   -0.0005    0.0006    0.0014    7.2644    8.6683   11.4869
 Low frequencies ---  289.3474  289.9361  404.2566

Computed IR Spectrum for Borazine:

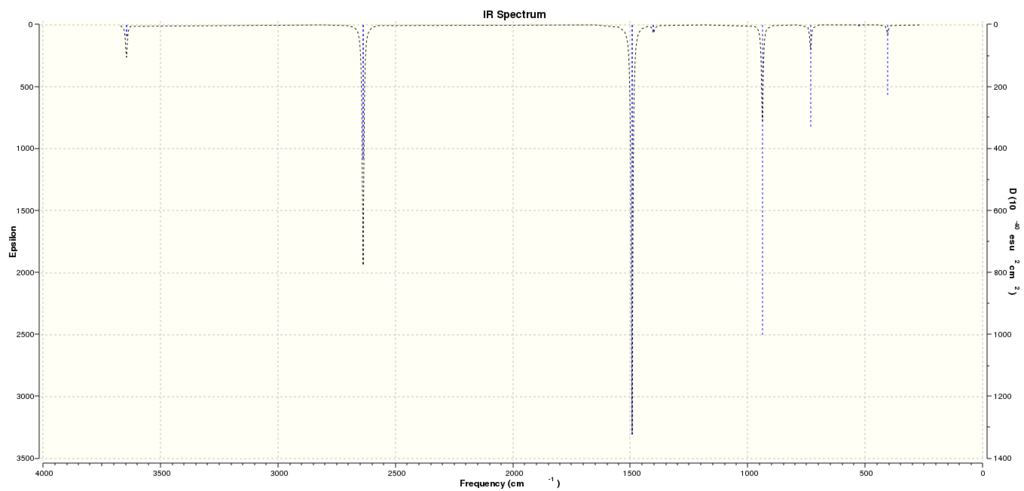
MO and NBO analysis of Borazine

Link to Borazine MO calculation on D-Space: DOI:10042/20877

NBO anlaysis:

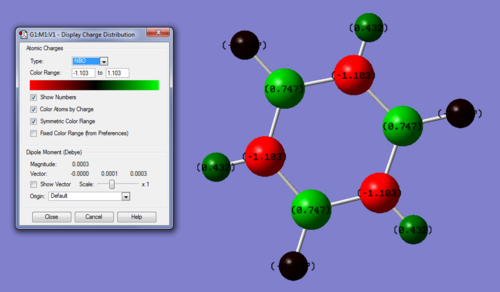
Charge range: -1.103 - +1.103

Specific charges on atoms: B = -1.103, N = +0.747, Boron Hydrogen's = +0.432, Nitrogen Hydorgen's = -0.077

Charge distribution and MO comparison

Charge distributions of Benzene, Boratobenzene, Pyridinium and Borazine:

Benzene	Boratobenzene	Pyridinium	Borazine

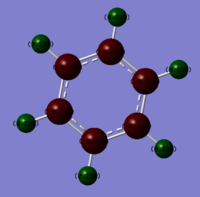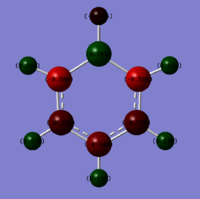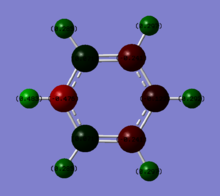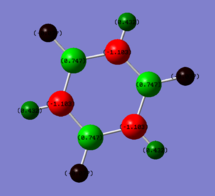
Charge range set to -1.0 and +1.0 for comparison.

For the MO comparison I decided to compare the Pi(1) totally bonding orbital, the Pi(2) and Pi(5) orbitals as these would be the most important orbitals in terms of reactivity and aromaticity:

Pi(1) totally bonding orbital

Benzene	Boratobenzene	Pyridinium	Borazine

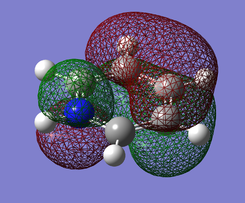
Pi(2) orbital

Benzene	Boratobenzene	Pyridinium	Borazine

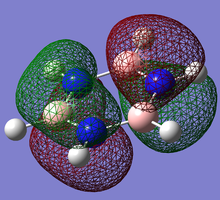
Pi(5) orbital

Benzene	Boratobenzene	Pyridinium	Borazine

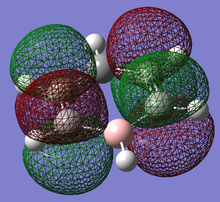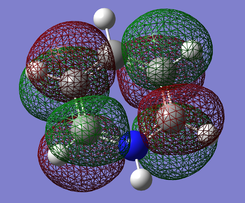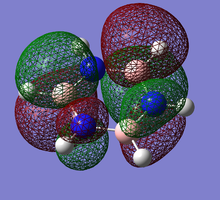
Discussion

When we consider the totally bonding Pi(1) orbitals for Benzene, Boratabenzene, Pyridinium and Borazine we do not see any marked differences. This is understandable since the molecular orbital is made up of a cyclic array of p-orbitals which do not differ greatly in Carbon, Boron and Nitrogen.

Moving to the Pi(2) orbitals we begin to see differences emerging. In Boratabenzene there is a much larger cloud of electrons around the boron atom than in Benzene and conversely there is a much smaller cloud around the Nitrogen atom in Pyridinium. If we consider that in Boratabenzene the Boron atom has a formal negative charge, this explains the increased concentration of electron density around this part of the molecule. In Pyridinium there is a formal positive charge on the Nitrogen atom and thus we can now understand why there is a low density of electrons around this part of the molecule. In Borazine we see less of a marked difference from Benzene largely due to the high symmetry of the molecule.

Finally if we consider the Pi(5) orbital we do not see much of a marked change upon moving from Benzene to Boratabenzene and Pyridinium, however we do see a change in the molecular orbital for Borazine. The relative size of the lobes in the Borazine Pi(5) orbitals are different from that of benzene. Instead of symmetrical orbitals we observe two sets of differently sized lobes on either side of the molecule.

Effects of the Substitution on the MO diagram for Benzene:

On going from Benzene to Boratabenzene we would observe an increase in energy of the LCAOs containing Boron orbitals that contribute to the MOs. This is because Boron is less electronegative than Carbon. As a result the energy of the bonding MO's would increase and the energy of the anti-bonding MO's would decrease. This is due to poor overlap of the LCAOs contributing to the MO's due to the change in energy. Due to the reduction in symmetry on going from Benzene to Boratabenzene we would expect there to be less degenerate MO's.

On going from Benzene to Pyridinium we would observe an decrease in energy of the LCAOs containing Nitrogen orbitals that contribute to the MOs. This is because Nitrogen is more electronegative than Carbon. As a result the energy of the bonding MO's would increase and the energy of the anti-bonding MO's would decrease. This is due to poor overlap of the LCAOs contributing to the MO's due to the change in energy. Due to the reduction in symmetry on going from Benzene to Pyridinium we would expect there to be less degenerate MO's.

On going from Benzene to Borazene we would expect to see a dramatic change in the relative energy levels of the MOs. This can be rationalised by the large difference in energy of the Nitrogen and Boron LCAOs that contribute to the overall MO and would result in poor orbital overlap between the LCAOs. We can expect to see much smaller splitting of the energy levels in the MO due to this orbital mismatch.

References

↑ J.Glaser, G.Johansson.On the Structures of the Hydrated Thallium(III) Ion and it's Bromide Complexes in Aqueous Solution. Department of Inorganic Chemistry, Royal Institute of Technology, Sweden. [Online] 1982: 125. Available from: http://actachemscand.dk/pdf/acta_vol_36a_p0125-0135.pdf [Accessed: 19th October 2012]
↑ Dr. Hunt, Hunt Research Group, Department of Chemistry, Imperial College London, BH3 Tutorial Problem [ONLINE]. Available from: http://www.huntresearchgroup.org.uk/teaching/teaching_comp_lab_year3/Tut_MO_diagram_BH3.pdf [Accessed 18th October 2012].
↑ Dr. Antonio Tilocca, Royal Society Uinversity Research Fellow, University College London, Main Energy conversion factors [ONLINE]. Available from: http://www.ucl.ac.uk/~uccaati/Energy.html [Accessed 19th October 2012].
↑ S.Xie, Y.Song, Z.Liu, In situ high-pressure study of ammonia borane by Raman and IR spectroscopy [ONLINE]. Available from: http://publish.uwo.ca/~ysong56/Publications/Pub40_NH3BH3_CJC.pdf [Accessed 19th October 2012].
↑ Department of Chemistry, University of Western Ontario, Aromaticity. [ONLINE]. Available from: http://instruct.uwo.ca/chemistry/373f/Nifty%20Stuff/aromaticity%201.htm [Accessed 18th October 2012].

[Tl-Br-1] J.Glaser, G.Johansson.On the Structures of the Hydrated Thallium(III) Ion and it's Bromide Complexes in Aqueous Solution. Department of Inorganic Chemistry, Royal Institute of Technology, Sweden. [Online] 1982: 125. Available from: http://actachemscand.dk/pdf/acta_vol_36a_p0125-0135.pdf [Accessed: 19th October 2012]

[molecular_orbitals_of_borane-2] Dr. Hunt, Hunt Research Group, Department of Chemistry, Imperial College London, BH3 Tutorial Problem [ONLINE]. Available from: http://www.huntresearchgroup.org.uk/teaching/teaching_comp_lab_year3/Tut_MO_diagram_BH3.pdf [Accessed 18th October 2012].

[Conversion-3] Dr. Antonio Tilocca, Royal Society Uinversity Research Fellow, University College London, Main Energy conversion factors [ONLINE]. Available from: http://www.ucl.ac.uk/~uccaati/Energy.html [Accessed 19th October 2012].

[literature-4] S.Xie, Y.Song, Z.Liu, In situ high-pressure study of ammonia borane by Raman and IR spectroscopy [ONLINE]. Available from: http://publish.uwo.ca/~ysong56/Publications/Pub40_NH3BH3_CJC.pdf [Accessed 19th October 2012].

[molecular_orbitals-5] Department of Chemistry, University of Western Ontario, Aromaticity. [ONLINE]. Available from: http://instruct.uwo.ca/chemistry/373f/Nifty%20Stuff/aromaticity%201.htm [Accessed 18th October 2012].

[1]

[2]

[3]

[4]

[5]

Optimisation

3-21G optimisation of BH3 Molecule

631G(d,p) optimisation of BH3 Molecule

LanL2DZ optimisation of TlBr3 Molecule

GEN optimisation of BBr3 Molecule

Comparing and Contrasting the bond distances of BH3, BBr3 and TlBr3

Frequency Analysis

631G(d,p) frequency Analysis of BH3 Molecule

LanL2DZ frequency Analysis of TlBr3 Molecule

Molecular Orbitals

Molecular orbitals of BH3

NBO Analysis

631G(d,p) optimisation of NH3

631G(d,p) frequency Analysis of NH3

631G(d,p) NBO analysis of NH3

Association energies: Ammonia-Borane

631G(d,p) optimisation of NH3BH3

631G(d,p) frequency analysis of NH3BH3

Mini Project

Benzene

631G(d,p) optimisation of Benzene

631G(d,p) frequency analysis of Benzene

MO analysis of Benzene

NBO analysis of Benzene

Boratabenzene

631G(d,p) optimisation of Boratabenzene

631G(d,p) frequency analysis of Boratabenzene

MO and NBO analysis of Boratabenzene

Pyridinium

631G(d,p) optimisation of Pyridinium

631G(d,p) frequency analysis of Pyridinium

MO and NBO analysis of Pyridinium

Borazine

631G(d,p) optimisation of Borazine

631G(d,p) frequency analysis of Borazine

MO and NBO analysis of Borazine

Charge distribution and MO comparison

Pi(1) totally bonding orbital

Pi(2) orbital

Pi(5) orbital

References

3-21G optimisation of BH₃ Molecule

631G(d,p) optimisation of BH₃ Molecule

LanL2DZ optimisation of TlBr₃ Molecule

GEN optimisation of BBr₃ Molecule

Comparing and Contrasting the bond distances of BH₃, BBr₃ and TlBr₃

631G(d,p) frequency Analysis of BH₃ Molecule

LanL2DZ frequency Analysis of TlBr₃ Molecule

Molecular orbitals of BH₃

631G(d,p) optimisation of NH₃

631G(d,p) frequency Analysis of NH₃

631G(d,p) NBO analysis of NH₃

631G(d,p) optimisation of NH₃BH₃

631G(d,p) frequency analysis of NH₃BH₃