In this computational chemistry lab, several molecules were analysed using the programme GaussView, including NH₃, H₂, N₂, and BH₃. This allowed us to obtain important thermodynamic information regarding these molecules, such as the energy and structure of their most stable conformers as well as the shapes and energies of their molecular orbitals.

NH₃

Molecule information

Summary

NH₃ Data

NH3

More info

Name

Ammonia

Calculation method

RB3LYP

Basis set

6-31G(d,p)

Final energy E(RB3LYP)

-56.55776873 a.u.

RMS Gradient Norm

0.00000485 a.u.

Point group

C_3V

N-H bond distance

1.01798 Å

H-N-H bond angle

105.741‎°

Confirming successful optimisation

         Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000072     0.001800     YES
 RMS     Displacement     0.000035     0.001200     YES

The optimisation file is linked here.

Vibrations

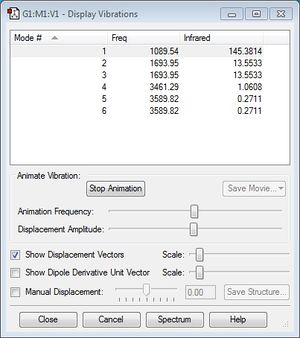
Using the 3N-6 rule, NH₃ is expected to have 3(4)-6=6 vibrational modes. This is confirmed from the results of the Gaussian output, as seen from the screenshot shown below. We can also observe that vibrational modes 2 and 3 as well as 5 and 6 are degenerate, as each pair has the same frequency and therefore the same energy. Modes 1, 2 and 3 are "bending" vibrations while modes 4, 5 and 6 are "bond stretch" vibrations. Mode 4 is highly symmetric, and mode 1 is known as the "umbrella" mode.

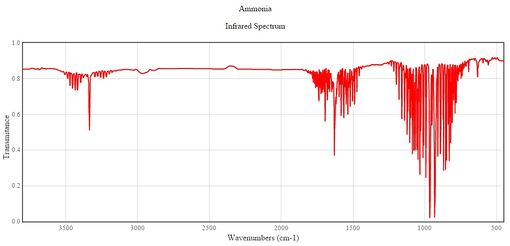
Based on this data, we can also expect to see 3 bands in an experimental infrared spectrum of gaseous ammonia. Although there are 6 vibrational modes, we would only expect to see 3 IR peaks corresponding to vibrational modes 1-4 (modes 2 and 3 give identical peaks), as the peaks of modes 5 and 6 are too weak to be observed. This is confirmed by literature IR spectrum data of ammonia, as seen below:

Atomic charge

Since N is more electronegative than H, we would expect N to have a negative charge while H to have a positive charge. This is confirmed by using GaussView, which shows that the atomic charge on N is -1.125 while that on H is 0.375.

Reactivity of NH₃: The Haber Process

The Haber-Bosch process is the main industrial process by which nitrogen gas and hydrogen gas are converted to ammonia. The process converts atmospheric nitrogen (N₂) to ammonia (NH₃) by the following reaction with H₂, using an iron catalyst at high temperatures and pressures:

N_{2} + 3 H_{2} ⟶ N H_{3}

More information can be found here.

H₂

Summary

H₂ Data

Summary

Name

Hydrogen

Calculation method

RB3LYP

Basis set

6-31G(d,p)

Final energy E(RB3LYP)

-1.17853936 a.u.

RMS Gradient Norm

0.00000017 a.u.

Point group

D_∞h

H-H bond distance

0.74279 Å

Confirming successful optimisation

         Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000001     0.001200     YES

The optimisation file is linked here.

Vibrations
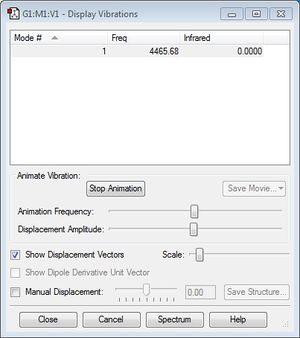
As can be seen in the screenshot below, the H₂ molecule only has 1 frequency of vibration.

Atomic charge
Since the H₂ molecule is diatomic with both atoms having the same electronegativity, the relative charge on each atom is 0 as shown below.

N₂

Summary

N₂ Data

More info

Name

Nitrogen

Calculation method

RB3LYP

Basis set

6-31G(d,p)

Final energy E(RB3LYP)

-109.52412868 a.u.

RMS Gradient Norm

0.00000060 a.u.

Point group

D_∞h

N-N bond distance

1.10550 Å

Confirming successful optimisation

         Item               Value     Threshold  Converged?
 Maximum Force            0.000001     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000000     0.001200     YES

The optimisation file is linked here.

Vibrations
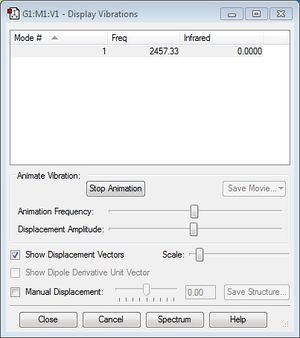
As can be seen in the screenshot below, the N₂ molecule only has 1 frequency of vibration.

Atomic charge
Since the N₂ molecule is diatomic with both atoms having the same electronegativity, the relative charge on each atom is 0 as shown below.

Energy of the Haber Process

The energy of the reaction $N_{2} + 3 H_{2} ⟶ N H_{3}$ can be computed as shown in the table below:

	Energy / a.u.	Energy / kJmol^-1
E(NH₃)	-56.55776873	-148492.42
*2E(NH₃)**	-113.11553746	-296984.84
E(N₂)	-109.52412868	-287555.60
E(H₂)	-1.17853936	-3094.255
*3E(H₂)**	-3.53561808	-9282.77
ΔE = 2E(NH₃) - [E(N₂) + 3E(H₂)]	-0.0557907	-146.48

The calculations above show that the energy for converting hydrogen and nitrogen into ammonia gas via the Haber process is -146.48 kJmol^-1, to 2 decimal places. Since the reaction is exothermic, the product NH₃ must be more stable than the reactants N₂ and H₂.

BH₃

Molecule information

Summary

BH₃ Data

BH3

More info

Name

Borane

Calculation method

RB3LYP

Basis set

6-31G(d,p)

Final energy E(RB3LYP)

-26.61532364 a.u.

RMS Gradient Norm

0.00000211 a.u.

Point group

D_3h

B-H bond distance

1.19232 Å

H-B-H bond angle

120°

Confirming successful optimisation

         Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000003     0.000300     YES
 Maximum Displacement     0.000017     0.001800     YES
 RMS     Displacement     0.000011     0.001200     YES

The optimisation file is linked here.

Vibrations

Similar to NH₃, BH₃ is expected to have 3(4)-6=6 vibrational modes using the 3N-6 rule. This is confirmed from the results of the Gaussian output, as seen from the screenshot shown below. We can also observe that vibrational modes 2 and 3 as well as 5 and 6 are degenerate, as each pair vibrates at the same frequency and therefore has the same energy. It can also be seen that modes 1, 2, 3 are "bending" vibrations while modes 4, 5 and 6 are "bond stretch" vibrations. Mode 4 in particular is highly symmetric.

Based on this data, we can also expect to see 4 bands in an experimental infrared spectrum of gaseous borane (since modes 2 and 3 as well as 5 and 6 give identical peaks).

Atomic charge

Since B is slightly less electronegative than H, we would expect B to have a slight positive charge while H to have a slight negative charge. This is confirmed by using GaussView, which shows that the atomic charge on B is 0.297 while that on H is -0.099.

Molecular orbitals

Selected molecular orbitals of BH₃ are shown and explained below.

Diagram	Energy / a.u.	Comments
	-0.51254	This bonding MO is formed from the combination of the completely in-phase bonding fragment of the H₃ unit and the 2s orbital of B. This all in-phase bonding fragment orbital is slightly lower in energy than the other fragments of the H₃ unit, which are formed partly from out-of-phase antibonding interactions and hence are slightly higher in energy. Hence, this completely in-phase bonding fragment is similar in energy to the filled 2s atomic orbital of B which is also low in energy. Thus it is able to linearly combine with it to form a bonding MO, as seen in the diagram on the left.
	-0.35079	This MO is formed from the combination of one of the fragment orbital of the H₃ unit which contains antibonding components, and the the 2p orbital of B. This results in the formation of a filled bonding MO as seen in the diagram on the left, which has the same energy as the MO in the next row.
	-0.35079	Similar to the MO above, it is formed from the combination of the other fragment orbital of the H₃ unit with antibonding components and the 2p orbital of B. This forms another filled bonding MO that is degenerate with the one above. Both these MOs are the highest occupied molecular orbitals (HOMOs) of BH₃.
	-0.06605	This is an unoccupied antibonding MO formed by the 2p_z atomic orbital of B. This orbital remains non-bonding as none of the fragment orbitals of the H₃ unit have the same symmetry and hence combination is not possible. This is the lowest unoccupied molecular orbital (LUMO) of BH₃. This indicates that BH₃ can easily accept electrons from species with higher energy HOMOs, especially since this orbital does not have a H₃ unit component and hence donation of electrons into the LUMO will not affect the overall bonding of the molecule.
	0.16839	This is also an unoccupied antibonding MO, formed by the out-of-phase interaction between the 2s atomic orbital of B and the all in-phase bonding fragment orbital of the H₃ unit. It is higher in energy than the HOMO, however it is not the highest unoccupied molecular orbital.