Rep:Mod:ss7009
SNEHA SHAH: Computational Lab Module 1
Cyclopentadiene
Dimerisation of cyclopentadiene
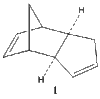
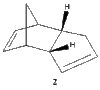
Cyclopentadiene dimerizes readily at room temperature to dicylopentadiene via a Diels Alder cycloaddition as shown in Figure 1. This system is classified as a π4s + π2s cycloaddition. Theoretically, two isomers can be formed, the exo - form and the endo - form. The exo - form arises from both bonds forming on the bottom face of the cyclopentadiene mimicking the diene (π4s) and both bonds forming on the bottom face of the cyclopentadiene mimicking the dienophile (π2s). The endo isomer involves the bonds forming to the top face of the cyclopentadiene mimicking the dienophile (π2s) [1]. However, this reaction produces the endo isomer exclusively. This unique type of stereoselectivity is observed in Diels - Alder reactions, when the diene is cyclic [2].

The Molecular Mechanics approach (MM) can be used to evaluate this specific stereoselectivity. This involves optimizing molecular geometry to an energy minimum and analyzing the individual energy contributions will give an indication of the relative stability of the isomers[3]. The results of Figure 2 (below) were obtained using the MM2 calculation from the program ChemBio3D. The most energetically stable conformer of the exo – and endo – isomer is shown. The results can be directly compared as the molecules have been drawn on the same program.
It can be seen that the energy difference between the two isomers is mainly due to torsional strain. The exo isomer has a significantly lower torsional energy than the endo isomer by 1.85 kcal /mol, indicating that it is less strained. Torsional strain occurs when atoms separated by three bonds are placed in an eclipsed conformation instead of the more stable staggered conformation [4]. Figure 3, shows the dihedral angle. Evaluation of the dihedral angle indicates that the exo isomer (179°) is specifically characteristic of the staggered conformation. This conformation illustrates the least strained, anti-periplanar relationship. However, the endo isomer (46°) does not illustrate the anti-periplanar relationship, and it is inbetween the gauche or eclipsed conformation, which is less stable and higher in energy [5].
| Exo Dimer | Endo Dimer | |
|---|---|---|
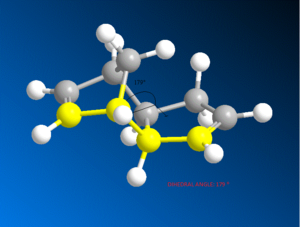 |
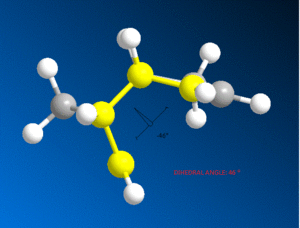 | |
Dihedral Angle 179o |
Dihedral Angle 46o |
Analysis of torsional strain supports the data that the total energy of the Exo - isomer is lower than that of the Endo – isomer by 2.12 kcal/mol. This indicates that the Exo - isomer is the more stable isomer. The more stable product is known as the thermodynamic product. However, the thermodynamic exo - product is not produced, showing that the reaction is kinetically controlled. The kinetic endo – product has lower activation energy (greater stabilization of the transition state) and it can be inferred that the endo – form will then form faster than the exo – form.
The MM approach used cannot easily model "kinetic control" of a reaction using the standard approach, since that requires knowledge of the transition state structure and energy. Frontier molecular orbital theory can be used to explain the preference of the endo- stereochemistry [2].

Figure 4 shows the favourable overlap of the p orbitals on the dienophile with the p orbitals on the diene in the endo - form. This favourable overlap helps to bring the molecules closer together and results in the formation of a stabilized transition state. These favourable interactions are absent in the exo –form [2].
Hydrogenation of cyclopentadiene
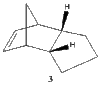
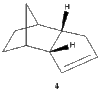
The endo product (2) formed from the kinetically controlled dimerization, can be hydrogenated to synthesize one of the dihydro derivatives (3) or (4). Further hydrogenation, would result in formation of the tetrahydro derivative (cyclopentane) [3].

As above, the Molecular Mechanics approach can be used to determine the most energetically stable conformer of each derivative and the results in Figure 6 can be directly compared.
It can be seen that the energy difference between the two dicyclopentene compounds is mainly due to bending, torsional and 1, 4 van der Waals (VDW) energy. The other energy contributions are similar in value. The dihydro derivative 4 has a significantly lower bending energy than derivative 3 by 5.34 kcal / mol. Bending energy is closely related to angular strain. Angular strain occurs when bond angles deviate from the ideal bond angles to achieve maximum bond strength in a specific chemical conformation[6]. The difference between the two derivatives is the position of the double bonds. Therefore, Figure 7 (below) illustrates the bond angles between the carbon double bond which can be compared to the ideal bond angle for the carbon sp2 hybrid state (120°). The bond angle for derivative 4 (112°) is closer to the ideal angle than for derivative 3 (108°), indicating that derivative 4 is less strained. It can be inferred that the larger bond angle of derivative 4 is due to the fact that the double bond is further away from the bridge.
| Derivative 3 | Derivative 4 | |
|---|---|---|
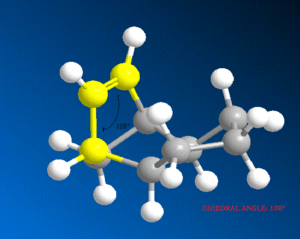 |
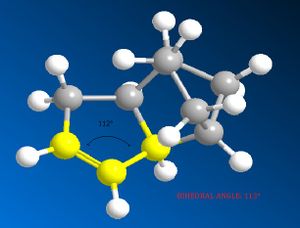 | |
Bond Angle 108o |
Bond Angle 112o |
In addition, the larger bond angle of derivative 4 indicates that both, the bonding and non – bonding electrons are as far apart as possible, which is energetically favourable [7]. This is similar to the 1, 4 van der Waals (VDW) strain argument. VDW strain occurs when two substituents in a molecule approach each other with a distance less than the sum of their VDW radii, also known as van der Waals repulsion [8]. The derivative 4 has a lower VDW energy than derivative 3 by 1.21 kcal / mol, indicating derivative 4 to have less steric hindrance, and hence, the energetically favourable compound.
Torsional strain conflicts this argument, as Figure 6 shows derivative 4 to have a higher torsional energy than derivative 3, indicating that derivative 3 should be the more stable compound. However, the other two energy terms combined (bending and van der Waals energy), quantatively, are more prominent compared to torsional energy. In addition, this theory is supported by the data as the total energy of derivative 4 is lower than that of derivative 3 by 4.54 kcal/mol. This indicates that derivative 4 is the more stable compound, the thermodynamic product.
During a reaction, the kinetic product will always be formed first rather than the thermodynamic product. If the reaction is not reversible under the conditions used, the kinetic product will be isolated [2]. Reactions such as the hydrogenation of dicyclopentadiene are usually considered irreversible. Therefore, it can be assumed that this reaction is kinetically controlled. The thermodynamic product has been determined, however, as above, in order to establish which is the kinetic product, frontier molecular orbital theory will have be used.
Intermediate in the Synthesis of Taxol
Stability of Atropisomers
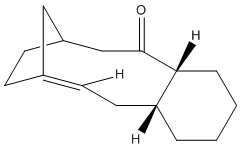
Taxol is an important drug for the treatment in ovarian cancer [3]. The organic route for synthesizing Taxol proceeds via a key intermediate. Figure 8 shows this intermediate existing as two isomers, known as atropisomers. Atropisomerism is a form of stereoisomerism that occurs in a molecule where free rotation about a single covalent bond is impeded sufficiently, resulting in different stereoisomers to be isolated [9]. This type of isomerism is especially common in the Taxol precursor due to the restricted rotation of the substituted aromatic ring within the macrocyclic structure, due to steric congestion [9]. Therefore, the intermediate can exist as isomer 9, with the carbonyl group pointing upwards and isomer 10, with this group pointing down.The stereochemistry of the carbonyl addition will be dependent on the relative stability of the isomers [3].
| Isomer 9 | Isomer 10 |
|---|---|
 |
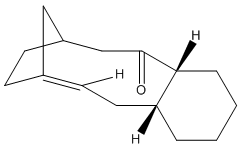 |
The MM2 force field energy technique has been utilized here to evaluate the specific stereoselectivity. This involves optimizing molecular geometry to an energy minimum. However, using ChemBio3D this required a manual edit of the structure in order to achieve the absolute minimum energy. This is because the cyclohexane ring can exist as different conformations. It is well known that the cyclohexane ring has two conformations that can be isolated in pure form; the chair and twist-boat form. The results of Figure 9 (below) were obtained using the MM2 calculation. The most energetically stable form for the different conformations of each isomer (9 and 10) is shown. Analyzing the individual energy contributions will give an indication of the relative stability of each conformation.
Comparing the different conformations of each isomer indicates the same trend for both isomers. It can be seen that the energy difference between the chair and twist-boat conformations is mainly due to bending energy. The other energy contributions are similar in value. The chair conformation has a significantly lower bending energy than the twist-boat conformation by 3.43 kcal / mol (isomer 9) and 5.94 kcal / mol (isomer 10). As above, bending energy is closely related to angular strain. The difference between the two conformations can be explained in terms of bond angle, for the chair conformation the angle is closer to the ideal bond angle of a carbon sp3 hybrid (109°) than that for the twist-boat, indicating that the chair conformation is less strained. It can be inferred that due to less angular strain, the chair conformation is lower in energy than the twist – boat for both isomers. In addition, this theory is supported by the data as the total energy of the chair conformation is lower than that of the twist-boat by 4.94 and 10.33 kcal/mol for isomer 9 and isomer 10, respectively. These values have been taken from the MM2 calculation.
Comparisons between the two isomers indicate that the energy difference is mainly due to torsional and 1, 4 van der Waals (VDW) energy. The total energy difference between the higher energy twist boat conformations of the two atropisomers is insignificant, 0.08 kcal/ mol. Analysis of the twist – boat conformation will now be disregarded, as it is assumed that the more stable chair conformation will be formed. The more stable, chair conformations of the isomers indicate a total energy difference of 5.47 kcal / mol. Isomer 10 (chair) has a significantly lower torsional energy than that of isomer 9 by 3.20 kcal /mol, indicating that it is less strained. This indicates that isomer 10 is the more stable compound, the thermodynamic product. This is the isomer with the carbonyl group pointing downwards.
A different optimization method (MMFF94) has also been used to determine the minimum energies. This method proceeds in the same way: optimizing the molecular geometry to an energy minimum and the values will give an indication of the relative stability of the isomers. This method was used, as it is useful for modeling biological systems (such as this Taxol drug intermediate) [3]. The data has been tabulated in Figure 10. The MMFF94 method provides the same conclusion as the MM2 approach does: the lowest energy (most stable) compound is the chair conformation of isomer 10. However, the MM2 and MMFF94 calculations cannot be directly compared as different parameters have been set to perform the calculations and the energy values of different force – fields cannot be correlated [3].
It has been reported that the “on standing, the compound apparently isomerizes to the alternative carbonyl isomer” [3]. From this it can be inferred that the initial intermediate formed, will be the isomer which has a lower activation barrier; therefore, this compound will be formed quicker, the kinetic product. However, on isomerization to the alternative carbonyl form, indicates that the compound is converting to the more stable form, the thermodynamic product. The data of Figure 9 shows that the most energetically stable compound is the chair conformation of isomer 10, indicating that this is the thermodynamic product. In turn, this means that the kinetic product is the chair conformation of isomer 9. The mechanism by which this interconversion of the atropisomers proceeds by is known as the oxy-Cope rearrangement [10].
Reactivity of Taxol Intermediate
It has been reported that both of the isomers react abnormally slowly, during subsequent functionalisation of the alkene [3]. This can be explained by olefinic strain, which is defined as the difference between the strain energy of an alkene and that of its corresponding alkane. Generally, bridgehead alkenes are considered to have greater strain energy than its parent alkane. This is largely due to twisting around the double bond which decreases the HOMO-LUMO difference, enhancing the reactivity [11].
However, hyperstable alkenes are often an exception to this statement due to the bridgehead location of the double bond [12]. This results due to an increase in transannular interactions between the hydrogens. Such olefins are stabilized rather than destabilized and should be thermodynamically more stable than any of their positional isomers. This results in the alkene being remarkably unreactive.
Regioselective Addition of Dichlorocarbene
Modeling of the compounds, cyclopentadiene and the Taxol intermediate revealed the strengths and limitations of the molecular mechanics approach. Moving away from this purely classical mechanical treatment to a quantum mechanical treatment of a molecule will now be used to emphasize the importance of determining the electronic aspects of a compound [3].
Orbital Control
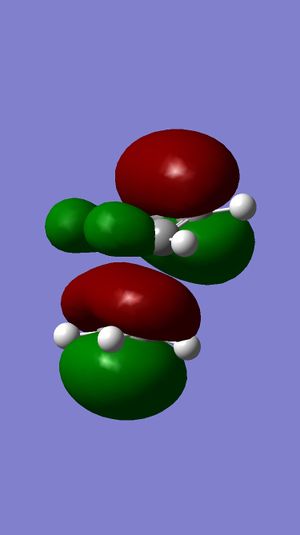
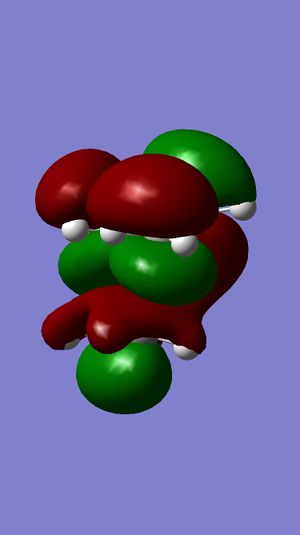
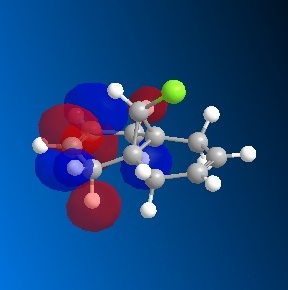
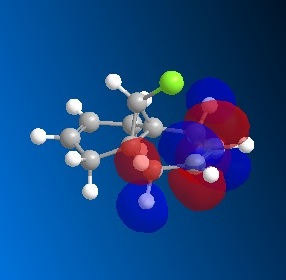
Dichlorocarbene is an electrophilic reagent, which can react with alkenes in a formal [1 +2] cycloaddition, to form genimal dichloropropanes. Compound 12 is a diene, and the electrophilic addition of dichlorocarbene is regioselective, as shown in Figure 10. This indicates the preference for attack at the endo double bond, with respect to the chlorine atom rather than the exo double bond. The molecular orbital (MO) approach has been used to model compound 12. The distribution of electron density at different molecular orbitals has been investigated as a means to rationalize the observed regioselectivity.

Initially, the MM2 method on the ChemBio3D program was used to determine the accurate geometry of the molecule. The molecule was then optimized and the energy of the orbitals was calculated using the MOPAC/RM1 MO method. A graphical display of the frontier molecular orbitals is shown below. Figure 11 shows that the molecular orbitals calculated are approximately symmetrical. This is consist with the fact that compound 12 belongs to the Cs symmetry point and will therefore display a plane of symmetry. From this it can inferred that the evaluation of the observed molecular orbitals is reliable [3].
| HOMO -1 | HOMO | LUMO | LUMO +1 | LUMO +2 | |
|---|---|---|---|---|---|
 |
 |
 |
 |
 |
The Highest Occupied Molecular Orbital (HOMO) would hold the highest energy electrons. Therefore, it is presumed that the HOMO of a molecule would dictate the nucleophilic nature of the molecule[3]. . Figure 11 shows the π-electron density in the HOMO is located on the double bond endo to the chlorine substituent, with no electron density located on the exo double bond at all. Therefore, reaction with dichlorocarbene would render the endo double bond more susceptible to electrophilic attack.
The Lowest Unoccupied Molecular Orbital (LUMO) would hold no electrons and therefore, is presumed to be the least reactive towards electrophilic attack (nucleophilic)[3]. . Figure 11 shows the π-electron density in the LUMO is located on the antibonding C=C double bond exo to the chlorine substituent. Observations of electron density distribution in the molecular orbitals of the HOMO and LUMO support the selective addition of dichlorocarbene.
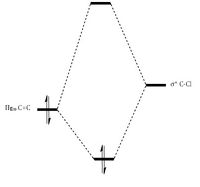
The regio-selection is a consequence of antiperiplanar interactions between the occupied exo π-orbital and the empty σ* C-Cl orbital. This interaction produces a large splitting for the exo double bond. The C-Cl bond is driven down in energy due to the electronegative chlorine, resulting in the two orbitals being closer in energy as seen in Figure 12. In addition, the orbitals are in the right orientation to interact well. These two factors lead to a large orbital overlap, leading to a large splitting energy and in turn, large stabilization energy. A similar antiperiplanar interaction cannot be produced for the endo double bond, as the orbitals are not in the right orientation. Hence this stabilization energy is seen only for the exo double bond only. The extra stability renders the bond less reactive towards an electrophile [13]. MO Theory explains the electron distribution shown in the frontier molecular orbitals and the regioselective addition of dichlorocarbene.
Vibrational Frequencies
Compound 12 and its hydrogenated derivative, where a single C-C bond replaces the exo double bond (Figure 12), are optimized as above and then subjected to B3LYP6-31G (d,p) [3]. This produced infrared spectra (Figure 13) and the corresponding vibrational frequencies have been tabulated. This method will allow comparisons between the two compounds to be made, which will provide supporting data for the above analysis.
| Infrared Stretching Frequencies | |||
| Compound | 12 | 13 | |
|---|---|---|---|
| Image |  |  | |
| 3D Image | |||
| C-Cl/ cm-1 | 748.10 | 756.80 | |
| C=C endo/ cm-1 | 1752.21 | 1749.38 | |
| C=C exo/ cm-1 | 1727.03 | - | |
| Compound 12 | Compound 13 | |
|---|---|---|
 |
 |
Compound 12 has a lower C-Cl stretching frequency (748.10 cm-1) than compound 13(756.80cm-1). This is attributed by the orbital interactions affecting the bond in compound 12. As analyzed above, the π C=C exo double bond is in the right orientation to interact with the σ* C-Cl bond in compound 12. This interaction results in a gain in electron density for the C-Cl orbital. As this is an antibonding orbital, it is disfavoured and will weaken the bond, represented by a lower frequency. There is no C=C exo double bond in compound 13, therefore it does not possess any such interactions and the stretching frequency of the C-Cl is a true reflection of its energy without any orbital influences.
The C=C endo stretching frequency correlates well for compound 12 and 13 with values of (1752.21cm-1) and (1749.38cm-1) respectively. However, for compound 12, the two carbon double bonds have different bond strengths. The endo bond has a stretching frequency, which is 25.18cm-1 higher than the exo frequency. This is because the orbital overlap to the σ* C-Cl orbital, results in the electron density becoming more delocalized and diffuse. Once again, the exo carbon double bond is weakened and results in a lower stretching frequency. The endo carbon double bond does not have this delocalization. The electron density is more concentrated and strengthens the endo bond. In turn, the localization of the electron density drives the nucleophilic nature of the endo carbon double bond. To summarize, this full investigation of regioselectivity and reactivity is rationalized by the orbital interactions of the π C=C exo orbital to the σ* C-Cl orbital.
Monosaccaride Chemistry: Glycosidation
Sugars can undergo a glycosidation reaction which involves forming a new glycosidic bond at the anomeric centre. The leaving group (e.g. X= Br) at the anomeric centre can be attacked by a nucleophile. The reaction proceeds via the planar oxonium ion (A and B in Figure 15). Two anomers (α and β) can be formed depending on orientation of the OAc group on the adjacent carbon. This diasterospecifity is a consequence of the neighbouring group affect.
The neighbouring group affect is shown in Figure 15. The carbonyl of the 2-acetyl can stabilize the oxonium ion, blocking one face. In turn, this forces the nucleophile to attack on the opposite face as shown by the intermediates C and D. Therefore, the product has 1, 2 trans stereospecificity with respect to the –OAc group and the desired glycosidic substituent. The β-anomer is formed when the neighouring group effect initiates from the botton face, which will lead to the nucleophile attacking from the top face. In comparison, the α-anomer is formed when the nucleophile is forced to attack from the bottom face [3].
The –OR substituents on the sugar represent protecting groups. Usually, in sugar chemistry, these substituents are –OAc groups. For this modelling method, using acetyl groups would keep the chemistry accurate, however, acetyl group are sterically demanding, and 4 acetyl groups around a molecule would complex the conformational analysis. In addition, the acetyl groups possess oxygens and hydrogens, leading to strong hydrogens bonds. These interactions would influence the optimized geometry and would therefore not lead to accurate results.
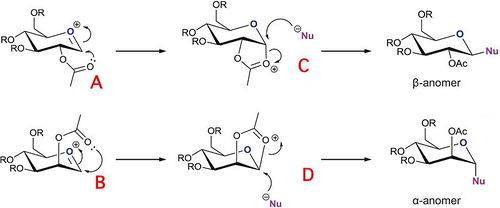
A more reasonable protecting group to use is –OME (R=CH3). Methyl groups do not form any such interactions, rendering the optimization calculations formed reliable. In addition, the methyl group is smaller and hence not as sterically demanding; 4 methyl groups bonded to a molecule rather than 4 acetyl groups would keep the conformational demand as minimal as possible, whilst still representing the chemistry of the oxonium ions and intermediates in the glycosidation reaction.
Figure 16 shows the structures of the two cations shown in Figure 15 (A and B) and the corresponding intermediates (C and D respectively). The MM2 and MOPAC/PM6 MO optimization method has been used here to model the structures and their relative energies have been recorded. For a comparison, the other conformer of each structure has also been analysed (A’, B’, C’ and D’). Both methods can optimize molecular geometry to an energy minimum. However, as discussed above, the molecular mechanics approach fails to consider molecular orbital theory. Neighbouring group participation is based on orbital interactions initiated by the carbonyl oxygen orbital interacting with the anomeric centre. Therefore consideration of molecular orbital theory is vital for the glycosidation reaction as the neighbouring group effect corresponds to the observed diastereospecificity. It can be inferred that the MOPAC/PM6 MO approach is better suited to this task and will produce more reliable results.
| Oxonium Cations & Intermediates of Gylcosidation Reaction | |||||
| Oxonium cation | Total Energy (MM2)/ kcal/ mol | Image (MM2) | Total Energy (PM6)/ kcal/ mol | Image (PM6) | |
| A | 19.88 | -91.64 | |||
| A' | 33.09 | -77.40 | |||
| B | 22.13 | -85.95 | |||
| B' | 34.52 | -77.52 | |||
| C | 32.45 | -91.65 | |||
| C' | 43.36 | -67.88 | |||
| D | 40.93 | -84.07 | |||
| D' | 45.78 | -66.73 | |||
In general, Figure 16 shows that the conformers A, B, C and D are all lower in energy than A’, B’, C’ and D’. Conformer A has the –OAc group equatorial and the acetyl group pointing below the plane of the oxonium cation and A’ has the –OAc group equatorial and the acetyl group pointing above the plane. It can be seen from MM2 analysis that the energy difference between the two conformers is mainly due to charge-dipole interactions (Figure 17). Conformer A has a significantly lower charge-dipole energy than the A’. This suggests that the geometry of conformer A is such that the carbonyl oxygen of the acetyl is placed in a position where it can make favourable interactions and attack the oxonium cation well. In addition, there are less repulsive and unfavourable interactions in A than A’. Conformer B has the –OAc group axial and the neighbouring acetyl group pointing above the plane of the oxonium cation and B’ has the –OAc group axial and the group pointing above the plane. Similar to A, B is lower in energy than B’ due to more favourable charge-dipole interactions. The MM2 and MOPAC/PM6 method both produce the same conclusion.
For the intermediates C and D, two conformers of each can also be produced. Intermediate C has the 5 – membered ring equatorial, pointing below the plane of the molecule and its conformer C’ has the ring pointing above the plane. It can be seen from MM2 analysis that the energy difference is a combination of factors but it comes down to mainly strain (Figure 17). This is logical as the geometry of C’ is when the ring has one bond axial and the other equatorial. Therefore, it is essentially ‘trans’, which would lead to angular strain and is very unfavourable. Intermediate C is lower in energy than C’. Conformer D has the oxonium ring axial, pointing above the plane and D’ has the ring pointing below. Similar to C, D is lower in energy than D’ due to less strain. The MM2 and MOPAC/PM6 method both produce the same conclusion.
| Cations & Intermediates of Glycosidation Reaction | |||||||||
| Type of Energy Contribution | Energy of A/ kcal/ mol | Energy of A'/ kcal/ mol | Energy of B/ kcal/ mol | Energy of B'/ kcal/ mol | Energy of C/ kcal/ mol | Energy of C'/ kcal/ mol | Energy of D/ kcal/ mol | Energy of D'/ kcal/ mol | |
| Stretch | 2.57 | 2.55 | 2.48 | 2.58 | 2.06 | 2.41 | 1.91 | 2.99 | |
| Bend | 11.04 | 8.60 | 10.69 | 11.12 | 13.83 | 18.15 | 14.67 | 18.09 | |
| Stretch-Bend | 1.01 | 0.92 | 0.98 | 0.94 | 0.75 | 0.65 | 0.62 | 0.89 | |
| Torsion | 1.93 | 3.57 | 3.22 | 1.29 | 9.54 | 6.01 | 8.11 | 9.32 | |
| Non-1, 4 VDW | 1.10 | -2.57 | -1.94 | -0.94 | -2.77 | -4.58 | -4.55 | -2.98 | |
| 1, 4 VDW | 18.64 | 19.52 | 19.15 | 18.76 | 17.71 | 19.35 | 18.27 | 19.26 | |
| Charge-Dipole | -22.91 | -1.50 | -9.26 | -12.30 | -7.72 | 1.02 | 3.14 | -0.70 | |
| Dipole-Dipole | 6.52 | 3.20 | 5.88 | 4.75 | -2.16 | -1.13 | 0.03 | -1.00 | |
An additional observation is that the MOPAC/PM6 method shows the energy of A to be equal to the energy of C and the energy of B to equal the energy of D. This suggests the oxonium cation is modelled as the same structure as its corresponding intermediate. This is correct and should be what is observed as MOPAC/PM6 takes the neighbouring group effect into consideration. This highlights the differences between MM2 and MOPAC/PM6 approach.
Computational analysis can explain the diastereospecifity. A and B are more reactive than A’ and B’; which leads to C and D, that are more stable than C’ and D’. Once C and D are formed, the nucleophile is forced to attack from the opposite face as the ring is blocking one whole side. This forms the diastereoisomers: α-anomer and the β-anomer.
Investigating the regioselectivity of the Baeyer Villiger Reaction
Many reactions carried out by synthetic chemists produce a mixture of products [3]. The Baeyer Villiger Reaction has been used in the recent synthesis of analogues of beta lactam antibiotics. Beta lactam antibiotics are becoming growingly important in the fight against bacteria. It has been reported that they show excellent activity against Gram—positive and Gram-negative bacteria. In addition, they are resistant to attack by the corresponding enzymes [16]. Therefore, this product is becoming extensively researched and its synthetic route is being analysed as well.
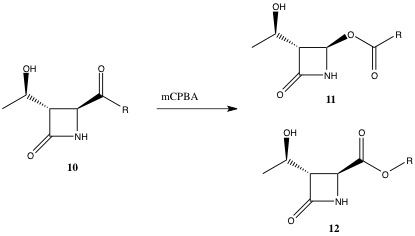
The Baeyer Villiger Reaction is an organic process involving the oxidation of a ketone to an ester. This reaction proceeds via treatment with mCPBA under acidic conditions. As shown in Figure 18, this procedure has effectively inserted an oxygen atom in between the carbonyl group and the alpha carbon. The characteristic feature of this reaction is that it is regioselective, forming two possible isomers [3]. One isomer (Compound 11) involves the oxygen to be inserted next to the azetidinyl moiety and the other isomer (Compound 12) involves the oxygen to be inserted next to the side group, R.
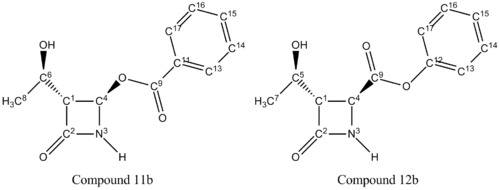
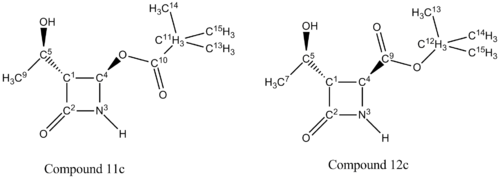
Varying the R group with different substituents, will result in different ratios of the isomeric mixture. This investigation follows compound 11 and 12 when R = -CH(CH3)2 (isopropyl), -C6H6 (phenyl) and –C(CH3)3 (tertiary butyl).The MM2 and MOPAC/PM6 MO optimization method has been used here to model the structures and their relative energies have been recorded. A 3D image of each compound has also been included for visual purposes. The two regioisomers have been differentiated using 13C NMR and 15N NMR spectroscopy; the spectra have been calculated by the GIAO approach using the quantum mechanical density functional theory. The carbons for the carbonyls of esters and amides only, have been corrected using δcorr = 0.96δcalc + 12.2 due to systematic errors. These values have then been compared to literature values where possible. From this analysis, it is possible to predict which isomer will predominate.
A vital intermediate in the Baeyer Villiger Reaction is the Criegee intermediate. This intermediate can follow two different migrating routes resulting in two different isomers, as shown below. Varying the R group with different substituents, will result in different ratios of the isomeric mixture. From this analysis, it is possible to predict which isomer will predominate.

R Substituent: -CH(CH3)2 (isopropyl)
| R Substituent = -CH(CH3)2(isopropyl) | |||
| Type of Energy Contribution | Energy of Compound 11a/ kcal/ mol | Energy of Compound 12a/ kcal/ mol | |
| Stretch | 2.44 | 2.41 | |
| Bend | 36.18 | 44.00 | |
| Stretch-Bend | -0.53 | -0.20 | |
| Torsion | 9.97 | 7.98 | |
| Non-1, 4 VDW | -6.20 | -2.50 | |
| 1, 4 VDW | 5.67 | 5.84 | |
| Dipole-Dipole | -4.46 | 0.25 | |
| Total Energy (MM2) | 43.07 | 57.79 | |
| Image (MM2) |
|
||
| Total Energy (MOPAC/PM6) | -182.14 | -170.61 | |
| Image (PM6) |
|
||
| Compound 11a | Compound 12a | |
|---|---|---|
 |
 |
| Compound 11a | Compound 12a | |
|---|---|---|
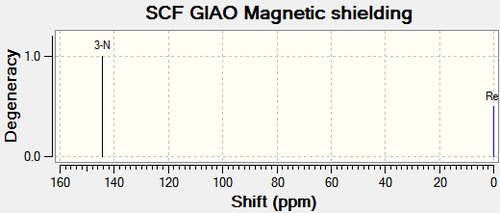 |
 |
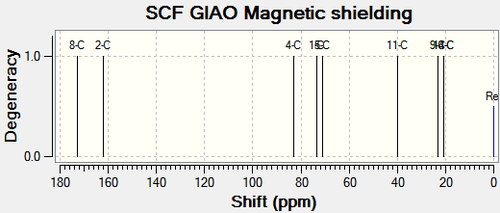
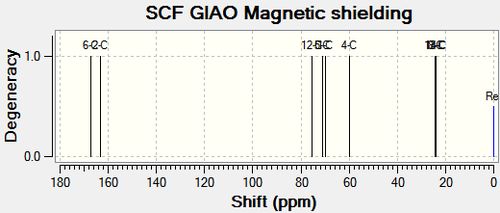
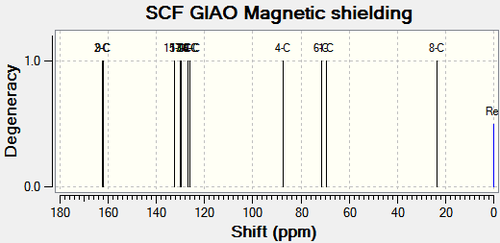
Chemical Shift Values for 13C and 15N NMR Spectra for Compound 11a and Compound 12a | |||||||
| Carbon/Nitrogen Number for compound 11a | Chemical Shift(δ) for compound 11a (calculated)/ppm | Chemical Shift(δ) for compound 11a (corrected)/ppm | Chemical Shift(δ) for compound 11a (literature)[21]/ppm | Carbon/Nitrogen Number for compound 12a | Chemical Shift(δ) for compound 12a (calculated)/ppm | Chemical Shift(δ) for compound 12a (corrected)/ppm | Chemical Shift(δ) for compound 12a (literature)[21]/ppm |
|---|---|---|---|---|---|---|---|
| 8-C (ester carbonyl) | 172.68 | 177.97 | 177.6 | 6-C (ester carbonyl) | 167.19 | 172.70 | 170.8 |
| 2-C (amide carbonyl) | 162.19 | 167.90 | 167.2 | 2-C (amide carbonyl) | 163.41 | 169.07 | 168.3 |
| 4-C | 83.04 | 83.04 | 75.9 | 4-C | 59.98 | 59.98 | 50.0 |
| 1-C | 73.34 | 73.34 | 65.2 | 1-C | 69.88 | 69.88 | 64.0 |
| 5-C | 70.94 | 70.94 | 63.9 | 5-C | 71.19 | 71.19 | 64.5 |
| 11-C | 40.02 | 40.02 | 34.0 | 12-C | 75.56 | 75.56 | 69.7 |
| 9-C | 23.11 | 23.11 | 21.3 | 8-C | 24.01 | 24.01 | 21.3 |
| 13-C | 20.74 | 20.74 | 18.9 | 13-C | 24.53 | 24.53 | 21.9 |
| 14-C | 20.68 | 20.68 | 18.8 | 14-C | 24.12 | 24.12 | 21.8 |
| 3-N | 144.30 | 144.30 | - | 3-N | 132.20 | 132.20 | - |
The calculated NMR chemical shifts for compound 11a and 12a are close to the literature values for the 13C spectrum. there was no literature values available for the 15N spectrum. Analysis of the tabulated NMR data will help to distinguish between the two compounds. The main differences are between C11 & C12 for compound 11a and 12a respectively and between C4 for both compounds. This is expected as the purpose of this analysis is to determine which carbon the oxygen is next to and which carbon the carbonyl group is next to.
C11 and the corresponding carbon on compound 12a (C12) is the central carbon on the isopropyl substituent (Figure 23). The chemical shift for the carbon on compound 11a is 35.54ppm lower than that on compound 12a.This indicates that the C11 atom has a more upfield shift than C12, as a result of C11 being more shielded due to greater electron density. The carbonyl group (EDG) would enforce more shielding than the oxygen atom (EWG). The chemical shift for C4 on compound 11a is 23.06ppm higher than that on compound 12a. It can be inferred that the carbon on compound 11a is less shielded than the corresponding carbon on compound 12a. As above, the oxygen atom would not produce as high a chemical shift as carbonyl would. Analysis of the two carbons on each compound reveals the correct structures.
The 15N NMR spectrum supports the above analysis. The nitrogen for Compound 11a has a higher chemical shift than the nitrogen in compound 12a. This is a result of the nearby electron withdrawing ability in compound 11a as opposed to compound 12a.
R Substituent: -C6H6 (phenyl)
| R Substituent = -C6H6 (phenyl) | |||
| Type of Energy Contribution | Energy of Compound 11b/ kcal/ mol | Energy of Compound 12b/ kcal/ mol | |
| Stretch | 3.61 | 2.36 | |
| Bend | 42.18 | 35.74 | |
| Stretch-Bend | -0.68 | -0.69 | |
| Torsion | 8.45 | 7.57 | |
| Non-1, 4 VDW | -1.02 | -6.68 | |
| 1, 4 VDW | 10.65 | 9.83 | |
| Dipole-Dipole | 1.68 | 0.01 | |
| Total Energy (MM2) | 64.87 | 48.15 | |
| Image (MM2) |
|
||
| Total Energy (MOPAC/PM6) | -131.74 | -125.35 | |
| Image (PM6) |
|
||
| Compound 11b | Compound 12b | |
|---|---|---|
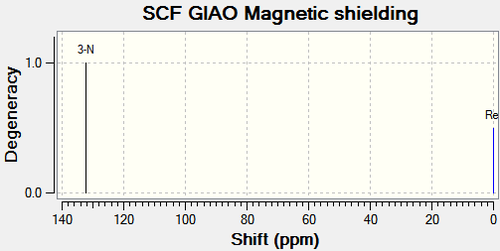
 |
 |
| Compound 11b | Compound 12b | |
|---|---|---|
 |
 |
There are no literature NMR data available for compound 11b and 12b. The chemical shift for C4 on compound 11b is 25.9ppm higher than that on compound 12b as shown in Figure 27. From the same reasons as above, this is due to the electron withdrawing nature of the oxygen atom next to C4 on compound 11b, deshielding the carbon. This corresponds with the 15N NMR spectrum; the oxygen atom also lowers the chemical shift of the nitrogen compared to compound 12a. The other major difference is C11 and C12 on compound 11b and 12b respectively. C11 is 25.03ppm lower than C12 due to the carbonyl donating electron density, shielding the carbon. This analysis coincides exactly with the analysis of compound 11a and 11b above.
R Substituent: -CH2CH2CH3 (tertiary butyl)
| R Substituent = -CH2CH2CH3 (tertiary butyl) | |||
| Type of Energy Contribution | Energy of Compound 11c/ kcal/ mol | Energy of Compound 12c/ kcal/ mol | |
| Stretch | 2.70 | 2.52 | |
| Bend | 36.48 | 38.09 | |
| Stretch-Bend | -0.43 | -0.38 | |
| Torsion | 10.70 | 7.89 | |
| Non-1, 4 VDW | -6.42 | -4.95 | |
| 1, 4 VDW | 6.48 | 6.69 | |
| Dipole-Dipole | -4.51 | -2.34 | |
| Total Energy (MM2) | 45.00 | 47.51 | |
| Image (MM2) |
|
||
| Total Energy (MOPAC/PM6) | -187.91 | -190.73 | |
| Image (PM6) |
|
||
| Compound 11c | Compound 12c | |
|---|---|---|
 |
 |
| Compound 11c | Compound 12c | |
|---|---|---|
 |
 |
There are no literature NMR data available for compound 11c and 12c. C11 and the corresponding carbon on compound 12c (C12), is the central carbon in the tertiary butyl substituent. The trends in chemical shift differences are consistent with compound 11a, 11b, 12a and 12b. The oxygen atom next to C4 in compound 11c deshields the carbon resulting in a higher chemical shift value compared to compound 12c. C11 has a lower chemical shift value than C12 as it is more shielded.15N NMR analysis shows that the nitrogen in compound 11c has a higher chemical shift value by 16.79ppm (figure 31), which is consistent with the above analysis.
All three substituents lead to the same conclusion; the main carbons affected are the carbons next to the oxygen and the carbon next to the carbonyl. Comparisons between the spectroscopic data of compound 11 and 12 allow the two molecules to be differentiated.
Regiochemical Outcome
The different substituents do not affect the trend of the chemical shifts tabulated from the spectroscopic data. However, they do affect the regioselectivity. As explained above, the regioselectivity is dependent on which migration route the Criegee intermediate is likely follow. Formation of compound 12 involves the intermediate to form a carbocation initially. The oxygen lone pair from the hydroxyl group then forms the carbonyl double bond. Therefore, formation of compound 12 is dependent on the relative stability of the carbocation. Tertiary butyl is able to stabilize the positive charge and the migrating ability of this group is known to be good [16]. Therefore, if the substituent is the tertiary butyl group, there is exclusive formation of compound 12c.
The phenyl substituent is not able to stabilize the positive charge well at all. Therefore, with this substituent, the regioselectivity is inverted. In addition, as the phenyl substituent is bulky comparatively, the Criegee intermediate would not prefer to migrate this group. The migration pathway to produce compound 11 is favoured with increasing s character. As the phenyl group has significantly more s character than the alkyl groups, this renders compounds 11b the exclusive product.
The isopropyl substituent produces an equimolar mixture of 11a: 12a. Compound 12 is produced because the alkyl group is able to stabilize the positive charge. However, its ability to stabilize the charge is less than that of the tertiary butyl group. This is due to the fact that there are a reduced number of C-H bonds involved in the hyperconjugative stabilization of the positive charge (6 bonds in the isopropyl compared to 9 bonds for tertiary butyl) [16]. In addition, the isopropyl group does not have as great a migrating ability as tertiary butyl, due to its intermediate strengths, it does not exclusively produce compound 12 and will therefore, produce an equimolar mixture.
References
<references>
- ↑ http://www.ch.ic.ac.uk/local/organic/pericyclic/
- ↑ 2.0 2.1 2.2 2.3 2.4 http://www.enc.edu/~timothy.t.wooster/courses/CH322/Lab/3-21%20The%20Diels%20Alder%20reaction.pdf
- ↑ 3.00 3.01 3.02 3.03 3.04 3.05 3.06 3.07 3.08 3.09 3.10 3.11 3.12 3.13 3.14 3.15 Third year Chemistry Computation Lab Module 1:Organic
- ↑ Anslyn and Dougherty, Modern Physical Organic Chemistry, University Science Books, 2006, ISBN 978-1891389313
- ↑ http://www.ch.ic.ac.uk/local/organic/conf/
- ↑ Wade, L. G. "Structure and Stereochemistry of Alkanes." Organic Chemistry. 6th ed. Upper Saddle River, NJ: Pearson Prentice Hall, 2006. 103-122. Print.
- ↑ Wiberg, K. (1986). "The Concept of Strain in Organic Chemistry". Angew. Chem. Int. Ed. Engl. 25: 312–322. doi:10.1002/anie.198603121.
- ↑ Organic chemistry 4th. Ed., Morrison and Boyd ISBN 0-205-05838-8
- ↑ 9.0 9.1 Lloyd-Williams, P.; Giralt, E. Chem. Soc. Rev., 2001, 30, 145
- ↑ S. W. Elmore and L. Paquette, Tetrahedron Letters, 1991, 319; DOI:10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0
- ↑ http://pubs.acs.org/doi/pdf/10.1021/ja00398a003
- ↑ http://pubs.acs.org/doi/pdf/10.1021/ja00398a003
- ↑ http://pubs.rsc.org/en/content/articlepdf/1992/p2/p29920000447
- ↑ Infrared Spectrum Publication of Compound 12: http://hdl.handle.net/10042/to-10359
- ↑ Infrared Spectrum Publication of Compound 13:http://hdl.handle.net/10042/to-10365
- ↑ 16.0 16.1 16.2 http://pubs.acs.org/doi/pdf/10.1021/jo030377y
- ↑ 13C NMR Spectrum Publication of Compound 11a: http://hdl.handle.net/10042/to-10378
- ↑ 13C NMR Spectrum Publication of Compound 12a:http://hdl.handle.net/10042/to-10379
- ↑ 15N NMR Spectrum Publication of Compound 11a: http://hdl.handle.net/10042/to-10378
- ↑ 15N NMR Spectrum Publication of Compound 12a:http://hdl.handle.net/10042/to-10379
- ↑ 21.0 21.1 http://pubs.acs.org/doi/suppl/10.1021/jo030377y/suppl_file/jo030377y_s.pdf
- ↑ 13C NMR Spectrum Publication of Compound 11b: http://hdl.handle.net/10042/to-10382
- ↑ 13C NMR Spectrum Publication of Compound 12b: http://hdl.handle.net/10042/to-10383
- ↑ 15N NMR Spectrum Publication of Compound 11b:http://hdl.handle.net/10042/to-10382
- ↑ 15N NMR Spectrum Publication of Compound 12b:http://hdl.handle.net/10042/to-10383
- ↑ 13C NMR Spectrum Publication of Compound 11c:http://hdl.handle.net/10042/to-10384
- ↑ 13C NMR Spectrum Publication of Compound 12c: http://hdl.handle.net/10042/to-10385
- ↑ 15N NMR Spectrum Publication of Compound 11c:http://hdl.handle.net/10042/to-10384
- ↑ 15N NMR Spectrum Publication of Compound 12c:http://hdl.handle.net/10042/to-10385