Rep:Mod:ss11012complab

EX₃

Geometry info - bond angles and distances

Geometry Data

	BH3	BBr3	GaBr3
r(E-X)	1.19231	1.93396	2.35017
θ(X-E-X)	120.006	120.000	120.000

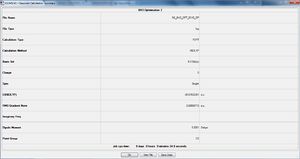
BH₃ Optimisation

B3LYP/3-21G level

Optimisation log file here

Summary data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000220 0.000450 YES RMS Force 0.000106 0.000300 YES Maximum Displacement 0.000919 0.001800 YES RMS Displacement 0.000447 0.001200 YES	optimised borane molecule

Explicitly determined point group of BH₃ is D_3h.

B3LYP/6-31G(d,p) level - A better basis set

Optimisation log file here

Summary data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000012 0.000450 YES RMS Force 0.000008 0.000300 YES Maximum Displacement 0.000063 0.001800 YES RMS Displacement 0.000039 0.001200 YES	optimised borane molecule

Explicitly determined point group of BH₃ is D_3h.

GaBr₃ Optimisation

B3LYP/LANL2DZ level

Optimization log file DOI:10042/101496

Summary Data	Convergence	Jmol
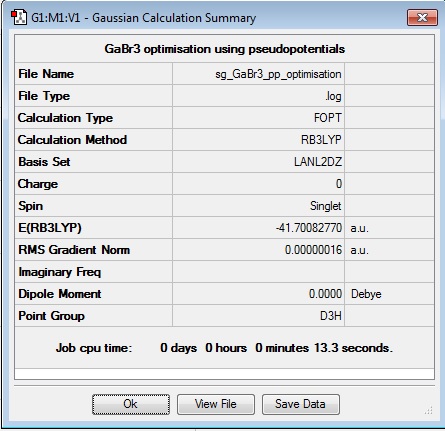	Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000003 0.001800 YES RMS Displacement 0.000002 0.001200 YES	Optimised GaBr

BBr₃ Optimisation

B3LYP/6-31G(d,p)LANL2DZ level

Optimization log file DOI:10042/101605

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000008 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.000036 0.001800 YES RMS Displacement 0.000024 0.001200 YES	Optimised BBr

Structure comparison - Day 2 Section's Questions

What are the similarities and differences in the three molecules you have optimised?

EX3 – Using purely a sized based argument, we can explain the trend seen in the EX3 computed bond lengths. A common assumption is that only valence electrons are involved in bonding. Heavier atoms, have a “larger core electron cloud” with a corresponding greater volume, and since bond lengths are defined as the distances between the two nuclei, is it clear that a heavier atoms involvement invokes a larger bond distance.

Bond lengths of 119.2, 193.3 and 235 pm were computed for BH3, BBr3 and GaBr3 respectively. It is evident that when moving from BH3 to BBr3 to GaBr3 an increasing E-X bond length is expected, this is confirmed by the computations. In the most simple and very approximate case one can sum the covalent radii of the counterparty atoms involved in the E-X bond, giving a very rudimentary picture of expected bond lengths. Covalent radii are simply a function of the electron count of an atom, the larger this is, the larger the electron cloud of the atom, of which the valence wavefunctions interact to form bonds. This method, based on atom size, predicts bond lengths of BH3, BBr3 and GaBr3 115, 204 and 238 pm respectively. By simply summing covalent radii one is, however, under the assumption that solely 100% covalent bonding prevails, however this may not reflect the true bonding picture, and for this MO theory is required. Any discrepancies between the above and the computed bond lengths can be explained by either error in our computations and something a little more interesting. Firstly we must establish the difference between the group 3 elements, B and Ga. Both are electron deficient in EX3 compounds and both have the ability to accept electron density into vacant orbitals, commonly referred to as Lewis acids. The difference between the two is that, B is a more effective Lewis acid than Ga, simply because its valence orbitals are less diffuse and lower energy atomic wavefunctions.

Now we can easily explain the effect of changing the ligand from H to Br. Br with its occupied and non-bonding p orbitals can donate electron density into the perpendicular vacant p orbital of B or Ga (picture sp2 hybridisation) forming some additional bonding character above and below the trigonal planar molecule. Hydrogen atoms, on the other hand, clearly cannot. This explains why the computed bond lengths for BBr3 and GaBr3 are smaller the predicted by covalent radii additions. When we move from BBr3 to GaBr3 however the discrepancy between the computed and predicted decreases. This is perhaps because, Ga, being a less effective Lewis acid, exhibits a less pronounced conjugative effect. BH3 computed distance comes very close to the predicted, this effect however is not present, the discrepancy could be attributed to both computational/literature error. Since the molecules are highly symmetric, there are no effects which cause deviations from the 120 degrees bond angle in all three EX3 optimised molecules.

What is a bond?

A bond is an energetically favourable orientation of nuclei and their respective electron density within space. Although radiation and nuclear motion, can causes deviations from this arrangement, the energy minimum on the PES v distance graph reflects the most thermodynamically stable arrangement, i.e. the “bond”. Since, this arrangement is the lowest in energy, it will remain, subject to no forces acting upon the matter involved. More creatively, a bond can be thought of two positively charged nuclei with the electron density in the region between them, since we know bonds are sustainable (otherwise we couldn’t form molecules), put very simply, there is a net attractive interaction within the system (the electron – nuclei interactions > electron – electron repulsions + nuclei repulsions) – this explains the stickiness of two nuclei in a bond. A more quantitative explanation of bonding within a molecule can be built up by solving the Schrodinger equation to compute molecular wavefunctions – this is what we have been doing in our optimisation/energy calculations throughout this experiment. Each electron has an associated wave-function which describes it, AO’s are interpretations of these wavefunctions, and qualitative MO’s can be formed by using these as basis sets. Other forms of bonding also include Ionic and metallic, but for the purposes of our experiment “covalent” bonding becomes a focus.

How much energy is there in a strong, medium and weak bond? Give examples of each type of bond (strong, medium and weak)

Strong bond – N2 triple bond is one of the strongest bonds known to man, with a staggering bond dissociation energy of – 945 Kj/mol Medium bond – Typical C-C bonds are relatively “medium” bonds – 350 Kj/mol Weak bond – Halogen diatomic bonds such as within I2 are relatively weak - 151 Kj/mol The above are just a few examples of bond energies, an entire different wiki would be required to barely begin tackling the vast spectrum of bonding – above is only showing “2c-2e” bonding, we can also have other forms where bridging occurs – for example “3c-2e”

Why doesn’t Gaussian always draw bonds – Pre-defined values for bond lengths are registered within the program, and bonds are only shown, subject to the distances being within there parameters. Very low level calculations may fail to represent bonds accurately.

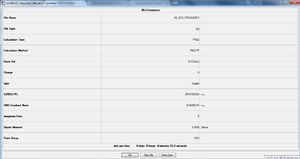
BH₃ Frequency calculation

B3LYP/6-31G(d,p) level

Frequency file: here

Summary data	Low modes
	Low frequencies --- -11.7227 -11.7148 -6.6070 -0.0005 0.0278 0.4278 Low frequencies --- 1162.9743 1213.1388 1213.1390

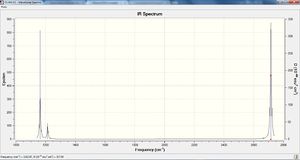
Vibrational spectrum of BH₃

wavenumber	Intensity	IR active?	type
1163	93	Yes	Bend
1213	14	Yes (slightly)	Bend
1213	14	Yes (slightly)	Bend
2583	0	No	Stretch (sym)
2715	126	Yes	Stretch (asym)
2715	126	Yes	Stretch (asym)

|

Question

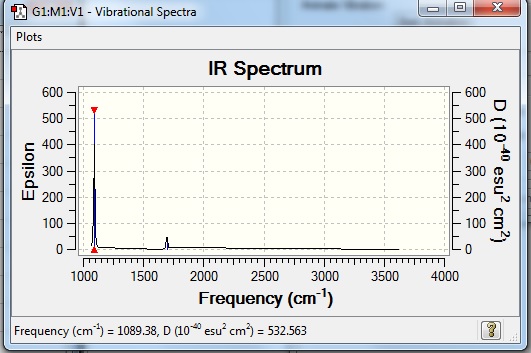
Why are there less than 6 peaks in the spectrum?

BH3 contains 4 atoms and by applying 3N-6 we can derive the total number of vibrational modes – 6. From the IR spectrum it is apparent that we don’t see 6 peaks but instead we see 3 peaks. Firstly, for a vibrational mode to be IR active we require a change in the dipole moment of the molecule upon the vibration – i.e. the vibration must asymmetric – by viewing the animations of gauss-view it is clear the vibrational mode at 2583cm-1 is a symmetric stretch and therefore not IR active, this is also confirmed as its intensity is zero. There are 5 possible IR active modes remaining, and indeed this is the case. A single IR active peak is present at 1163cm-1 but of low intensity. Then the four remaining potentially IR active modes are split into two degenerate modes each – two peaks overlap at 2715cm-1 and also at 1213cm-1 – this explains the appearance of only 3 of the total 6 vibrational modes of BH3.

GaBr₃ Frequency calculation

B3LYP/LANL2DZ level

Frequency log file DOI:10042/101859

Summary Data	Low modes
	Low frequencies --- -1.4878 -0.0015 -0.0003 0.0096 0.6540 0.6540 Low frequencies --- 76.3920 76.3924 99.6767

Wavenumber	Intensity	IR active?	Type
76	3	Yes	Bend
76	3	Yes (slight)	Bend
100	9	Yes (slight)	Bend
197	0	No	Stretch (sym)
316	57	Yes	Stretch (asym)
316	57	Yes	Stretch (asym)

Questions

By keeping the basis set and the method constant we are able to compare molecules with the same number of atoms. We can then compare relative energies of MO’s and the total energies successfully. If we changed the method or basis set, the level or accuracy in our calculations from molecule to molecule with differ leading to larger differences in our energies. A very small in the au of a molecule can correspond to Kj/mol! If we don’t maintain the method and basis set, our analysis is meaningless. The optimisation calculation, aims to calculate the lowest energy configuration/geometry of the molecule by moving along the potential energy surface until it reaches a gradient of zero – i.e. equilibrium. However it is possible in some cases that the “optimised structure” is in fact a transition state and not the energy minimum – the reason the calculation thinks the transition state is the lowest energy configuration is because it is also a stationary point, the energy doesn’t not change with an infinitesimal change in the spatial arrangement of the nuclei – collectively denoted by R1. Only when an energy minimum is obtained can be say that the system has been truly optimised – this can be checked by running a frequency analysis – interpretation of a frequency analysis tells us two this – first, whether our optimised structure is in fact the lowest energy configuration and information about the IR spectrum and IR active vibrational modes – as seen above with BH3. All positive frequencies confirm that we do indeed have the lowest energy optimised structure.

The lower the low frequencies – the better the calculation being undertaken, the low frequencies represent micro distortions to the optimised molecule. Sometimes running an Opt+Freq calculation can alleviate problems and give rise to the best and most accurate calculation available with a specific method/basis set.

Compare the BH3 and GaBr3 spectrum, why this difference?

Since the B and Ga atoms have interchanged the molecules have differing force constants and different levels of IR frequency is required to cause excitation to the higher vibrational energy level. The larger the wavenumber the greater the energy absorbed and hence the stronger the bond. Comparison of the spectra suggests that the B-H bonds are stronger than Ga-H bonds, something that has already become apparent with our computed bond lengths.

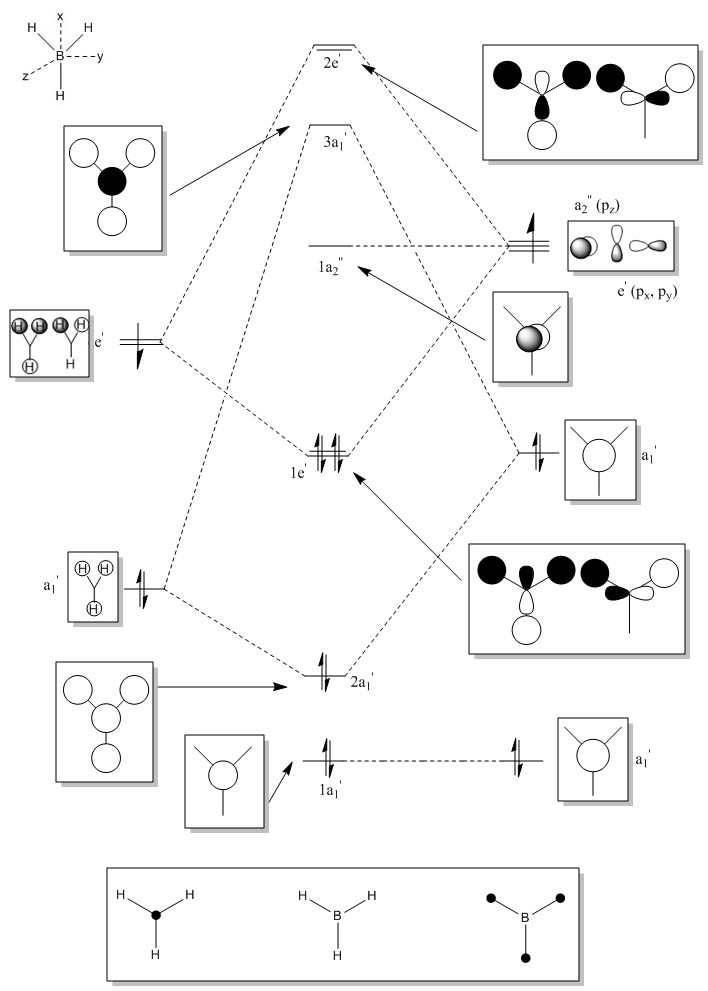
Molecular Orbitals of BH₃

LCAO of BH₃

DOI:10042/104128

It is important to note that since the Atomic orbitals of Boron and Hydrogen fragment orbitals are not degenerate, the resulting LCAO molecular orbitals have unequal contributions from the two consituent orbitals in the linear combination - this may not be well represented on the diagram since the orbitals in our MO constructions dont really vary in size. Usually the bonding orbital has a greater contribution from atomic/fragment orbital which is lower in energy (more electronegative). The inverse is true for the antibonding orbital from the same combination - the higher energy fragment will contribute greater to the antibonding orbital.

Standard rules apply - orbitals can only combine if they are of the same symmetry, the closer in energy two combining orbitals the greater the interactions and the bigger the energy gap between fragments and the molecular orbitals formed.

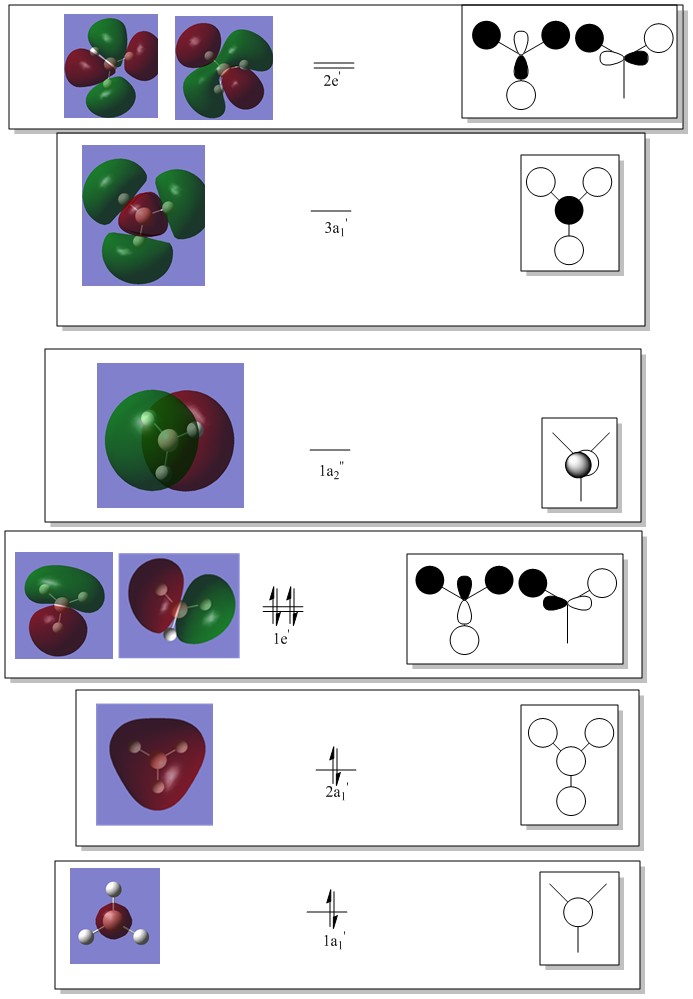
LCAO vs Computed MOs

Note; LHS Computed MO corresponds to LHS LCAO MO for the degenerate bonding MOs

This is inverted for the degenerate antibonding MOs

Commentary and Questions

Upon comparison of our LCAOs and the corresponding computed MOs – it is clear that this qualitative method for predicting molecular orbitals is very effective. The graphical interpretation of the computed MO remain consistent with the proposed LCAO’s wrt nodal planes etc. For the core orbitals upto a few unoccupied orbitals the LCAO is a very good qualitative tool. It is however, always difficult to know the relative contribution of atomic orbitals when using LCAO, only computational MOs reflect this accurately. As we begin to study higher energy unoccupied orbitals the LCAO fails to accurately reflect the “true” (computational) molecular orbital wavefunctions.

In conclusion, LCAO is a valid qualitative tool for determining the nature of molecular orbitals upto to a certain energy level, validating the usefulness of qualitative MO theory. Another issue with qualitative MO theory is that it can fail to accurately predict the ordering of the molecular orbitals - by energy.

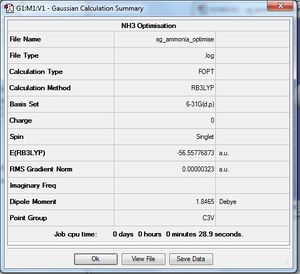
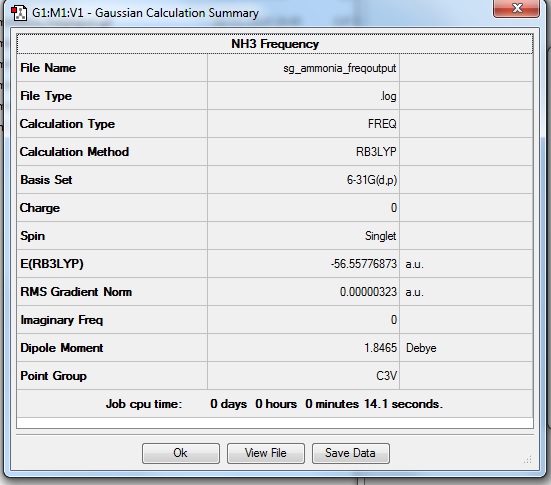
NH₃

B3LYP/6-31G(d,p) Optimisation

DOI:10042/104748

Optimisation log file here

Summary data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000012 0.001800 YES RMS Displacement 0.000008 0.001200 YES	optimised ammonia molecule

Explicitly determined point group of NH₃ is C_3v.

B3LYP/6-31G(d,p) Frequency analysis

DOI:10042/104802

Summary Data	Low modes
	Low frequencies --- -0.0131 -0.0027 -0.0023 7.0724 8.1020 8.1023 Low frequencies --- 1089.3849 1693.9369 1693.9369

Wavenumber	Intensity	IR active?	Type
1089	145	Yes	Bend
1694	14	Yes (Very slightly)	Bend
1694	14	Yes (Very slightly)	Bend
3461	1	No	Stretch
3590	0	No	Stretch
3590	0	No	Stretch

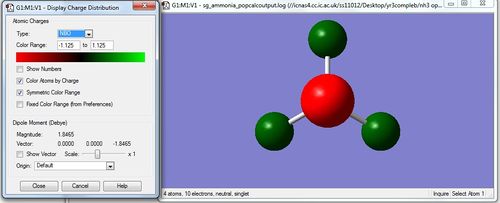
NH₃ NBO analysis

DOI:10042/104852

Atom	Charge
Nitrogen	-1.125
Hydrogen	0.375

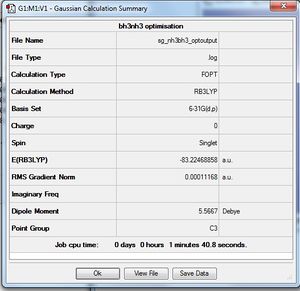
NH₃BH₃

B3LYP/6-31G(d,p) Optimisation

DOI:10042/104965

Summary data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000233 0.000450 YES RMS Force 0.000083 0.000300 YES Maximum Displacement 0.001201 0.001800 YES RMS Displacement 0.000370 0.001200 YES	optimised ammonia borane molecule

Point group of NH₃BH₃ should be C_3v.

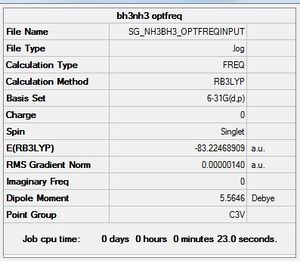
B3LYP/6-31G(d,p) Frequency analysis

Frequency file: here

Summary Data	Low modes
	Low frequencies --- -5.1229 -2.4390 -2.4259 -0.0010 0.0221 0.1790 Low frequencies --- 263.3148 633.0321 638.4701

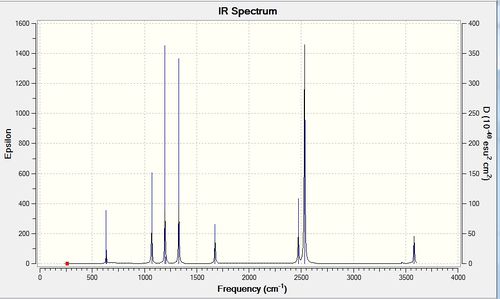
Wavenumber	Intensity	IR active?	Type
263	0	No	Bend
633	14	Yes	Stretch
638	4	No	Bend
638	4	No	Bend
1069	41	Yes	Bend
1069	41	Yes	Bend
1196	109	Yes	Bend
1204	3	No	Bend
1204	3	No	Bend
1329	114	Yes	Bend
1676	27	Yes	Bend
1676	28	Yes	Bend
2472	67	Yes	Stretch
2532	231	Yes	Stretch
2532	231	Yes	Stretch
3464	3	No	Stretch
3581	28	Yes	Stretch
3581	28	Yes	Stretch

Questions

E(NH₃) = -56.5577687 au

E(BH₃) = -26.6153236 au

E(NH₃BH₃) = -83.2246886 au

ΔE=E(NH₃BH₃)-[E(NH₃)+E(BH₃)] = -0.0515963 au

-0.0515963 au = -135.47 kJ/mol

Our computations suggest that the N-B bond in ammonia borane has a dissociation energy of +135 kJ/mol, with respect to other known bond energies, this bond can be categorized are relatively weak.

Aromaticity Project

All molecules in this project we calculated upon using the same method B3LYP and basis set of 631G9(d,p), this is important as it allows comparison of the iso-electronic optimized structures.

Calculation links - DSpace

Computations

Calculation	Benzene	Boratabenzene	Pyridinium	Borazine
Optimisation	DOI:10042/106794	DOI:10042/107287	DOI:10042/107281	DOI:10042/107275
Frequency	DOI:10042/106829	DOI:10042/107285	DOI:10042/107279	DOI:10042/107273
MO/NBO	DOI:10042/106890	DOI:10042/107283	DOI:10042/107277	DOI:10042/107271

Optimisation

Optimisation

	Summary	Convergence	Jmol
Benzene - the reference		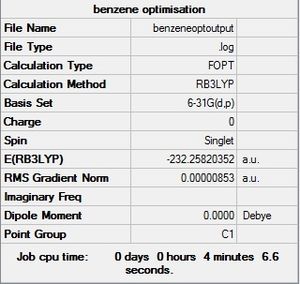Maximum Force 0.000013 0.000015 YES RMS Force 0.000004 0.000010 YES Maximum Displacement 0.000054 0.000060 YES RMS Displacement 0.000017 0.000040 YES	optimised benzene molecule
Boratabenzene		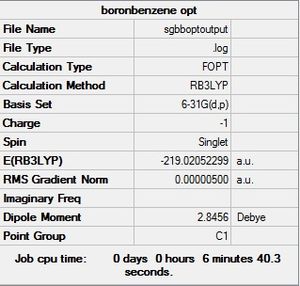Maximum Force 0.000010 0.000015 YES RMS Force 0.000002 0.000010 YES Maximum Displacement 0.000045 0.000060 YES RMS Displacement 0.000013 0.000040 YES	optimised boratabenzene molecule
Pyridinium		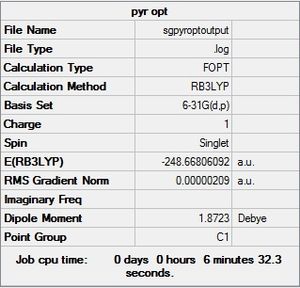Maximum Force 0.000004 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000012 0.000060 YES RMS Displacement 0.000004 0.000040 YES	optimised pyridinium molecule
Borazine		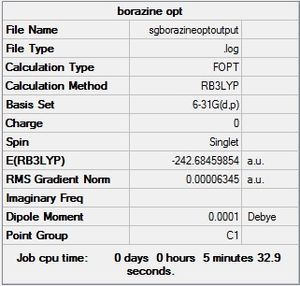Maximum Force 0.000083 0.000450 YES RMS Force 0.000033 0.000300 YES Maximum Displacement 0.000252 0.001800 YES RMS Displacement 0.000077 0.001200 YES	optimised borazine molecule

Frequency

Frequency

	Summary	Low modes
Benzene - the reference		Low frequencies --- -10.1273 -5.4307 -5.4307 -0.0055 -0.0055 0.0003 Low frequencies --- 414.5511 414.5511 621.0436
Boratabenzene		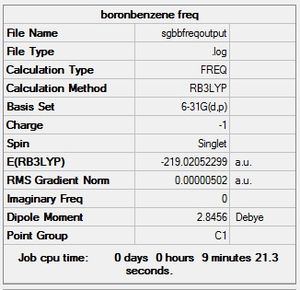Low frequencies --- -7.2712 -0.0005 0.0005 0.0011 3.1485 4.5187 Low frequencies --- 371.2965 404.4156 565.0825
Pyridinium		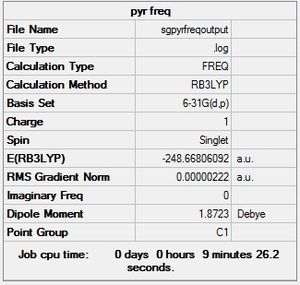Low frequencies --- -9.3872 -2.9468 0.0006 0.0009 0.0011 0.8142 Low frequencies --- 391.9004 404.3425 620.1995
Borazine		Low frequencies --- -3.9535 -1.5465 -0.0004 -0.0003 0.0007 1.6756 Low frequencies --- 289.4961 289.6331 404.3473

All four molecules were successfully optimised. Frequency calculations were also carried out and confirmed that all four optimised structures were in fact minima. Energy calculations can now be carried out on these optimised molecules, this computes the MOs and allows us to carry out NBO charge analysis. Comparison of the NBO charge distribution and the MOs forms the interesting part of this project.

NBO charge analysis

gaussview interpretation of nbo data (1.102 - +1.102 colour limits)

benzene	boratabenzene	pyridinium	borazine

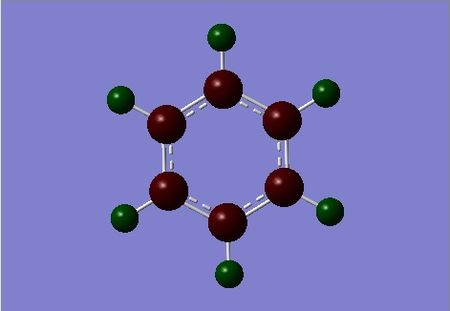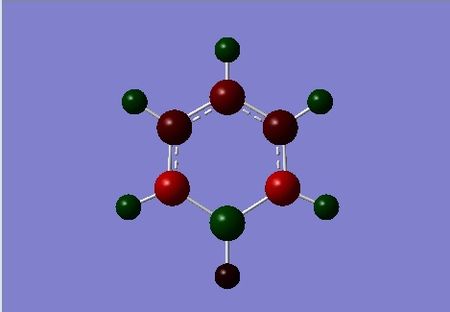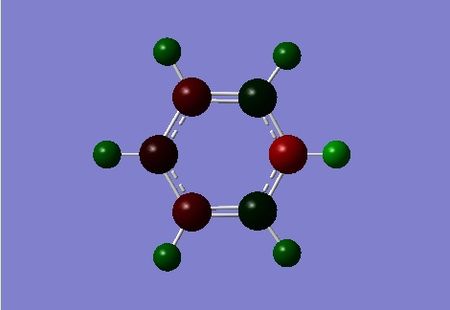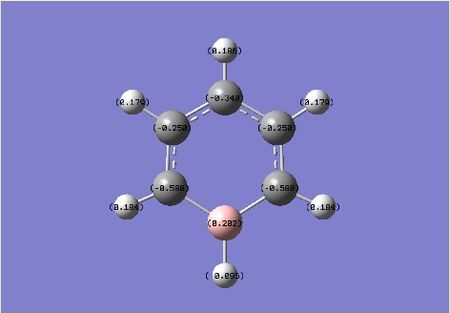
Differences in the electron density on each atom can be explained by the atom's electronegativity – its tendency to attract and its affinity for a pair of electrons. Benzene being symmetric has uniform electron density over all its carbon and hydrogen atoms respectively. From the figure above we can see that the carbon atoms in benzene have a charge of -0.239 with the hydrogen’s exhibiting a charge of equal and opposite magnitude. This confirms that the carbon is in fact more electronegative than hydrogen, confirmed by the Pauling scale of electronegativity. Literature values on the Pauling scale show an E-neg difference of 0.350 for Carbon relative to hydrogen, this is consistent with the NBO charge distribution computed from our optimised structure.

When we move from Boron to Boratabenzene we reduce some symmetry and the remaining carbons no longer have an equally disturbed level of electron density. Boron is less electronegative than both Carbon and Hydrogen. The Carbon atoms within the ring have an even larger affinity for electron density relative to boron atoms. The interesting point it notice is that, the Carbon atoms adjacent to the Boron are more negatively charged than previously. The para carbon is also more negatively charged at a value of -0.348 in comparison to its adjacent carbons at -0.250 (meta). This could be explained by the fact that there is a formal negative charge on this complex. This negative charge could be alternating on the othro and meta positions, easily shown by resonance forms of this anion.

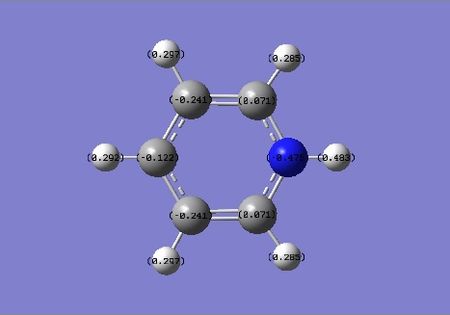
The isoelectronic pyridinium contains the most electronegative atom in our any of our three benzene analogues. It is expected that the nitrogen atom has the largest negative charge of any atom in within the cation, the NBO analysis confirms this, the value being -0.476. In contrast to Boratabenzene, pyrdinium carries a net positive +1 charge. In this case the carbons at position 3 and 5 are have a charge value of -0.241, whilst the position 2 and 4 are more positive at 0.071 and -0.122. The position adjacent to the Nitrogen is the most positive carbon due to its close proximity to the nitrogen atom, but also because resonance forms can formally place the net +1 charge at the positions 2, 6 and 4 (othro and para).

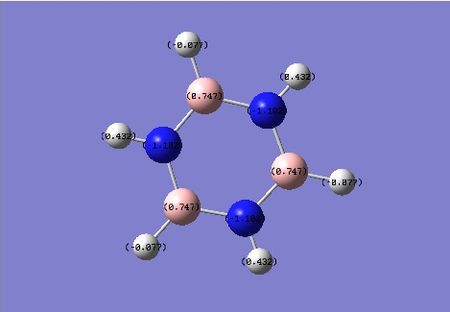
Borazine has a highly symmetric nature due to alternating electronegative nitrogen and electropositive Boron atoms. With the very large electronegativity gap between these atoms we should expect these nitrogen atoms to be the most electron density rich and the adjacent boron atoms to been the most electron density poor atoms across all four molecules, and this is certainly the case. The charge colour diagrams clearly represent this. On Borazine, the nitrogen atoms have a value of -1.102 whilst the alternating boron atoms have a value of 0.747.

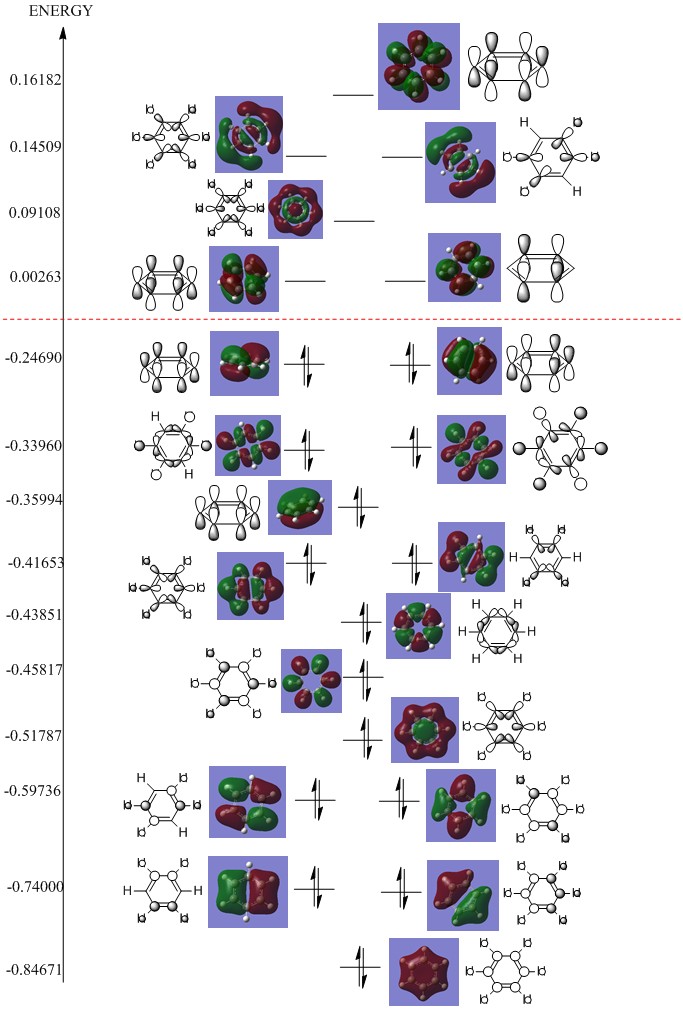
Deconstruction of Benzene's computed MOs into a LCAOs

How do these MOs relate to the common conception of aromaticity? Hint 2: aromaticity relates to delocalisation. Hint 3: aromaticity relates to the total pi electron density, and MOs contain formally only 2 electrons each.

According to Huckel’s rule, 4n+2, Aromatics require either 6, 10, 14 etc pi electrons to be classed as aromatic. The common conception of aromaticity is that of cyclic delocalisation of electrons above and below the face of the molecule, this gives rise to increased stability, more than expected. Delocalised electrons are free and extended over the face of the cyclic molecule with the electron density usually found above and below the plane holding the sigma framework. From our computed MO orbitals it is very easy to confirm the aromatic electronics of benzene. Orbitals 21, 17 and 20 represent the MO’s responsible for Benzene’s bonding-favouring aromaticity. The three orbitals are with other antibonding pi based orbitals, are made up of the basis set of perpendicular p orbitals from each carbon atom. This basis set allows for the formation of molecular orbitals that extend above and below the sigma framework giving rise to the regions of delocalised pi electron density. Since these are the only pi based orbitals which are occupied we can confirm that Benzene is consistent with Huckel’s rule when n=1.

Comparing MOs

1st MO - pi totally bonding (17)

benzene	boratabenzene	pyridinium	borazine
-0.35994	-0.13210	-0.64062	-0.36130

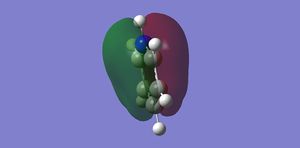
Orbital 17 – This pi MO can be constructed by (LCAO) 6 in phase p orbitals, which are all perpendicular to the plane of benzene. This orbital is one of a few that gives benzene its aromatic characteristics. We expect the MO to be highly symmetric containing a nodal plane within the plane of the sigma framework, this is certainly the case. The energy of this orbital is given as -0.35994 au, which will later be compared to the other 3 molecules. The same orbital in Boratabenzene has an energy of -0.13210 au, being more unstable in comparison to the benzene orbital, this can be explained by applying LCAO. Previously all 6 p orbitals used to construct orbital 17 in benzene were completely degenerate, this optimised the interaction of the AO’s wrt to their energies and sizes. In Boratabenzene, one of the p orbitals have now been replaced by a relatively higher energy non degenerate p orbital. Clearly the size match and energy matching of this boron p orbital with the adjacent carbon p orbitals is not as effective as in benzene. This makes for a less promising interaction, hence the energy of this orbital is higher. Since the MO in question is a bonding MO, the contribution from the boron’s p orbital will be slightly lower than in comparison to the carbon’s p orbitals. This is evident from the nature of the MO, the snapshot clearly shows a decrease in electron density near the region close to the Boron atom. Since the same in phase set of AO are used in the linear combination, we still expect the same nodal plane through the sigma framework of this molecule, which is very clearly seen. The same orbital in pyridinium has an energy of -0.64062, being lower than both benzene and Boratabenzene. Once again as with the previous two, the orbital is also non-degenerate. The expected single nodal plane is present and the relatively electronegative and low energy p orbital of nitrogen makes a greater contribution compared to the other AO’s used in the LCAO. The MO graphic clearly shows the inverse in the skewing of molecular density in comparison to Boratabenzene. Borazine’s all bonding pi orbital is very similar to benzene but which more electron density in the vicinity of the Nitrogen atoms.

2nd MO - Carbon 2s and Hydrogen 1s in phase MO (7)

benzene	boratabenzene	pyridinium	borazine
-0.84671	-0.60437	-1.21399	-0.88851

Orbital 7 – Is the first non-core like orbital, and in Benzene we have what you’d expect, a completely in phase region with 2S and 1S orbitals being using in the LCAO. We expect no nodal places and each AO used in the LCAO is in phase. The energy of this orbital being -0.84671, the corresponding in boratabenzene has an energy of -0.60437. The less stability can be explained by the fact that we are replacing a carbon with a boron, the boron orbital contributes considerably less and it is evident from the computation’s diagram. The energy difference in the fragments forming the MO gives rise to less effective orbital overlaps and hence a weaker interaction, this explain why this orbital is higher in energy compared to the benzene analogue. Once again for pyridinium’s first non-core orbital we expect a greater contribution from the nitrogen 2s to the overall MO in comparison to the carbon 2s orbitals, the computed MO showed a skew of electron density towards the nitrogen, supporting this claim. This is logical since the very electronegative nitrogen’s 2s is relatively low in energy and hence contributes the most to the bonding MO. This orbital is more stable compared to the benzene’s corresponding AO with an energy of -1.21399. Borazine computations show a highly symmetric orbital for 7, with a greater amount of electron density on the nitrogen, this orbital is expected to be the highest in energy of the number 7 orbitals simply because of the large energy gap between the boron and nitrogen p orbitals, and this extended gap gives rise to a less effective linear combination.

3rd MO - HOMO (21)

benzene	boratabenzene	pyridinium	borazine
-0.24690	0.01095	-0.47886	-0.27590

HOMO – The HOMO of benzene can be depicted with a LCAO of perpendicular p orbitals on each member of the ring, three being in phase and three being out of phase. This gives rise to the additional nodal plane perpendicular to the sigma framework. The energy of this orbital is computed to be -0.24690. The energy of the Boratabenzene HOMO is 0.01095, higher than the HOMO of benzene making this molecule more susceptible to electrophilic attack. The same nodal planes remain. The HOMO in pyridinium is at an energy of -0.47886 making this more stable than benzene, its seems from the computed MO that the ordering of MO’s has perhaps changed, a LCAO using only 4 perpendicular p orbitals could be used to construct this MO. The lower energy of this homo makes it very unreactive towards electrophiles, as expected for a positively charged species.

<references> </references