Rep:Mod:ss11012MgO
The Free Energy and Thermal Expansion of MgO
Intro
MgO is an "ionically" bonded lattice consisting of Mg2+ and O2- ions. It structure is analogous to that of NaCl face centered cubic/octahedral holes filled),commonly known as rock salt. The crystal structure of MgO can be described by the unit cells shown in figures 1, 2 and 3. Figure 1 represents a face centered cubic bravais lattice, in which the octahedral holes are occupied by O2- ions. The formula unit of MgO is represented by the primitive rhombohedral cell shown in figure 2. In this experiment, computational methods are used to examine the thermodynamic (free energy) and physical properties (structure) of an MgO crystal.
| fig 1 - conventional | fig 2 - primitive | fig 3 - supercell |
|---|---|---|
 |
 |

|
The experiment involves the use of two simulation methods: Lattice dynamics (Quasi-Harmonic approximation) and Molecular dynamics.
Both are used to compute the thermal expansion coefficient, α, of MgO. The results obtained via both methods are
compared/evaluated against each other and peer reviewed literature. The experiment provides an insight into how the material
expands upon heating as well as free energy changes.
α = (1/V0)*(dV/dT)P
Lattice dynamics, the first of the simulation methods, makes use of the Quasi Harmonic approximation. It involves a summation over the quantum based phonon modes of the periodic solid under test. MD simulation involves the evolution of a system gives random initial geometries/velocities collectively corresponding to the required temperature, the big distincion being than anharmonic effects within the crystal, particularly at high temperatures are taken into account.
The experiment makes use of DLVisualise, a graphical user interface along this GULP - the General utility lattice program simulation code. In order to compute energies, the very simple buckingham potential is used throughout the experiement - it neglects (has no terms for) polarisability/covelent character within the crystal.
Part 1 - Initial calculation on MgO
Table 1 -Cartesian lattice vectors (Angstroms) :
0.000000 2.105970 2.105970
2.105970 0.000000 2.105970
2.105970 2.105970 0.000000
Table 2 -Cell parameters (Angstroms/Degrees):
a = 2.9783 alpha = 60.0000
b = 2.9783 beta = 60.0000
c = 2.9783 gamma = 60.0000
Table 3 - Binding energy components :
Interatomic potentials = 6.72119980 eV
Monopole - monopole (real) = -5.11592628 eV
Monopole - monopole (recip)= -42.68059111 eV
Monopole - monopole (total)= -47.79651739 eV
Total lattice energy = -41.07531759 eV
Total lattice energy = -3963.1403 kJ/(mole unit cells)
An initial single point GULP calculation was preformed on the primitive rhombohedral unit cell, the key results are summarised in tables 1-3. The cartesian lattice vectors, shown in table 1, collectively form the primitive cell's vertices. Table 3 provides the lattice parameter(s)/angles, essential information required to define any unit cell spatially. Even though the primitive cell is the smallest cell required to create an macroscopic structure, the cubic cell is more commonly used in crystallographic study. Although the conventional cubic cell (FFC for MgO) is 4x greater in volume, it more accurately reflects the true geometry of an MgO crystal - as shown in figure 1.
Of more interest is table 3. Using the simple Buckingham potential, described in the introduction, the single point calculation computed "Total lattice energy" of the crystal - -41.0753 eV/per primitive cell. This value reflects the strength of electrostatic interactions in an ionically bonded system. The Total lattice energy can be defined as - the energy change when the ions (infinitely far apart/gas phase) translate closer/and are orientated in the manner shown in figure 2, the primitive cell (forming solid ionic MgO). The +ve "version" of this value represents the binding energy - which is defined as the energy required to pull the ions of the crystal to infinite separation. I believe there may be some conventional confusion for this in the lab instructions?
Part 2 - Phonon modes of MgO
Within this experiment we use the Lattice dynamics simulation to model the Thermal expansion of MgO - this requires the Quasi harmonic approximation. We make use of the Quasi harmonic approximation to optimise the structure of MgO at various temperatures - enabling us to see how it changes with temperature - the aim of the experiment. In the "QH" approximation, the free energy, and hence optimised geometry, calculation involves a sum over the phonon modes of the crystal. Before modelling the thermal expansion using LD is even though about, the phonon DOS of MgO, must first be computed.
The Phonon dispersion for MgO was also computed - this is shown in figure 4. This phonon dispersion is calculated along the conventional, WLGWXK k space pathway. Each point on the graph corresponds to a known k space wave vector defined by kx, ky and kz. The phonons were computed for 50 k space points (N points) along this path.
If we sum all the states at a particular frequency over all of k space, we can produce a simplier "energy level diagram" known as the density of states. The phonon density of states provides, the number of phonon modes at a given frequency (energy) over all of k space. The energy of each phonon mode can is accesible, if we use quantum oscillator treatment - E=hv, where v is the frequency of the phonon mode. If we know the distribution of the number of phonon modes over as the frequency varies, we will later be able to compute free energies under the quasi harmonic approximation, which makes use of this DOS summation. The DOS computation is approximated over a select sample of k points, defined by the k space grid used - known as the Monkhorst1 method. The simplest DOS calculation uses a single k point - denoted by the 1x1x1 grid. Figures 5-10 shown the Phonon DOS graphs for increasingly denser grids, ranging from 1x1x1 to 32x32x32. Ideally, to obtain the "true" energies and physical information, and infinite grid covering all k points would be used - A infinite grid would give us perfect accuracy. The problem is that an using an infinite grid would also take infinite time/computer effort. We aim to use an adequetely dense grid, we were recognise some form of convergence, hence why this is an approximation! There is a clear compromise between accuracy and CPU time, we can find the appropriate balance by studying the DOS plots.

 |
 |

|
| fig 5 - 1x1x1 grid | fig 6 - 2x2x2 grid | fig 7 - 4x4x4 grid |
 |
 |

|
| fig 8 - 8x8x8 grid | fig 9 - 16x16x16 grid | fig 10 - 32x32x32 grid |
Figure 5 shows the 1x1x1 grid DOS, this was computed by using a sample of just a single k point. By studying the associated LOG file, this k point is found to be (0.5, 0.5, 0.5) in real space and (π/a, π/a, π/a) in k space. This is also the point L along the WLGWXK pathway in the Phonon dispersion. Looking at Point L on the Phonon dispersion (figure 4) we can see 4 phonon modes - with frequencies at approx. 290, 350, 680, 800 cm-1. The 1x1x1 DOS shows 4 peaks at the same frequencies - this is consistent with, and confirms the k point as the symmetry point L.
As we increase the grid size, more and more k points are incoporated into the DOS calculation. At less denser grids such as 1x1x1, 2x2x2 and 4x4x4 we see discrete spikes along the frequency range, as we continue to increase the grid size to 8x8x8 onwards we begin to see a continuous smooth function appear. This graphical change is because as we increasing the grid size we are incorporating more and more k points (not linearly but higher order), giving a more accurate DOS function. Lets consider Point L, if we just used this point at looked at the 650 cm-1 region on the DOS, we can expect a single sharp spike at corresponding to the single phonon mode we are constrained to - we have neglected the fact that at L+dK, we also have other phonon modes present, these are not accounted for on the 1x1x1 DOS - very inaccurate. If we now considered the k point L+dk, using a denser grid, we would find a more broad peak around the 650 cm-1 region of the DOS - as seen with the more dense grid sizes.
In order to find an appropriate grid size whilst making sure the CPU demand remained feasible - the DOS calculation was computed using the 1x1x1 grid and then doubled until the final 32x32x32 grid calculation, it is important to note that by doubling the grid size, and maintaining it as "even", we insured that we were sampling additional k points whilst including all of the previous sample set. The choice of the which grid size is reasonable has two consideration, has the calculation began to converge in its solutions? and by how much is the computational demand increasing as be double subsequent grids? When we compare the visual DOS plot, it is apparent that plots change most significantly in the first few lower density grid changes (1x1x1 to 2x2x2 to 4x4x4 to 8x8x8). Once the 8x8x8 calculation is computed we obtained a much broader looking plot compared to previously, the change from 8x8x8 to 16x16x16 further smoothens the plot, with the 32x32x32 being effectively identical to the 8x8x8 plot when examined by the naked eye, this indicates convergence to the "true" DOS plot - if we had used an infinite sample of k points. We can confirm this convergence upon examination of table 4 (irrespective of the fact these calculations were at 300K). The same grid sizes in the phonon DOS calculation were then also used to compute the free energy at 300K. From table 4 - we can see that when we move from 8x8x8 to 16x16x16, the deviation in the "Free energy" is -4.000 x 10-6 eV. When we move from 16x16x16 to 32x32x32, the deviation in free energy is -1.000 x 10-6 eV. For the purposes of this experiment the 8x8x8 would suffice (only quoting to 4dp) since its deviation is minimal when moving to the 16x16x16, the deviation to the 32x32x32 grid being even smaller, this shows convergence to a "true" value. We must also consider the computational demand of all these computations, for the purposes of the experiment, the only computation which has inappropriate demand/running time is the 32x32x32 grid calculation. The 32x32x32 grid calculation requires 23.3605 seconds and 41.52 megabytes for its calculation. For the time scale we have and the accuracy we require this is inappropriate. The 16x16x16 grid calculation gives a Free energy value only 1x10-6 eV off whilst using only 1.2417 seconds/5.62 megabytes. The 16x16x16 grid gives a good resolution DOS function, which will help avoid major errors in the thermal expansion results later in the experiments. These calculations can also be run quickly and inexpensively - a 16x16x16 grid was therefore used.
It is also important to consider where this grid size would be for a calculation on different structures ranging from CaO, zeolites (e.g. faujasite) and metals (e.g. lithium). The main difference is the changing unit cell sizes for each of these structures. The larger the unit cells in real space, the smaller the regions (Brillouin zones) in k space - given by a* = 2π/a. This means that for a system with a larger real space cell, the same grid will give significantly greater grid density as the equivalent k space "cell/zone" is smaller. For CaO, a similar grid size should be used, although the unit cell will be slightly larger going from Mg to Ca, the change in real space unit cell size will not be significant enough to change the k space grid density vastly. Faujasite (Zeolites) has a very large real space cell relative to MgO, this meanings the 16x16x16 grid would give rise to very high grid density which is not necessarily required. The grid size could therefore be lowered, as this would still give adequete results whilst also decreasing CPU demand/times even further. For metals such as Lithium, using the same idea as above, the Unit cell of lithium is much smaller than that of MgO, this results in the need of a larger grid to maintain the grid density in k space.
Part 3 - Quasi-Harmonic Approximation
| grid size (k-space) | Free energy (eV/primitive cell) | ΔE (eV/primitive cell) from previous grid | CPU demand (seconds, megabytes) |
| 1x1x1 | -40.9303 | n/a | 0.0037, 0.48 |
| 2x2x2 | -40.9266 | 3.692 x 10-3 | 0.0052, 0.51 |
| 4x4x4 | -40.9265 | 1.590 x 10-4 | 0.0168, 0.58 |
| 8x8x8 | -40.9265 | -2.800 x 10-5 | 0.1280, 1,13 |
| 16x16x16 | -40.9265 | -4.000 x 10-6 | 1.2417, 5.62 |
| 32x32x32 | -40.9265 | -1.000 x 10-6 | 23.3605, 41.52 |
Table 4 above shows the LD - free energy calculation at 300K. The ΔE (eV/primitive cell) from previous grid column shows how the Free energy varies when doubling the grid size and hence increasing the grid density. From Table 4 is it clear that when changing from the lower to the higher grid sizes, the Free energy does not converge in the same direction every time (not always a positive deviation or a negative deviation). For example when moving from 2x2x2 to 4x4x4, the change in energy was 1.590 x 10-4 eV. When moving from 4x4x4 to 8x8x8, however, the energy change was -2.800 x 10-5 eV. The difference in Free energies when moving from 8x8x8 to 16x16x16 to 32x32x32 became smaller and smaller - suggesting convergence to a "true value", indicate that the grid size is sufficient enough to produce high levels of accuracy.
From the deviations above, as we more from one grid size to another we can find the appropriate grid size required for accuracy to 1, 0.5 and 0.1 meV.
Calculations accurate to 1meV are appropriate on a 2x2x2 grid. Calculations accurate to 0.5 meV are also appropriate on a 2x2x2 grid. Calculation accurate to 0.1 meV require a 4x4x4 grid, and perhaps a 3x3x3 would suffice however, this was not tested over the course of the experiment. Another method requires seeing the deviation off all grid sizes relative to the 32x32x32 grid, which for arguments sake can be considered the "truest value" and the appropriate grid could also be calculated by considering the deviation of each grid to this one (the 32x32x32).
The optimum grid size for CaO, Faujasite and Lithium would follow the same trend outlined in the previous section - For e.g. for CaO we should use a similar grid size since the real space unit cell is also similar in size, we can also expect a similar convergence. The grid sizes should be varied according to the real space cell size, as outlined in the previous section.
Part 4&5 - Thermal Expansion of MgO
Quasi-Harmonic approach
Within this section we optimise the structure of MgO by finding the lowest free energy at a given temperature and pressure. This Free energy is once again computed within the Quasi-Harmonic approximation. Throughout this simulations, the pressure is kept constant allowing us to model how the structure changes (expands) solely as a function of temperature.
Figures 11 and 12 - show the Free energy and lattice parameter dependence on temperature under the Quasi-Harmonic approximation. From figure 12 - it is evident that the cell size/dimensions are expand with raising temperature. As we increase the temperature the magnitude of vibrations within the crystal also increases, this results in the average distance between adjacent lattice points over a given period of time, to also increase, this explains why the lattice parameter increases in size. The plot confirms that as the temperature is raised, the system thermally expands.
Figure 11 shows the variance of the Gibbs free energy as a function of temperature. With increasing temperature, decreasing Gibbs Free energy is observed. The Gibbs free energy is defined as G=H-TS. Differentiating wrt to temperature (constant pressure) gives dG/dT=-S, the plot is consistent with this equation and hence expected thermodynamically. The plot however does not give a straight line, but in fact is a curved function, this is because the entropy is in itself dependent on temperature, and becomes larger at higher temperature - hence why the second derivative of the slope becomes increasingly negative (larger negative gradient) with increasing temperature.
 |

|
| fig 11 - Free energy vs temperature | fig 12 - Lattice parameter v temperature |
 |
|
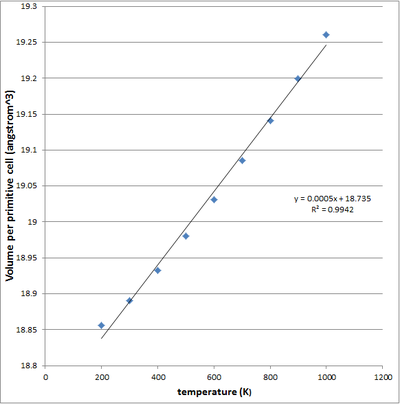
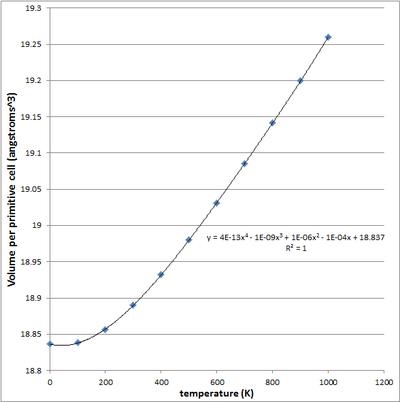
| fig 13 - Cell volume v temperature (linear) | fig 14 - Cell volume v temperature (4th order polynomial) |
| V0 (Angstroms3) | Temperature (K) | α (K-1) - using linear trendline | α (K-1) - using polynomial trendline | α (K-1) - literature |
| 18.8365 | 100 | 2.6544 x 10-5 | 3.8011 x 10-6 | |
| 200 | 2.6544 x 10-5 | 1.0235 x 10-5 | ||
| 300 | 2.6544 x 10-5 | 1.4504 x 10-5 | 3.12 x 10-5 | |
| 400 | 2.6544 x 10-5 | 1.7116 x 10-5 | 3.57 x 10-5 | |
| 500 | 2.6544 x 10-5 | 1.8581 x 10-5 | 3.84 x 10-5 | |
| 600 | 2.6544 x 10-5 | 1.9409 x 10-5 | 4.02 x 10-5 | |
| 700 | 2.6544 x 10-5 | 2.0110 x 10-5 | 4.14 x 10-5 | |
| 800 | 2.6544 x 10-5 | 2.1193 x 10-5 | 4.26 x 10-4 | |
| 900 | 2.6544 x 10-5 | 2.3168 x 10-5 | 4.38 x 10-4 | |
| 1000 | 2.6544 x 10-5 | 2.6544 x 10-5 | 4.47 x 10-4 |
Using the Log files for the simulation at all these temperature, we can quantitatively describe the thermal expansion process - by the Thermal expansion coefficient, α. α is defined as (1/V0)*dV/dT. (1/V0) denotes the initial volume of the system (primitive cell) at 0K, whilst dV/dT denotes the rate of change of the volume wrt to temperature - keeping pressure constant. From the calculation LOG files, it is possible to plot the optimised volume of the cell at each temperature. Differentiating this function, gives the dV/dT(T) function which could then be evaluated at each temperature. The thermal expansion coefficient is then compared to literature values. Both a linear and a 4th order plot were used in the α computation, this plots are shown in figures 13 and 14. The calculation thermal expansion coefficients using both plots are given in Table 5 - with reference to peer reviewed literature2.
From the literature it is evident that the expansion coefficient is not constant over all temperatures but is in fact increasing with temperature - there is no need for α v temperature plots are this is quite clear from table 5. Our thermal expansion coefficient is a constant when modelled using the linear fit, shown in figure 13. From the literature values we can confirm that in reality this is not the case. In reality the thermal expansion coefficient is not constant but varies with temperature, for this reason a 4th order polynomial fit was also applied to the data, giving a coefficient of determination R2 of 1. Using this we were able to obtain gradient at each and every temperature, one would expect that this would give a much better approximation for α values at each temperature. From table 5 - it is apparent that both methods showed deviation from the literature values. It is important to note that for the most part both the linear and polynomial plots produced thermal coefficients with the same order as the literature readings, this reflects some level of accuracy within our simulation method. For each temperature over the 0K-1000 range, the α from the linear plot showed a smaller deviation from the literature when compared to the polynomial computed α - this suggests that the linear method best fits the literature. What the polynomial based computation for α do show, however, is the temperature dependency of α. Although the α range over the temperatures is skewed lower than the literature, it still is able to show the increasing that the thermal expansion coefficient is in fact increasing with temperature. The literature readings show that at higher temperatures, the volume increases by a greater extend for an infinitesimal increase in temperature when compared to lower temperature - this is something we should look out for through the experiments.
The physical origin of thermal expansion can be explained by considering the extent of vibrations within the crystal. As we increase the temperature, the phonon population of the crystal also increases - additional higher energy states are activated/excited to thermally. The greater the oscillations, the greater the average distance between ions in the unit cells, and hence an increase in volume (thermal expansion). It is important to note that the cells are not constrained to the calculated volumes from the calculation. In reality, at any one snapshot of time we may have a deviation from this volume due to vibrational effects.
As we approach the melting point of MgO, we can expect the Quasi harmonic approximation to deviate from the actual phonon modes of the crystal. The key point here is that, it is assumed within the QH approximation that the phonon modes do not interact with each other, in reality we most consider phonon-phonon interactions. Phonon modes are able to interact with each other, and these interaction become more significant at higher temperatures - when phonon modes interact, certain phonon modes computed by our simulation in fact decay into other modes, this is not accounted for within our simulation, and we may therefore not actually represent the actual phonon modes of the crystal. This becomes more important at higher temperature, this is because the population over the phonon range increases (thermal broadening effect), resulting in an increased probability of interaction between different phonon modes.
The harmonic potential is a symmetric function, at higher temperatures the equilibrium point remains constant at the bottom of the well, but we begin to exhibit higher order oscillations in bond length about this point - the equilibrium bond lenght does not actually change, since we cannot move out of the parabolic well - this is harmonic oscillation. To describe the increasing bond length in a solid we in fact require an asymmetric potential - MD accounts for this
Molecular Dynamics approach
The Molecular dynamics simulation requires probing of the MgO 32 formula unit super cell, this is shown in figure 3. This cell is quite easily constructed by repeating the conventional cubic cell along each lattice axis twice. We could also use a even larger supercell, this way the actual computation this would in fact give rise to more accurate results, the compromise being increased CPU time/demand. We also the system to evolve in time according to Newtown's second law, F=ma - we assign random initial velocities/configurations to each ion within the crystal, which collectively correspond and mimic the temperature under consideration. We then compute properties are time averages with a time step of 1 femtosecond. The average data was taken at the end of the computation. Throughout the simulation, the on going average was recorded after computating how the system had evolved at each interval. This method applies F=ma, with the underlying forces being modelled by the simple Buckingham potential previously described. Results from the MD dynamics simulation, as well as the LD simulation are given in table 6 and figure 15 - the simulation we done over the 100-3000K range, it is important to understand how the volume varies across all temperatures the MgO remains solid. It is now possible to compare the thermal expanision model proposed by both Lattice Dynamic and Molecular Dynamics. Since the MD simulation assigns random initial configurations/velocities, there is an implicit error in each result, repeat calculations were performed to define these errors, this is shown by the error bars for the MD plot in figure 15.
 |

|
| table 6 - Thermal expansion data (QH vs MD) | fig 15 - Cell volume vs Temperature (QH vs MD) |
The data in table 6 shows the calculation of thermal expansion coefficients over the 100-3000 K temperature range. For both LD and MD, a 4th order polynomial fit was used to compute dV/dT in the α computation. In both cases the 4th order polynomial functions best fit the plot profiles, giving R2 values of 0.99 to 2.d.p in both cases. Alternatively a 2nd order polynomial function for both would have also been sufficient.
Both the LD and MD are in close agreement in terms of the profile of the volume v temperature plots, especially at the lower temperatures. At higher temperatures both deviate from each other, something discussed later in the text. The thermal expansion coefficients were computed so that they could be compared to literature, assessing the validity of our measurements - peer reviewed literature values we obtained for the 300-2000 K range3. From this point onwards the 300-2000 K range will be referred to as the "literature" range. Over the literature range is it apparent that there is some form of systematic error in the computed expansion coefficients - irrespective of this deviation from the literature, coefficients obtained from the literature, MD and LD were of the same order of magnitude - this confirms some degree of accuracy within the results. The deviation from literature can be explained by the various approximations in our simulations - the level of grid density in our LD simulation and the random initial configurations/velocities in our MD simulation. Irrespective of this error, both the LD and MD data, outlines trends seen in the literature range. Over the literature range, the literature shows ever-increasing expansion coefficients. For LD, the expansion coefficient is also increases for each subsequent temperature for the most part, ignoring a few points. MD failed to show this trend over the temperature range, and if fact computed a larger expansion coefficient at 300 K compared to 2000 K, this does not reflect the peer reviewed literature ("reality"). This trend in the literature would manifest itself as a gradient becoming more and more steeper on the volume v temperature plot - the LD function reflects this to an extent, whereas MD shows almost a small "random" deviation in dV/dt from start to finish over the entire range. It is important to note that discussion of expansion coefficients, is also implicit discussion of the volume v temp plots profiles themselves.
At the earlier temperatures within the "literature range" - we have much closer agreement of the LD/MD values to the literature. Towards the end of the literature range the deviation from literature of both LD/MD is much more significant. e.g. @ 2000K MD - 2.44 x 10-5, LD 2.87 x 10-5 and lit - 5.33 x 10-5. We can explained this graphically, as the temperature increases the rate of change of the much higher for the literature readings in comparison to the simulation readings. If the raw literature volume v temperature graph was plotted it would start to come more and more steeper much earlier than compared to the simulations. This causes the increasing deviation from the literature for both LD/MD across the "literature range". Throughout the "literature" both LD and MD show relatively closer agreement. When considering the absolute volumes per formula unit, it is important to recognise that the LD over nearly all temperatures predicts a larger volume than the corresponding MD volume - as shown in table 6.
The two methods both produce different results, which vary more/less significantly from on another depending on temperature. These differences can be explained by considering the differences in the methodology of both simulations including the approximations made in both. Firstly, Lattice dynamics makes use of Phonon DOS function, by summing over the phonon modes in the simulation. This incorporates quantum effects and at low temperatures both the volumes from LD and MD are in close agreement. At very high temperatures, near to the melting point of the MgO (3125.15 K)4, the LD simulation breaks down. The Quasi harmonic approximation makes use of harmonic symmetric functions, meaning irrespective of being close to melting point, bonds are not allowed to "break". The MD simulation at on the other hand, as low temperatures shows good argeement with LD for volumes/per formula unit. At larger temperatures, nearing 3000K, does not completely break down like LD and takes into account anharmonic effects within the crystal, this allows for "bonds" to break. However, at lower temperatures MD predictions are less accurate since the simulations do not take into account dominant quantum effects2, with LD, however, this is not the case. At lower temperatures, we can be less concerned by the phonon-phonon interactions which are not accounted for by the QH approximation, as they are not as apparent as at higher temperatures.
An over-approximation of the cell volume occurs if we use the LD (QH) simulation at very high temperature, nearing close to the melting point of an MgO crystal. There comes a point, between 2900-3000K (evident by examining table 6) when the Quasi-Harmonic simulation breaks down - this is because it does not take into account the anharmonic effects within the crystal and does not allow bond breaking. In MD, however, does not break down at high temperatures around the melting point, since it accounts for anharmonic effects.
Conclusions
The experiment aimed to model the thermal expansion of MgO using LD and MD, and then contrast and compare these results. In both cases the vibrations of the crystal were modelled using quantum computed phonon modes (LD) or classically (F=ma) by seeing how a system evolved over time. Calculations computing the Phonon DOS at different grid sizes were undertaken to find an appropriate grid size with good accuracy and bearable CPU demand/times - the 16x16x16 grid was chosen. The 16x16x16 Phonon DOS provided the sample of phonon modes required for summation in the LD simulation. Upon completed both simulations and processing results (volume v temperature plots, and corresponding thermal expansion coefficients) the results were compared. Over the temperature range of 100K - 3000K, there was a clear temperature dependency in the performance of both simulation types. At lower temperatures, the LD simulations exhibited better results relative to the MD, since at low temperatures quantum effects are most dominant - something LD accounts for. At very high temperatures close to the melting point of MgO, LD dynamics breaks down since it cannot take into account anharmonic effects at high temperatures. At higher temperatures, MD doesnt not break down, since it can account for the anharmonic effects, it can allow the ions within the cell to transnationally migrate from their posistion - "effectively break bonds", something which doesnt happen within the Quasi-Harmonic LD simulation. Unfortunately peer reviewed literature across the entire range is neccesary to provide a more useful inside to how well both simulation methods perform. It is important to not that some deviation from literature for both simulation is expected due to the CPU time/demand constraints we have. For MD a much larger grid size could have me used, whilst for LD an ever denser k space grid. Further error can also be introduced within the experiment - which depends on the mathematical functions used to model the various volume v temperature plots, these functions were differentiated directly to obtain thermal expansion coefficients. The experiment also made use of a very simple Buckingham potential to model the interaction between ions, another potential improvement would be to use a more sophisticated potential that also incorporated the the covalent character of the crystal (polarising strength/polarisability of cation/anion considered). Finding a balance between computational demand and accuracy is very important when undertaking computational analysis - this is something that must also be considered if using a more sophisticated potential.
References
1. H. J. Monkhorst, J. D. Pack, Phys. Rev. B:Condens. Matter. , 1976, 13, 5188
2. O. L. Anderson, K. Zou, J. Phys. Chem. Ref. Data, 1990, 19, 69
3. D. Fincham, W. C. Mackrodt, P. J. Mitchell, J. Phys.: Condens. Matter. , 1994, 6, 393-404
4. C. Ronchi, M. Sheindlin, J. Appl. Phys. , 2001, 90, 3325
