Rep:Mod:sp mod3

3rd Year Computational Lab: Module 2 - The Transition State

The Cope Rearrangement

This part of the experiment involves investigating the transition state of the Cope rearrangement for 1,5-hexadiene. By solving the Schrödinger equation numerically, it is possible to locate transition structures based on the local shape of a potential energy surface. This is not possible using Molecular Mechanics and force fields, as in previous modules, as it nvolves bonds being made and broken, as well as changes in bond type and electron density .

The Cope rearrangement is an example of a [3,3]-sigmatropic shift. This pericyclic reaction proceeds via a concerted cyclic transition state. It is a six electron system and proceeds under thermal activstion.

Cope rearrangement mechanism

Optimizing Reactants and Products

1,5-hexadiene was drawn in Gaussview, and the four central Carbon atoms were arranged into the anti conformation using the Dihedral Angle Modifier to set the dihedral angle to -180°. The molecule was then optimized to a minimum using the Hartree-Fock method with the 3-21G basis set. The point group was found by opening the.chk file, accessing Edit->Symmetrize.

1,5-hexadiene in anti conformation

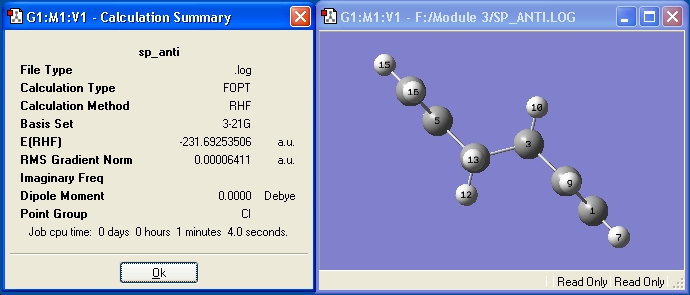
The point group is C_i and the energy (in Hartree) is -231.69253506. The point group and energy value given in Appendix 1, -231.69254, confirm that conformer anti-2 has been optimised.

Next 1,5-hexadiene was drawn with the four central carbon atoms adopting a gauche linkage, the dihedral angle set to 60°, and then optimized to a minimum using the Hartree-Fock method with the 3-21G basis set. Since the gauche configuration is more sterically strained (due to repulsion between the large, diffuse electron clouds of the alkyl groups) it is expected to be higher in energy than the anti-conformer (where the alkyl groups are as far away as possible from each other).

1,5-hexadiene in gauche conformation

The point group is C1 and the energy (in Hartree) is -231.69166701. The point group and energy value given in Appendix 1; -231.69167, confirm that conformer gauche-2 has been optimised. As expected the gauche conformer is higher in energy than the anti conformer (due to the reasons provided above) by 0.00086805 Hartree.

The lowest energy conformer of 1,5-hexadiene is expected to have anti linkage. However, the information in Appendix 1 states that the lowest energy conformer is the gauche-3 conformer. This lead me to think that the gauche conformer may be stabilised by the gauche effect. It is possible that there is donation from the C-H σ orbital into either the C=C π* orbital, or the vacant p orbital orbital on the sp² hybridised carbon atom. However, if that were the case we would expect the gauche conformers to be lower in energy generally, whereas overall the anti conformers are lower i energy. This could be because of the specific arrangement of the allyl group in each individual conformer.

Now the anti-2 conformer of 1,5-hexadiene is optimized using DFT/B3LYP method with a 6-31G* (6-31G(d)). This is a more accurate basis set and method, so we would expect the optimization to produce a lower energy.

1,5-hexadiene in anti-2 conformation, optimized at the B3LYP/6-31G* level

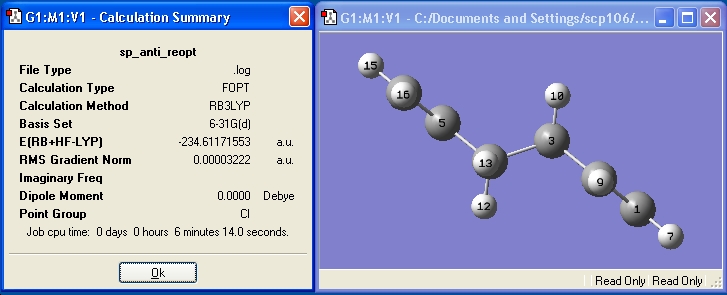
The images of both optimised conformers have been orientated the same way to show how similar the geometries are. The difference in energies between the products optimized using two different methods/basis sets is 2.9198047 Hartree. This is quite a significant change in energy, c.f. energy difference between anti/gauche conformers.

Comparison of anti-2 conformer at the HF/3-21G(left) and B3LYP/6-21G(d)(right)

This side by side comparison of both levels of optimization shows how much the geometry has changed going from the less accurate HF/3-21G level to the more accurate B3LYP/6-21G(d) level. There were slight changes in both the C=C and C-C bond lengths, although these were in the order of 0.0001 Angstrom, and were not thought to affect the geometry of the structure very much. However, there was a large (~4 degree) in the dihedral bond angle (shown above). This is quite a significant change to the overal geometry of the structure.

The results of a frequency calculation carried out at the B3LYP/6-21G(d) level are displayed below.

IR Spectra of anti-2 conformer of 1,5-hexadiene

Thermochemistry of anti-2 conformer of 1,5-hexadiene

The above energies are displayed in Hartree.

Now the Thermochemistry of the anti-2 conformer can be calculated at Absolute Zero (0K). We would expect The 'sum of electronic and zero-point energy' to be the only contribution to the overall energy of the molecule. This is because all the other energetic contribution have a thermal contribution, which would not be present at 0K.

Starting with the optimised molecule, a frequency calculation will be run at the DFT/B3LYP 6-31G(d) level. The intruction 'Freq=ReadIsotope' is added to the input file, and the isototpe mass are changed as intructued in the Advanced Gaussview Tutorial. The temperature was set to 000.0K and pressure to 1.0 atm.

However, after running the calculation the achieved results were not those expected. Upon examining the .log output file, it can be seen that Gaussview has calculated teh freque ncy with the temperature = 298.15 K, and with less accurate masses, hence the energies are different to those quoted above.

Thermochemistry at 298.15K with simplified masses

To rectify this, the calculation was run again, but this time the temerpature was set to 0.00001 K. I suspect that Guassian does not recongnise Absolute Zero as a defined/calculateable temperature, so this problem was solved by setting the temperature to slightly above Absolute Zero. This gave the expected result:

Thermochemistry at 0.00001 K with simplified masses

It is clear that the thermal contributions amount to nothing, as the energy is entirely composed of the electronic contribution and the zero point energy.

Optimizing Transition States

This experiment investigates the chair and boat transition states of the Cope Rearrangement. Three different techniques of optimizing the Transition State will be used; computing force constants at the beginning of the calculation, the redundant coordinate editor and the Intrinsic Reaction Coordinate (IRC) method.

Computing Force Constants at the Beginning of the Calculation

In order for this method to work, a suitable guess of the transition structure first needs to be constructed. This is done by drawing a CH₂CHCH₂ fragment in Gaussview, and optimizing it at the HF/3-21G level. The optimized fragment is then pasted back into the molecule window and the two fragments are arranged into the chair conformer. The terminal ends are set to 2.2 Å apart using the Bond Length Identifier. The fragments are then subjected to a frequency/optimization to a Transition State (TS Berny) calculation, with the Force Constant set to calculate 'Once' and additional instructions Opt=NoEigen.

Optimised chair TS achieved by calculating the Force Constants Once

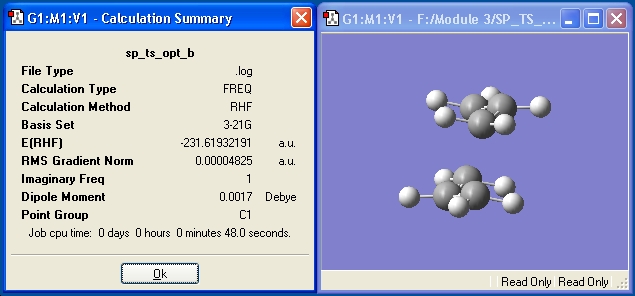
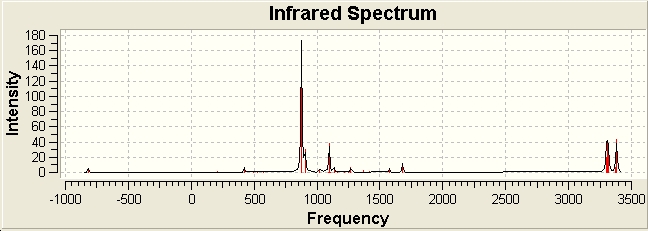
The frequency calculation returns an imaginary frequency at -817.831 cm^-1. The IR spectra is displayed below, along with the imaginary vibration, which corresponds to the Cope Rearrangement.

IR Spectra for Chair TS

Imaginary vibration

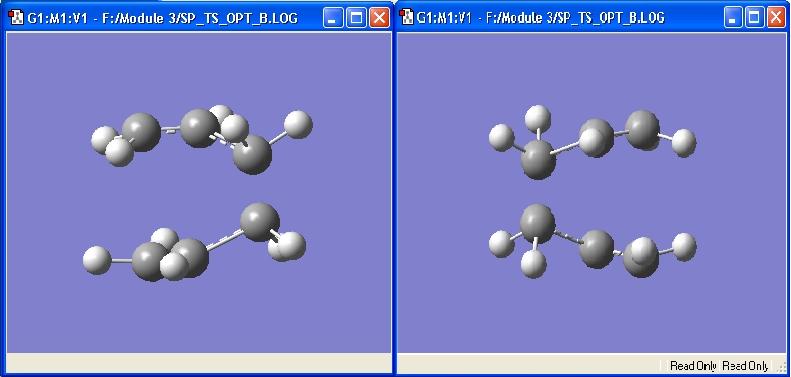
Using the Redundant Coordinate Editor

This method works by first 'freezing' the coordinates of the terminal carbons, i.e. the site where bonds will form. This is done by using the Redundant Coordinate Editor feature of Gaussview, as instructed in the tutorial. This feature is also used to set the bond length to 2.2Å. An optimzation to a minimum, at the HF/3-21G level is carried out. The optimized molecule is then opened in Gaussview, and the previously frozen coordinates are now set to 'bond/derivative'. The molecule is now optimized to a Transition State (TS Berny) and Force Constants not calculated. The optimized product is displayed below

Optimzed product using frozen coordinate method

The C-C bond length of the bond forming is 2.02066 Å, whereas the bond length of the bond breaking is 1.38922 Å. The bond angle of the allyl fragment is 12.0.502°. The geometry of the structure is very similar to the one calculated above (Force Constants Once method). The respective bond lengths of the product calculated using the Force Constants Once methods are 1.97345Å/1.38847Å, with a bond angle of 124.303°. This shows that the force constants once method is a reasonable method where the TS is well known, and can be accurately guessed. However, if it is not possible to accurately guess the TS, the frozen coordinate method is more reliable.

QST2 Method

This method works by manually inputting the reactant and product, and allowing Gaussian to calculate the transition staes. Both molecules were constructed as explained in the tutorial. Initially I had a problem running this calculation, but on closer inspection I realised that while the Carbon atoms were number correctly, the Hydrogen atoms were not. I manually had to change the numbering of the Hydrogen atoms, after which the calculation ran without error. The correctly numbered molecules are shown below.

Starting and Final product in the Gaussian Input File

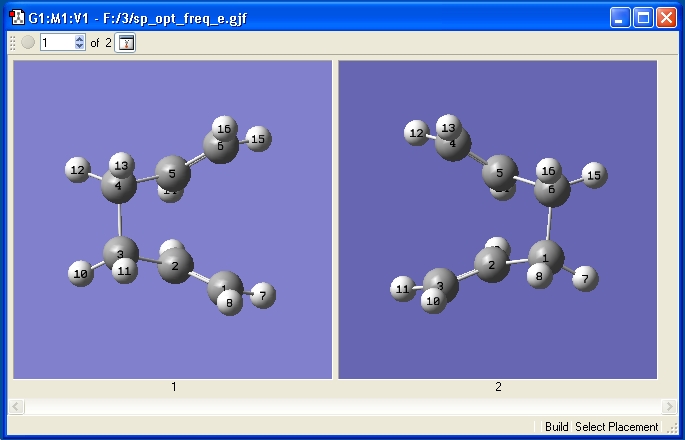
At this stage a Optimization+Frequency Calculation was run. This time the optimization was to a TS (QST2) at the HF/3-21G level.

QST2 optimized Boat TS

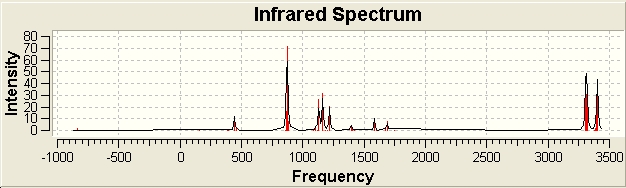
The IR sepctra, and animated imaginary frequency at 840.241 cm^-1, are displayed below.

IR Spectra of Boat TS

Imaginary Vibration of Boat TS

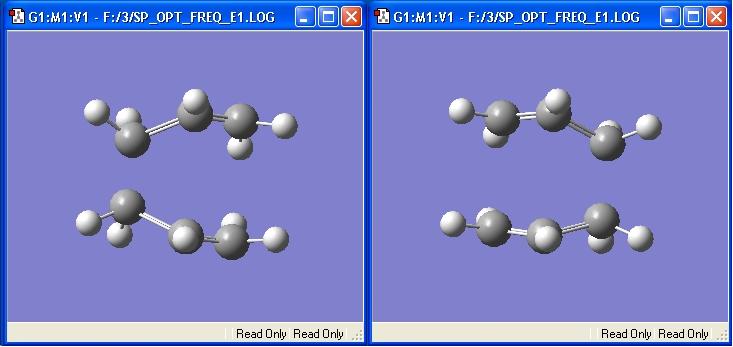
The imaginary vibration corresponds to the bond formation.

Intrinsic Reaction Coordinate (IRC) Method

After the IRC had been run, it was still not optimised after 50 steps, therefore an optimization was run to a minimum, at the HF/3-21G level. The structure generated was 1,5-hexadiene, and was obviosuly not correct, so further claulction were run, and the information displayed in the below table. Additionally, by looking at the RMS gradient, it is not close enough to zero to suggest the lowest energy product has been optimised.

Different IRC methods for chair TS

IRC Method	i)Force Constant=Once, N=50, follwoed by optimization to a minimum	ii)Force Constant=Once, N=100,	iii)Force Constant=Always, N=50
IRC Diagrams
Energy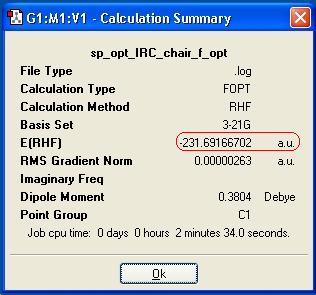

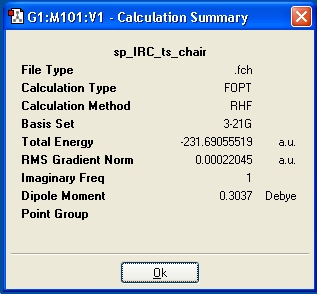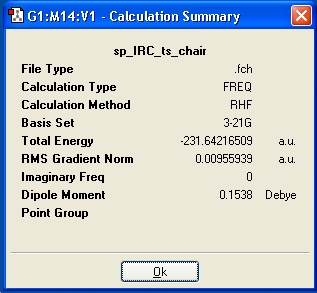Comparison of Theroy Levels

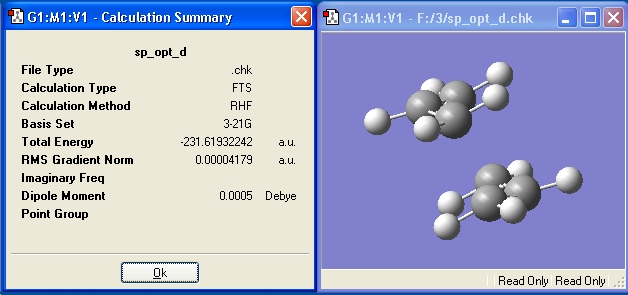
Both the chair and boat TS were optimized at the B3LYP/6-31G(d) level, and are compared to their HF/3-21G counterpart in the table below.

Comparison of energy and theory levels

	Chair at the HF/3-21G Level	Boat at the HF/3-21G Level	Chair at the B3LYP/6-21G(d) Level	Boat at the B3LYP/6-21G(d) Level
Energy (Hartree)	-231.61932242	-231.60280114	-234.55690364	-234.54309251

Although the geometries of the TS optimized by the different theory levels are very similar, the energy values vary by a considerbale amount. In both case the chair conformation is more stable (lower in energy).

At 0K the activation energies for the chair and boat TS are calculated to be 34.06 and 41.96 kcal mol^-1 respectively. This compares very well with the provided litertaure values of 33.5 ± 0.5 kcal mol^-1 and 44.7 ± 2.0 kcal mol^-1 for the chaire and boat respectively.

The chair conformation falls well within the range expressed whereas the boat is slightly oustide. Both sets of data clearly confirm that the reaction proceeds via the chair conformation, as it is substationally lower in energy.

The Diels-Alder Cycloaddition

Cisbutadiene and Ethene

This part of the lab invesitgates the MOs of the following Diels-Alder Reaction

Dials-Alder Reaction

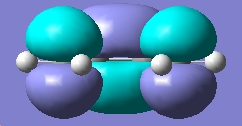
First we will examine the MOs of butadiene. The MOs were plot using AM1 semi-empircal method. The plane is assumed to the vertical plane, as displayed in this diagram, taken from the intructions wiki page.

Butadiene MOs

LUMO			Symmetric wrt plane
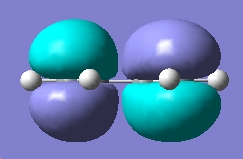
HOMO		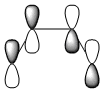	Anti-symmetric wrt plane

Now we can examine the dienophile; ethene. The MOs were plot using AM1 semi-empirical method.

Ethene MOs

LUMO		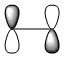	Anti-symmetric wrt plane
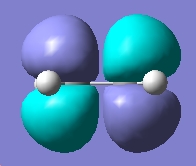
HOMO			Symmetric wrt plane

Transition State

Next the Transition State was constructed as advised, and the MOs were visualize using AM1 smei-empirical method. The distance between the terminal Carbon atoms was set to 2.2 Å, as per the previous experiment. This way then subjected to a opt+freq calculation optimizing to a TS Berny, Force Constants calculated 'Once' and instructions opt=noeigen added at the AM1 semi-empirical level.

Butadiene+Ethene TS MOs

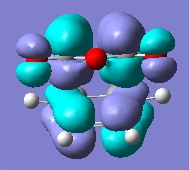
LUMO		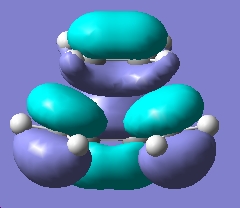Symmetric wrt plane
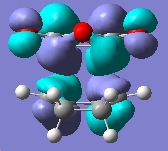
HOMO		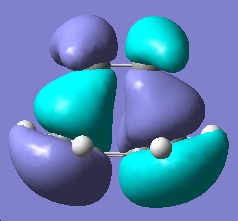Anti-symmetric wrt plane

The following IR spectra was obtained. There is an imaginary peak at -955.702 cm^-1, with the first real peak occuring at 146.919 cm^-1. Whereas the imaginary peak corresponds to a vibration which simulates bond formation, the first real frequency peak corresponds to the ethene group 'rocking' from side to side.

IR Spectra of TS showing imaginary vibration

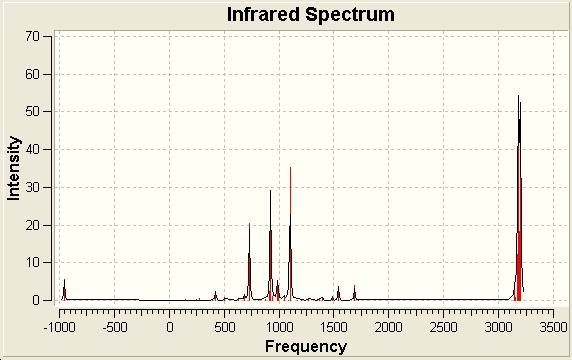
The existance of an imaginary vibration confirms this is a Transition State. If it is animated, it shows the bond forming process:

Animation of imaginary vibration

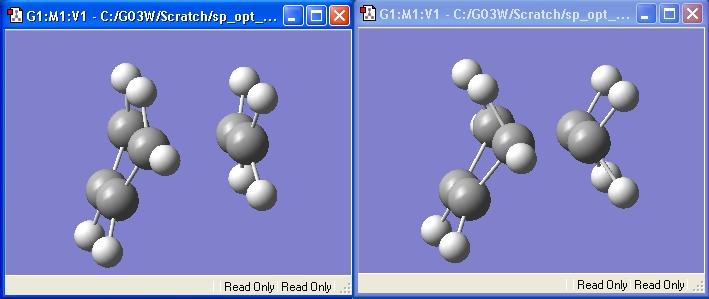
The two bonds form in a synchronous fashion.

The geomtery of the TS is shown in the diagram below.

Geomtery of TS

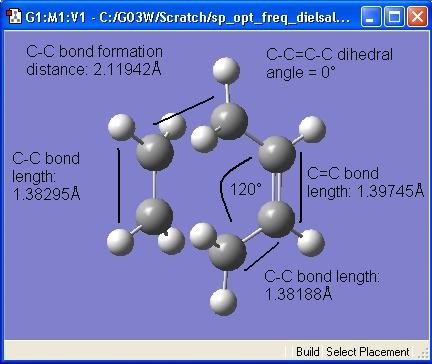
Literature values for C-C and C=C bond lengths were found to be 1.54Å and 1.33Å . The calculated C-C bonds are a similar to the literature values, whereas the C=C bond is quite different to its literature. It may have something to do with the fact that in the TS the bonds are breaking/forming, and this will be reflected in Gaussian having 'average' bond lengths, whereas the literature bond lengths were measured in stable species.

The calculated C--C (bond forming) distance is 2.119 Å, which corresponds well with the literature value of 2.285Å

The van der Waals radius for the Carbon atiom is reported to be 1.7Å .

The TS is made up of the HOMO from cis-butadiene and LUMO from the ethene, and the TS is antarafacial. The reaction is allowed according to the 'selection rules' of pericyclic reaction. A 4n+2 electron system may proceed via thermal activation through an antarafacial TS.

Exo/Endo forms of Maleic Anhydride

The endo/exo transition states were constructed by drawing a 'guess' strcuture, and optimizing to a TS Berny with force constants calculated once, keyworkds opt=noeigen, at the semi-empirical AM1 level.

Endo and Exo TS

	Endo	Exo
3D Molecule	Mol_1	Mol_1
LUMO
HOMO
Imaginary Frequency (cm-1)	-805.755	-811.523
Animated Imaginary Vibration
Mean Bond forming distance (Å)	2.16236	2.17039
Energy (in Hartree)	-0.05159430	-0.05050322

The data above shows that the endo transition state is lower in energy than its exo counterpart, meaning that the endo form is the kinetically favoured product. The energy difference between the endo and exo form is 0.6842 kcal mol^-1. Both TS exhibit imaginary frequencies, confirming that they are indeed transition states.

By looking at the 3D molecules, we can see that in the exo form, the carbon atoms in the cyclohexene ring which lie below the maleic anhydride are sp³ hybridised, whereas in the endo form they are sp² hybridised. The difference is due to the position of the C=C bond. The sp² carbons are planar, and as a result experience less steric interaction with the maleic anhydride. The sp³ carbons are not planar, and experience more steric interaction with the maleic anhydride ring.

Further evidence which supports the fact that the endo is favour is the average bond forming lengths. The terminal carbons where bonding would take place are closer together in the endo TS than the exo TS.

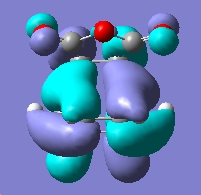
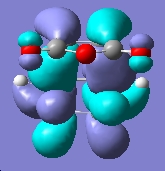
By examining the orbital interactions it is clear that in the transition state for the endo dimer favourable secondary orbital interactions are present. Such interactions are not present in the transition state of the exo dimer. The dashed line represents the secondary orbital interaction, whereas the wide hashed line represents the bonds forming.

Example of Secondary Orbital Interaction

Exo Transition State	Endo Transition State