Rep:Mod:sp mod2

3rd Year Computational Lab: Module 2 - Bonding

Day 1

BCl₃

The BCl₃ optimisation described in the introduction was recreated for this report. The optimised molecule and the calculation summary, which contains all the requested information, are displayed below.

BCl₃ molecule and calculation summary

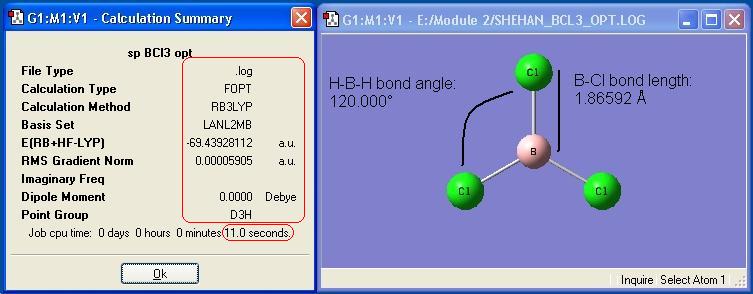
Small Molecule

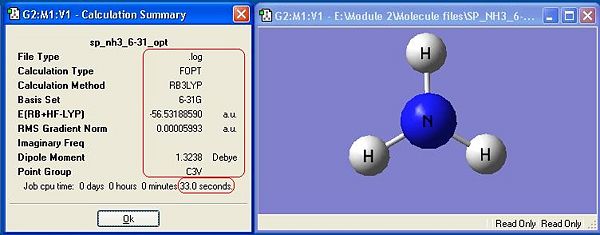
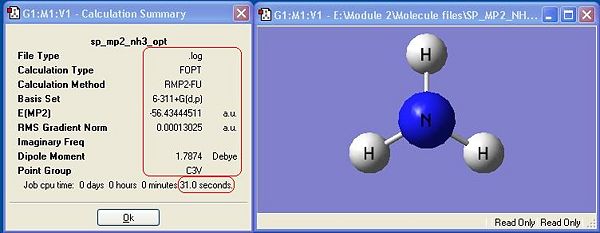
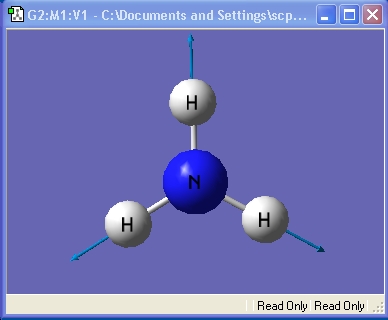
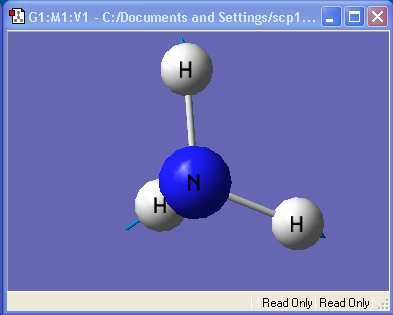
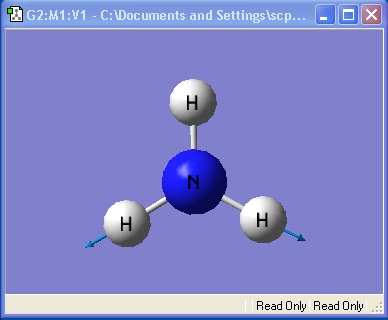
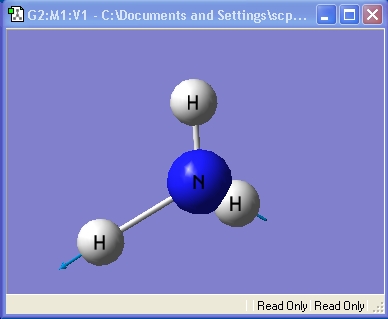
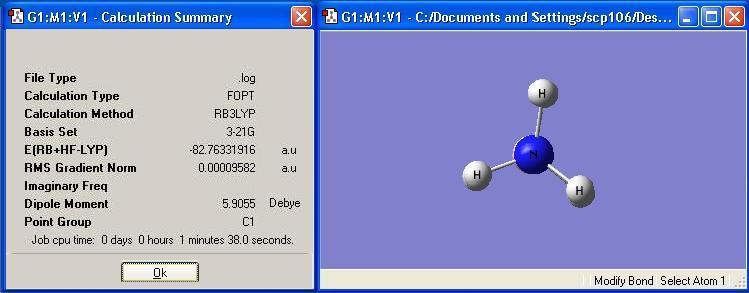
Ammonia, NH₃,was chosen as the small molecule to optimise. The optimised molecule and the calculation summary, which contains all the requested information, are displayed below.

Ammonia molecule and calculation summary

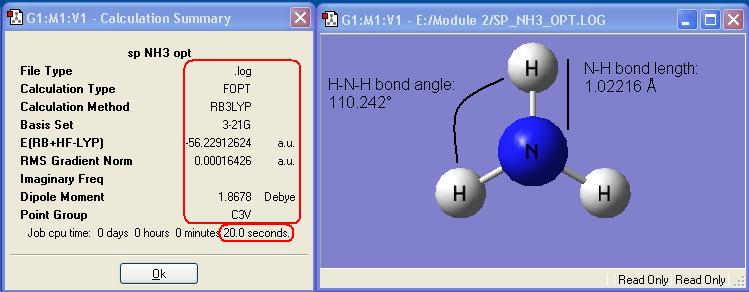
The xyz Cartesian co-ordinates were available in the .log file:

Published here:DOI:10042/to-1106

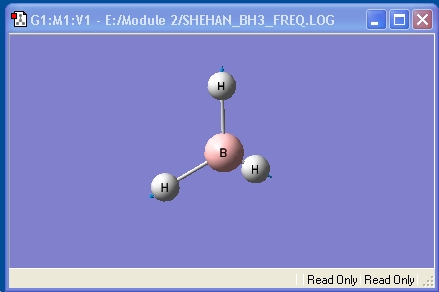
BH₃

The BH₃ optimisation described in the introduction was recreated for this report. The optimised molecule and the calculation summary, which contains all the requested information, are displayed below.

BH₃ molecule and calculation summary

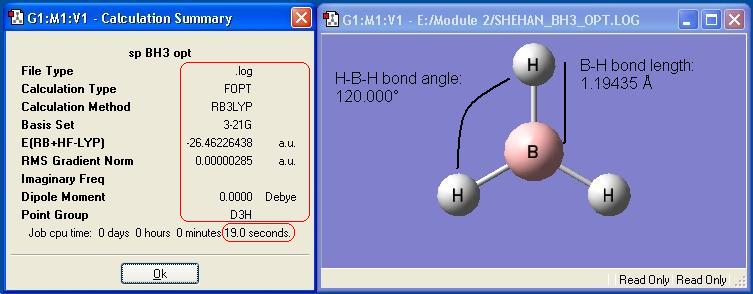
Vibrational Analysis of BH₃

The vibrational analysis was carried out as instructed, and the information acquired is displayed in the table below:

Table showing vibrations of D_3h BH₃ molecule

Vibration Number	Image	Description	Frequency (cm-1)	Intensity	Symmetry
1		All 3 H atoms simultaneously move above and below the plane of the molecule	1145.71	92.6991	A1"
2		2 H atoms 'scissor'	1204.66	12.3789	E'
3		The 'bottom' H atom moves side to side, while the other 2 H atoms rock	1204.66	12.3814	E'
4		All 3 B-H bonds simultaneously/symmetrically stretch	2592.79	0	A2'
5		2 B-H bonds stretch asymmetrically, 1 remains still	2731.31	103.837	E'
6		2 B-H bonds stretch symmetrically, 1 B-H bond asymmetrically	2731.31	103.83	E'

IR Spectrum of BH₃

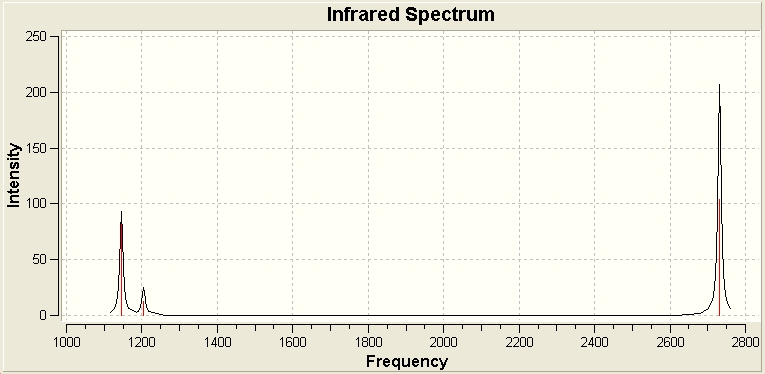
From looking at the table there are 6 defined vibrations. However, of these 6, there are two pairs of vibrations which have identical frequencies. This reduces the expected number of peaks from 6 to 4. Also from the table, we can see that vibration 4 has an intensity of 0. This vibration therefore does not show up on the spectra. The reason that this particular vibration is not observed is that there is no change in dipole. This leaves the 3 vibrations observed in the spectra.

Molecular Orbital Analysis of BH₃

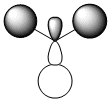
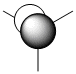
The quantitative Molecular Orbitals are displayed with their respective qualitative Molecular Orbitals in the table below

Molecular Orbitals BH₃

Molecular Orbital	1	2	3	4	5
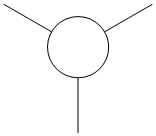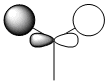Qualitative Orbital	Orbital 1	Orbital 2	Orbital 3	Orbital 4	Orbital 5
Quantitative Orbital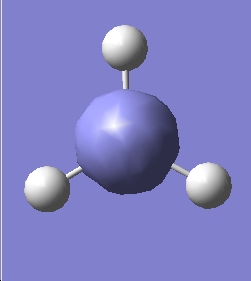
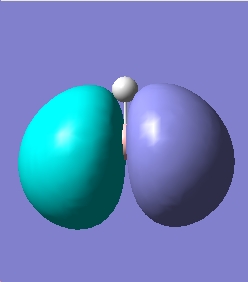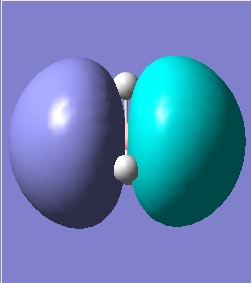Orbital Energy	-6.730	-0.517	-0.356	-0.356	-0.074

Talk about energy

Using the available literature , the following MO diagram was produced in ChemDraw:

MO Diagram

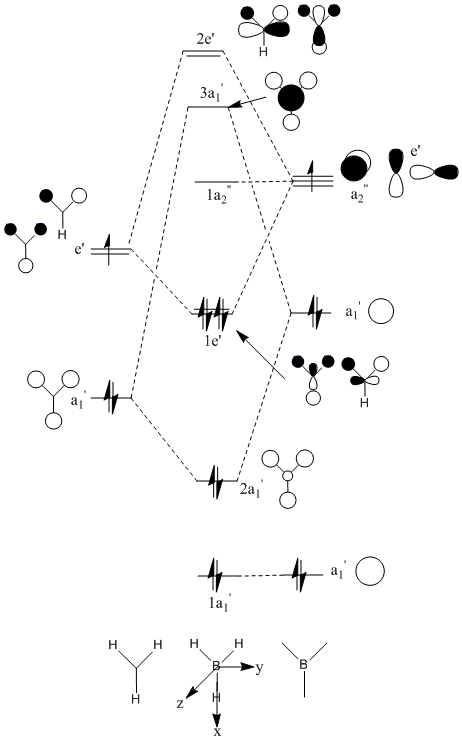
From looking at both the qualitative and quantitative MOs it is clear that they correlate very well, both in shape and electron density. Although when comparing the two sets of Mos, we must bear in mind that the qualitative MOs consist of linearly combined Atomic Orbitals. Where we see multiple AOs in a qualitative MO, they construcitvely (in pahse) overlap to form single lobes, we expect (and observe) a single 'phase' lobe/orbital in the quantitative MO. Where we see destructively (out of phase) overlap, we expect (and observe) nodes in the quantitative MO.

The fact that the qualitatitive and quantitative MOs correlate so well (at least for low energy MOs in a simple inorgnic molecule) indicates that qualitative MO theory is a good model, as it can quickly and accurately predict MOs without the need for a computer/calculations. It would be worth investigating whether MO theory holds up well ifapplied to more complex molecules, such metal complexes, aromatic systems, multicentre multielectron bonds (e.g. B₂H₆). cf VESPR to MO.

Day 2

Isomers of Mo(CO)₄L₂

The cis and trans isomer were initially optimised using the B3LYP method with a LANL2MB basis set, with the convergence criteria 'opt=loose'. After this, it was further optimised using the LANL2DZ basis set, with the electronic convergence 'int=ultrafine scf=conver=9'. Both optimisation were done using SCAN. Once the fully optimised geometries were returned from SCAN, vibrational frequency calculations were run on each isomer. The obtained results, as well as the fully optimised 3D molecule for each isomer are displayed below. To calculate the energy of each isomer in kJ mol^-1, it was converted from Hartrees to Joules, then scaled up to a mole:

E_J=(E_H x 4.359 744 17 x 10^-18 x 6.0221415 × 10²³)/1000

where E_J is energy in Joules and E_H is energy in Hartree

cis and trans isomers of Mo(CO)4PMe₃

Isomer	Fully optimised cis-Mo(CO)4PMe3	Fully optimised trans-Mo(CO)4PMe3
3d Molecule	Mol_1	Mol_1
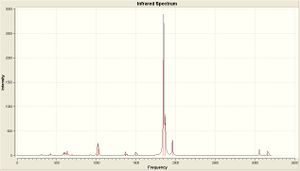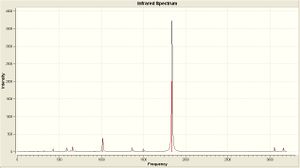IR Spectra	cis isomer	trans isomer
Calculated Frequency (cm-1)	1848.43/1850.53/1869.89/1960.3	1839.5/1839.29
Literature Frequency (cm-1)	1882/1903/1917/2022	1901
Energy (kJ mol-1)	-2030457.024	-2030449.336

From the information above we can conclude that the trans isomer is more stable. This would be expected due to the reduction in steric interaction of the PR₃ groups when in the trans isomer. The energy difference is calculated as 7.688 kJ mol^-1.

As is clear from the IR there is only one dominant peak in each spectra (at about 1900 cm^-1) which corresponds to the C=O stretch. It is also clear that there are numerous peaks for this range in the cis isomer spectra, where the trans spectra has a well defined peak. This peaks have been defined above in the table, as well as the corresponding literature value (or as close as I have been able to tell). The vibrational frequency for the trans isomer compares favourably, and is within 3%. The cis isomer compares equally favourably, with all the calculated frequencies within 3%.

cis and trans isomers of Mo(CO)4PMe₃

Isomer	Mo-P Calculated Bond Length (Å)	Mo-P Literature Bond Length (Å)	Mo-C Calculated Bond Length (Å)	Mo-C Literature Bond Length (Å)	P-Mo-P Calculated Bond Angle	P-Mo-P Literature Bond Angle
cis isomer	2.652/2.648	2.522	2.032/1.981/1.983/2.031	2.042/1.966/1.975/2.022	95.31°	97.54°
trans isomer	2.572	2.500	2.028/2.029	2.005/2.016	179.83°	180°

In both the literature reports the complex was of the form Mo(CO)₄(PR₃)₂. For the cis isomer R=Me (the exact same molecule, so we can expect better correlation between calculated and experimental values) but for the trans isomer R=Ph, so we may expect slightly more disparity between results. Unexpectdely it is the trans isomer that correlates better with its experimental values, the P-Mo-P bond angle is very close to the experimentally measured angle. All the bond lengths are within 3% of the experimentally measured ones.

In the cis isomer the differences in bond lengths and angle are greater; 5% and 2.4% respectively. In both isomers the best match is between the Mo-C bonds (difference ~1%) and the Mo-P bonds show the greater difference (3-5%). Since the d orbitals are not used in he calculations the bonds with the lowest d character (Mo-C)are the best predicted, whereas the Mo-P bond which has a lot of d character is (relatively) poorly predicted.

However, both isomers are within a reasonble degree of accuracy considering that a medium level basis set/method was used, and that the d orbitals were not included in the calculations. Had the advance method/basis set been used (which included the d orbitals), I would expect the bond lengths/angle to be even closer to the literature value.

It may be possible to alter the relative ordering of the cis/trans isomers by adjusting the ligands steric and electronic properties. By adding large steric groups, or EWG/EDG it would be possible to alter the steric and electronic factors repectively. There is the possibility that such interactions can activate or improve a metal's ability to act as a catalyst. Catalysts are often improved by making slight changes to secondary groups on the ligands themselves, while leaving the metal center/bonding ligand intact. Additionally, where regiospecific catalysts are required, groups on ligands can be selected as to favour a specific isomer.

Day 3

Quantum Nature of Ammonia

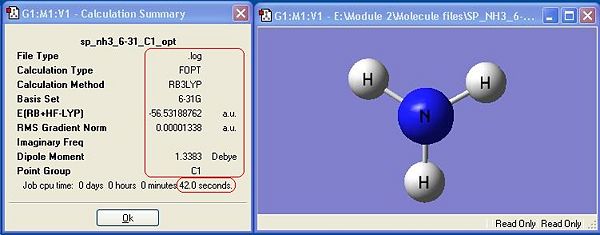
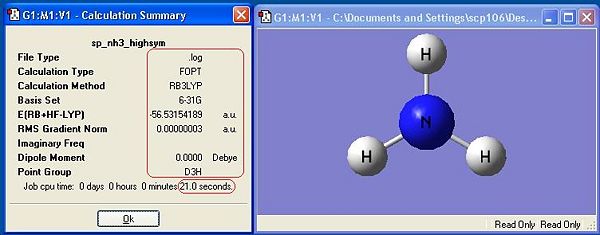
Symmetry

Comparison of ammonia symmetry

Point Group	Method/Basis Set	Image	Energy (kJ mol-1)	ΔE (kJ mol-1)
C3v	B3LYP/6-31G		-148424.4664	0.9032
C1	B3LYP/6-31G		-148424.4709	0.9077
D3h	B3LYP/6-31G		-148423.5632	N/A
C3v	MP2/6-311+(d,p)		-148168.6356	20.4684
D3h	MP2/6-311+(d,p)		-148148.1672	N/A

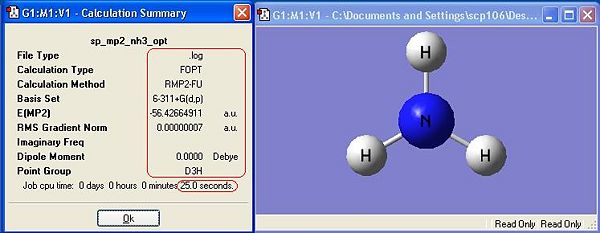
The symmetry has made a difference to the final structure obtained. This is shown by the differences in energy between the first 3 molecules. There is a distinct, albeit very small difference in energy, with C₁ being the lowest, thus most stable symmetry.

The general trend observed is that the higher the symmetry, the quick a molecule is optimised. This is because symmetry must be retained during the calculation, so as the programme optimises the geometry, it has fewer possible optimisation steps because symmetry must be retained. There are statistically fewer different co-ordinations the molecule can be arranged in while remaining symmetrical.

During the calculation symmtery must be retained, and cannot be broken unless specifically specified (the tickable 'ignore symmetry' box in Gaussview). This means that high symmetry structure optimise more quickly.

The lowest energy geometry is C₁, whereas the highest symmetry D_3h is the highest in energy. The difference in energy between these two geometries is 0.9007 kJ mol^-1. The difference in energy between these two geometries is very low, and at room temperature there is sufficient energy to overcome it. This means that Ammonia is constantly switching between the two geometries in an umbrella type motion. From equipartition theory (T=298K):

E= 3/2 kT E(per mol) = 3/2 RT E= 3.716 kJ mol^-1

The calculations for the better basis set/method took on average longer. However, since the laptops can be 'temperamental' the above data isn't the most conclusive evidence of this we are likely to see. However, were slightly larger molecules considered, the better basis set/method calculations would take longer.

The energy difference calculated (20.4684 kJ mol^-1) compares quite well with the experimentally determined energy barrier (24.3 kJ mol^-1). There is a 16% difference between the energies. The energy difference for this basis set is much greater than the energy differenec for the previously used basis set.

Vibration

IR Spectra for C_3v and D_3h point groups of NH₃

Point Group	C3v	D3h
IR Spectra	C3v	D3h

Comparison of C_3v and D_3h point groups for NH₃

C3v Vibrational Mode	C3v Frequency (cm-1)	D3h Vibrational Mode	D3h Frequency (cm-1)
	452.302		***-318.051***
	1680.47		1640.59
	1680.47		1640.59
	3575.43		3635.71
	3775.76		3854.27
	3775.76		3854.27

Computational and Experimental Vibrational Frequency for C_3v point group of NH₃

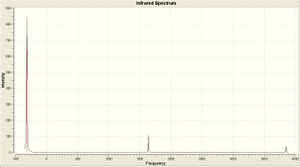Computational Frequency(cm -1)	452.302	1680.47	1680.47	3575.43	3775.76	3775.76
Experimental Frequency(cm -1)	932	1626	1626	3337	3444	3444

The first frequency has a very large difference of ~50%. However, the remaining 5 are within 9% of the literature values.

Mini Project

Fuels of the Future

Staggered BH₃NH₃ was optimised and the calculation summary is displayed below:

Staggered conformation

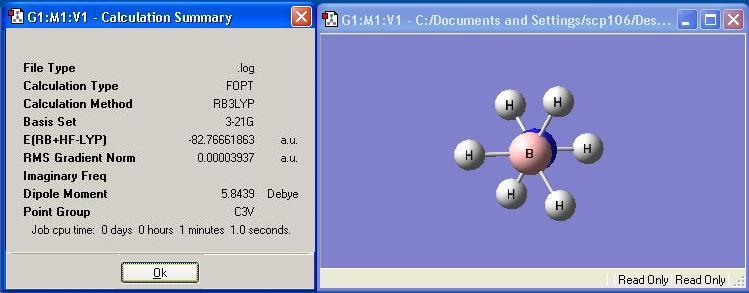
Eclipsed BH₃NH₃ was optimised and the calculation summary is displayed below:

Eclipsed conformation

The staggered conformation is the lowest in energy, thus most stable form. The energy difference between the two conformations is 8.663 kJ mol^-1.

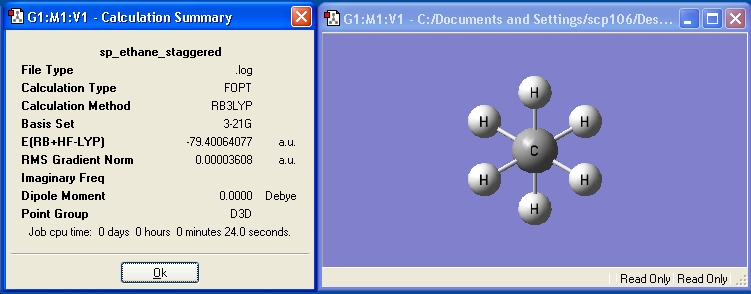
Staggered ethane was optimised and the calculation summary is displayed below:

Staggered conformation

Eclipsed ethane was optimised and the calculation summary is displayed below:

Eclipsed conformation

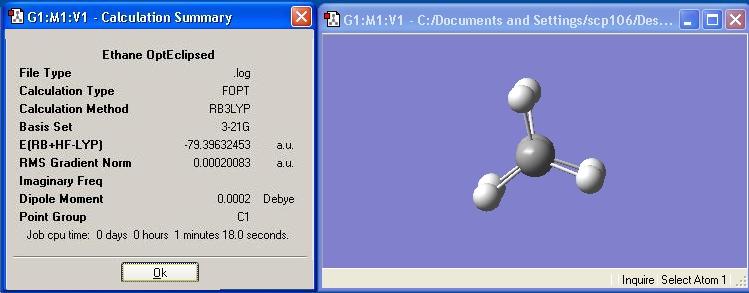
Again the staggered conformation is the lowest in energy, thus most stable form. The energy difference in this case is 11.327 kJ mol^-1. This energy difference is some 30% larger than the respective difference between conformers of ammonia borane.

In ethane we expect the electron density of the C-C bond to be evenly spread, and all the C-H bonds to be equal. However, in ammonia borane the electron density of the N-B bond would be more around the N atom, as Nitrogen is more electronegative. This would also cause the N-H bonds to be shorter than the B-H bonds (0.96Å vs 1.15Å ).

Ammonia borane is lower in energy than both starting product. Additionally, the formation of Hydrogen gas provides an entropic driving force for the reaction.

The large difference in melting points between ethane and ammonia borane is due to the highly polar nature of the molecule. The hydrogen atoms bonded to nitrogen are acidic in character, whereas the hydrogens bonded to boron are basic in nature. Studying the solid structure has indicated "close association of the NH and BH centres".