Rep:Mod:sp mod1

3rd Year Computational Lab: Module 1 - Structure and Spectroscopy

Modelling using Molecular Mechanics

This section of the experiment involves using Molecular Mechanics, specifically the MM2 force field via the ChemBio3D Ultra program, to quickly and easily optimize the geometry of small, simple molecules. This computational technique uses Newtonian mechanics to model molecular systems, whose potential energy can be calculated. By the summation of individual bond properties, several molecular properties can be accurately attained without the need for complicated calculations. The MM2 forcefield was developed by Norman Allinger.

A molecular systems potential energy can be expressed as

where

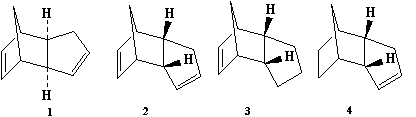
The Hydrogenation of the Cyclopentadiene Dimer

This section investigates the formation and hydrogenation of Cyclopentadiene dimers. Molecular mechanics (MM2) will be used to optimize their geometries and calculate energies. This information will then be used to rationalise the formation of the dimers and will help to determine whether the reactions are thermodynamically or kinetically influenced.

Cyclopentadiene dimers and hydrogenated products

Table showing energies of Cyclopentadiene dimers and their hydrogenated products

Energetic Contribution (kcal mol-1)	Cyclopentadiene Exo Dimer 1	Cyclopentadiene Endo Dimer 2	Hydrogentated Product 3	Hydrogentated Product 4
Stretch	1.2829	1.2520	1.2244	1.0973
Bend	20.5879	20.8751	18.8500	14.5063
Stretch-Bend	-0.8341	-0.8337	-0.7530	-0.5495
Torsion	7.6718	9.5060	12.2374	12.4976
Non-1,4 VDW	-1.4355	-1.5490	-1.5459	-1.0512
1,4 VDW	4.2324	4.3029	5.7556	4.5127
Dipole/Dipole	0.3778	0.4468	0.1631	0.1407
Total energy	31.8832	34.0001	35.9317	31.1539
3D Molecule	Mol_1	Mol_2	Mol_3	Mol_1

Comparison of Compounds 1 & 2

From the above table we can see that dimer 1 is lower in energy, thus more stable, than dimer 2. By analysing the table we can also see where the disparity in energy originates from. The difference in energy between the two dimers is 2.1169 kcal mol^-1, which is almost entirely made up of the differences in torsion energy (1.8342 kcal mol^-1). This indicates that the difference in energy between the two dimers is almost exclusively due to the increased strain in dimer 1. This can best be visualised through the use of Newman Projections of each dimer.

Orbital Interactions

Exo Dimer 1	Endo Dimer 2

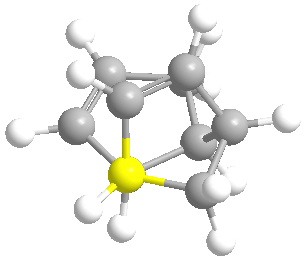In dimer 1, the alkyl groups are antiperiplaner (app) to each other. This greatly reduces steric interaction (electron cloud repulsion) between the two large groups, hence the lower torsion energy. Dimer 2, however, has the alkyl groups in the Gauche conformation, and has more steric interaction than in dimer 1, hence the higher torsion energy. These images help to explain why dimer 1 is lower in energy than dimer 2.

Talk about conjugation

However we know that the dimerisation of Cyclopentadiene exclusively favours dimer 2. Therefore we can conclude that this process is kinetically controlled, as the more stable dimer is not favoured.

Since it is the kinetic product, it is implied that transition state for the endo dimer is lower in energy than the exo dimer. By examining the orbital interactions it is clear that in the transition state for the endo dimer favourable secondary orbital interactions are present. Such interactions are not present in the transition state of the exo dimer. The formation of the endo transition state is irreversible, which explains why the kinetic product is formed exclusively. The dashed line represents the secondary orbital interaction, whereas the wide hashed line represents the bonds forming.

Newman Projections of Dimers 1 & 2

Exo Transition State	Endo Transition State

Comparison of Compounds 3 & 4

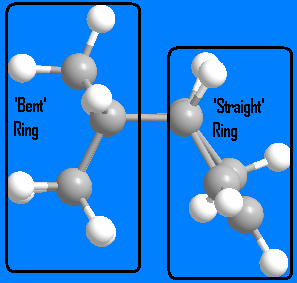
From examining the above table, we can see that dimer 4 is more stable than dimer 3 by 4.7778 kcal mol^-1. Since there are no kinetic influences (hydrogenation of a particular double bond is not mechanistically favoured) the more stable, thermodynamic product is formed. Again we can see that the majority of the difference in energy is caused by the difference in bending energy (4.3437 kcal mol^-1). In dimer 3, the alkene on the 'straight' 5 membered ring is hydrogenated. The introduction of two more sp³ hybridised carbons causes more bending than the planar sp² carbons, hence the higher bending energy. However, in dimer 4, the alkene on the 'bent' 5 member ring is hydrogenated. Since the ring is already bent (because of where the two cyclopentiene rings join), the introduction of sp³ hybridised carbons does not cause as much bending as in dimer 3. Dimer 3 adds bending to a previously straight ring, whereas dimer 4 slightly increases bending in an already bent ring while preserving the 'straight' ring.. This explains the difference in bending energy for each dimer, and ultimately why dimer 4 is more stable than dimer 3.

Ring bending

Dimer 3	Dimer 4

Stereochemistry of Nucleophilic additions to a Pyridinium ring

This section investigates how molecular mechanics can be used to rationalise mechanisms, specifically nucleophilic addition to a Pyrindinium ring.

Reaction Scheme

Mechanism

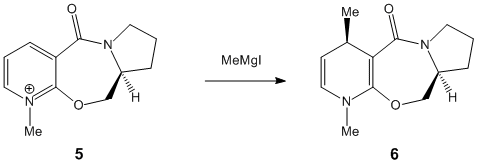
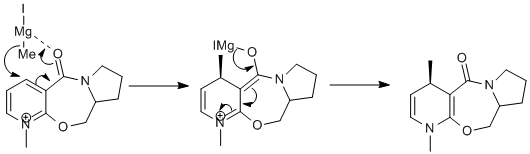
If MeMgI is present the optimization does not work because MM2 does not recognise Magnesium. The following table was composed by first setting the dihedral angle to a predefined one, then minimised. This was done to see what affect the starting angle had on the total energy.

Table showing how starting angle affects total energy

Energetic Contribution (kcal mol-1)	Starting Dihedral Angle of 90o	Starting Angle of 180o	Starting Angle of -90o
Stretch	1.5427	1.5943	1.5383
Bend	6.8049	6.2843	6.6031
Stretch-Bend	0.3347	0.3182	0.3307
Torsion	-6.3165	-5.5464	-6.0919
Non-1,4 VDW	-1.8665	-2.1235	-2.0682
1,4 VDW	17.5994	17.5181	17.6029
Charge/Dipole	2.3642	2.3645	2.3827
Dipole/Dipole	-4.7974	-4.7917	-4.7907
Total energy	15.6654	15.6178	15.5069
Final Dihedral Angle	-39.6289	-47.2354	-41.7563

Dihedral angle

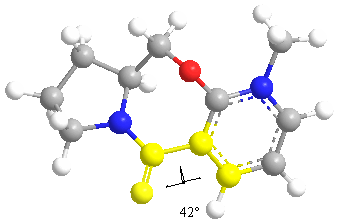
The lowest energy is achieved when the dihedral angle is -41.7563. The Methyl group adds on after the chelation of the carbonyl group. The mechanism proceeds via a cyclic transition state.

Reaction scheme

Mechanism

Table showing how starting anlges relate to energy

Energetic Contribution (kcal mol-1)	Starting Dihedral Angle of 90o	Starting Angle of 180o	Starting Angle of -90o
Stretch	1.5428	1.5959	1.4973
Bend	6.7656	6.2006	5.9541
Stretch-Bend	0.3339	0.3216	0.3224
Torsion	-6.3718	-5.2745	-4.8185
Non-1,4 VDW	-1.7265	-1.7350	-2.3923
1,4 VDW	17.5723	17.5100	17.5150
Charge/Dipole	2.3627	2.3944	2.4340
Dipole/Dipole	-4.7908	-4.7816	-4.7786
Total energy	15.6884	15.6270	15.7334
Final Dihedral Angle	-40.2827	-47.4660	-48.5179

Dihedral Angle

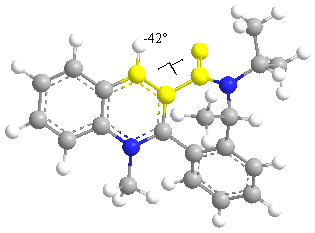
In this reaction the nucleophile attacks the least hindered site. The substituent lies above the plane of the aromatic ring to reduce steric hindrance.

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

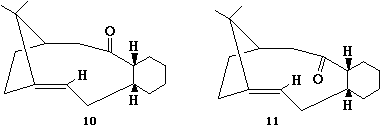
This section investigates the stability of two isomers of key intermediate in the synthesis of Taxol. Molecular mechanics (MM2) will be used to optimize their geometries and calculate energies. This information will then be used to determine the most stable isomer and explain why the alkene reacts slowly. The two isomers are atropisomers; stereoisomers where steric strain is high enough to prohibit rotation about single bonds resulting in separable conformers.

Atropisomers of a Key Intermediate in the Synthesis of Taxol

Intermediates in Taxol Synthesis

Energetic Contribution (kcal mol-1)	Taxol Intermediate 10	Taxol Intermediate 11
Stretch	3.0567	2.6563
Bend	19.0747	13.2610
Stretch-Bend	0.2753	0.3243
Torsion	20.5288	20.0996
Non-1,4 VDW	0.2515	-0.0787
1,4 VDW	14.8623	13.4066
Dipole/Dipole	0.0406	0.2829
Total energy	58.0899	49.9520
3D Molecule	Mol_1	Mol_1

After initially sketching isomer 10 in ChemDraw it was reopened in ChemBio3D and optimized. The initial optimization resulted in a total energy of 121.3422 kcal mol^-1. In this conformation the carbonyl group is roughly perpendicular to the ring. By manually moving this carbonyl group to the 'up' position (same direction at the bridging alkyl group) and adjusting the Cyclohexane into the chair conformation the total energy of 58.0899 kcal mol^-1 was obtained.

After the inital sketch and optimization of isomer 11 an energy of 51.4524 kcal mol^-1 was achieved. Following manual adjustments the total energy 49.9520 kcal mol^-1 was obtained for the carbonyl 'down' isomer (carbonyl anti/opposite to the alkyl bridging group).

The difference in energy between isomers 10 and 11 (8.1379 kcal mol^-1) is largely composed of the differences in bending energy (5.8137 kcal mol^-1). With the isomer in the 'up' position there is steric interaction with the bridging alkyl group, where if it is 'down' there is less steric interaction.

The alkene is both isomers react slowly due to a combination of factors. Firstly both rings are very hindered, which would prohibit the hydrogenation of the double bond. Secondly, and perhaps more importantly, due to the transannular strain introduced into the ring system as two carbon go from sp² hybridised to sp³ hybridised. As the two carbons adopt a tetrahedral geometry, additional strain is caused as the bond angle goes from 120^o to 109^o. When the alkene is present, the carbons adopt a trigonal planar geometry which does not cause as much strain as the tetrahedral geometry. As the trigonal planar geometry occupies more space, the ring is less crowded than when it is tetrahedral.

This can be shown by hydrogenating the alkene, and examining the resulting molecule:

Hydrogenation of Taxol Intermediates

Hydrogenated Taxol Intermediate 10	Hydrogenated Taxol Intermediate 11
71.6308 kcal mol-1	71.5508 kcal mol-1
Mol_1	Mol_1

Both 10 and 11 greatly increase in energy when hydrogenated (13.5409 and 21.5988 kcal mol^-1). Since the products of the hydrogenation are much higher in energy than the reactants the reaction is thermodynamically unfavoured, and the alkene reacts slowly.

Room Temperature Hydrolysis of a Peptide

This section involves the use of Molecular Mechanics to calculate the energy of four isomers and rationalise the kinetic behaviour of peptide hydrolysis.

Peptide hydrolysis

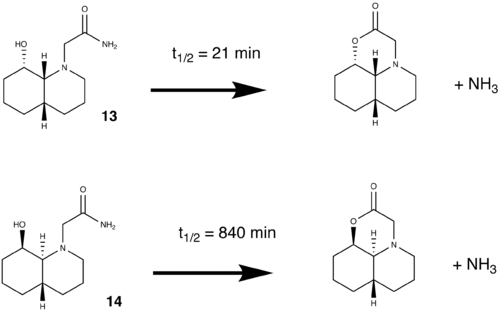
All the molecules were sketched in ChemBio3D using the chair-chair conformation. From this starting point, the molecules are manually adjusted into the required conformations and minimized. From this point the molecules needs further manual adjusting to minimize its energy. The lowest achieved energy is displayed in the table below

Table showing energies of peptide isomers

Energetic Contribution (kcal mol-1)	13 - OH Equatorial/N-substituent Equatorial (Eq/Eq)	13 - OH Equatorial/N-substituent Axial(Eq/Ax)	14 - OH Axial/N-substituent Equatorial (Ax/Eq)	14 - OH Axial/N-substituent Axial(Ax/Ax)
Stretch	1.5133	1.3804	1.4764	1.6971
Bend	7.7689	3.9971	4.2767	5.5274
Stretch-Bend	0.6642	0.5181	0.5687	0.6097
Torsion	8.8809	9.3587	7.1705	8.7294
Non-1,4 VDW	-5.6902	-5.1512	-5.2492	-5.1217
1,4 VDW	9.2753	9.4266	9.4146	9.4997
Dipole/Dipole	-7.4243	-3.3129	-3.5977	-6.8234
Total energy	14.9881	16.2169	14.0600	14.1183
3D Molecule	Mol_1	Mol_2	Mol_3	Mol_1

For both 13 and 14, the most stable isomer are when the N substituent is equatorial, as this reduces 1,3-Diaxial compression.

The half life of the peptide depends on two factors; intramolecular Hydrogen bonding and the angle of approach (Burgi-Dunitz angle). Hydrogen bonding stabilizes the molecule, making the hydrolysis thermodynamically unfavoured. The hydrolysis can only take place is the OH and C=O are is a specific arrangement; Burgi-Dunitz angle.

Of all 4 isomers, only one (eq/eq) has the correct configuration in accordance with the Burgi-Dunitz angle (107^o). The lone pair on the oxygen (of the hydroxyl group) is in the correct position with respect to the C=O π*, which facilitates the hydrolysis. The reason why molecule 13 has a much lower half life is because only an isomer of 13 can undergo the reaction easily. Since the eq/eq isomer is lower in energy than eq/ax (by 1.2288 kcal mol^-1) it is the more stable, favoured isomer. Additionally at room temperature (298K) there is not sufficient energy for it to adopt the eq/ax configuration.

From equipartition theory:

E= 3/2 kT E(per mol) = 3/2 RT E= 3.716 kJ mol^-1 = 0.888 kcal mol^-1 (1 kcal = 4.184 kJ)

Since the energy difference between the two isomer is greater than the kinetic energy supplid by room temp, the eq/eq is the most favoured isomer.

In molecule 14, strong intramolecular hydrogen bonding between the amide and hydroxl groups (and carbonyl-hydroxyl) prohibits free rotation making the molecule very stable against peptide hydrolysis.

Modelling Using Semi-empirical Molecular Orbital Theory

In the previous experiments Molecular Mechanics has been used to successfully optimize and calculate energy of simple organic molecules. While the technique is quick and non-intensive (with respect to processing power) it does have limitations. For example, the secondary orbital interactions in the formation of the endo cyclopentadiene dimer and its inability to recognise Magnesium in the nucleophilic addition to a pyridinium ring experiment. MM2 relies on existing information programmed into the force field, and as a result is usually suitable for calculations involving metals. Additionally, molecules which exhibit non-classical bonding (cf. simple diatomic species) such as multi electron-multi centre bonds (diborane), aromaticity (benzene) and even stereo electronic effects (hyper/sigma conjugation) cannot be modelled using molecular dynamics. A further draw back of molecular mechanics is that it cannot be used for studying reactions, as it does not recognise the breaking/formation of bonds. In such circumstances wavefunction calculations need to be made and a quantum approach must be considered.

Parameterized Model number 3 (PM3) is "a semi-empirical method which allows the quantum calculation of molecular electronic structures. It is based on the Neglect of Differential Diatomic Overlap(NDDO) integral approximation. NDDO adds all two centre integrals for repulsion between a charge distribution on one centre and a charge distribution on another centre. Semi-empirical quantum chemistry methods are based on the Hartree-Fock formalism, but make many approximations and obtain some parameters from empirical data".

This method was developed by J Stewart.

Regioselective Addition of Dichlorocarbene

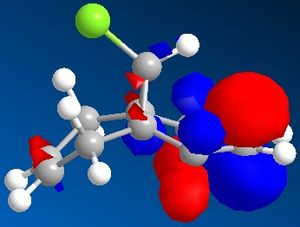
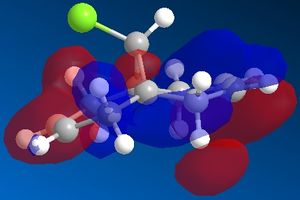
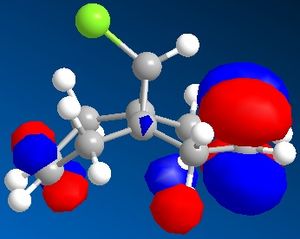
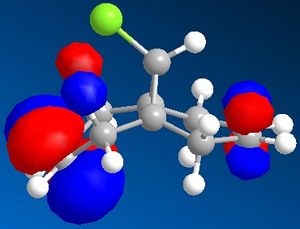
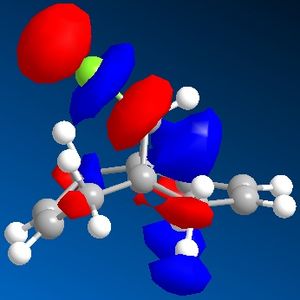
In this section the molecular orbitals of compound 12 can be calculated and visualised. This was intended to be done using PM3, but since this function was not available, Gaussian was used to calculate the molecular orbital instead. Both compound 12 and its monohydrogenated product were submitted to SCAN to run a Guassian calculation which optimized both geometries and also provided IR vibrational frequencies.

Molecule 12(left) and its monohydrogenated product(right)

Compound 12 was sketched and an initial clean up was run using MM2. After this the molecule was optimised using Gaussian, and the molecular surface calculated and displayed. The results are displayed in the table below (isocontour= 0.04 a.u. in accordance with literature).

Molecular Orbitals of Compund 12

HOMO -1	HOMO	LUMO	LUMO +1	LUMO +2

Compound 12 and its monohydrogenated product were optimized using PM3 initially, then submitted to SCAN to run a Gaussian calculation using the following basis set/method:

b3lyp/6-31G(d) opt(maxcycle=20) freq

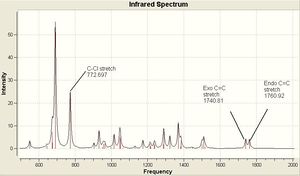
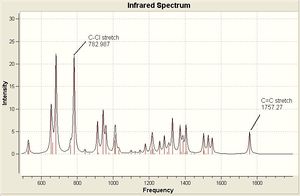
The optimized geometries and vibrational frequencies are displayed below. The IR spectrum has been enlarged to show only the most relevant frequency range (500 - 200- cm^-1) in greater detail.

Molecule	Compound 12		Monohydrogenated Product
C=C Stretching Frequency (cm-1)	1740.81 (Exo - Intensity 4.1475)	1760.92 (Endo - Intensity 3.9104)	1757.27 (Intensity 5.0178)
C-Cl Stretching Frequency (cm-1)	772.697 (Intensity 25.1767)		782.987 (Intensity 22.0896)
IR Spectrum
3D Molecule	Mol_1		Mol_1

The C-Cl vibrational frequency increases from 772.697 cm^-1 to 782.987 cm^-1. This can be rationalised using molecular orbital theory and the MO pictures. In the molecule 12, the exo C=C π orbital interacts with the C-Cl σ* orbital (see HOMO - not visible when isocontour = 0.04 a.u., but it is when isocontour = 0.01 a.u.), which weakens the bond. A weaker bond means less energy is required to cause it to vibrate (see equation), thus lower frequency. By hydrogenating this bond, this destabilising interaction is removed, causing the vibrational frequency to increase. The same reason explains why in molecule 12 the exo C=C vibrational frequency is lower than the endo vibrational frequency.

Structure Based Mini Project using DFT-Based Molecular Orbital Methods

Density functional theory (DFT) is a "quantum mechanical theory used in physics and chemistry to investigate the electronic structure (principally the ground state) of many-body systems, in particular atoms, molecules, and the condensed phases" . This section involves ab initio calculations, which although give greater accuracy and the ability to predict NMR, IR and optical rotation, requires much greater processing power (SCAN).

Assigning Regioisomers in 'Click Chemistry'

This 1,3-dipolar addition to give 1,2,3-triazole has two regioisomers; A and B. Research has reported that under Cu(I) catalysis isomer A predominates, while under Ru(II) catalysis isomer B predominates. This mini-project will use DFT techniques to determine how each isomer can be identified using a spectroscopic techinque, namely whether ¹³C NMR can tell them apart. The predicted ¹³C NMR can then be compared to literature records to confirm whether the predictions are correct.

'Click Chemistry' reaction mechanism

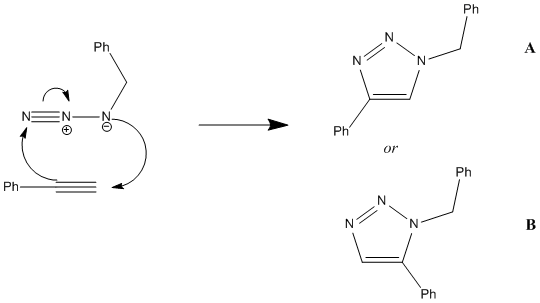
In order to predict the ¹³C NMR both molecules first need to be optimized using DFT via SCAN. The molecules were first sketched in ChemBio3D, then subjected to MM2 and MOPAC/AM1 to quickly optimize their geometries. Since both 1,2,3-triazole are fairly simple molecules, these methods worked quite well and optimiztation using teh Hatree-Fock technique were not necessary. The molecules were then submitted to SCAN using the following Basis Set/method:

mpw1pw91/6-31(d,p) opt(maxcycle=25)

The optimized 1,2,3-triazoles regioisomers are displayed below

DFT Optimized Geometry for A and B 1,2,3-triazoles

1,2,3-triazole A	1,2,3-triazole B
Mol_1	Mol_1

The optimized molecules were then resubmitted to SCAN to predict the NMR. To do this the following basis set/method was used:

mpw1pw91/6-31(d,p) NMR scrf(cpcm,solvent=chloroform)

Click A

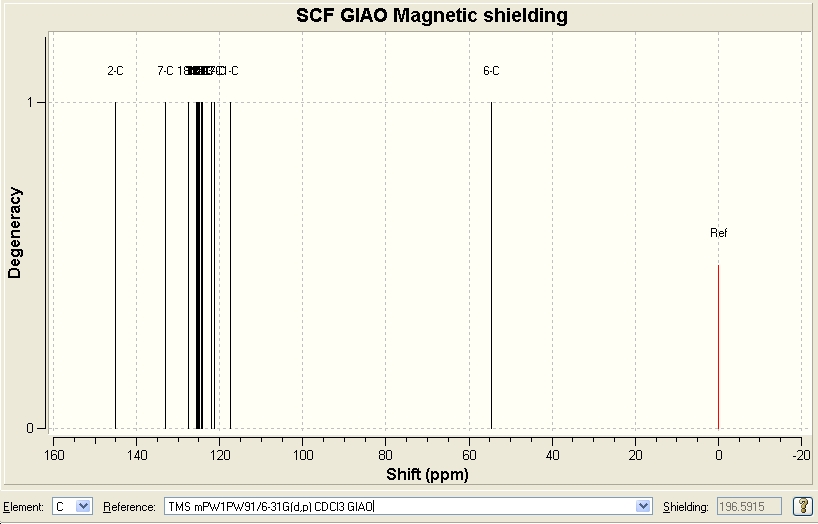
Predicted NMR for A

Comparison between predict and literature chemical shift for isomer A

Predicted Chemical Shift (ppm, δ)	54.3713	117.31	125.571	127.454	133.044	145.18
Literature Chemical Shift (ppm, δ)	54.0	119.5	125.5	127.9	134.6	148.0

Since there were no heavy elements in the molecule, no adjustments were made. The predicted data correlates quite well with the reported values in literature.

Click B

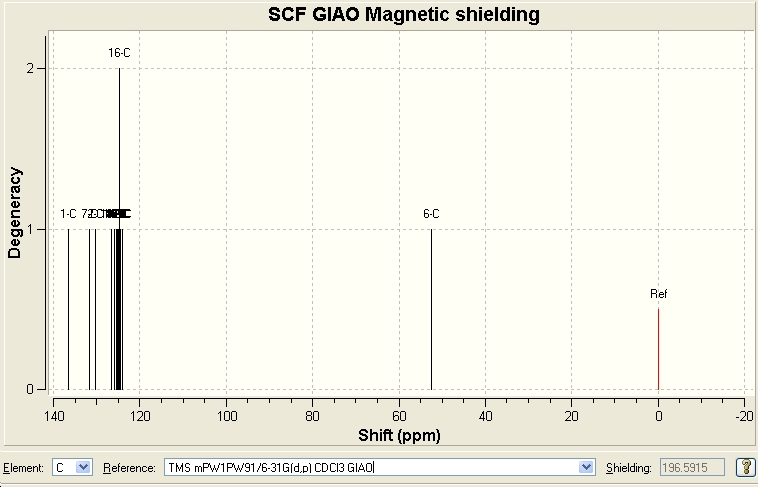
Predicted NMR for B

Comparison between predict and literature chemical shift for isomer B

Predicted Chemical Shift (ppm, δ)	52.3869	126.677	130.197	131.613	136.55
Literature Chemical Shift (ppm, δ)	51.85	126.93	129.64	133.26	138.26

Since there were no heavy elements in the molecule, no adjustments were made. The predicted data correlates quite well with the reported values in literature.

From comparing the NMR spectra for both A and B it is clear that ¹³C NMR is a viable spectroscopic method to differentiate betweeen the two regioisomers. Looking at the original report, it is possible to confirm that the isomer A matches the data in the journal.