Rep:Mod:sp32

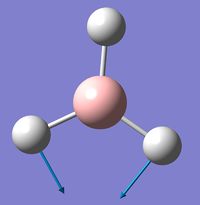
BH3

BH

A structure for BH₃ was drawn in gaussian, before otimisation the bond lengths were set at 1.5 Å. The molecule was optimised using the B3LYP method and 3-21G basis set. The B-H bond length of the optimised structure is 1.17 Å and the bond angle is 120°. A summary of the optimisation is given below:

calculation type	FOPT
Calculation Method	RB3LYP
Basis set	STO-3G
Energy /a.u.	-26.29366780
RMS Gradient Norm /a.u.	0.00000099
Dipole Moment /D	0.00
Point Group	D3H

The gradient is very small, it is very close to zero; this implies that optimisation occurred. Another way to check if optimisation has occurred is to the view the checkpoint file. The checkpoint file showed:

Item Value Threshold Converged?

Maximum Force 0.000002 0.000450 YES

RMS Force 0.000001 0.000300 YES

Maximum Displacement 0.000006 0.001800 YES

RMS Displacement 0.000004 0.001200 YES

Predicted change in Energy=-1.831753D-11

Optimization completed.

-- Stationary point found.

The steps of the optimisation can be depicted in a graphical form.

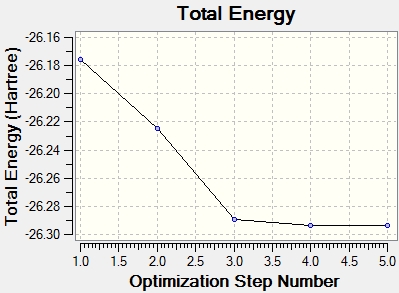
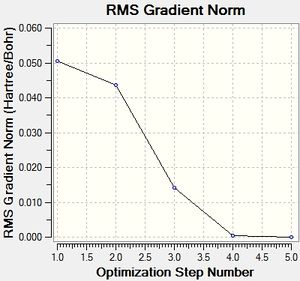
As can be seen from the first graph, the energy decreases with each iteration until its constant. The second graph shows the gradient approaching zero as the energy is minimised. This is because the most stable structure is an energy minimum and at this point the gradient is zero. The structure that is given by the optimisation is only present in real life when there are no other forces constraining the molecule, eg. when it is in the gas phase.

The Molecular orbitals of BH3 where calculated using Gaussian. These can then be compared to the LCAO's to give an idea of how accurate this method is.

caption

Orbital	Symmetry	LCAO	Energy /a.u.
1	a1'	Boron 1S orbital	-6.59
2	a1'		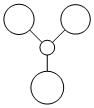-0.41
3	e'		-0.26
4	e'		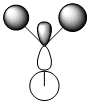-0.26
5	a2		-0.03
6	a1'		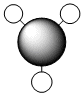0.19
7	e'		0.30
8	e'		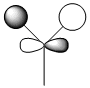0.30

The Natural Bond Orbitals can also be calculated. These can only be viewed in their simplest graphical form in Gaussview. These are shown here:

In the first image the green represents a positive charge and the red a negative charge. The Boron atom is a lewis acid and electron deficient so it a bright green, and the equivalent negative charge is split over the three hydrogens, as this is a neutral molecule, so they are less bright red. This is more clearly shown by the numerical charges.

NBO Analysis takes the electron density of the molecule and splits in into 2e-2c bonds. The table below shows where the electron density in the bonds come from.

caption

	type	percentage from B	percentage from H
1	bond B1-H1	43.2 (s:33.33 p66.67)	56.8 (s:100)
2	bond B1-H2	43.2 (s:33.33 p66.67)	56.8 (s:100)
3	bond B1-H3	43.2 (s:33.33 p66.67)	56.8 (s:100)
4	core	100 (s:100)
5	lone Pair	100 (p:100)
6	anti-bond B1-H1	43.2 (s:33.33 p66.67)	56.8 (s:100)
7	anti-bond B1-H2	43.2 (s:33.33 p66.67)	56.8 (s:100)
8	anti-bond B1-H3	43.2 (s:33.33 p66.67)	56.8 (s:100)

Bonds 1-3 involve sp² orbitals from boron and an s orbitals from Hydrogen and 6-8 are the respective anti bonds. 4 is the 1s orbital of boron and 5 is a p orbital from boron.

The amount of mixing can also been seen by consulting the Section titled: Second Order Perturbation theory analysis of Fock matrix in NBO basis. For BH3 the mixing values are all minimal as little mixing occurs.

The energies of the bonds are also given:

caption

Bond	Occupancy	Energy /kJmol-1
B1-H1	1.97	-7.99 x 102
B1-H2	1.97	-7.99 x 102
B1-H3	1.97	-7.99 x 102
core	2	-1.73 x 104
Lone Pair*	0	8.03 x 101
B1-H1 *	0.03	6.79 x 102
B1-H2 *	0.03	6.79 x 102
B1-H3 *	0.03	6.79 x 102

Using the Linear Combination of Atomic Orbitals, The MO diagram of BH3 looks like:

As can be seen the calculated MO orbitals are similar to the LCA orbitals. The 1s orbital hasn't been drawn on the MO diagram because it is not normally considered as participating in bonding. In the diagram the 3 1S orbitals from the Hydrogens ahve been mixed to give a set of orbitals. In the LCAO diagram the boron orbitals aren't mixed and therefore one of the Molecular Orbitals is just the 2S boron orbital combining with an orbital from the hydrogens, and the other two are the Boron 2p orbitals combining with the Hydrogen orbitals. This doesn't match with the Natural bond analysis.

The vibrations of the molecule can also be calculated using gaussian. A system has 3N-6 Vibrational modes, where N is the number of atoms. For BH3 this means there should be 6 vibrational modes.

	Frequency	Intensity	Description	Symmetry
1	1244.57	126.1	Hydrogens moving along the arrows.	a2
2	1368.18	17.0	Hydrogens move along arrows, one moves more than the others.	e'
3	1368.18	17.0	Two hydrogens bend towards each other.	e'
4	2909.00	0	All hydrogens move outwards.	a'
5	3136.79	10.88	One hydrogen moves towards the boron as the other moves away and vice versa.	e'
6	3136.79	10.88	One hydrogen moves towards the boron as the others move away and vice versa.	e'

These 6 vibrations are depicted as 3 peaks in the Infrared Spectrum, this is because vibrations 2&3 and 5&6 are degenerate so each pair appears as one peak. Vibration 4 is perfectly symmetric so isn't detected by infrared spectroscopy.

Other useful information given by the calculation is the low frequencies. These are the '-6' when calculating the number of vibrational modes. They are the movements of the center of mass of the molecule and should be as close to zero as possible.

TlBr3

TlBr

Thallium is a highly toxic element so many chemists are wary of exopsing themselves to the element. Computations allow chemists to explore the properties of these molecules without handling them. However Thallium is a large atom with 81 electrons and even in a simple compound such as TlBr3, this leads to there being a lot of electrons fro the computer to deal with. This means that using schrodingers equation isn't a viable option. However using psuedo-potentials allow us to model the compound using lots of simpler basis functions that together give a good representation of the actual basis function. Thallium Tribromide was optimised using the B3LYP method and LANL2DZ basis . A summary of the information from the optimisation is below:

calculation type	FOPT
Calculation Method	RB3LYP
Basis set	LANL2DZ
Energy /a.u.	-125.65928160
RMS Gradient Norm /a.u.	0.00000027
Dipole Moment /D	0.00
Point Group	D3H

The gradient is very small, it is very close to zero; this implies that optimisation occurred.As can be seen from the first graph (below), the energy decreases with each iteration until its constant. The second graph shows the gradient approaching zero as the energy is minimised. This is because the most stable structure is an energy minimum and at this point the gradient is zero. The structure that is given by the optimisation is only present in real life when there are no other forces constraining the molecule, eg. when it is in the gas phase.

The optimised bond length of thallium is 2.43Å and the optimised bond angle is 120°. The literature value for a Tl-Br bond length is 2.51Å. The calculated bond length is close enough to consider this a fairly accurate optimised structure.

The vibrational analysi is can also be carried out using Gaussian. The optimisation finds a point on the potential energy surface that has a gradient of zero. This could be a minima but it could also be a transition state maximum. Frequency analyisis uses a second derivative of the PES, so if all the vibrations are positive a minima has been found but if some of the vibrations are negative then a maxima has been found.

	Frequency	Intensity	Description	Symmetry
1	39.32	39.28	Hydrogens move back and forth along the arrows.	e'
2	39.32	39.28	2 of the hydrogens move towards each other, along the arrows.	e'
3	55.50	10.42	all three hydrogens move away from the planar molecule along the arrows towards a bent structure.	a2
4	271.34	0	All three hydrogens away for the boron atom, in the plane of the molecule.	a'
5	313.80	25.56	One hydrogen moves towards the boron as the other two hydrogens move away, in the plane of the molecule, and vice versa.	e'
6	313.80	25.56	One hydrogen moves towards the boron atom as another moves outwards.	e'

the ordering of the vibrations are slightly different compared to BH₃. This is probably due the fact that Tl-Br bonds are polarised, so the Thallium and Bromine are in displaced on a molecular orbital diagram, which would affect the splitting and therfore change the ordering of the orbitals.

Gaussian doesn't show the bonds in this molecule, this is because gaussview has a fixed definition of the length of bonds and if the bond is longer then it isn't drawn in. Inorganic bonds are often longer than organic bonds so it is necessary to check the actual file to find the bonds. In a classical interpretation a bond is the overlap or sharing of electrons , this requires the atoms of the bond to be close enough together for the orbitals to physically overlap, so that the electron can be shared or transferred. Quantum Mechanically a bond is the overlap of the electron wavefunctions, which requires them to be symmetrically compatible.

Cis and Trans Isomers of MO(CO)₄(PPH₃)₂

MO(CO)₄(PPH₃)₂ has two isomers, cis and trans. In the vibrational spectra the cis isomer has 4 carbonyl absorption bands and the trans isomer has 1 carbonyl absorption band. The actual molecule is too complex to compute so the triphenylphosphine ligands are replaced by chlorine ligands. Chlorine atoms are a similar size and behave in a similar manner so are an acceptable replacement.

Cis Isomer

Trans Isomer

Both molecules were optimised at the LANL2MB and then LANL2DZ level

	Cis	Trans
calculation type	FOPT	FOPT
Calculation Method	RB3LYP	RB3LYP
Basis set	LANL2DZ	LANL2DZ
Energy /a.u.	-623.57707188	-623.57603113
Energy /x106kJmol-1	-1.63720	-1.63719
RMS Gradient Norm /a.u.	0.00001047	0.00000079
Dipole Moment /D	1.31	0.30
Point Group	C1	C1

When the molecule was optimised, the frequency analysis was done to ensure that a true minima had been found as oppose to a transition state maxima.

caption

	cis	trans	Literature values
Mo-P bond length /Å	2.53	2.48	2.46 for Mo-P(Me)3
P-Cl bond length /Å	2.24	2.24	2.04 in gas phase
Mo-C bond length /Å	2.06	2.11	2.06 in carbonyl compounds
C-O bond length /Å	1.19	1.19	1.12 in gas phase
Mo-P-Cl Angle /°	120.38, 118.17, 115.99	117.29, 120.34
Cl-P-Cl Angle /°	98.89, 99.38, 110.18	99.46, 99.09
Mo-C-O Angle /°	178.18	179.85

The Trans isomer has the chlorines of the PCl₃ ligand arranged so that The Cis isomer has the chlorines of the PCl₃ ligand arranged so that The trans isomer has longer bonds for the atoms bound to the molybdenum. This is due to the trans effect. Ligands that are trans to each other donate their electrons into the same set of orbitals so can have an effect on the other ligand. PCl3 ligands have a relatively strong trans effect. Structurally this is observed as a stretching of the bonds, which is what is seen in these structures. The Mo-P bond length is close to the literature value, the difference could be explained by the fact that the literature value is for a structure containing PMe₃ as oppose to PCl₃. This could be confirmed by seeing how close a calculated Mo-P(Me)₃ is to the literature value. The value for the Carbonyl bond length is longer than the literature value but this is because binding to the metal center has an effect on the bond. When the carbonyl is bound to the Molybdenum the d electrons of the molybdenum can be donated into the CO π* bond causing it to lengthen. However the increase is only small, so it is unlikely a huge amount of backbonding is occuring, this is probably because PCl₃ is a much stronger π acceptor. The P-Cl bond is a lot longer than the literature vlaue. This could be due backbonding occuring into the P-Cl σ*, as adding electrons to the σ* would unstablise the P-Cl bond, lengthening it. It is possible to confirm that backbonding is occuring in this molecule by looking at the NMR spectrum .

ΔE = Ecis - Etrans = -2.73kJmol^-1. So the trans isomer is more stable. This isn't a particularly large difference in energy, and probably arises due to streric repulsion in the cis compound where the bulky PCl₃ groups are next to each other. This agrees with experimental observations that the cis isomer isomerises to the trans isomer. The isomerisation has been determined to have a dissociative mechanism going via a 5-co-ordinate square planar intermediate, where the remaining phosphine ligand is equatorial. The cis ligand is more likely to dissociate as the PCl3 ligand has a high cis-labilising effect, more so than the carbonyl ligand. The PCl3 ligand then attaches back to the molybdenum atom, preferentially in the trans position, as this minimses steric repulsions.

Cis Isomer

Frequency /cm-1	Intensity	Description
2143.38	154.24	All CO's stretching, both the trans and equitorial pair are symmetrical but the two pairs stretch in opposite directions. The trans CO have a much large stretch
2115.45	207.87	All CO's stretch symmetrically
2114.45	289.86	The axial CO's stretch asymmetrically
2109.42	147.84	The equitorial CO's stretch asymmetrically
419.91	364.13	The main motion is the Phosphorous atoms moving towards and away from the Molybdenum. As one moves in the other moves away.
12.82	0.13	Rotation like movement of the chlorines around the phosporus.
4.18	0.42	Rocking motion of the molecule, the phosphorus atoms and molybdenum remain still.

Trans Isomer

Frequency /cm-1	Intensity	Description
2030.99	3.78	Symmetric stretch of all the CO's
1977.21	0.65	Asymmetric stretch of all the CO's
1950.92	1466.77	Asymmetric stretch of one pair of trans CO's
1950.92	1475.39	Asymmetric stretch of the other pair of trans CO's
408.81	727.66	P-Mo-P stretch, concerted
6.06	0	Cl's rotating around the phosphorus
5.04	0.09	rocking motion around the P-Mo-P bond

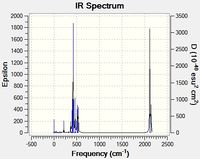
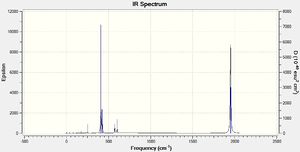Group theory predicts that the Cis isomer will have 4 bands in the IR spectrum and the trans isomer will have 1. The Cis isomer has 4 CO bands in the infrared spectrum, which correspond to the symmetric and assymetric stretches of the axial and equitorail carbonyls. The trans Isomer has 3 bands, one symmetric and one asymmetric with all the carbonyls stretching, and one peak for the two degenterate stretchs of one pair of trans carbonyls stretching. However the stretches where all the carbonyls are moving are not very intense. Group theory predicts that the Cis isomer will have 4 bands and the trans isomer will have 1. High intensity peaks have also been described above for both isomers. Peaks at low frequencies correspond with motions that have a low energy. For instance this could be a torsional rotation around a bond or the breathing modes of the molecule.

Miniproject: Sulfamic acid

Sulfamic Acid

Conjugate Base

Sulfamic acid has the formula H₃NSO₃. The reaction: H₂NSO₂(OH) + NH₂^- ↔ H₂NSO₃^-+ NH₃. The position of the equilibrium can be determined by calculating the energy of each side and calculating the difference in energy. Molecular calculations can then be used to show the orbitals and give an idea of what happens to the electron when the proton is removed.

All the molecules were optimised using the B3LPY method and 6-311g(d,p) basis set and then the frequency analysis was done to ensure a true minima had been found.

Sulfamic Acid, H₂NSO₂(OH):

calculation type	FOPT
Calculation Method	RB3LYP
Basis set	6-311G)d,p)
Energy /a.u.	-680.45609115
Energy / x 105kJmol-1	-17.86
RMS Gradient Norm /a.u.	0.000026
Dipole Moment /D	2.63
Point Group	C1

NH₂^-:

calculation type	FOPT
Calculation Method	RB3LYP
Basis set	6-311G)d,p)
Energy /a.u.	-55.87061313
Energy /x 105kJmol-1	-1.47
RMS Gradient Norm /a.u.	0.024
Dipole Moment /D	1.59
Point Group	C2V

H₂NSO₃^-:

calculation type	FOPT
Calculation Method	RB3LYP
Basis set	6-311G)d,p)
Energy /a.u.	-679.85372011
Energy /x 105kJmol-1	-17.84
RMS Gradient Norm /a.u.	0.052
Dipole Moment /D	5.67
Point Group	C1

NH₃:

calculation type	FOPT
Calculation Method	RB3LYP
Basis set	6-311G)d,p)
Energy /a.u.	-56.57522027
Energy /x 105kJmol-1	-1.48
RMS Gradient Norm /a.u.	0.00737169
Dipole Moment /D	1.54
Point Group	C3V

The energy of the reaction can be dtermined using: ΔE=E_rhs-E_lhs= (E_H2NSO3^- + E_NH3) - (E_H2NSO2(OH) + E_NH2^-) = (-1.48x 10⁵ + -17.84x 10⁵) - ( -1.47x 10⁵ + -17.86x 10⁵) = -19.32x 10⁵ - -19.33x 10⁵ = -268.32 kJmol^-1 This means that the equilibrium position of the reaction is over to the left hand side. The pKa of sulfamic acid is ~1.0, which means slfamic acid is a relatively strong acid, however it is also has low corrosive rates compared to other acids. This might be due to the acid having a zwitterion tautomer. This means that the equlibrium position of the reaction would be different as the tautomer should have a different energy.

The geometry of the acid and its conjugate base can be compared:

caption

bond	Acid /Å	Conjugate base /Å
S-O 1	1.63	1.49
S-O 1	1.45	1.48
S-O 3	1.45	1.48
S-N	1.66	1.76
O-H	0.97	-
N-H	1.01	1.01

In the acid there are two distinct S-O bond lengths, one of which is much shorter than the other and is most likely a double bond. In the conjugate base the S-O bonds are all very similar, which suggests there is conjugation. The S-N bond length in the conjugate base is longer than in the acid, this is due to the negative charge being partially on the Sulphur. The literature values for the acid are:

caption

bond	Length /Å
S-O 1	1.44
S-O 1	1.44
S-O 3	1.44
S-N	1.77
O-H	-
N-H	1.03

These values are from the solid structure which is the zwitterion form, however most are very similar to the calculated values.

The molecular orbitals of the acid and its conjugated base were determined in order to determine what occurs when the hydrogen is lost. Both molecules have 25 filled orbitals, 10 of which are core orbitals of the atoms. Orbitals 10-14 are very similar in bothe molecules and are mostly based around combinations of the oxygen and nitrogen s orbitals. From orbital 15 they become different for the two molecules. However the orbitals that are of interest are the orbitals around the HOMO-LUMO gap.

Orbital	Acid Orbital	Energy	Conjugate base Orbital	Energy
Lumo + 1		0.03631		0.24757
Lumo		-0.00367		0.18930
Homo		-0.31114		-0.06184
Homo - 1		-0.32539		-0.07970
Homo - 2		-0.34380		-0.10416
Homo - 3		-0.37300		-0.11966

The homo of the conjugate base consists of the p oritals of the oxygen atoms, the homo of the acid also involves these orbitals but also involves a p orbital from the nitrogen as well. The lumo's of both molecules are also similar in shape, with the acid having an extra lobe which must result from the hydrogen bonded to the oxygen. However the biggest difference is in the energies. The Lumo of the acid is a bonding orbital, whereas the Lumo of the conjugate base is an antibonding orbital. This means that when the hydrogen is lost and the acid effectively gains a pair of electrons they are still in bonding orbitals, which is why sulfaic acid is a strong acid.

Natural bond analysis, tells us from which atomic orbitals the bonds are made from. For the acid:

Bond
S-O 1	32% S (19%s, 81%p): 68% O (19%s, 81%p)
S-O 2	36% S (28%s, 70%p): 64% O (24%s, 76%p)
S-O 3	36% S (28%s, 70%p): 64% O (24%s, 76%p)
S-N	36% S (29%s, 70%p): 64% N (24%s, 76%p)
O-H	74% O (23%s, 77%p): 25% H (100%s)
N-H	70% N (29%s, 70%p): 30% H (100%s)
O(2,3) lone pairs	100%p x2
O(1) lone pairs	100%p and 58%s, 42%p
N lone pair	15%s, 85% p

For the Conjugate Base:

Bond
S-O 1	35% S (27%s, 71%p): 65% O (24%s, 76%p)
S-O 2	35% S (27%s, 71%p): 65% O (24%s, 76%p)
S-O 3	35% S (27%s, 71%p): 65% O (24%s, 76%p)
S-N	35% S (19%s, 79%p): 64% N (20%s, 80%p)
N-H	67% N (25%s, 75%p): 32% H (100%s)
O lone pairs (each oxygen)	100%p x2 and 77%s, 23%p
N lone pair	28%s, 71% p

In the acid there are two types of S-O bonds, however the difference between them is small. This corresponds to the single and double bonds, but the chances are that at higher temperatures the hydrogen moves between the three oxygens. In the Conjugate base the S-O bonds are all equivalent, which suggests that there is some conjugation. This can be seen from the relative charges of the different atoms:

atom	acid	conjugate base
s	2.37	2.37
O	-0.85	-0.99
O	-0.88	-1.01
O	-0.90	-0.99
H(-O)	0.49	-
N	-1.02	-1.04
H(-N)	0.40	0.33
H(-N)	0.40	0.33

The charge of all the oxygens and not just one has decreased. This can be sen pictorially using gaussview:

The bright green represents positive charge and the red neative charge, for the conjugate base the oxygens are a brighter red.

The Ir spectrum of both were calculated.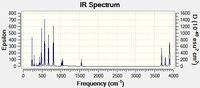

As can be seen they are quite different.

	acid			anion
Motion	frequency	intensity		frequency	intensity
O-H stretch	3902.3	219.21
H-N-H asymmetric stretch	3790.19	79.45		3548.00	0
H-N-H symmetric stretch	3690.19	85.49		3455.58	0.98
H-N-H bend (inwards)	1551.73	32.66		1592.88	26.26
H-N-H bend (outwards)	1081.64	22.96		1093.84	33.34

The stretching vibrations of the acid are higher than those of the Conjugate base but the bending vibrations are higher for the conjugate base. This is probably due to the hydrogen bonding present in the acid. Removing the hydroxy hydrogen means that the nitrogen hydrogens in the conjugate base are freer to stretch away so less energy is needed, but there is no longer an attractive force that would enhance the bending motion, so the energy is higher for this motion.