Rep:Mod:sophia2416
Comp Chem Lab
EX3 Section
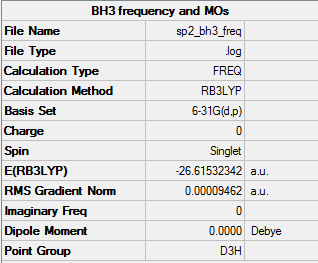
BH3
B3LYP/ 6-31G level (p,d)
Item Value Threshold Converged? Maximum Force 0.000189 0.000450 YES RMS Force 0.000095 0.000300 YES Maximum Displacement 0.000746 0.001800 YES RMS Displacement 0.000373 0.001200 YES Predicted change in Energy=-2.116143D-07
Frequency analysis log fileː
Low frequencies --- -0.2263 -0.1037 -0.0054 47.9770 49.0378 49.0383 Low frequencies --- 1163.7209 1213.6704 1213.6731
BH3 optimised molecule |
IR table
| wavenumber (cm-1 | Intensity (arbitrary units) | symmetry | IR active? | type |
| 1164 | 92.5 | A2 ′ ′ | yes | out-of-plane bend |
| 1214 | 14 | E' | yes | bend |
| 1213 | 14 | E' | yes | asymmetric bend |
| 2580 | 0 | A1 ′ ′ | no | symmetric stretch |
| 2713 | 126 | E' | yes | asymmetric stretch |
| 2713 | 126 | E' | yes | asymmetric stretch |
IR Spectrum
There are 6 vibrations, however in the IR spectrum shown below the vibrations observed are less than 6. This is because there are two degenerate sets, giving 1 signal in the IR spectrum and one vibration which is not IR active
Red annotation in IR Spectrum corresponds to vibration shown in picture belowː

MO Diagram (Using the MO diagram from the linkː http://www.huntresearchgroup.org.uk/teaching/teaching_MOs_year2/P1_BH3_MO_diagram.pdf)

]
The computed MOs (real) match the MO drawings (theoretical) pretty well, except the a'1 antibonding MO where some of the theoretical orbitals drawn(white ones) are found to be smaller than the real ones.
NH3
B3LYP/ 6-31G level (p,d)
Item Value Threshold Converged? Maximum Force 0.000005 0.000450 YES RMS Force 0.000003 0.000300 YES Maximum Displacement 0.000010 0.001800 YES RMS Displacement 0.000007 0.001200 YES Predicted change in Energy=-7.830075D-11 Optimization completed.
Frequency analysis log fileː
Low frequencies --- -11.6527 -11.6490 -0.0041 0.0333 0.1312 25.5724 Low frequencies --- 1089.6616 1694.1736 1694.1736
NH3 optimised molecule |
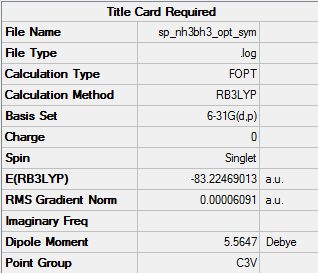
NH3BH3
Item Value Threshold Converged? Maximum Force 0.000124 0.000450 YES RMS Force 0.000057 0.000300 YES Maximum Displacement 0.000472 0.001800 YES RMS Displacement 0.000264 0.001200 YES Predicted change in Energy=-1.577701D-07 Optimization completed.
Frequency analysis log fileː
Low frequencies --- -0.0571 -0.0506 -0.0074 21.3946 21.4048 40.8496 Low frequencies --- 266.0618 632.3619 640.1196
NH3BH3 optimised molecule |
E(NH3)= -26.61531 a.u. (as reported in gaussview)
E(BH3)= -56.55642 a.u. (as reported in gaussview)
E(NH3BH3)= -83.22469 a.u. (as reported in gaussview)
Ng611 (talk) 20:52, 15 May 2018 (BST) I think these values were a bit mixed up
Calculating the association energyː
ΔE=E(NH3BH3)-[E(NH3)+E(BH3)] = -83.22469 - (-26.61531 + -56.55642) = -0.05287 a.u. = -139 kJ/mol
Ng611 (talk) 20:52, 15 May 2018 (BST) Close but off by a little bit
Calculating the dissociation energyː
ΔE=[E(NH3)+E(BH3)]-E(NH3BH3)= (-26.61531 + -56.55642)- ( -83.22469)= 0.05296 a.u. = 139kJ/mol
Ng611 (talk) 20:52, 15 May 2018 (BST) Remember to include a comparison to a (cited) known bond length
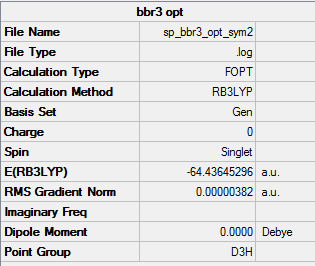
BBr3
B3LYP/ 6-31G level (p,d)
Item Value Threshold Converged? Maximum Force 0.000008 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.000036 0.001800 YES RMS Displacement 0.000023 0.001200 YES Predicted change in Energy=-4.027573D-10 Optimization completed.
Frequency analysis log fileː
Low frequencies --- -0.0137 -0.0064 -0.0046 2.4315 2.4315 4.8421 Low frequencies --- 155.9631 155.9651 267.7052
Br3 optimised molecule |
Aromaticity (Project)
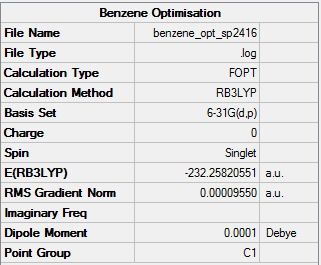
Benzene
B3LYP/ 6-31G level (p,d)
Item Value Threshold Converged? Maximum Force 0.000212 0.000450 YES RMS Force 0.000085 0.000300 YES Maximum Displacement 0.000991 0.001800 YES RMS Displacement 0.000315 0.001200 YES Predicted change in Energy=-5.157444D-07 Optimization completed.
Frequency Analysis Log fileː
Low frequencies --- -17.0537 -14.3774 -9.3919 -0.0005 -0.0003 0.0006 Low frequencies --- 413.7989 414.4772 620.8619
Borazine
B3LYP/ 6-31G level (p,d)
Item Value Threshold Converged? Maximum Force 0.000093 0.000450 YES RMS Force 0.000033 0.000300 YES Maximum Displacement 0.000310 0.001800 YES RMS Displacement 0.000094 0.001200 YES Predicted change in Energy=-1.031287D-07 Optimization completed.
Frequency Analysis Log fileː
Low frequencies --- -17.2021 -10.7823 -6.5358 -0.0005 -0.0003 0.0007 Low frequencies --- 288.8504 289.6721 404.1643
Benzene and Borazine Comparison
Charge Analysis
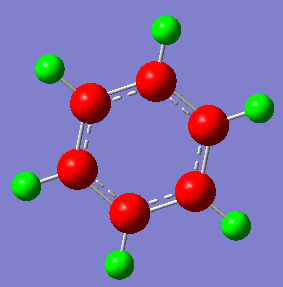
Charge Analysis for Benzene
Atom # NBO Charge
C 1 -0.23852
C 2 -0.23855
C 3 -0.23854
C 4 -0.23852
C 5 -0.23855
C 6 -0.23854
H 7 0.23854
H 8 0.23853
H 9 0.23854
H 10 0.23854
H 11 0.23853
H 12 0.23854
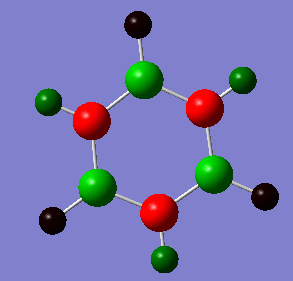
Charges Analysis Borazine
Atom # NBO Charge
H 1 -0.07654
H 2 0.43198
H 3 -0.07655
H 4 0.43198
H 5 -0.07654
H 6 0.43197
N 7 -1.10241
N 8 -1.10240
N 9 -1.10240
B 10 0.74695
B 11 0.74696
B 12 0.74700
Discussion
Benzene and borazine are isoelectronic and isostructural. Both benzene and borazine are considered to be aromatic since they obey the 4n + 2 rule.
As seen in both pictures, the more electronegative atoms are coloured red a whilst the most electropostive ones are coloured green. Black ones, (found only in borazine) share an intermediate charge, some of them are slightly negative whilst some are slightly positive.
In benzene, all the carbon atoms have exactly the same charge (-0.23854) and so do all the hydrogen atoms (0.23854) due to the high symmetry of the molecule. The carbon atoms are more electronegative than the hydrogen atoms due to the delocalised pi ring system.
However, in borazine the more electronegative atoms are the nitrogen ones and the more electropositive the borazine ones. This electronegativity difference makes the bonds to have a greater ionic character than the carbon - carbon bonds in benzene, and hence, borazine has poorer delocalisation than benzene. Benzene is a non-polar while borazine is polar. Additionally, borazine is less symmetric than benzene.
As a result, benzene is non-polar but borazine is polar.
Bonding Analysis

Ng611 (talk) 20:56, 15 May 2018 (BST) A little more comparison is needed here. Which AO comprise these MOs? What's the overall symmetry of the MO (sigma, pi etc.). Why are there differences between the MO's and why do they arise?
Aromaticity
Aromaticity is the property of conjugated cycloalkanes which have enhanced stabilisation. Planar rings that consist resonance bonds exhibit greater stability than other geometric or other arrangements of the same atoms because of aromaticity. This phenomenon is due to delocalisation. It is an ability of the electrons in the π orbitals of the planar carbon atoms, an insight provided by Kekulé. He proposed that there are no alternative C-C and C=C bonds, but instead a greater ring of delocalisation. Hence, describing aromaticity as overlapping pz orbitals is not a good enough description, because of the resonance phenomenon where the electrons resonate around all the elements of the ring.
For a compound to be aromatic the following rules must be obeyedː
1. Compound must be cyclic
2. Huckle's Rule i.e. the ring has to contain 4n+2 p-orbital electrons
3. Each element of the ring must have a perpendicular p-orbital (i.e. the molecule is planar)
If these rules are obeyed, then the molecule is aromatic and has enhanced stabilisation, making it less reactive. The greater stability of these compounds was quantified by heats of hydrogenation (calorimetry). Additionally, X-ray data showed that all carbon bonds share the same length, an intermediate size between a single and a double bond. In proton NMR, aromatic compounds appear to give peaks in a range of chemical shifts, as any protons outside the ring experience deshielding (giving peaks more downflied), and any protons inside the ring are shielded, (giving peaks more upfield).
MO Theory for benzeneː
Using Linear Combination of Atomic Orbtals (LCAO), the s-bonding framework is formed from sp2 hybridised carbon atoms, leaving a p-orbital on each of the 6 C atoms orthogonal to the ring. These 6 atomic p-orbitals (AOs) give 6 molecular orbitals (MOs). The 6 electrons present are placed in the 3 lowest energy MOs (Aufbau Principle), creating the bonding orbitals, leaving 3 MOs empty- the anti-bonding ones. When the phases of the p-orbitals are the same, a common like-phase region is generated, lowering the energy of the MO. Hence, the lowest energy MO is the one where all the π orbitals are in-phase and is named π1.
Ng611 (talk) 21:06, 15 May 2018 (BST) Good explanation. Ideally, I'd like to see this discussion added to a bit with some text regarding modern interpretations of aromaticity, linking back to your MO analysis.
Ng611 (talk) 21:06, 15 May 2018 (BST) Good report. I would add a few more bits and pieces regarding the MO analysis and aromaticity. Your first section, with the exception of your association energy, was excellent.
The real MOs for benzene can represent the concept of aromaticity quite well, representing the π electron density like a doughnut-shaped region, above and below the plane of the ring. They show the combinations of in-phase and out-of-phase of the π orbitals, emphasising the constructive and destructive wavefunctions that describe the orbital, as shown in the above pictures. The more the destructive regions present, the more the nodes present and hence the MO is higher in energy, and possibly anti-bonding. Also, the real MOs show the symmetry of the molecule
Aromaticity for borazine
Borazine has a similar structure to benzene and has similar properties. For example, all the N-B bond lengths are equal and has 6p electrons, which obeys the 4n + 2 rule. However, it can be considered to have poorer aromaticity than benzene due to electronegativity difference between the boron and nitrogen atoms. This causes a dipole and an ionic character in the compound, hence making the pi electron delocalisation poorer. Additionally, NBO analysis suggests weak aromaticity in borazine, as the charge difference displaces the B and N atoms slightly from the nuclear axes.