Jump to content

Rep:Mod:snowball0702

From ChemWiki

Introduction

This module attempts to use computaional methods to find out information about the structures, properties and reactivities of various molecules. As with experimental techniques there is an associated degree of error with the calculated values. These are as follows:

  • energy: 1kJ mol-1
  • dipole moment: 0.01 Debye
  • bond lengths: 0.01
  • bond angles: 0.1o

Gaussian calculates energy values in hartree (a.u.) which is approximately equal to 2625kJ mol-1

BCl3 and Chloroform

In this section the B3LYP method and LANL2MB basis set was used to optomise the geometries and obtain information about BCl3 and chloroform (CHCl3). For BCl3 (shown below) the B-Cl bond calculated distances are 1.87Å and the Cl-B-Cl bond angles are 120o. The molecule has D3h symmetry and an energy of -182,312 kJ mol-1 (-69.439 hartree). 

File type:  .log
Calc type: FOPT
Calc method: RB3LYP
Basis set: LANL2MB
E(RB+HF+LYP): -69.43928112AU
RMS Gradient Norm: 0.00005905 AU
DIPOLE MOMENT: 0 DEBYE
POINT GROUP: D3H

The calculated bond lengths for chloroform are 1.11Å (C-H) and 1.92Å (C-Cl) with bond anles of 108.2o (H-C-Cl) and 110.7o (Cl-C-Cl). The molecule has C3V symmetry and a total energy of -217,993kJ mol-1 (-83.029 hartree). 

 Calc type: FOPT
Calc method: RB3LYP
Basis set: LANL2MB
E(RB+HF+LYP): -83.02872174AU
RMS Gradient Norm: 0.00004239AU
DIPOLE MOMENT: 2.1108 DEBYE
POINT GROUP: C3V
TIME: 24.0 SEC

BH3

Vibrations

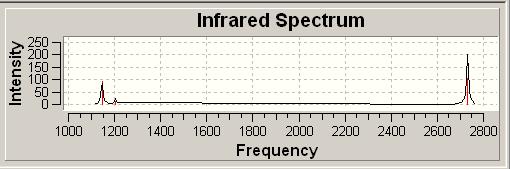
The vibrational frequencies of BH3 were calculated using the B3YLP method and the 3-21G basis set. The results are summarised in the table below.

No. Form of vibration Frequency Intensity Symmetry
1 All H's move parrallel to z axis 1145.71 92.6991 A"2
2 Two H's move towards each other within the plane of the molecule. 1204.66 12.3789 E'
3 All H's are displaced within the plane of the molecule with one moving significantly more than the other two. 1204.66 12.3814 E'
4 All B-H bonds stretch (completely symmetric). 2592.79 0 A'
5 One B-H stretch outwards and one inwards. 2731.31 103.837 E'
6 Two B-H stretches outwards, one inwards. 2731.31 103.83 E'

There are six computed vibrations, however in the predicted IR spectrum there are only three peaks. Firstly the A' stretching frequency does not show up in the spectrum as it is symmetric and does not result in a change of the molecules dipole moment, making it IR inactive. Secondly there are two sets (four vibrations in total) of E' vibrations with each set consisting of two degenerate vibrations, therefore these will only show two peaks in total as the vibrations overlap completely.

Molecular Orbitals

A molecular orbiatl diagaram is shown above[1] (note the 1a' orbital is missing, this relates to the non bonding 1s orbital on the boron atom. The table below shows the first seven MO's generated from the frequency calculation in the previous section. It can be seen claerly that MO 1 relates to an s orbital on the boron atom (1a') and that MO 2 is a fully bonding orbital without nodal planes (2a'). MOs 3 and 4 being of equal energy represnt the 1e' pair and have similar shapes to those predicted, as does 5 which exactly matchs the non bonding p orbital 1a". However MOs 6 and 7 show a degenerate pair instead of the single orbital (3a1') predicted. This pair clearly relates to the 2e' orbitals in the diagram, the calaculation just prdicts them to be lower in energy than 3a1'. This shows that whilst MO theory is useful for giving a rough approximation of the energy levels of a molecule it does not always get the ordering right which is why calculations like the ones performed here are necessary.

The relative energies show that orbitals 1-5 are bonding in nature (negative energy) whereas orbitals 6 and 7 are antibonding. This is significant because orbital 5 is the LUMO as such governs the reactivity of the molecule. The results indicate that bond formation is energetically favourable and in fact BH3 is known to act as a lewis acid that will readily dimerise or form dative bonds with its solvent. This is aided by the molecules planar nature as the LUMO is orientated above and below this plane (as can be seen in the image) without any steric protection allowing for easy attack by a Lewis base.

No. MO Relative Energy No. MO Relative Energy
1 -6.730 4 -0.356
2 -0.517 5 -0.074
3 -0.356 6 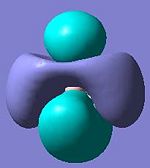0.188
7 0.188

Organometallic Complex

In this section computational modeling was used to predict the IR spectra of cis and trans Mo(CO)4(pip)2. The structures were first optimised using the B3YLP method and the LANL2MB basis set, then with the LANL2-DZ set and finally the frequencies calculated. The piperidine ligand was preoptimised with the 321G basis set.

Trans Isomer

The trans isomer has C1 symmetry and an energy of -2,686,861kJ mol-1. The IR spectrum shows one peak that is significantly larger than any of the others. This is in fact two peaks with close frequencies superimposed, both peaks relating to the CO stretchs (see table below), with one due to outwards stretching and the other due to inwards stretching. It is clear that the similar nature of these vibrations is responsible for their close frequencies.

Form of vibration Frequency Intensity
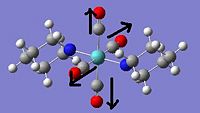
1897 1973
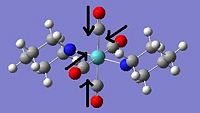
1902 1671

Optimised structure: http://hdl.handle.net/10042/to-1930

Frequency: http://hdl.handle.net/10042/to-1931

Cis Isomer

Despite repeated attempts, Gaussian would not calculate the IR spectrum of the cis isomer. In theory it would be expected to possess the two CO vibrations found in the trans IR plus one other CO vibration relating to assymetric stretching. The reason that this is not present in the trans isomer is that the CO groups are all have equivalent symmetry whereas in the cis isomer the axial and equatorial COs are chemically distinct.

The cis isomer possessses C1 symmetry and an enrgy of -26868866kJ mol-1. This is 5kJ mol-1 lower in energy than the trans isomer. One would expect, however, that the cis isomer was higher in energy due to the increased steric interaction of the two piperidine ligands. It could be that the two ligands under some sort of stabalising interaction, however it is more than likely that this is a flaw within the calculation.

Optimised structure: http://hdl.handle.net/10042/to-193

Ammonia

Introduction

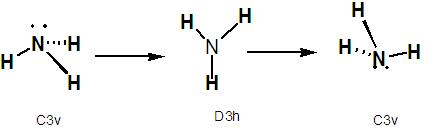
Ammonia is able to invert itself through a process known as pyramidal inversion [2] whereby the hydrogen atoms quantum tunnel through the central nitrogen atom. The ammonia molecule has C3V symmetry but passes through a transition state that is D3h(see below).

Symmetry

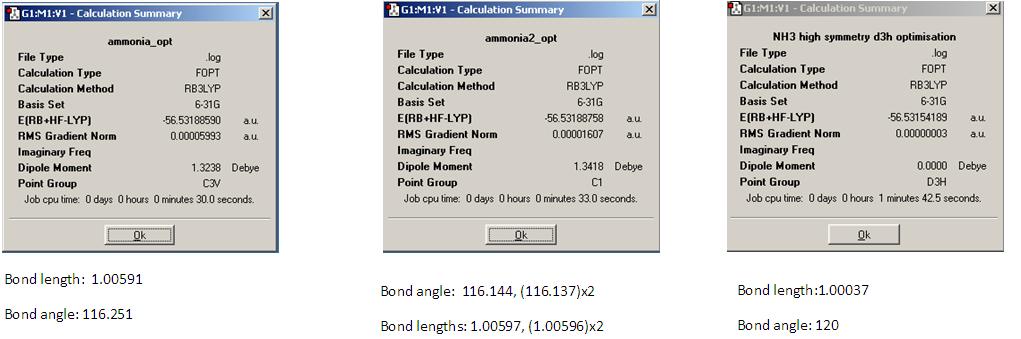
In this section the geometry of ammonia was optimised using the B3YLP method and the 631G basis set for several different symmetries (C1, C3V, D3h). The results of this can be found below.

It can be seen from the above results that symmetry does effect the structure of the molecule, as both the C1 and C3V molecules are bent but the D3h is planar and there are differant bond lengths and bond angles obtained. The symmetry of the molecule also effects the time it takes to run the calculation as the D3h geometry took significantly longer to optimise than the other two. This may be due to the fact the D3h point group possesses many more symmetry elements than the other and as such it takes more computational time to run throuh all of these. If the symmetry of the molecule has not be constrained by system, it should theorectically be able to be broken during the optimisation as this may allow the molecule to go to a more energetically favourable geometry. As can be seen above the lowest energy structure is the C1 geometry. The C3V geometry has an energy differance of 4.4x10-3kJ mol-1 and the the D3h of 0.907. Neither of these can be consider significant as enrgies calculated in Gaussian have an error value of approximately 1kJ mol-1. The bond lengths and angles in the C3v structure are not far from the experimental values[3] of 1.012Å and 112.14o

Using Different Methods

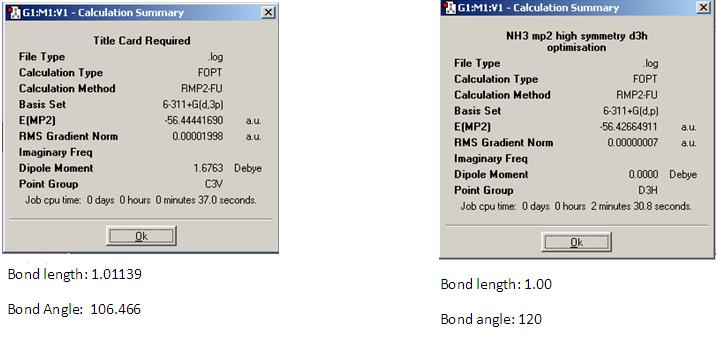
In this section the C3V and D3h geometries were optimised using the MP2 method and the 6311G(d,p) basis set. The results of this can be seen below.

As can be seen from the results, increasing the level of complexity of the calculation also increases the time taken. For the C3V symmetry this was merely an increase of seven seconds but for D3h it was forty seven seconds longer. This shows that the more information the system has to deal with (symmetry or basis sets) the longer the computational time will be. The differance in energy between the C3V and D3h geometries represents the activation barrier for the inversion process. At the 6311g(d,p) level this is ΔE=47kJ mol-1 compared to the value of 0.9kJ mol-1 obtained at the 631G level. The experimetally determined value of 24.2 kJ mol-1 [4] lies between these two values indicating that the model may need refining.

The Inversion Path

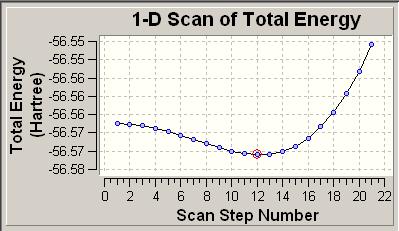
In order to find the barrier to inversion, the saddle point of the potential energy surface must be found. In this section gaussian was used to follow the path of inversion and plot the potentail energy surface (see below.

The lowest energy relates to the C3v symmetry which is -56.5760 hartree (-148,540kJ mol-1).

The D3h geometry is given at the the far left of the curve and has an energy of -56.5657 hartree (-148,513kj mol-1). The highset energy geometry relates to molecule shown below right.

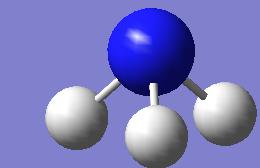
The inversion pathway can thus be view as the transition from the lowest energy geometry C3v to the inverted geometry of an equal energy proceeding via the D3h maxima. This maxima represents the activation barrier (saddle ponit) for the transition and has a value of 27 kJ mol-1 which is significantly closer to the experimental value than the results in the previous section.

Vibrations

The vibrational frequencies of both the C3v and D3h geometries were calculated using the structures optimised at the 631G level. The table below shows the vibrations of the C3v form.

No. Form of vibration Frequency Intensity
1 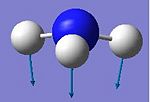452.302 599.472
2 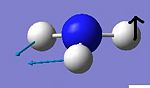1680.47 41.7256
3 1680.47 41.7245
4 3575.43 0.0688
5 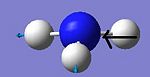3775.76 7.0892
6 3775.76 7.0884

The C3v form shows six positive frequencies whereas the D3h shows five postive frequencies and one negative. This negative frequency (-796cm-1) corresponds to the inversion pathway as it shows all three hydrogens moving parrallel to the z axis. At first glance the C3v vibration at 452cm-1 also appears to relate to this, however it is misleading as at no point in the vibration does the molecule possess D3h symmetry.

Miniproject

Introduction

Ammonia-borane is a molecule of significant current interest due to its potential role as a hydrogen storage molecule for use in carbon-free fuel. Its high hydrogen content, low molecular weight and high density suit it well to use as a vehicle fuel. In this section a variety of computational modeling techniques are used to provide information about the structure, properties and reactivity of ammonia-borane.

Geometry and Comparison with Ethane

Free rotation about the B-N bond allows ammonia-borane to possess an infinate number of conformers, however of these only the staggered (dihedral angle =0o) and the eclipsed (30o) are of interest. The geometry of the staggered conformer was optimised using the B3YLP method and a variety of basis sets, starting with 3-21G and increasing complexity (using the resultant geometry of the previous set as a starting point in each case). The resultant geometry was then altered to the eclipsed conformer using the modify duhedral angle function (i.e angle set to 0)and the energy calculated using the same basis set. This model assumes that the staggered and eclipsed conformers differ only in their dihedral angles and that the bond lengths do not change The table below displays the bond lengths, energies and dipoles obtained.


Basis Set B-N /Å N-H /Å B-H /Å Energy (staggered) /kJ mol-1 Dipole (staggered) /Deybe Energy (eclipsed) /kJ mol-1 Dipole (eclipsed) /Debye
3-21G 1.69 1.03 1.21 -217,303 5.85 -217,295 5.92
631G 1.68 1.02 1.21 -218,426 5.69 -218,418 5.77
6311G(d,p) 1.67 1.02 1.21 -218,571 5.51 -218,561 5.63

It can be seen from the table, the bond lengths, energies and dipoles decrease in value as the complexity of the basis set increases. Comaprison wi experimental results (B-N: 1.673Å, B-H: 1.163Å, N-H: 1.032Å)[5] shows that there is good agreement for the B-N and N-H bonds, however the calculated B-H bond is approximately 0.05Å too long. The staggered conformer is always lowest in energy and at the highest level of calculation (the 6311G(d,p)basis set) there is an energy differance of 10kJ mol-1 between the two conformers. This is due to the steric clash of the hydrogens which is highest in the eclipsed conformer. Thus the molecule will spend the majority of its time in the lower energy, staggered conformation.

Ammonia-borane is isoelectric to ethane yet displays differant properties. The geometries of ethane's staggered and eclipsed conformers were modelled at the 6311G(d,p) level via preoptimisation at 3-21G and 631G in a similar fashion to ammonia-borane. Below is the resultant data for the highest level of calculation. It can be seen that the staggered conformer is agaian prefferedd but with a higher enegy differance (13kJ mol-1). This is due to the electronegativity differance of nitrogen and boron which can be seen in the large dipole 5.51/5.63 Debye compared to that of 0 in ethane. The electronegative nitrogen possesses protic hydrogen and the elctropostive boron has hydridic hydrogens, therefore the eclipsed conformer will be slightly stabalised by the attractive interaction between the two types of hydrogen, off setting the steric repulsion slightly and decreasing the enrergy differance of the two conformers. In comparison ethane possesses only one type of hydrogen and the C-H bond is largely non polar so there is no stabilsing factor for the eclipsed conformer. 

C-C: 1.53Å
C-H: 1.09Å
Energy (staggered): -209,617 kJ mol<sup>-1</sup>
Dipole (staggered): 0
Energy (eclipsed): -209,604 kJ mol<sup>-1</sup>
Dipole (eclipsed): 0

Ethane is a gas at room temperature whereas ammonia-borane is a solid with a high melting point (110-114oC). This is due to ammonia-boranes high dipole moment giving rise to strong intermolecular attraction. In contrast ethane has a neglible dipole moment and as such intermolecular attraction is largely dependant upon much weaker van der Waals forces. The previously mention BH---HN attraction, this time occuring between different molecules, is another form of intermolecular attraction and is known to offer a stabalise the solid by 90.4 kJ mol -1 [6].

intermolecular bonding in ammonia-borane[7]

Formation

Ammonia-borane can be synthesised via the reaction of NH4Cl and NaBH4[8] producing NaCl and H2 in the process. The energies of the reactants and H2 were calculated up to the 6311G(d,p) level and using the previously calculated energies of ammonia-borane (staggered conformer) values for ΔE were obtained. It was assume that the solvated Na+ and Cl- ions being present in both the starting material and products would have zero net contribution to the energy differance. The table below shows the results of this model.

Basis Set NH4+ BH4- H2 Energy (reactants) Energy (products) ΔE
3-21G -148,875 -70,757 -3,073 -219,632 -220,376 744
631G -149,686 -71,137 -3,086 -220,823 -221,512 689
6311G(d,p) -149,840 -71,184 -3097 -221,024 -221,668 644

The results show that the products are energetically favoured by 644kJ mol-1, at the highest level of computation and thus the reaction is exothermic. The release of hydrogen gas indicates that there is an increase in entropy and thus one would expect the reaction to occur spontaneously. Whilst this does not, however, take into account the kinetic activation barrier of the reaction, it should be noted that in the littereature the synthesis had tobe carried out at -78oC which would agree with the prediction of a sponataneous and exothermic process.

Dehydrogenation

Ammonia-borane's usefullness as a hydrogen storage molecule depends both upon its high hydrogen content and upon its ability to release that stored hydrogen under certain conditions. Release at too low a temperature would required a costly cooling system for transportation and storage whilst release at too high a temperature would require some sort of in vehicle heating system. It would be preferable to have the molecule release hydrogen at a temperature above room temperature but less than 350K so as to use waste heat from the fuel cell[9].

Dehydrogenation occurs in three successive steps (see above), releasing up to 3 moles of hydrogen in total. In this section the energies of the products of each of these steps were calculated using the B3YLP method and 63111G (d,p) basis set (via preoptimisation at 3-21G and 631G levels). Using the previously calculated values for ammonia-borane and hydrogen ΔE was calculated for ecah dehydrogenation step. The table below shows the results.

Product Point Group Dipole /Debye Energy /kJ mol-1 ΔE /kJ mol-1
amino-borane C2V 2.09 -215,479 -3
imino-borane C*V 0.21 -212,225 -157
BN C*V 3.03 -208,481 -647

The results show that for all three steps energy must be put into the system in order to release hydrogen gas (i.e. endothermic process) and that this amount of energy increases significantly as more hydrogen is lost. This model does not take into account any entropic contribution to dehydrogenation, though as the molecule is stable at room temperature it can be said that these processes are not thermodynamically spontaneous. The value of ΔE for the first dehydrogenation step is noticabley low and one would therefore assume that the stability of ammonia-borane is due to a large activation barrier. Experimentally ammonia-borane is known to release hydrogen at temperatures above 340K [10] which would appear to agree with this. Due to this high temperature requirement a catalyst is often employed[11].

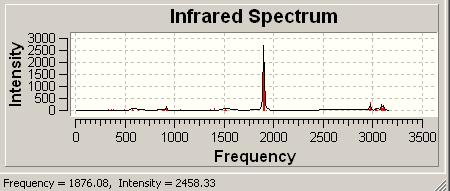
IR and Molecular Orbitals

In this section the vibrational frequencies and molecular orbitals of ammonia-borane were calculated using the 6311G(d,p) optimised, staggered conformer as a starting point. 

B-N stretch:  602.39
N-H bends:  1189.79, 1190.23, 1190.5
B-H bends:  1291.54, 1667.93, 1668.1
N-H stretches : 2420.29, 2468.55, 2468.6
B-H stretches: 3426.13, 3542.89, 3543.06

The predicted IR spectrum can be seen above. There were 18 frequencies in total and the key ones have been noted.

A total of 30 molecular orbitals were calculated. It is beyond the scope of this project to look at them all so only the five around the frontier orbital set have been included in the table below (HOMO -1 is a degenerate pair so two MOs have been given here). An image of the molecule in the same orientation without the MOs has been given to help clarify the location of the orbitals.

MO Image Relative Energy
LUMO +1 0.031
LUMO -0.050
HOMO -0.420
HOMO-1 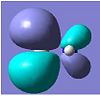-0.420
ref

The LUMO is slightly negative in value indicating that a bonding interaction would be energetically favourable. The catalytic dehydrogenation is known to proceed via an intermediate that has both an ammonia and a borane hydrogen coordinated to the metal centre[12] which would not occur if the LUMO was positive (unfavourable interaction).

References

  1. ↑ http://www.ch.ic.ac.uk/hunt/teaching/teaching_MOs_year2/L3_Tut_MO_diagram_BH3.pdf
  2. ↑ P. Schwerdtfeger, L.J. Laakkonen and P. Pyykko. J. Chem. Phys. , 1992, 6, 680; DOI:10.1063/1.462570
  3. ↑ J. D. Swalen and James A. Ibers, J. Chem. Phys. 36, 1914 (1962); DOI:10.1063/1.1701290
  4. ↑ J. D. Swalen and James A. Ibers, J. Chem. Phys. 36, 1914 (1962); DOI:10.1063/1.1701290
  5. ↑ R. D. Suenram, L. R. Thorne, Chem Phys Letters, Volume 78, Issue 1, 1981, Pages 157-160; DOI:10.1016/0009-2614(81)85575-3
  6. ↑ Frances H. Stephens, Vincent Pons and R. Tom Baker Dalton Trans, 2007, 2613-2626; DOI:10.1039/b703053c
  7. ↑ Klooster, W.T.; Koetzle, T. F.; Siegbahn, P. E. M.; Richardson, T. B.; Crabtree, R. H. (1999), Journal of the American Chemical Society, 121: pp. 6337–6343, DOI:10.1021/ja9825332
  8. ↑ David J. Heldebrant, Abhi Karkamkar, John C. Linehan and Tom Autrey, Energy Environ. Sci., 2008, 1, 156 DOI:10.1039/b808865a 10.1039/b808865a
  9. ↑ T. Marder, Angew. Chem. Int. Ed. 2007, 46, 8116; DOI:10.1002/anie.200703150
  10. ↑ F. Baitalow, J. Baumann, G. Wolfa, K. Jaenicke-Ro¨ßler, G. Leitner Thermochimica Acta Volume 391, Issues 1-2, 12 August 2002, Pages 159-168 DOI:10.1016/S0040-6031(02)00173-9
  11. ↑ Stephens et al, Angewandte Chemie International Edition, Volume 46, Issue 5, Pages 746-749; DOI:10.1002/anie.200603285
  12. ↑ Ankan Paul, Dr. *, Charles B. Musgrave, Prof. Dr., Angewandte Chemie International Edition Volume 46 Issue 43, Pages 8153 - 8156;DOI:10.1002/anie.200702886
Retrieved from "https://chemwiki.ch.ic.ac.uk/index.php?title=Rep:Mod:snowball0702&oldid=820848"