Rep:Mod:smw415TS
Transition States via Computational Methods
Introduction
This study was carried out to analyse Molecular orbitals, reaction kinetics and thermodynamics of different pericyclic reactions
A potential energy surface is plot or a mathematical function that represents the potential energy of a chemical system as a function of multiple reaction coordinates. The number of dimensions of such surface is given by 3N-6 where N is the number of atoms considered in the molecular system. The first derivative relates to the force acting on atoms whereas the second derivative which determines the curvature relates to the force constant, k. The value of k obtained can be used to calculate the vibrational frequency of each 3N-6 mode.
A minimum point, with a positive second derivative, along the reaction coordinate represents a stable species which could be either a reactant, product or an intermediate of the reaction. A transition state (TS) is related to a maximum point (negative second derivative) along a reaction coordinate. A TS is a first order saddle point on a potential energy surface and always has one dimension of the negative curvature. This could be obtained by diagonalising the force constant and by evaluating the Eigen values.
Nf710 (talk) 09:26, 23 March 2018 (UTC) Some confusion here. You diaginalise the Hessian matrix which is the gives you the force constants which are the eigen values and the eigen vectors which are the normal modes which are linear combinations of he degrees of freedom.
In this exercise, two different optimisation methods were used; the semi-empirical route with PM6 and the density functional theory (DFT), B3LYP. These methods are based on the Hartree-Fock model which calculates electron-electron interactions by the assumption that any electron in the chemical system experiences an average field from other electrons. The PM6 method is faster as it uses pre-calculated empirical data to determine the electron density. The B3LYP uses the basis set 6-31(G) which includes the atomic orbitals that make up the molecular orbitals using the theory of Linear Combination of Atomic Orbitals (LCAO). These methods can solve the time-independant Schrödinger equation along the reaction coordinate in order to calculate the energy of the system at each point as well as the first and second derivatives of the energy. These produces optimised geometries which is either a stable species in the reacion (a minimum point with a positive second derivative) or a transition state.
Nf710 (talk) 09:28, 23 March 2018 (UTC) Some confusion here. PM6 is based on the HF hamiltonian but B3LYP is a DFT hamitonian which works with e- density and has a term which uses the HF energy (exchange correlation).
The Gaussian software was used to find the TS of the reaction given below and three different methods were used. The guess TS of could be optimised directly however previous knowledge of the TS was required and this method is the most unreliable even though it is the fastest. Another method employed involved generating the guess TS and then freezing the reacting atoms which also required previous knowledge of the TS however it was more reliable and at the same time it was considered a relatively faster method. The final method started from either the reactants and product, then altering bond lengths and again freezing atoms. This was considered the most reliable method and it did not require any knowledge of the TS but the disadvantages were that it required additional steps and if the minimum point does not resemble the TS geometry, the method would not work.
[4+2] Cycloaddition of ethene and butadiene
(Fv611 (talk) The log files are missing but the MO diagram is good. Your bond length analysis is missing a discussion on the most important bonds (the one being formed at the transition state), which length you have not reported.)
For this Diels Alder reaction (Figure 1), the reactants were separately optimised to a minimum, the structures placed in correct geometry and the distance between reacting atoms were frozen at 2.2 Â. This structure was optimised to a minimum and then to the TS. The product was separately optimised at PM6 level.
MO Diagram of the Transition State

The MO diagram illustrates how the MOs of the reactants, ethylene and butadiene, combine at the transition state. The IRC calculation for the optimised TS and the log file initial frame corresponding to the reactants, was run to make the relative energies of reactants and the optimised TS comparable. As shown in the MO diagram, the MOs of TS is quite high in energy compared to the reactant species since the TS represents the highest energy point in the reaction coordinate. Therefore the theoretical activated species should be destabilised compared to the reactants.
HOMO and LUMO of reactants and optmised TS
The following table shows the HOMO and LUMO of ethylene and butadiene (optimised to a minimum with PM6) as well as the four MOs of the transition state resulting from the linear combination of frontier MOs of the reactants. The HOMO-1 (MO16) and LUMO+1 (MO19) result from the constructive (in-phase) and destructive (out-of-phase) interference respectively, between the HOMO of butadiene and the LUMO of ethylene. The HOMO (MO17) and LUMO (MO18) results from the constructive and destructive interference respectively, between HOMO of ethylene and LUMO of butadiene. The resulting MOs of the optimised TS agrees with the MO diagram drawn above and as well as the principle of conservation of orbital symmetry. The presence of MOs resulting from symmetric-symmetric or asymmetric-asymmetric interactions and the absence of symmetric-asymmetric interactions could be explained using the overlap integral. The overlap between orbitals of different symmetry results in an equal amounts of in-phase and out-of-phase interactions, producing an overall overlap integral of zero. The overlap of orbitals of same symmetry results in either a net in-phase (Positive) or out-of-phase (negative) overlap, therefore the overlap integral is not zero. The HOMO (butadiene) and LUMO (ethylene) are asymmetric, therefore they linearly combine to produce MO16 and MO19 whereas both LUMO (Butadiene) and HOMO (ethylene) are symmetric and combine to produce MO17 and MO18 of the optimised TS.
| Name | MO Image |
|---|---|
| HOMO (Ethylene) | 
|
| LUMO (Ethylene) | 
|
| HOMO (Butadiene) | 
|
| LUMO (Butadiene) | 
|
| HOMO (TS) | 
|
| HOMO-1 (TS) | 
|
| LUMO (TS) | 
|
| LUMO+1 (TS) | 
|
C-C Bond Lengths of optimised reactants, TS and product
The following table shows the bond lengths calculated for the above mentioned species.
| Optimised Structure | C=C (Ethylene) | C=C (Terminal Butadiene) | C=C (Butadiene centre) | C-C (Newly Formed) |
|---|---|---|---|---|
| Reactants | 1.33 | 1.34 | 1.47 | - |
| TS | 1.39 | 1.38 | 1.41 | - |
| Product | 1.53 | 1.50 | 1.34 | 1.54 |
In Diels Alder reactions, the hybridisation of the reacting species changes. The typical C-C bond lengths of different levels of carbon hybridisation are given below,
C(sp3)-C(sp3) = 1.54 Å
C(sp2)-C(sp2) = 1.34 Å
C(sp3)-C(sp2) = 1.50 Å
C atom (Van der Waal radius) = 1.70 Å
The C-C bond lengths of the optimised produce and reactants agrees with the values given above. The carbons of ethylene (dienophile) undergoes a change in hybridisation from sp3 to sp2 which can be confirmed by the length of the same bond being 1.38 Å at the optimised TS which is between 1.54 (sp3-(sp3) and 1.34 (sp2-(sp2). The same explanation could be used to describe the changes in the bond length of terminal C-C bonds of butadiene. The distance between interacting atoms in the TS is lower than 1.70 Å (C-Van der Waal radius) which confirms the interaction between the reacting atoms at the TS. The central C-C bond of butadiene changes from sp3 to sp2 in cyclohexene. This is confirmed by the intermediate bond length of 1.41 Å in the TS. All the bond lengths in the TS consists of values which are in between the values of the corresponding bond lengths of reactants and product.
Vibration at the reaction path of Transition State
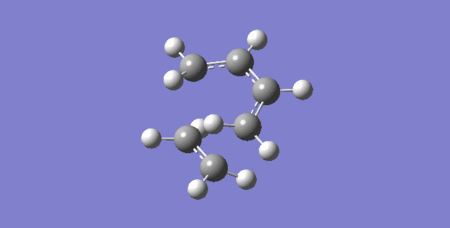
The above vibration relates to a negative frequency value of -949.30 cm-1. The frequency is negative because the force constant is negative at the TS as the energy is maximum, which produces a negative value for the second derivative which is related to the force constant. The above animation both bonds form at the same time which means this reaction is synchronous and thereby it is concerted.
LOG files
[4+2] Cycloaddition of 1,3-Dioxole and Cyclohexadiene

The endo and exo reaction pathways of this Diels Alder reaction was investigated. The product structures were built and optimised to a minimum. The two C-C bonds which formed during reaction were broken and frozen at 2.2 Å to produce guess endo and exo TS structures. These were then minimised and then optimised at B3LYP to produce the final optimised TS structures. Then IRC calculations were performed at PM6 level.
Molecular Orbital Diagrams for Endo and Exo TS

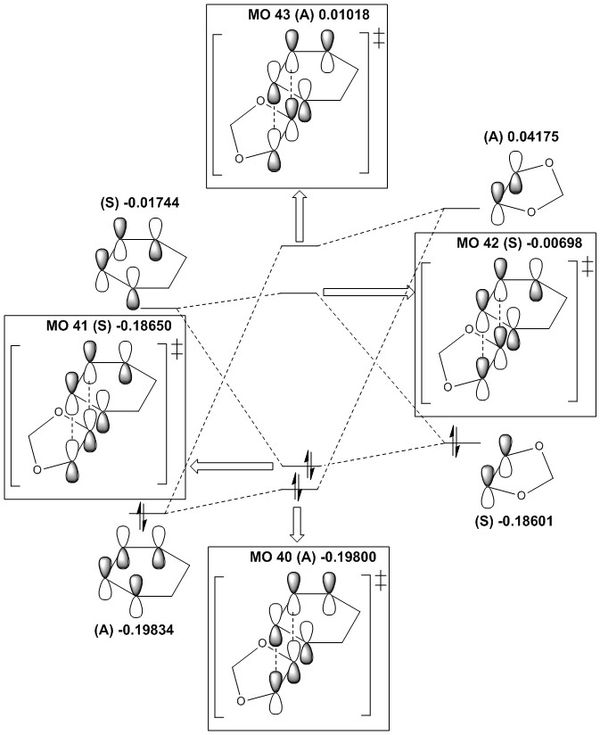
The MO diagrams are broadly similar to the MO diagram in the previous exercise where the TS MOs are higher in energy compared to reactants.In a normal electron demand process the diene HOMO is higher in energy than the dienophile HOMO, and the diene HOMO-dienophile LUMO energy gap is smaller compared to the converse dienophile HOMO-diene LUMO energy gap. However, in this reaction the HOMO of the 1,3-dioxole (dienophile) is higher in energy than the cyclohexa-1,3-diene (diene) HOMO, and this means that the reaction is an inverse electron demand Diels-Alder. This is because the dienophile is relatively electron rich as the lone pairs of electrons on oxygen can donate electron density to the C=C π-bond, thereby raising the energy of MOs above the diene. This reaction obeys the principle of conservation of orbital symmetry as well.
It is observed that the energy levels of endo and exo TS are different. The HOMO (MO41) is lower in energy in the endo TS compared to the exo TS. This is due to the secondary orbital interactions between oxygen p-orbitals and the MOs of the diene component(see below). This in turn lowers the energy of TS and the activation energy barrier of the reaction.
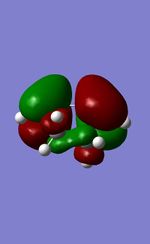
| MO | 1,3-Dioxole | Cyclohexadiene |
|---|---|---|
| HOMO |  |
|
| LUMO | 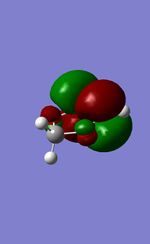 |

|
| TS | HOMO-1 | HOMO | LUMO | LUMO+1 |
|---|---|---|---|---|
| Endo |  |
 |
 |

|
| Exo |  |
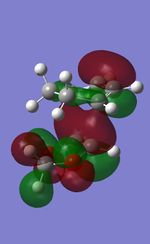 |
 |

|
Nf710 (talk) 09:30, 23 March 2018 (UTC) How do you know the electron demand of the reaction. have you investigated it properly?
Thermochemistry
| Molecule | Sum of electronic and thermal Free energies/ (Hartee/particle) |
|---|---|
| 1,3-Dioxole | -267.074708 |
| Cyclohexadiene | -233.336102 |
| Endo-TS | -500.350529 |
| Exo-TS | -500.347583 |
| Endo-Product | -500.436132 |
| Exo-Product | -500.434786 |
| Reaction Pathway | Reaction Barrier/(kJ/mol) | Reaction Energy/(kJ/mol) |
|---|---|---|
| Exo | 166.002501 | -62.9489928 |
| Endo | 158.267778 | -66.48291606 |
The thermochemistry section from the log output file contained values of the sum of electronic and thermal free energies which were used to calculate the reaction barriers and reaction energies. The values of the reaction barrier for the endo-pathway is lower than for the exo-pathway. This is due to the lower energy endo-TS which consists of stabilising secondary orbital interactions which do not exist in the exo-TS. The endo-product is comparatively lower in energy, thermodynamic product, which is shown by the more negative reaction energy. This could be explained by the presence of extra steric hindrance in the exo-product (see figure X below) and this raises the energy of the exo-product and lowers the reaction energy. Therefore it can be concluded that the endo reaction pathway provides both the kinetic and thermodynamic product. The steric repulsion between substituents in exo-pathway could increase the energy of the exo-TS as well which subsequently raises the reaction barrier energy.


Nf710 (talk) 09:32, 23 March 2018 (UTC) Good section, slightly brief but you have some good figures. Your energies are slightly out. I suspect your reactants are not fully optimized. you could have gone into more detail in areas such as the electron demand.
LOG Files
Diels Alder vs Cheletropic reactions
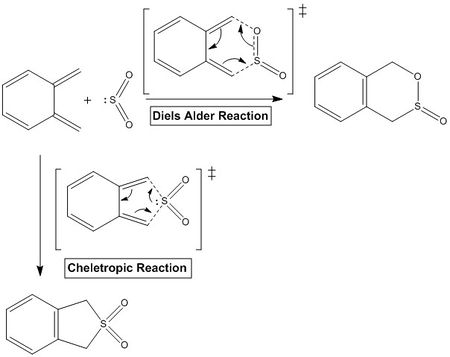
In this exercise, the possible TS produced from different reaction pathways were optimised at PM6 level. The products from each reaction were minimised and the bonds at reacting atoms were broken and frozen. Then the structures were optimised to produce an accurate TS. The LOG output files from the final optimised TS were used for the IRC calculations and to determine the free energy values for the reactants, product and TS to subsequently calculate the reaction barriers and energies for each possible pathway.
Thermochemistry
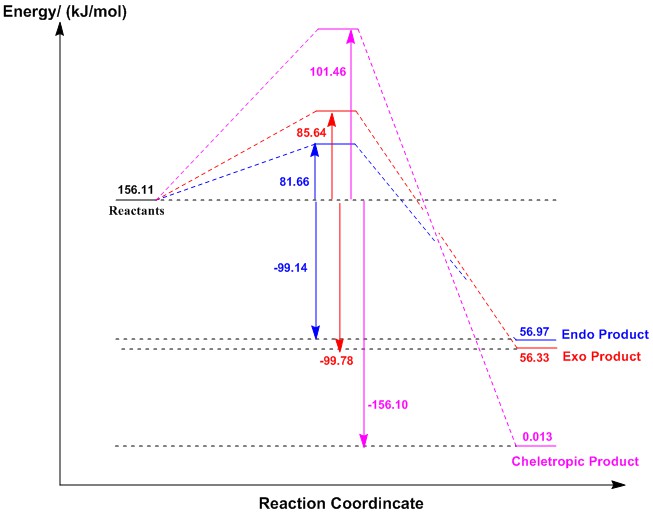
Again, the above reaction profile illustrates that the endo-product is the kinetic product due to the lowest reaction barrier. The stabilising secondary orbital interactions in the endo-TS, as seen in the previous exercise, results in a lower activation energy for the reaction. The endo-pathway has a higher reaction energy than the exo-pathway which concludes that the endo-product is more thermodynamically favoured. The cheletropic reaction pathway consists of both the largest reaction barrier and the reaction energy which means that this is the least kinetically favoured and the most thermodynamically favoured pathway. The cheletropic-product does not form from the breaking of a relatively strong S=O bonds compared to exo/endo products. The presence of two strong S=O bonds in the final product raises the reaction energy of the cheletropic-pathway. This reaction also involves the initial formation of a five-membered ring which raises the ring strain in the system compared to the chair like six-membered ring in Diels Alder chemistry. This results in an increase in reaction barrier energy and the energy of the cheletropic-TS, making it the least kinetically favourable pathway.
(You should show evidence for effects such as secondary orbital overlap Tam10 (talk) 15:48, 16 March 2018 (UTC))
| Molecule | Sum of electronic and thermal Free energies/ (Hartee/particle) |
|---|---|
| Sulfur dioxide | -0.118614 |
| o-xylylene | 0.178073 |
| Endo-TS | 0.090562 |
| Exo-TS | 0.092078 |
| Cheletropic-TS | 0.098102 |
| Endo-Product | 0.021698 |
| Exo-Product | 0.021454 |
| Cheletropic-Product | 0.000005 |
| Reaction Pathway | Reaction Barrier/(kJ/mol) | Reaction Energy/(kJ/mol) |
|---|---|---|
| Exo | 85.641191 | -99.7821351 |
| Endo | 81.6609327 | -99.14151305 |
| Cheletropic | 101.457204 | -156.0964889 |
The aromatisation of the xylylene to benzene is a major thermodynamic driving force of the reaction. This occurs in both Diels Alder chemistry and cheletropic reactions. The following animations illustrates that ortho-xylylene is highly unstable and readily converted to the aromatic product.

(It's pretty hard to tell that this is endo from this angle Tam10 (talk) 15:48, 16 March 2018 (UTC))
Reaction with alternate Butadiene component on xylylene

There is a second cis-diene unit found on xylylene which could possible undergo an alternative Diels Alder reaction with sulfur dioxide to produce exo/endo products as shown above. The same procedure was used to produce the optimised TS and the energy analysis is summarised in the tables given below.
| Molecule | Sum of electronic and thermal Free energies/ (Hartee/particle) |
|---|---|
| Sulfur dioxide | -0.118614 |
| o-xylylene | 0.178073 |
| Endo-TS | 0.095656 |
| Exo-TS | 0.093577 |
| Endo-Product | 0.065609 |
| Exo-Product | 0.067306 |
| Reaction Pathway | Reaction Barrier/(kJ/mol) | Reaction Energy/(kJ/mol) |
|---|---|---|
| Exo | 89.5768158 | 20.6023001 |
| Endo | 95.0352307 | 16.146826 |
Using the data obtained, it can be concluded that this alternate Diels-Alder pathway is both kinetically and thermodynamically unfavourable. This has a larger reaction barrier for both endo/exo TS due to the high approach trajectory for sulfur dioxide towards the sterically hindered cis-diene component within the xylylene ring compared to the exocyclic reaction pathway. The reaction energies for this pathway are both positive as it does not involve the aromatisation of the xylylene ring, raising the energy of the final product.
LOG Files
Conclusion
This study involved the use of Gaussian Software to locate the TS of three different pericyclic reactions. This information was in turn used to calculate reaction energies and reaction barrier energies.
The first reaction was a [4+2] cycloaddition between betadiene and ethene and the MOs that were involved in the reaction between the two species were investigated along with the TS. The second reaction was another [4+2] cycloaddition between 1,3-dioxole and cyclohexadiene which consisted of an inverse electron demand compared to general Diels-Alder reactions. The two different reaction pathways, exo and endo were studied and the location of the TS and the final products indicated that the endo-pathway produced both the kinetic and thermodynamic product. The final study involved the comparison between the cheletropic and Diels-Alder reaction pathways for the same reactants, Sulfur dioxide and ortho-xylylene. It was concluded that the Diels-Alder reactions for both endo and exo pathways produced the kinetic product via the lower energy TS whereas the cheletropic reaction generated the thermodynamic product with the lowest energy final product.
The experiment could be improved with the use of B3LYP method for all three reactions with better accuracy.
